Для такого построения используют признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоско­сти, то плоскости параллельны.

Задача.

Через точку D провести плоскость, параллельную плоскости, заданной пересекающимися прямыми A В и АС (рис. 92).

Решение:

Через точку D проводим прямые DE и DN , соответственно параллельные прямым AB и AC , следовательно, плоскость, заданная прямыми DK и Е K , окажется параллельной заданной плоскости. (рис. 93)

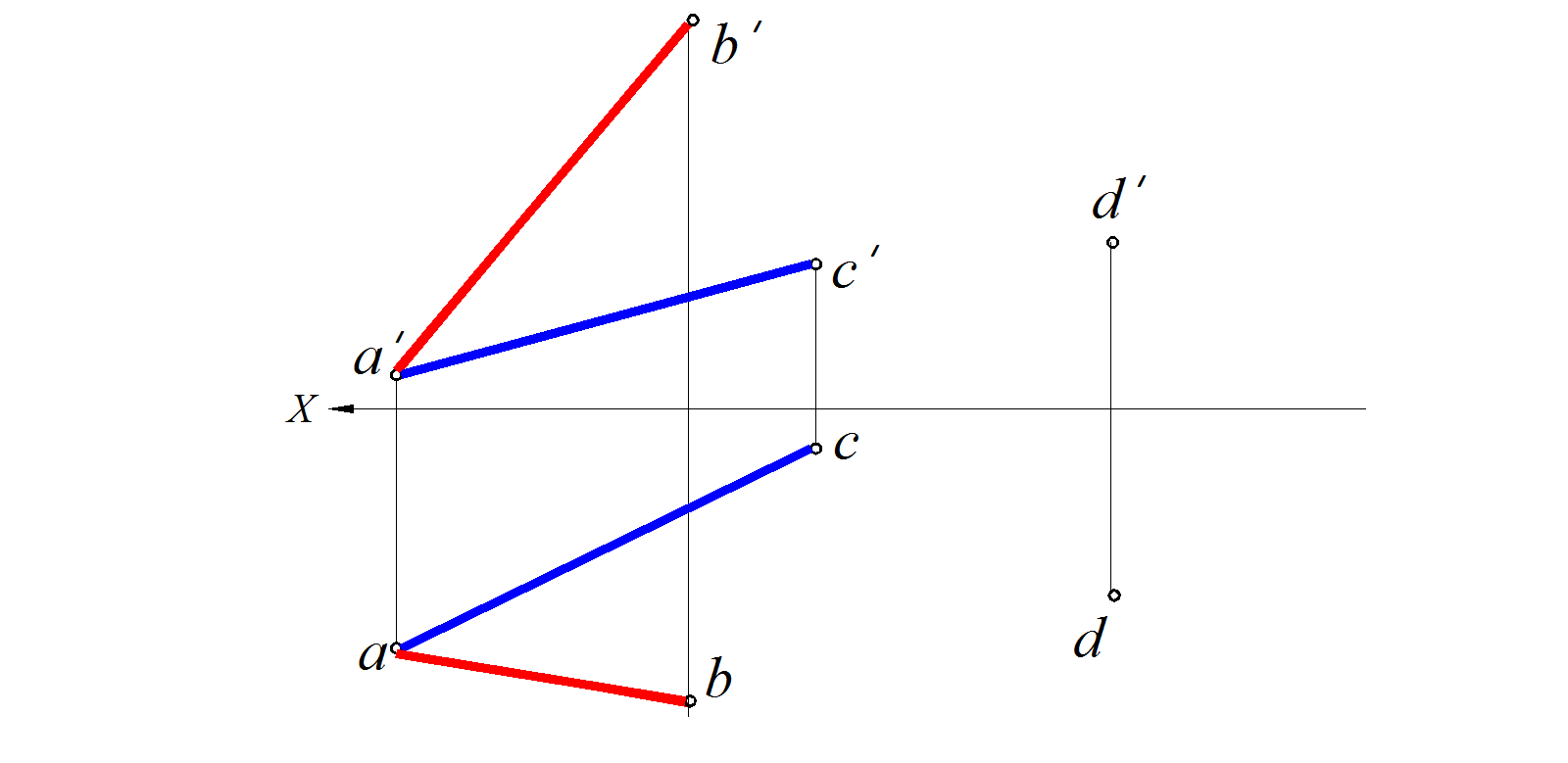
                                             Рис. 92. Условие задачи

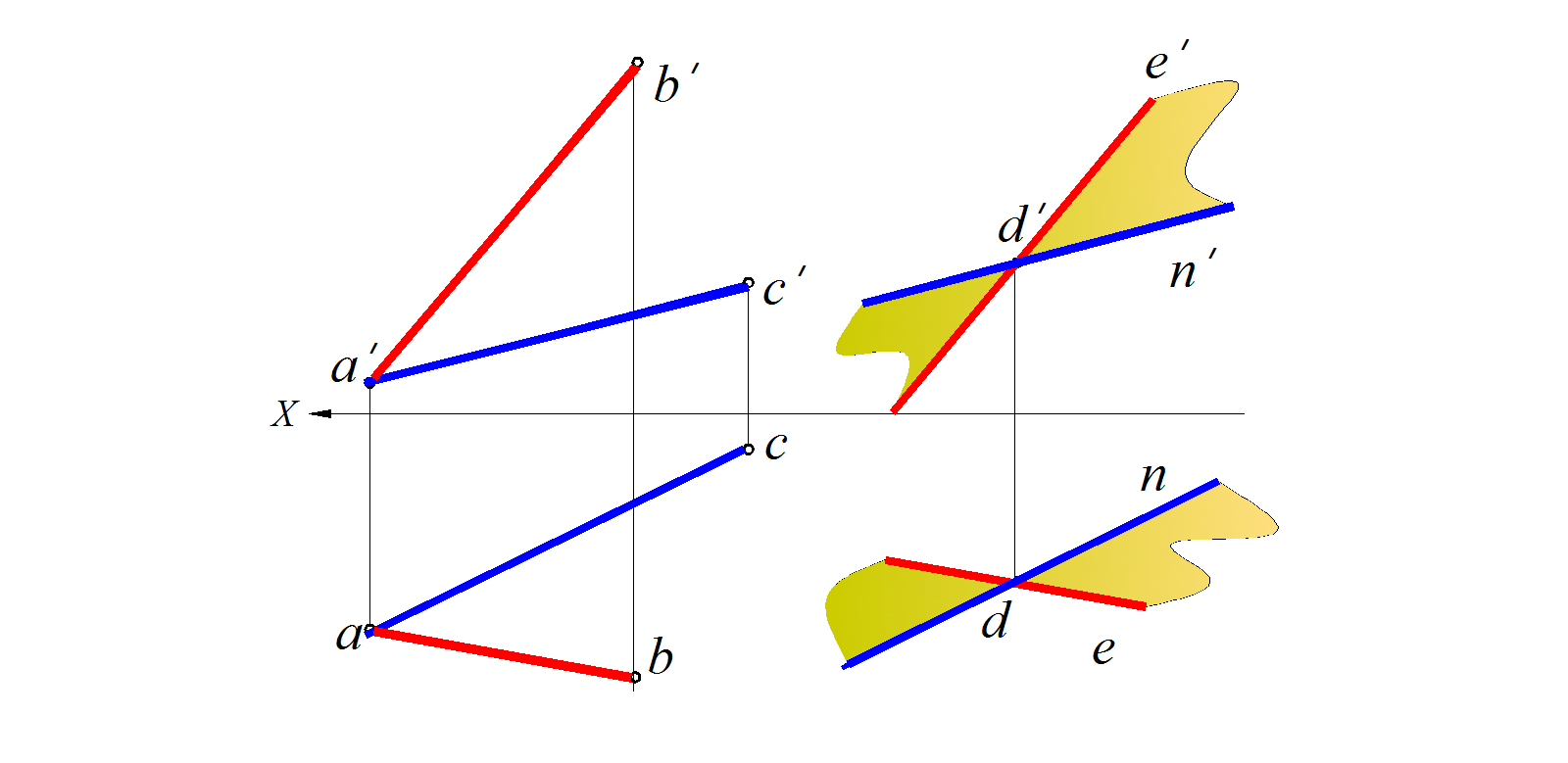
                              Рис. 93. Построение взаимно параллельных плоскостей

Задача.

Через точку А провести плоскость, параллельную плоскости Q , заданной следами (рис. 94).

      Решение:

Через точку А проведена плоскость Р параллельно заданной плоскости Q. Сначала через точку А проведена прямая AN, заведомо параллельная плоскости Р. Это горизонталь с проекциями an и a ' n ', причем an || P_H ,. Так как точка N является фронтальным следом горизонтали AN , то через эту точку пройдет след Q_V || P_V , а через Q_x – след Q_H || P_H . Плоскости Q и P взаимно параллельны, так как их одноименные пересекающиеся следы взаимно параллельны.

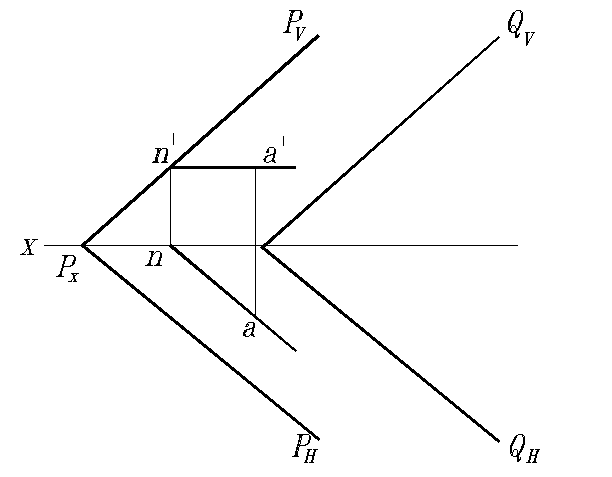
Рис. 94. Построение параллельных плоскостей, заданных следами

5. Способы преобразования чертежа

Метод замены плоскостей проекций. Метод вращения. Основные задачи, решаемые с применением способов преобразования чертежа.

Многие задачи решаются легко и просто, если прямые линии, плоские фигуры (основания, грани, ребра, оси) геометрических тел находятся в частном положении. В начертательной геометрии существует ряд методов, с помощью которых геометрические элементы общего положения переводятся в частное положение – это методы преобразования проекционного чертежа. Любое преобразование проекционного чертежа пред-ставляет собой связанную проективно цепочку геометрических образов, конечная пара в которой образует проекционную систему изображений, позволяющих с максимальной простотой реализовать решение задачи. В курсе начертательной геометрии рассматриваются, как правило, две группы методов – методы перемены плоскостей проекций и методы вращения. Рассмотрим их для преобразования чертежа прямой линии или плоской фигуры общего положения в чертеж с их частным положением.

При использовании метода перемены плоскостей проекций заданную систему плоскостей проекций заменяют на новую так, чтобы в ней исходные объекты оказались в частном положении, не меняя своего расположения в пространстве.

При методе вращения изменяют положение исходных объектов в пространстве так, чтобы они приняли частное положение относительно неизменных плоскостей проекций.

Рассмотрим более подробно указанные методы.

Все преобразования чертежа существуют для того, чтобы решение задачи стало более упрощенным. Это происходит в тех случаях, когда геометрические фигуры занимают частное положение относительно плоскостей проекций