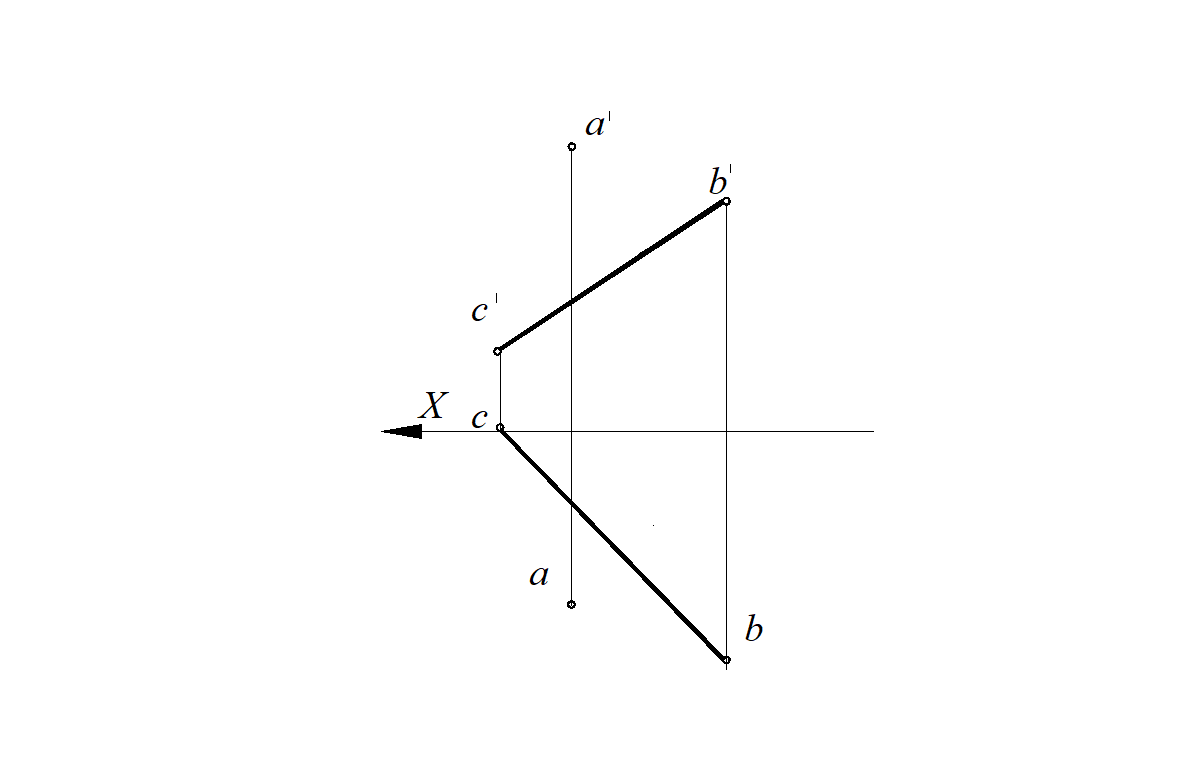
Рис. 85. Условие задачи
Решение:
1. Анализируем графическое условие задачи:
СВ - прямая общего положения
2. Зададим искомую плоскость Р пересекающимися прямыми: горизонталью Н и фронталью F: Р (H ∩ F). Тогда на основании теоремы: h ⊥ cb ; f '⊥c ' b '; P ⊥CB (рис. 86)

Рис. 86. Построение плоскости, перпендикулярной к прямой
Построение взаимно перпендикулярных плоскостей
При построении используем признак перпендикулярности двух плоскостей: две плоскости перпендикулярны, если одна из них содержит перпендикуляр к другой плоскости
Построение на эпюре возможно осуществить двумя путями:
1. Искомую плоскость проводим через прямую, перпендикулярную данной плоскости (рис. 87).
2. Искомую плоскость проводим перпендикулярно прямой, лежащей в данной плоскости (рис. 88).
Для получения единственного решения требуются дополнительные условия.
Задача.
Через данную прямую MN провести плоскость перпендикулярную данной плоскости ∆АВС. Дополнительным условием здесь служит то, что искомая плоскость должна проходить через прямую MN.
Решение:
1. Анализируем условие задачи: прямая MN общего положения и плоскость общего положения, заданная ∆АВС (рис. 87), стороны ∆АВС являются горизонталью АС и фронталью АВ.
2. Прямую MN заключаем в плоскость Р ( MN ∩ NE ). NE ⊥ ( ABC ); en⊥ac ; e ' n '⊥a ' b ' .
Построение здесь облегчено тем, что стороны ∆АВС являются горизонталью АС и фронталью АВ. В ином случае их предварительно необходимо построить.
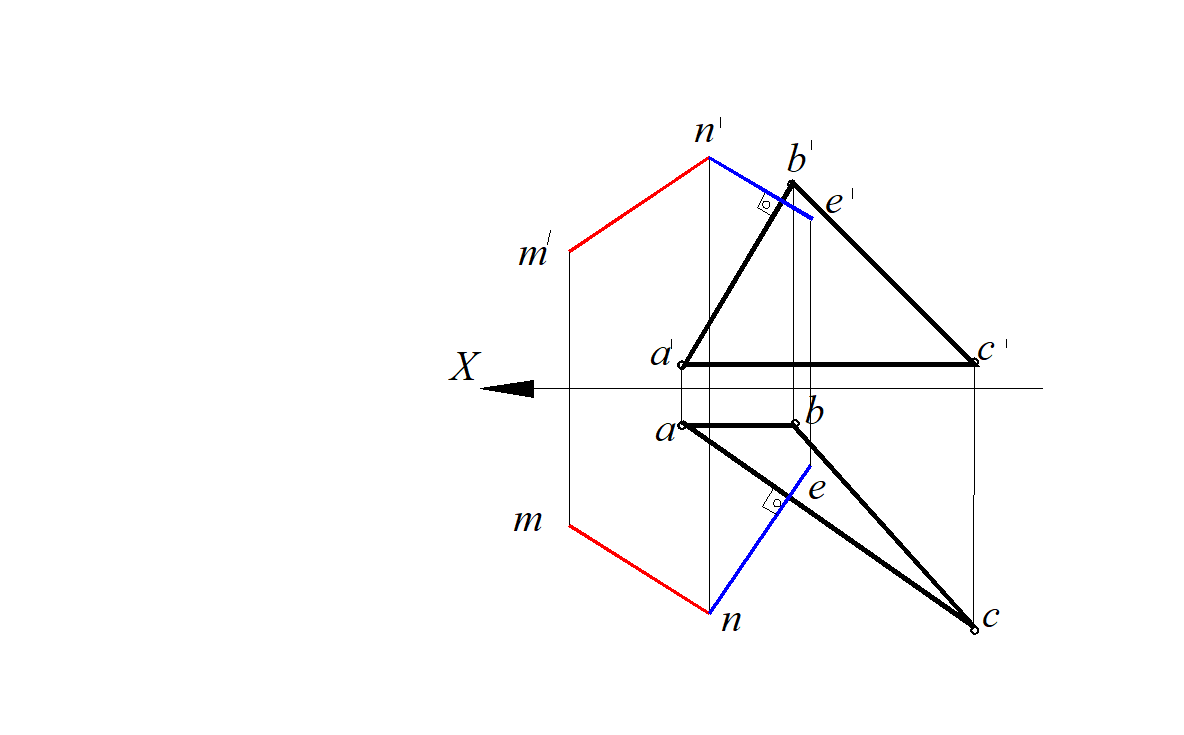
Рис. 87. Построение взаимно перпендикулярных плоскостей:
Задача.
Построить плоскость Р, перпендикулярную фронтальной плоскости проекций и плоскости, заданной ∆АВС (рис.88)
Решение:
1. Строим в плоскости ∆АВС фронталь С1. Дополнительным условием здесь является то, что искомая плоскость должна быть еще перпендикулярна плоскости проекций V .
2. Проводим плоскость Р, заданную следами, перпендикулярно фронтали треугольника. Р ⊥V ; Р v⊥c 1; Р ⊥ (АВС).
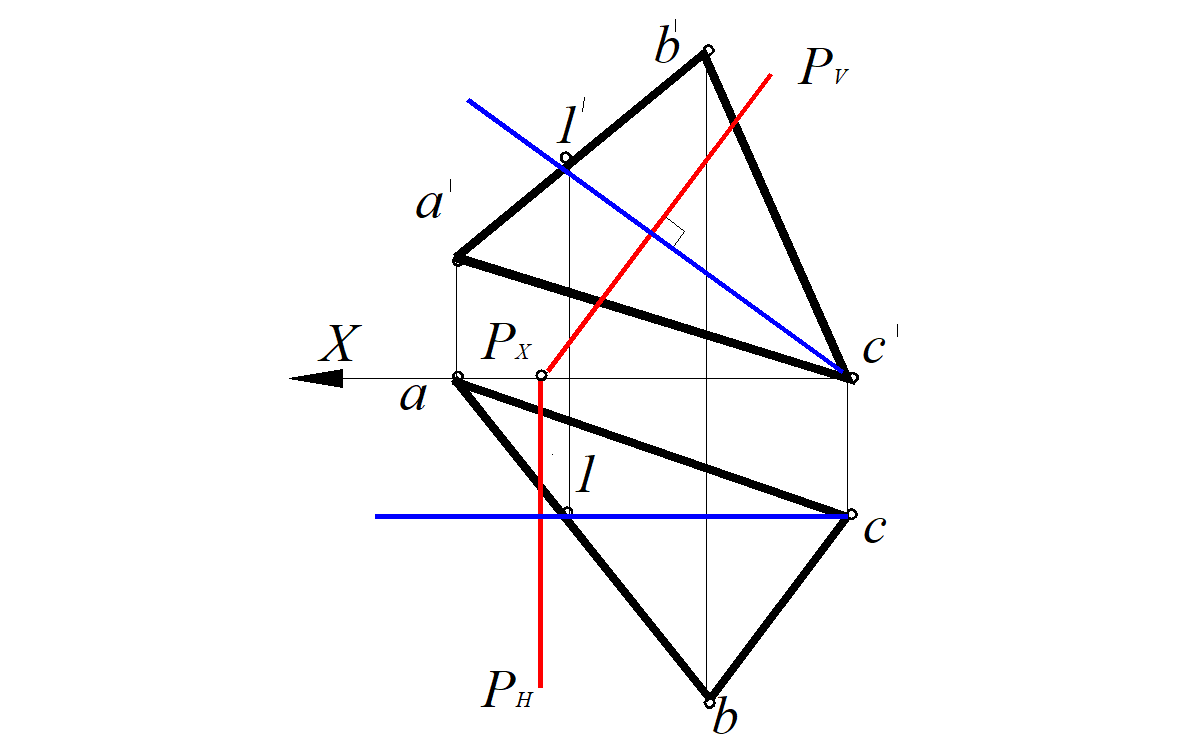
Рис. 88. Построение плоскости перпендикулярной
заданной плоскости ∆АВС и плоскости проекций V
Построение прямой линии и плоскости,
Параллельных между собой
При построении используем известный из стереометрии признак: если прямая, не принадлежащая плоскости, параллельна какой-либо прямой в этой плоскости, то она параллельна и самой плоскости.
Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие.
Задача 1. Через точку D (рис. 89, а) требуется провести прямую, параллельную плоскости, заданной треугольником ( ABC ), и плоскости проекций H (дополнительное условие).
Решение:
Очевидно, искомая прямая должна быть параллельна линии пересечения обеих плоскостей, т. е. должна быть параллельна горизонтальному следу плоскости. Горизонтальный след плоскости –это нулевая горизонталь. Горизонтали одной и той же плоскости параллельны между собой. Для определения направления этого следа можно воспользоваться горизонталью плоскости A ВС А1(h и h ′) , где через точку D проведена прямая, параллельная этой горизонтали.
а б
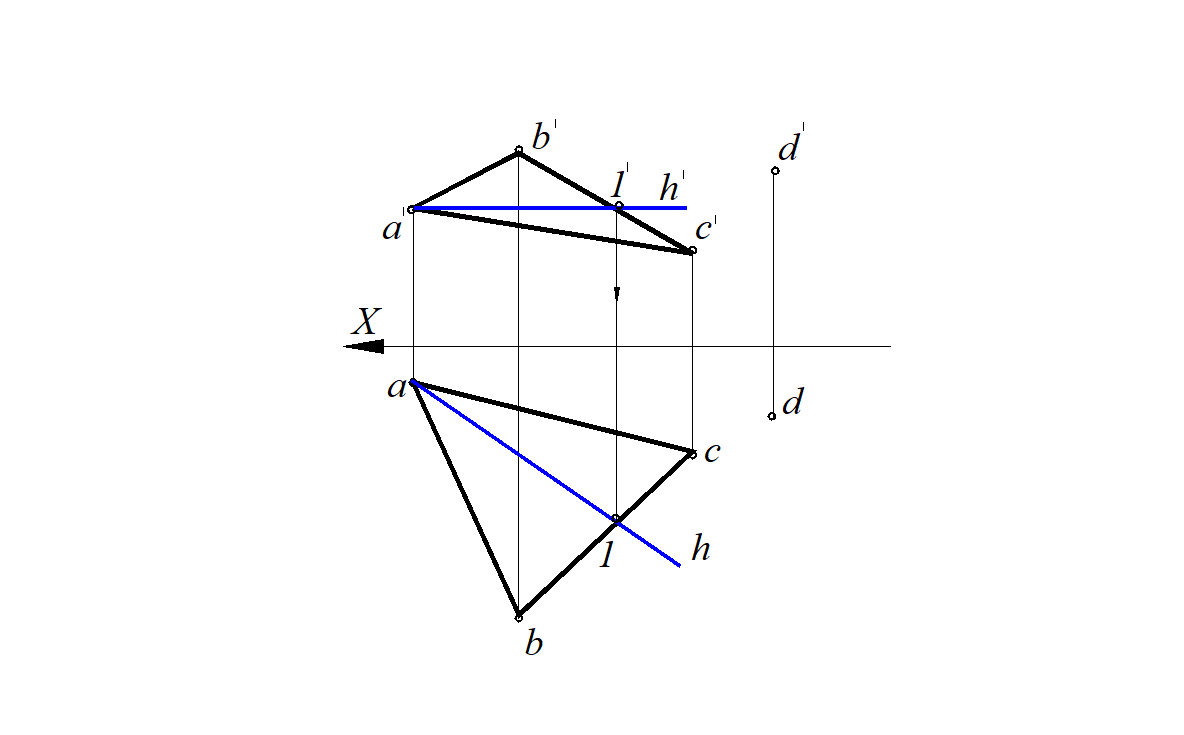
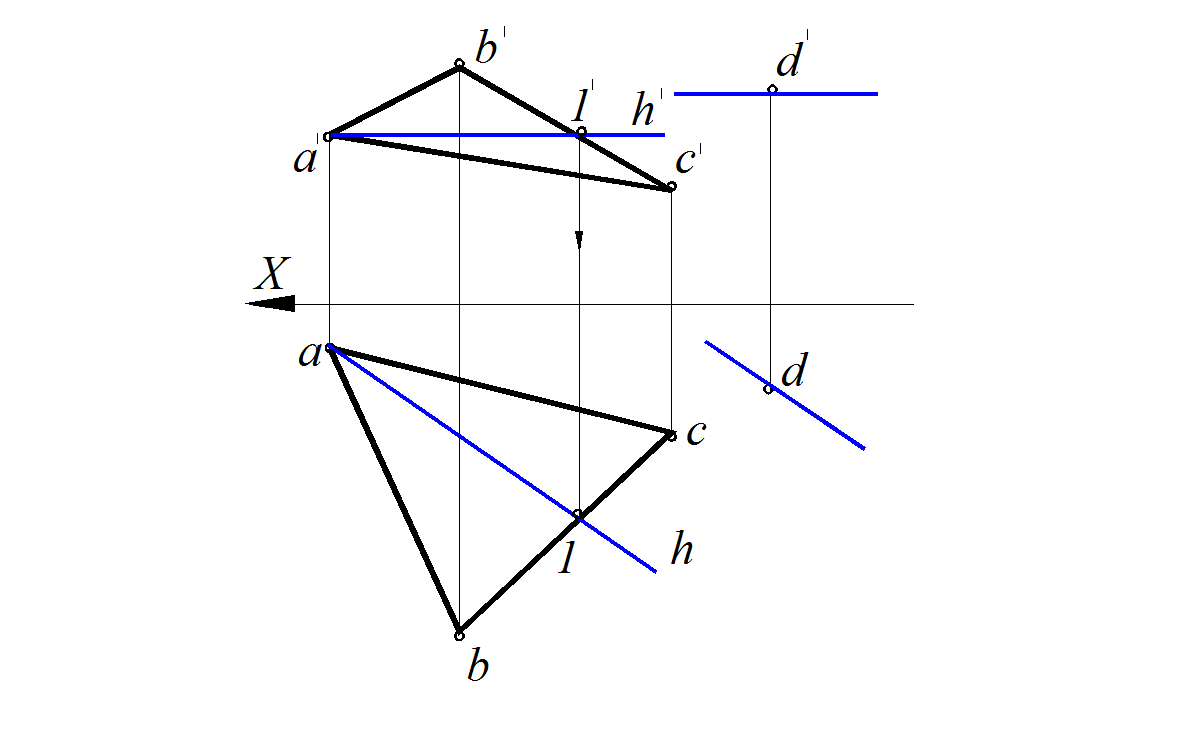
Рис. 89. Построение взаимно параллельных прямой и плоскости
а – проведение прямой параллельной плоскости Н; б – плоскости параллельной прямой
Задача 2.
Через прямую СВ провести плоскость, параллельную прямой А D (рис. 90)
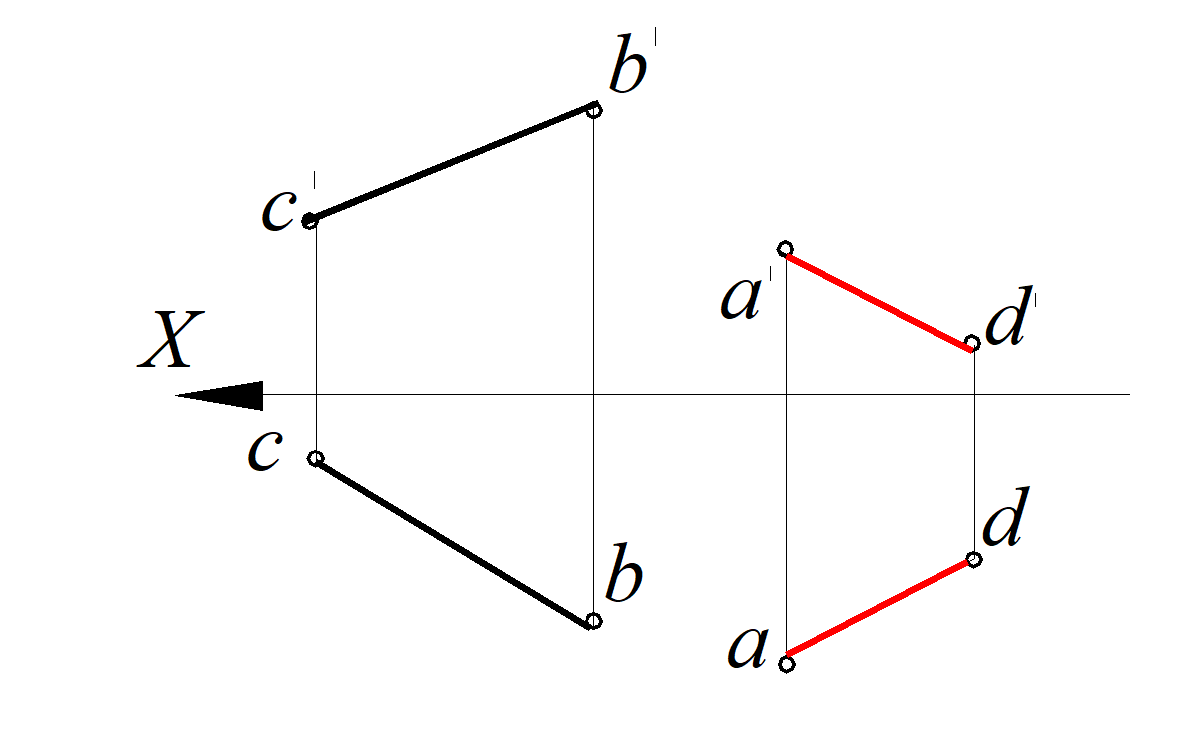
Рис. 90. Условие задачи
.
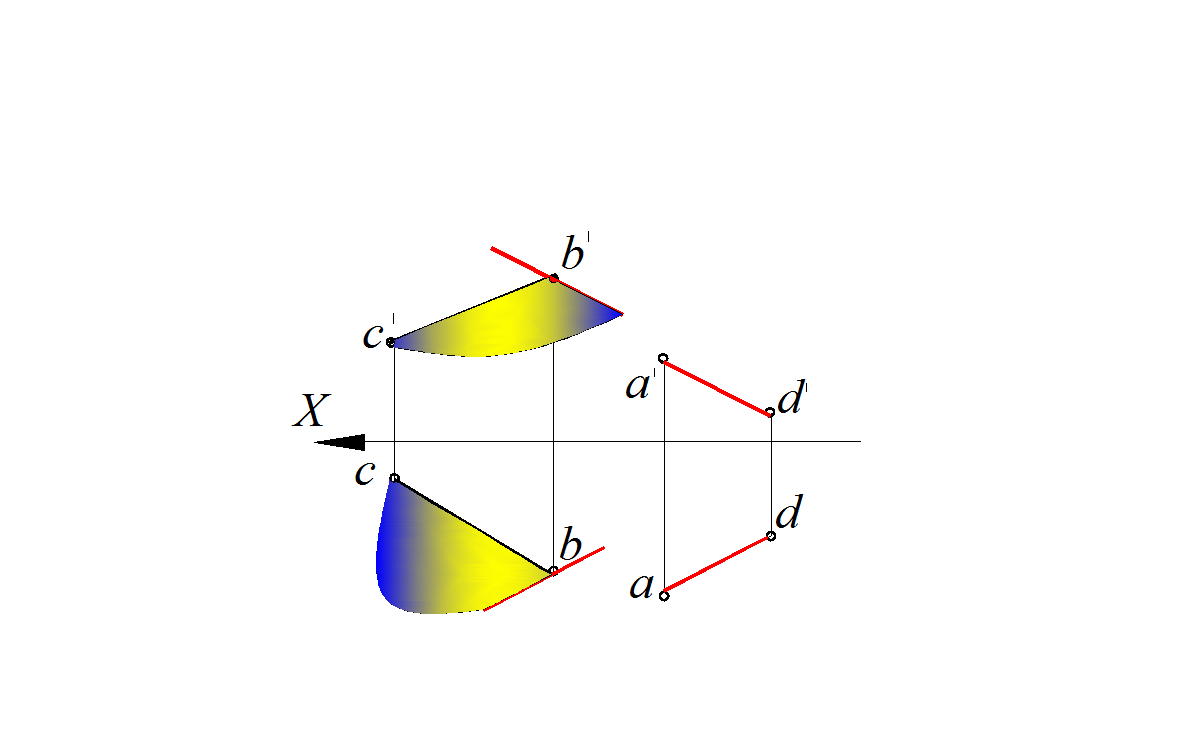
Рис. 91. Построение взаимно параллельных прямой и плоскости
плоскости параллельной прямой
Решение:
Прямые СВ и А D – скрещивающиеся. Если через одну из двух скрещивающихся прямых требуется провести плоскость, параллельную другой, то задача имеет единственное решение. Через точку В проведена прямая, параллельная прямой С D; пересекающиеся прямые АВ и BE определяют плоскость, параллельную прямой CD (рис. 91).
Дата: 2018-11-18, просмотров: 3889.