Определение

  Прямая и плоскость называются взаимно перпендикулярными, если прямая перпендикулярна каждой прямой, лежащей в этой плоскости.

                   Признаки перпендикулярности прямой и плоскости

1. Если прямая перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости, то эта прямая и плоскость взаимно перпендикулярны.

2. Через данную точку можно провести одну и только одну прямую, перпендикулярную данной плоскости.

Теоретической предпосылкой построения перпендикуляра к плоскости служит теорема о проецировании прямого угла.

Теорема о проекциях перпендикуляра к плоскости:

 Если прямая перпендикулярна заданной плоскости, то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали заданной плоскости, фронтальная проекция перпендикулярна фронтальной проекции фронтали заданной плоскости, профильная проекция перпендикулярна профильной проекции профильной прямой заданной плоскости.

Построение перпендикуляра к заданной плоскости рассмотрим на примере:

Задача.

Из точки C восстановить перпендикуляр – прямую М к плоскости ∆ ABC. (рис. 81,а)

Прямая, перпендикулярная плоскости, перпендикулярна любой прямой этой плоскости. Следовательно, по теореме, она перпендикулярна горизонтали и фронтали этой же плоскости.

Решение:

1. Проведем в заданной плоскости общего положения ∆АВС горизонталь CD (рис. 81, б).

2. Согласно теореме проведенная прямая должна соответствовать условию: М⊥С D , На чертеже прямая М проводится: m⊥cd ; (рис. 82, а).

  3. Проведем в заданной плоскости общего положения ∆АВС фронталь АЕ (рис. 82, б).

4. Согласно теореме проведенная прямая должна соответствовать M⊥АЕ . На чертеже прямая М проводится: m ' ⊥a ' e '.

5. Следовательно, из точки с проводим прямую на горизонтальной проекции m⊥cd   и на фронтальной проекции из точки с′– прямую m ' ⊥a ' e ' (рис. 83).

                                          а                                                    б

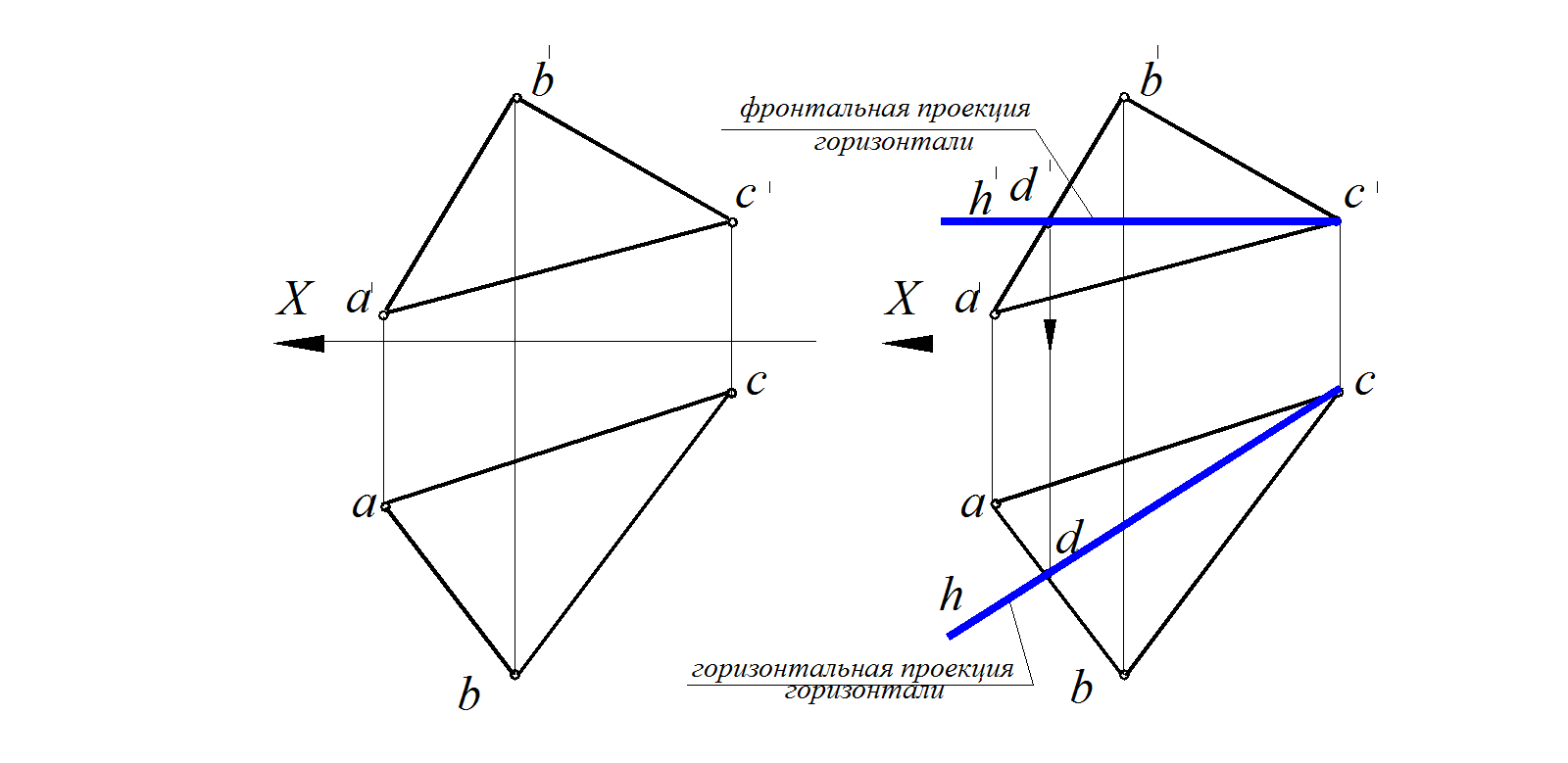
Рис. 81. Построение перпендикуляра к плоскости общего положения:

   а – условие задачи               б– построение горизонтали в плоскости ∆АВС

                а                                                                                                  б                                 

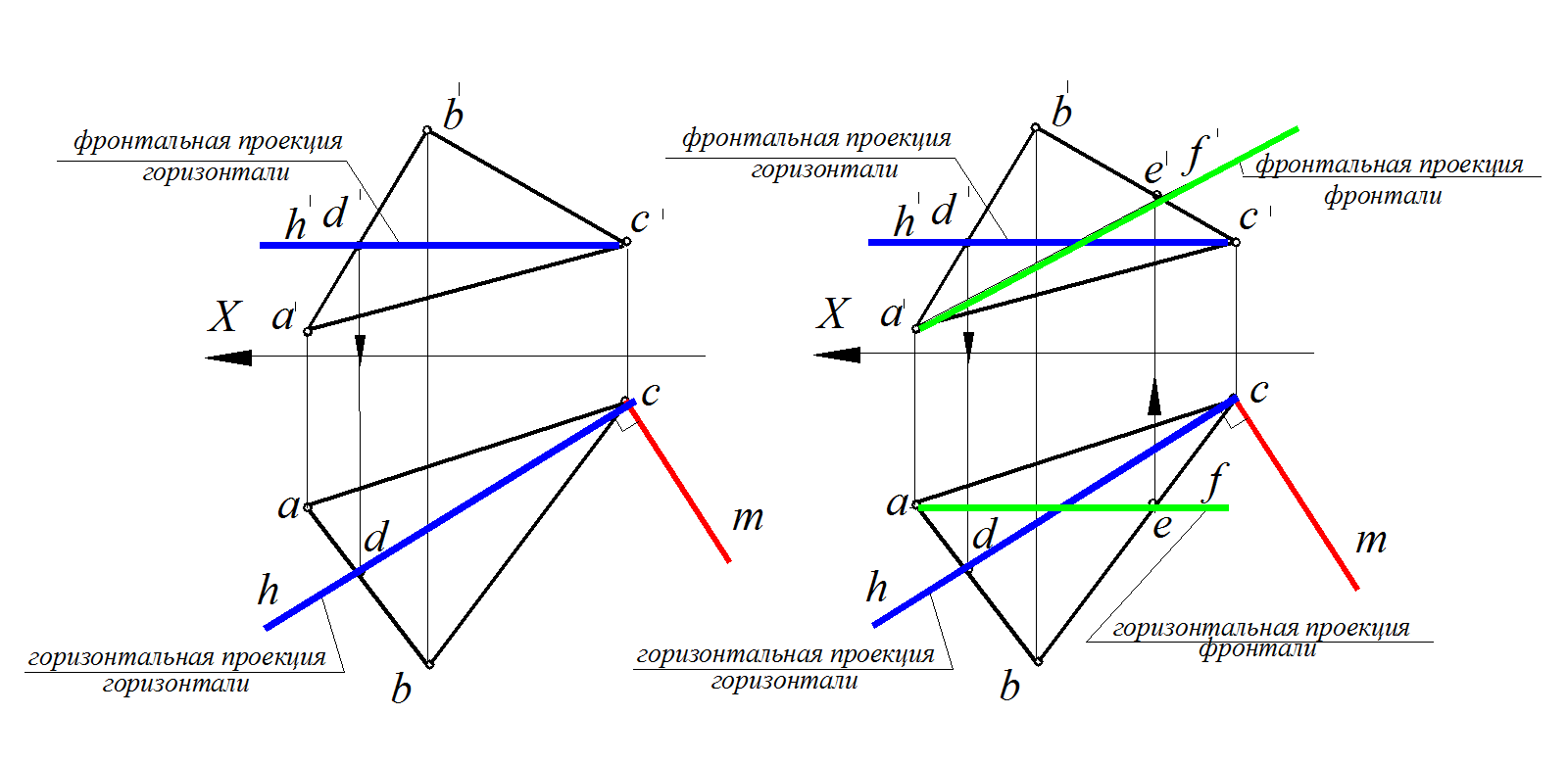
Рис.82. Построение перпендикуляра к плоскости общего положения:

 а –построение горизонтальной проекции перпендикуляра  

 б– построение фронтали в плоскости ∆АВС

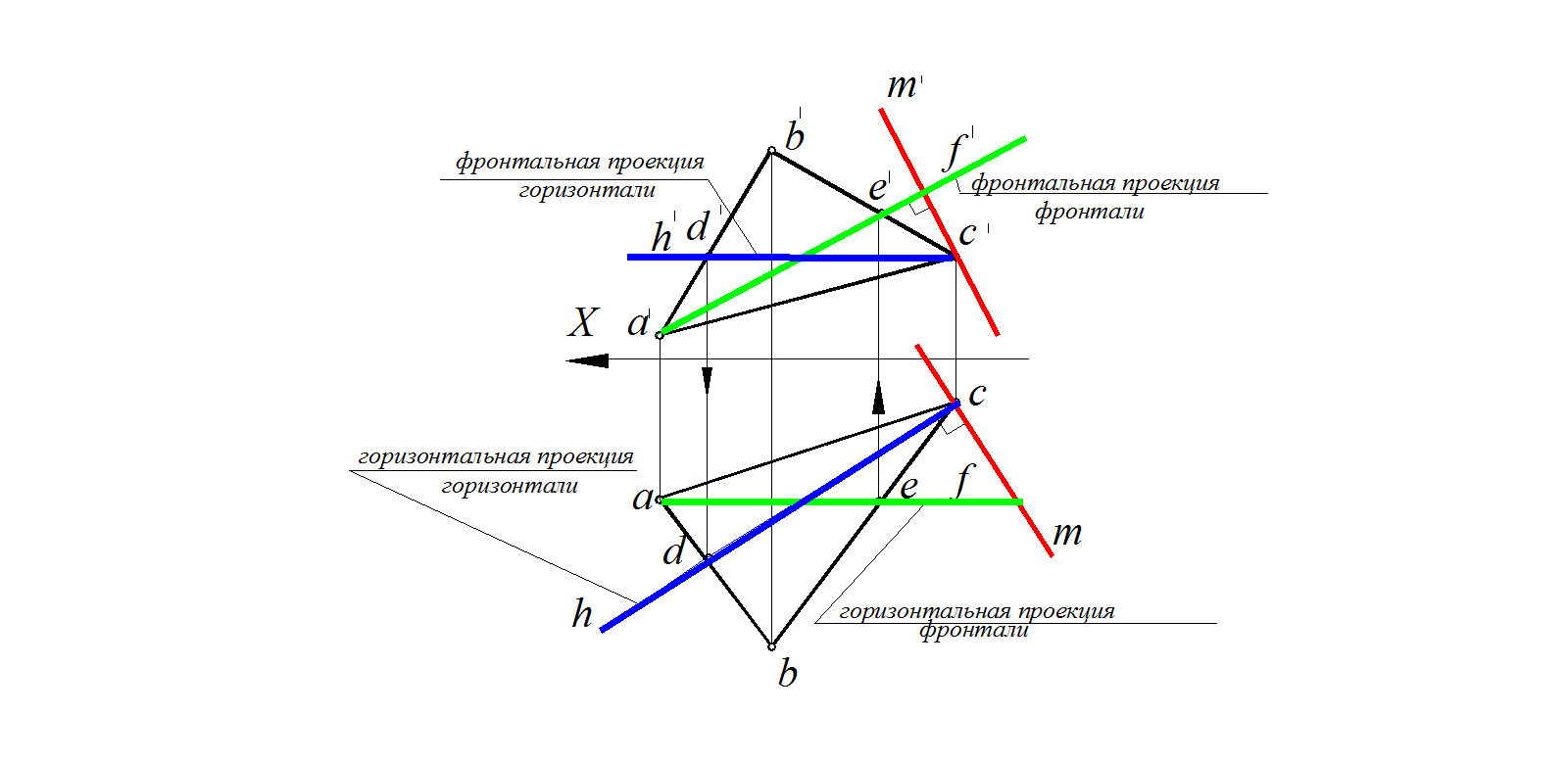
Рис. 83. Построение перпендикуляра к плоскости общего положения

Если плоскость задана следами (рис. 84), мы получаем следующий вывод: если прямая перпендикулярна к плоскости, то ее горизонтальная проекция перпендикулярна горизонтальному следу плоскости (нулевой горизонтали), фронтальная проекция перпендикулярна фронтальному следу плоскости (нулевой фронтали). На рис. 84 через точку В проведена прямая, перпендикулярная плоскости Р, заданной на чертеже следами.

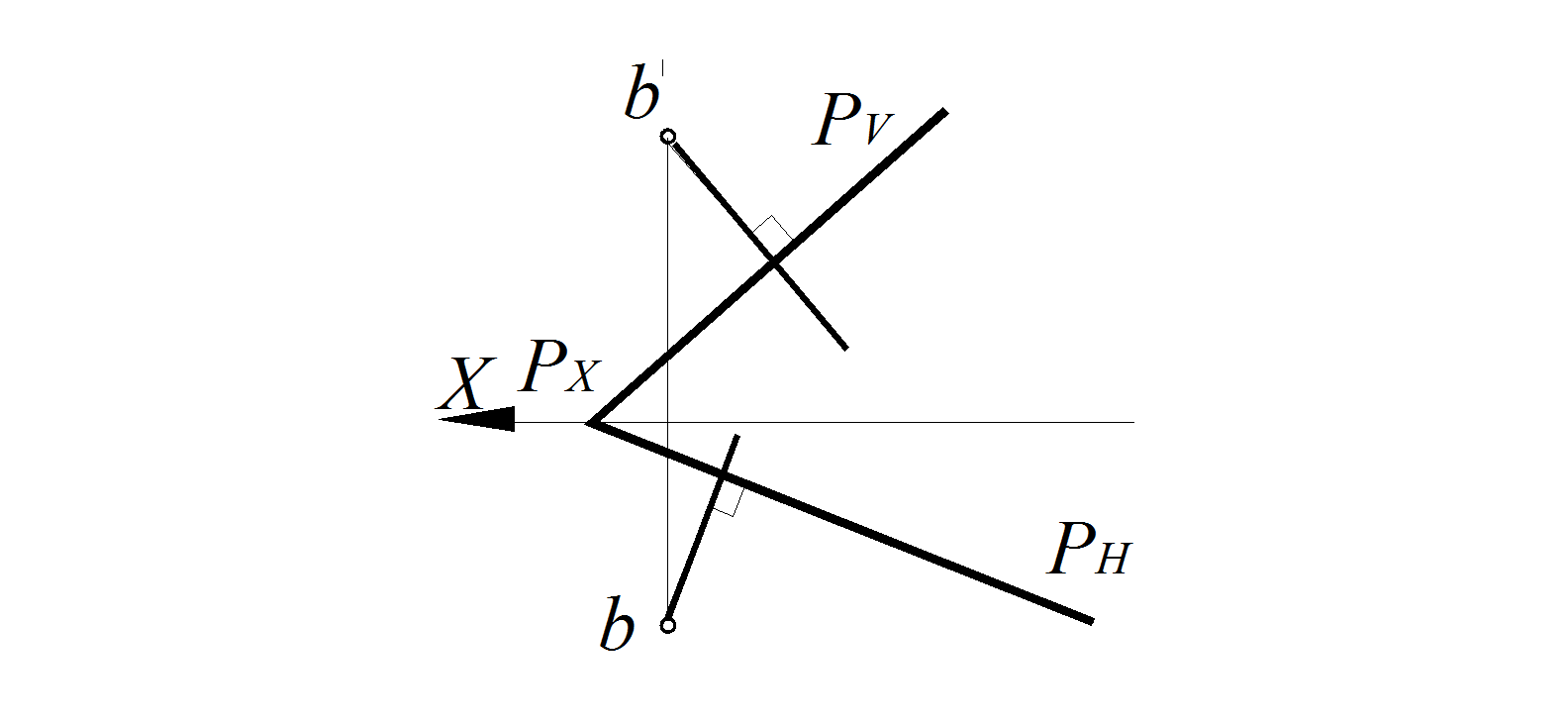
Рис. 84. Прямая, перпендикулярная плоскости Р, заданной следами

Применяя эту теорему можно легко решить обратную задачу – построить плоскость, перпендикулярную заданной прямой (рис. 85).

Задача.