Задача.
Построить точку пересечения прямой общего положения с плоскостью общего положения. Определить видимость прямой относительно плоскости
Рассмотрим на примере построения точки пересечения прямой общего положения DE с плоскостью общего положения, заданной ∆АВС (рис. 71, а).
Решение:
1. Через данную прямую проводят вспомогательную плоскость (обычно это плоскость частного положения). В нашей задаче проводим фронтально проецирующую плоскость Р (рис. 71, б):

2. Строят линию пересечения заданной и вспомогательной плоскостей: (рис. 72, а).
∆ ABC ∩ P =(1–2); а' c ' ∩ PV = 1'; а' b ' ∩ PV = 2'; I∈ АС; II∈ АВ.
3. Определяем искомую точку пересечения прямой и плоскости как точку пересечения Е в пересечении построенной линии (1-2) с заданной прямой MN :
1-2 ∩ m n = e; (рис. 72, б).
4. Определяем видимость заданной прямой MN относительно заданной плоскости ∆ ABC (рис73, а, б).
Для определения видимых участков прямой М N анализируют положение точек на скрещивающихся прямых.
Невидимый участок на горизонтальной проекции прямой E М выявляют анализом положения точек с проекциями 5', 5 и 4', 4, лежащих на скрещивающихся прямых BC и DE с проекциями b 'с', bc и d ' e ', de . По фронтальной проекции очевидно, что если смотреть по стрелке К, то вначале видят точку 5, расположенную выше точки 4. Она закрывает точку 4. Следовательно, в этом месте прямая М E закрыта ∆ ABC до точки их пересечения М (участок с проекцией т-5). Слева от точки пересечения Е прямая М N находится над ∆ ABC и, естественно, видима (участок с проекцией е m ). (рис. 73, а)
Невидимый участок на фронтальной проекции прямой E М выявляют анализом положения точек с проекциями 3', 3 и 2', 2 , которые находятся на скрещивающихся прямых DE и AB с проекциями d ' e ', de и a ' b ', ab соответственно. Их фронтальные проекции 2' и 3' совпадают. По горизонтальной проекции при взгляде по стрелке N видно, что точка 3 находится перед точкой 2, т. е. она закрывает точку 2. Следовательно, прямая DE слева от точки E расположена перед треугольником (ABC). Поэтому фронтальная проекция d ' m ' ее показана как видимая. От точки М вправо прямую DE закрывает ∆ ABC до точки 1, соответственно отрезок т'1' показан как невидимый. (рис. 73, б)
а б
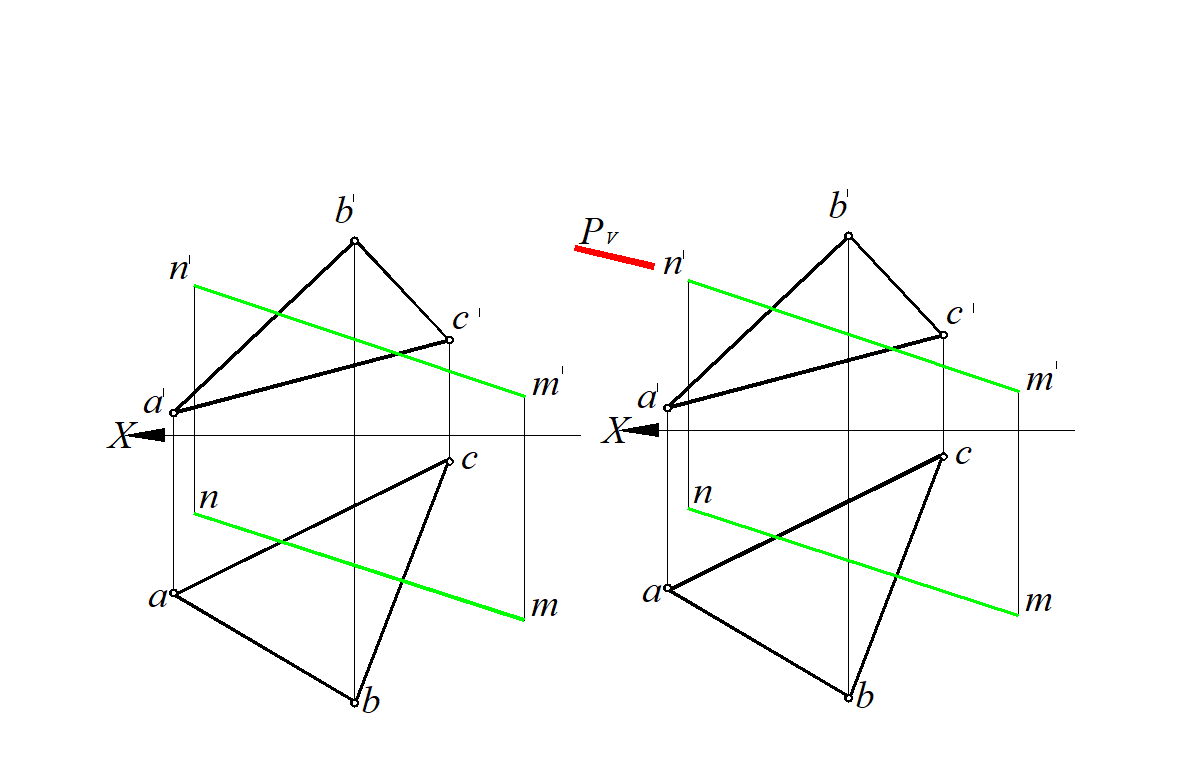
Рис. 71. Построение линии пересечения плоскости общего положения ∆АВС
с отрезком MN прямой линии общего положения:
а – условие задачи; б – через прямую проводят плоскость Р
а б
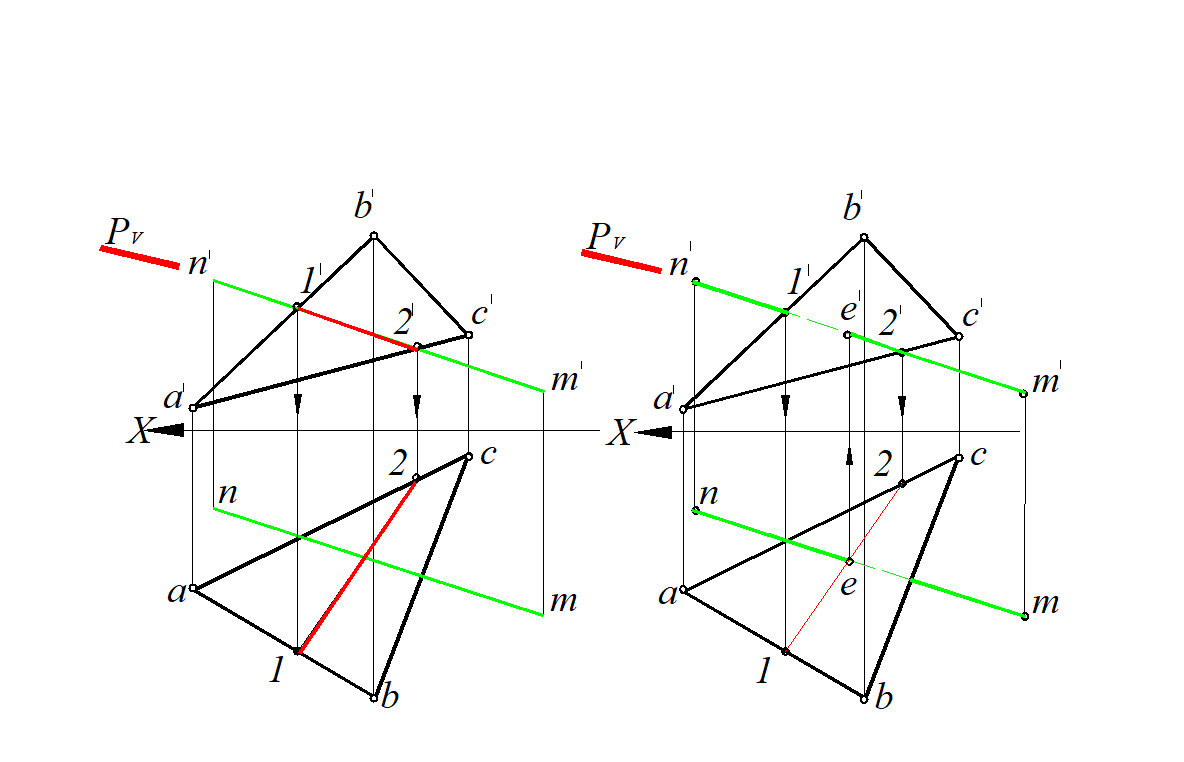
Рис. 72. Построение линии пересечения плоскости общего положения ∆АВС
с отрезком MN прямой линии общего положения:
а – построение линии пересечения б – построение точки пересечения Е
плоскости Р с плоскостью ∆АВС прямой MN c плоскостью ∆АВС
а б

Рис. 73. Построение линии пересечения плоскости общего положения ∆АВС
с отрезком MN прямой линии общего положения:
а – определение видимости прямой М N б – определение видимости прямой М N на плоскости Н на плоскости V
Дата: 2018-11-18, просмотров: 1194.