Двух плоскостей

Прямая линия, не лежащая в плоскости, может иметь с ней только одну точку. Если эта точка собственная, то прямая и плоскость пересекаются, если несобственная, то – параллельны.

То же касается и взаимного положения двух плоскостей. Две плоскости пересекаются по прямой линии. Если эта прямая собственная, то плоскости пересекаются, если несобственная – параллельны, т. е. плоскости не имеют общих точек.

Рассмотрим сначала позиционные задачи на пересечение прямой и плоскости; двух плоскостей. Две из этих задач носят название вспомогательные, две другие – основные. Вспомогательными некоторые задачи называют потому, что по условию плоскость занимает в них частное положение.

Решив такие задачи, можно перейти к решению основных задач, где геометрические объекты занимают общее положение.

Вспомогательные (простейшие) позиционные задачи

Пересечение прямой общего положения с проецирующей плоскостью

Пример построения точки пересечения прямой общего положения АВ c фронтально-проецирующей плоскостью, заданной треугольником СМ N показан на рис.68, а.

                                    а                                             б

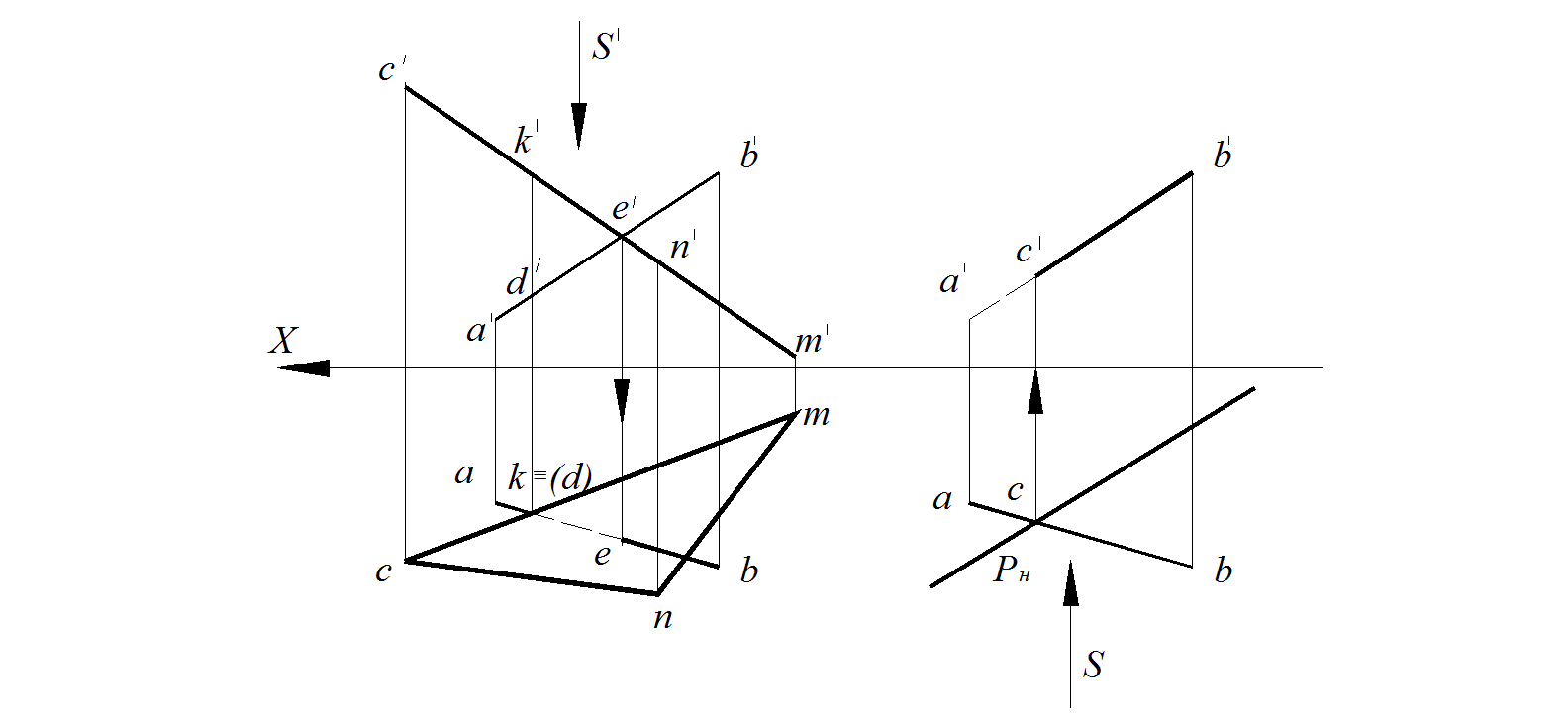
Рис. 68. Построение точки пересечения прямой

с проецирующей плоскостью, заданной:

а –∆СМ N ; б – следами плоскости Р

S–направление взгляда при определении видимости объектов

Решение в данном случае простое. Точку пересечения нужно только отметить, т. к. любая точка, принадлежащая проецирующей плоскости, будет проецироваться на соответствующий след такой плоскости. Поэтому определяем сначала фронтальную проекцию искомой точки е', а потом по свойству принадлежности точки прямой отмечаем горизонтальную проекцию е

АВ∩ ∆ CMN = Е; а′ b ′∩ ∆ n ′т′ c ′= e ′; E m ' 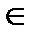e ' f '

Левее от точки Е плоскость треугольника СМ N при взгляде сверху закрывает отрезок прямой, т. е. на фронтальной проекции левее точки е прямая невидима до границы проекции а'с' плоскости треугольника.

Другой пример построения точки пересечения прямой общего положения АВ с горизонтально проецирующей плоскостью Р, заданной следами, приведен на рис. 68, б. горизонтальная проекция с точки пересечения является точкой пересечения фронтального следа Р_н и горизонтальной проекции a ' b ' прямой. Фронтальную проекцию с находят на фронтальной проекции ab прямой по свойству принадлежности:

AB ∩ P = K ; a ' b '  ∩ P _V = k ';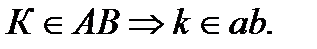

Слева от точки С прямая АВ закрыта плоскостью Р, поэтому на фронтальной проекции слева от точки С проекция а' b ' невидима.

Пересечение плоскости общего положения с проецирующей

Плоскостью

В этом случае построение линии пересечения упрощается тем, что одна ее проекция совпадает с проекцией проецирующей плоскости на ту плоскость проекций, к которой она перпендикулярна.

В качестве примера на рис. 69 показано построение проекций e ' d ', ed линии пересечения ED фронтально-проецирующей плоскости Р с плоскостью треугольника АВС:

ED = ( ABC ) ∩ P .

На фронтальной проекции в пересечении проекций а' b ' и а'с' со следом P_v находим фронтальные проекции e ' и d ' двух общих точек заданных плоскостей:

а' b ' ∩ P_v = e '; а'с' ∩ P_v = d '.

По ним построены горизонтальные проекции e и d на горизонтальных проекциях ab и ас сторон треугольника. Через точки e и d проводим горизонтальную проекцию линии пересечения плоскостей.

При взгляде по стрелке S по фронтальной проекции очевидно, что часть треугольника левее линии пересечения Е D ( e ' d ') находится над плоскостью Р, т. е. видима, остальная часть – под плоскостью Р, т. е. невидима (участок ade показан штриховой линией).

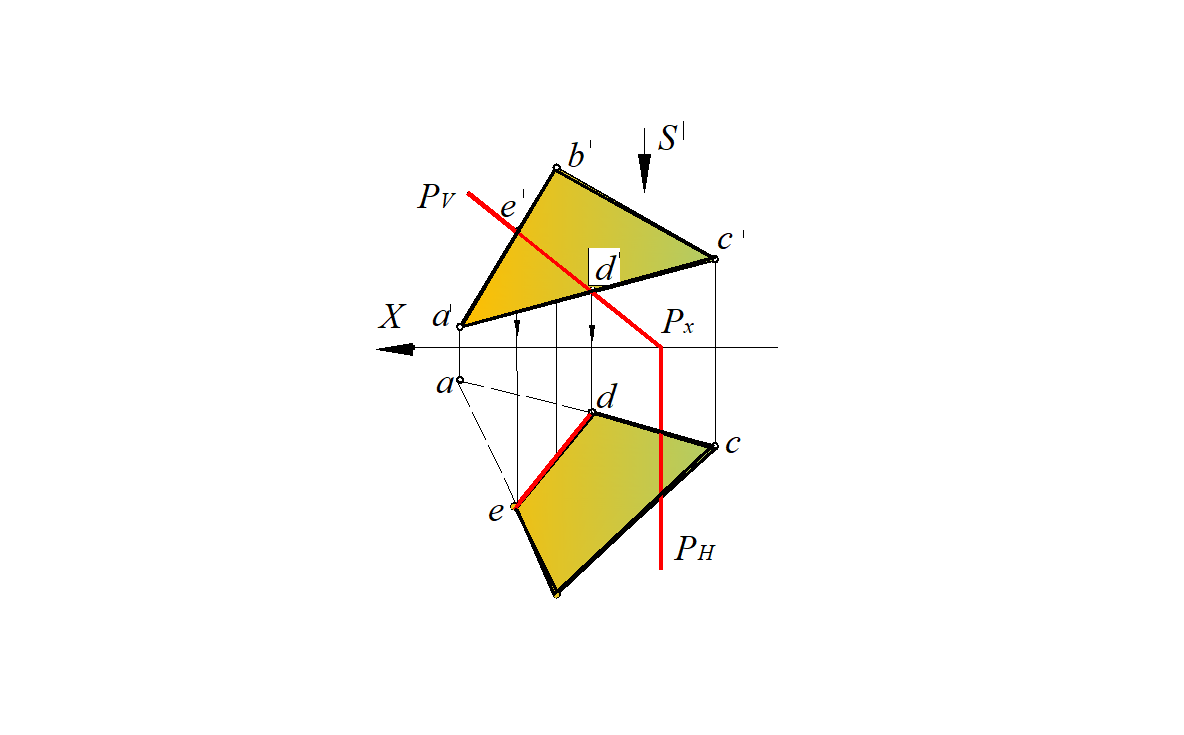
Рис. 69. Построение линии пересечения плоскости общего положения АВС

с проецирующей плоскостью Р, заданной следами

S–направление взгляда при определении видимости объектов

Другой пример построения линии пересечения двух тре­угольников (ABC) и (DEF), один из которых (DEF) задан как горизонтально-проецирующая плоскость, приведен на рис.3.MN = ( ABC ) ∩ ( DEF ).

На горизонтальной проекции в пересечении гори­зонтальных проекций ab и be сторон ∆АВС с проекцией ( dfe ) вто­рого треугольника находим горизонтальные проекции m и n точек их пересечения:

ab ∩ (dfe) = m; be ∩ (dfe) = n.

По ним на фронтальных проекциях сторон а' b ' и b 'с' строим фронтальные проекции т' и п' точек линии пересечения MN .

На фронтальной проекции отмечаем видимость частей треугольников, руководствуясь следующим: при взгляде по стрелке S по горизонтальной проекции очевидно, что сторона АС находится перед плоскостью треугольника (DEF).

Следовательно, сторона АС и ограничиваемая ею часть треугольника (A ВС) до линии пересечения MN видимы (т. е. видима фронтальная проекция четырехугольника а'с'п'т'). Видимая часть фронтальной проекции ∆DEF на чертеже оттенена.

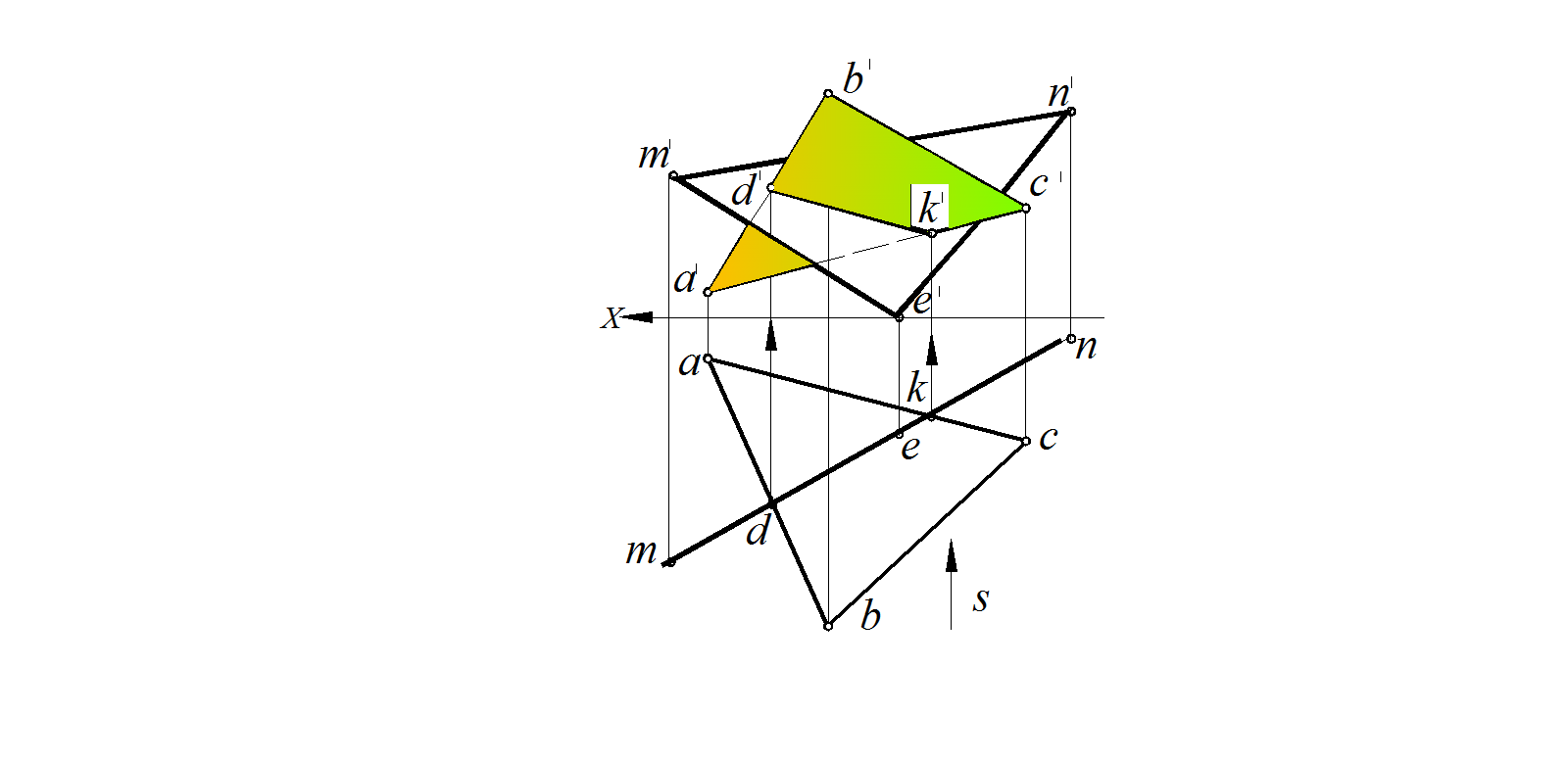
Рис. 70. Построение линии пересечения плоскости общего положения ∆АВС

с проецирующей плоскостью, заданной ∆MNE

S–направление взгляда при определении видимости объектов

Основные позиционные задачи