Линиями наибольшего наклона плоскости к плоскостям проекций V и Н называются прямые, лежащие в данной плоскости и перпендикулярные соответственно к фронтали или горизонтали данной плоскости.

Линии наибольшего наклона можно также проводить перпендикулярно следам плоскости, т. к. фронталь плоскости параллельна фронтальному следу («нулевой» фронтали), горизонталь плоскости параллельна горизонтальному следу («нулевой» горизонтали) (рис. 65).

AB – линия наибольшего наклона (ската) к плоскости Н.

AC – линия наибольшего наклона к плоскости V.

∠α – угол наклона плоскости Р к плоскости проекций Н = α°.

∠β – угол наклона плоскости Р к плоскости проекций V = β°.

Рассмотрим на конкретных примерах способы определения углов наклона заданной плоскости к плоскостям проекций V и H.

Определение углов наклона заданной плоскости к плоскостям проекций V и H

 способом прямоугольного треугольника

Задача 1.

 Определить угол наклона плоскости Р(А DE ) к плоскости проекций Н. (рис. 66)

Решение:

1. В плоскости Р провести горизонталь Н ( h ', h).

2. Из вершины А, перпендикулярно горизонтали, построить отрезок АВ – линию ската, лежащую в этой плоскости; построение линии ската начинается с горизонтальной проекции при условии, что |ab| ⊥ h .

3. Определить действительную величину отрезка АВ методом прямоугольного треугольника, одним катетом которого будет горизонтальная проекция этого отрезка |ab|.

4. Искомым углом α является угол между гипотенузой |а_о b| треугольника (aba_o) и горизонтальной проекцией линии ската ab.

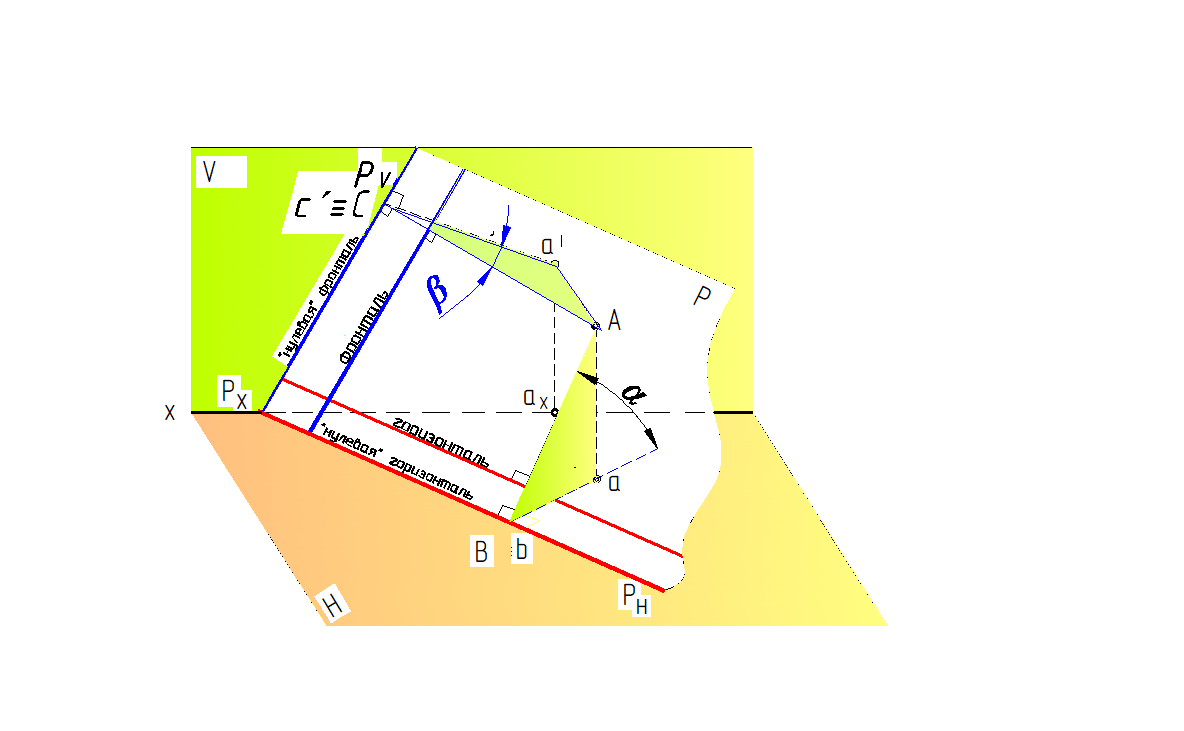
Рис. 65. Пространственная модель линий наибольшего наклона плоскости

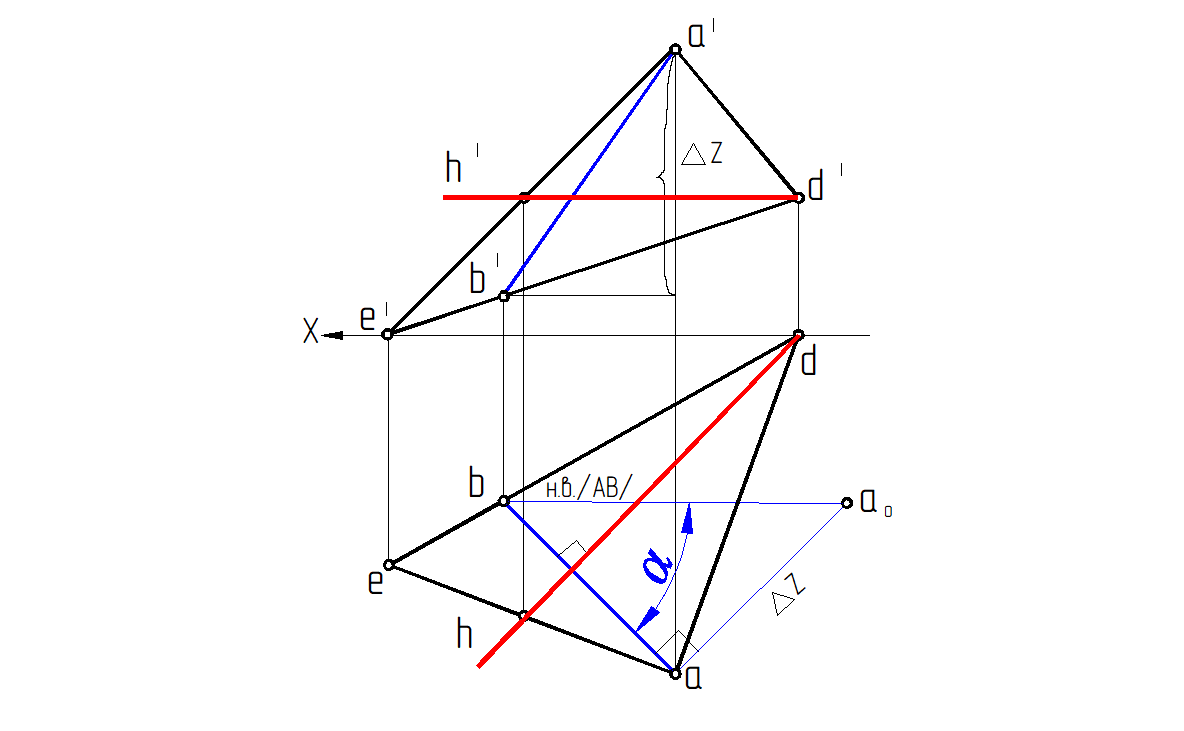
Рис. 66. Определение ∠α плоскости ∆АЕ D по линии ската

Задача 2.

 Определить угол наклона плоскости Р к плоскости проекций V . (рис. 67)

     Решение:

1. В плоскости Р провести фронталь F ( f ′, f ).

2. Из вершины А перпендикулярно фронтали, провести отрезок |АС| – линию наибольшего наклона, лежащую в этой плоскости, построение линии наибольшего наклона начинается с построения фронтальной проекции при условии, что a ′ c ′ ⊥ f ′.

3. Определить натуральную величину отрезка [АС] методом прямоугольного треугольника, одним катетом которого является его фронтальная проекция.

4. Искомым углом β является угол между гипотенузой а_ос′ треугольника a ′ c ′ a_o и фронтальной проекцией a ′ c′.

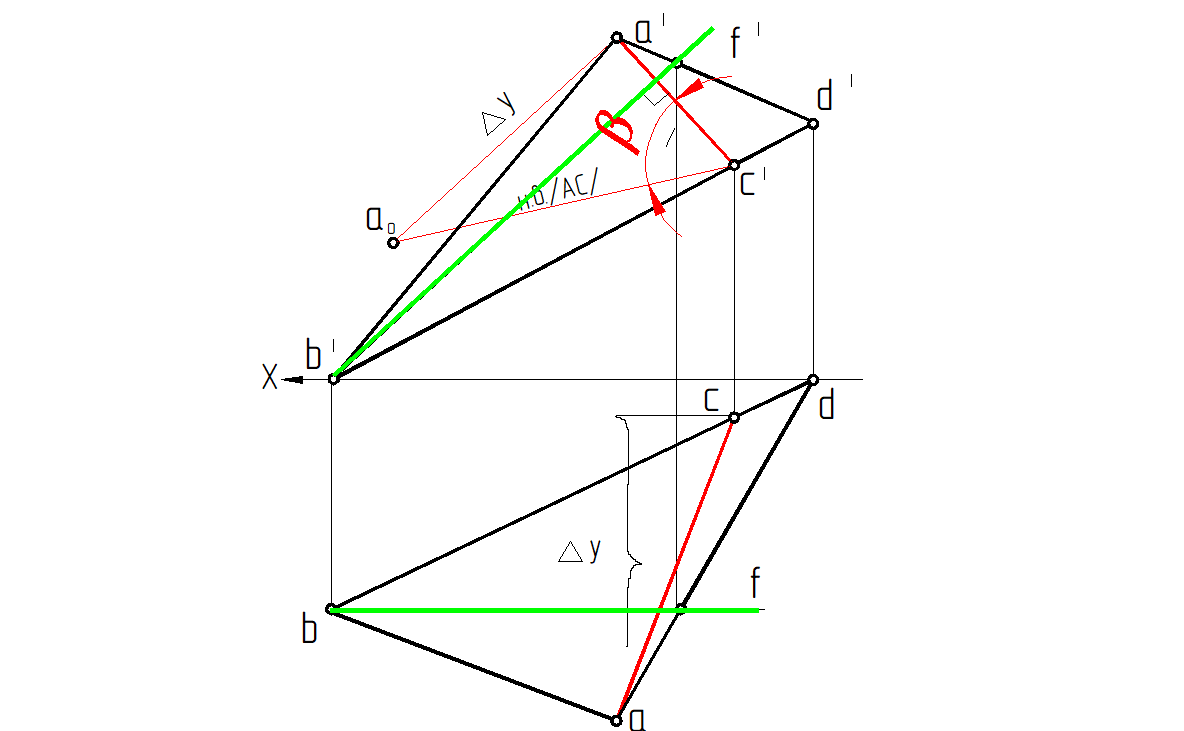
Рис. 67. Определение ∠β плоскости ∆ EAD по линии наибольшего наклона

4. Позиционные задачи

Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:

1. Задачи позиционные – решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов (в частном случае, выяснить их взаимную принадлежность) как по отношению друг к другу, так и относительно системы плоскостей проекций.

2. 3адачи метрические – при решении задач этой группы появляется возможность ответить на вопросы, касающиеся как внутренней метрики заданных геометрических объектов (определение расстояния между различными точками объекта и нахождение углов между линиями и поверхностями, принадлежащими этому объекту), так и определение расстояний между точками и величин углов между линиями и поверхностями, принадлежащими различным объектам.

3.Задачи комплексные – включают в себя элементы позиционных и метрических задач