Для этого достаточно (рис. 53, а) на проекциях плоскости взять проекции двух произвольных точек, например: m ', m и n ', n, и через них провести проекции m ' n ', mn прямой MN . На рис. 53, б проекции b ' n ', bn прямой В N проведены параллельно проекциям а'с', a с стороны АС треугольника, заданного проекциями а' b 'с', abc . Прямая В N принадлежит плоскости треугольника ABC .
| а |
| б |
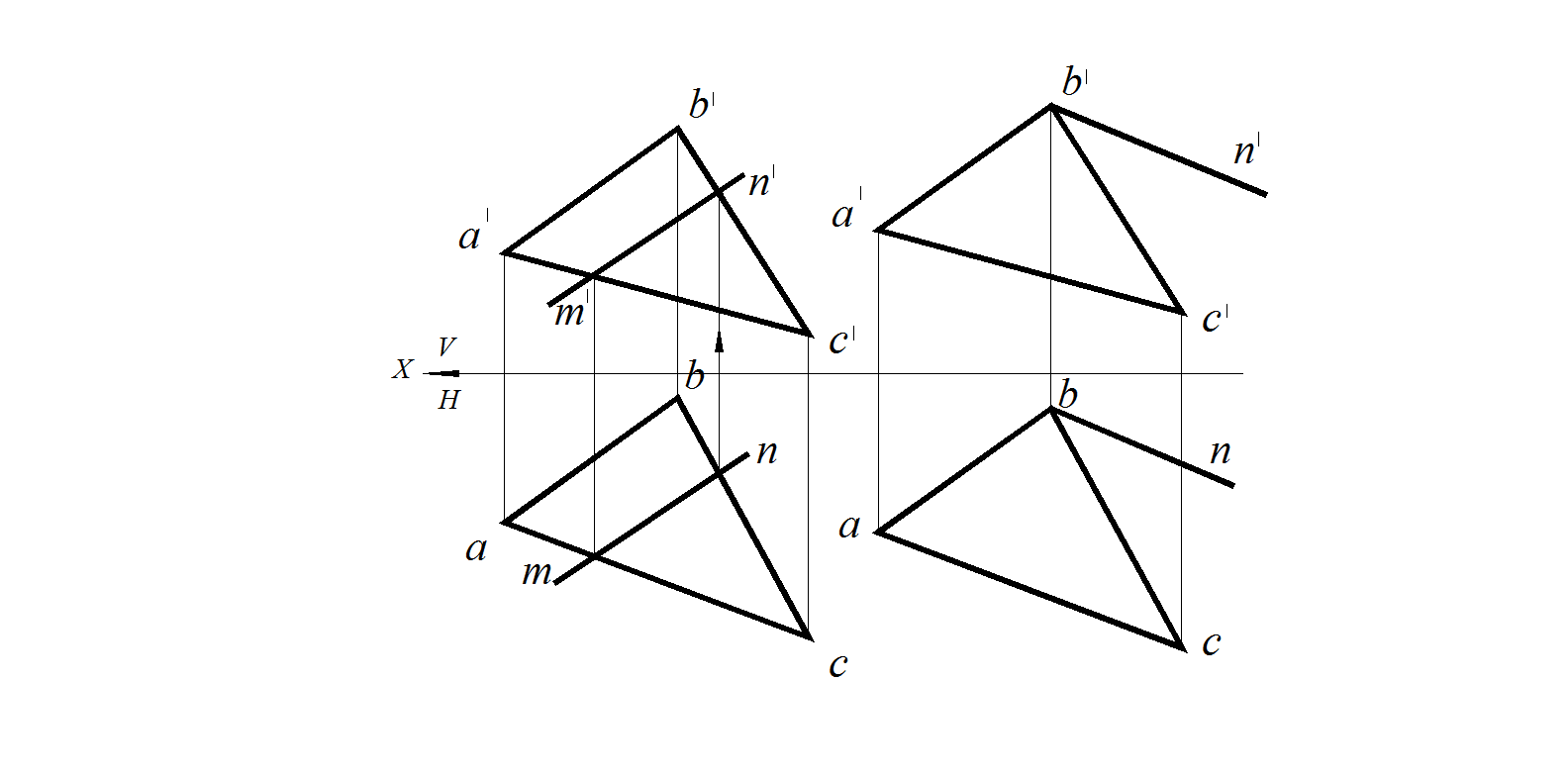
Рис. 53. Построение прямой в плоскости:
а – через две произвольные точки М и N; б – параллельно прямой АС
Построение недостающей проекции точки, принадлежащей заданной плоскости
Задача.
Построить в плоскости, заданной треугольником D ЕС, недостающие проекции точки А и точки В, принадлежащих плоскости заданного треугольника (рис. 54).
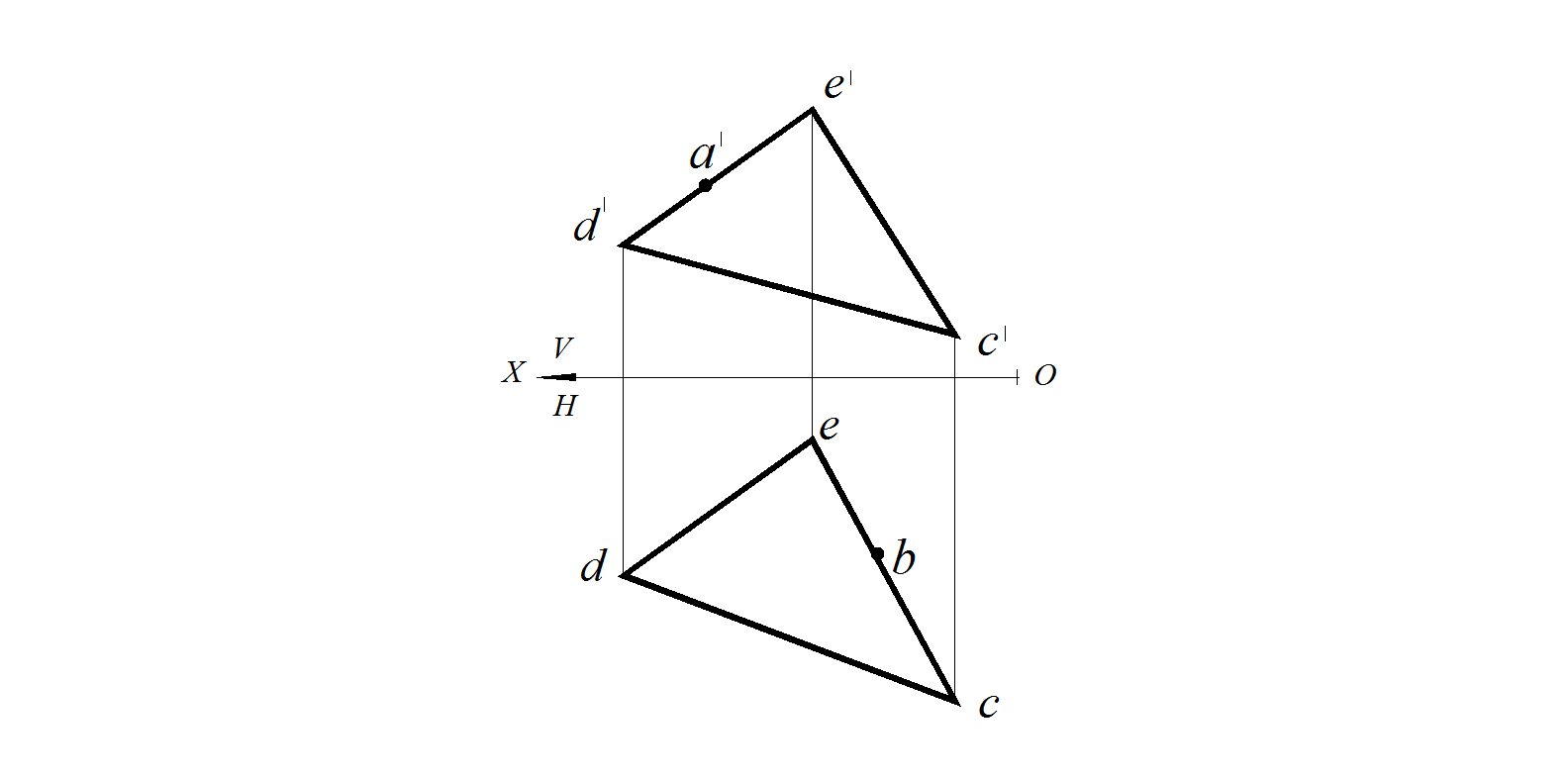
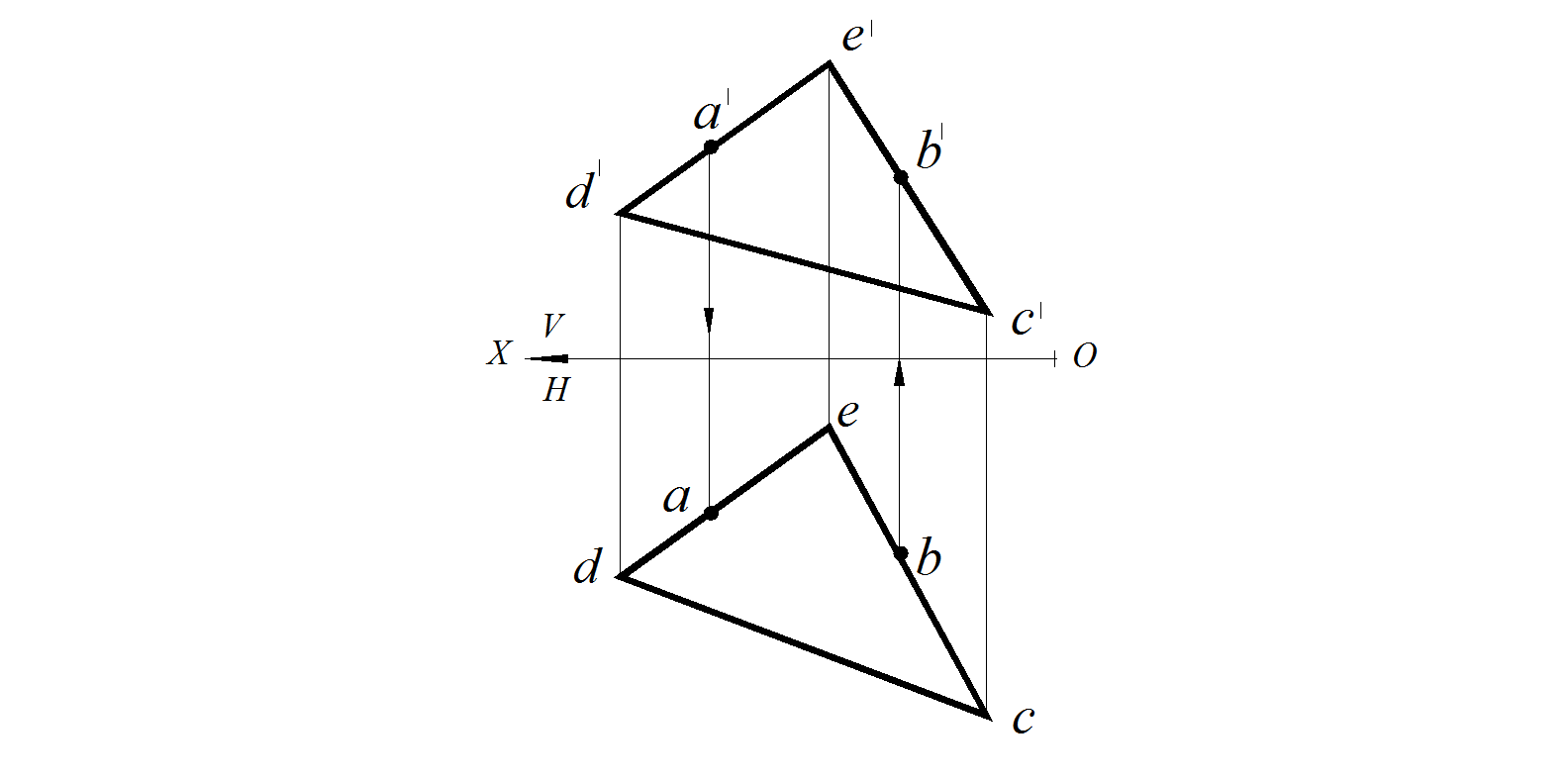
Рис. 54. Условие задачи Рис. 55. Построение в плоскости точки
Решение:
Анализируя графическое условие задачи, видим, что точка А принадлежит прямой D Е. Следовательно, по свойству принадлежности, ее горизонтальная проекция тоже принадлежит горизонтальной проекции прямой DE . Проводим линию связи из фронтальной проекции точки А до пересечения с горизонтальной проекцией прямой D Е. Полученная точка будет горизонтальной проекцией точки А. Аналогично строим фронтальную проекцию точки В (рис. 55).
Задача.
Построить фронтальную проекцию точки Е, лежащей в плоскости, заданной двумя параллельными прямыми AB и CD .
Решение:
На рис. 56 плоскость задана проекциями a ' b ' || c ' d ', ab || cd . Принадлежащая этой плоскости точка E задана горизонтальной проекцией e . Следует достроить фронтальную проекцию точки Е. Ее строят с помощью вспомогательной прямой, принадлежащей плоскости и проходящей через точку D . Такое действие называется привязкой точки к плоскости. Для этого проводят через горизонтальную проекцию d и е прямую. Отмечают точку пересечения этой прямой с прямой ab – точку n. Строят фронтальную проекцию прямой n ' d ' и по линии связи отмечают на ней фронтальную проекцию точки Е – е' (рис. 57).

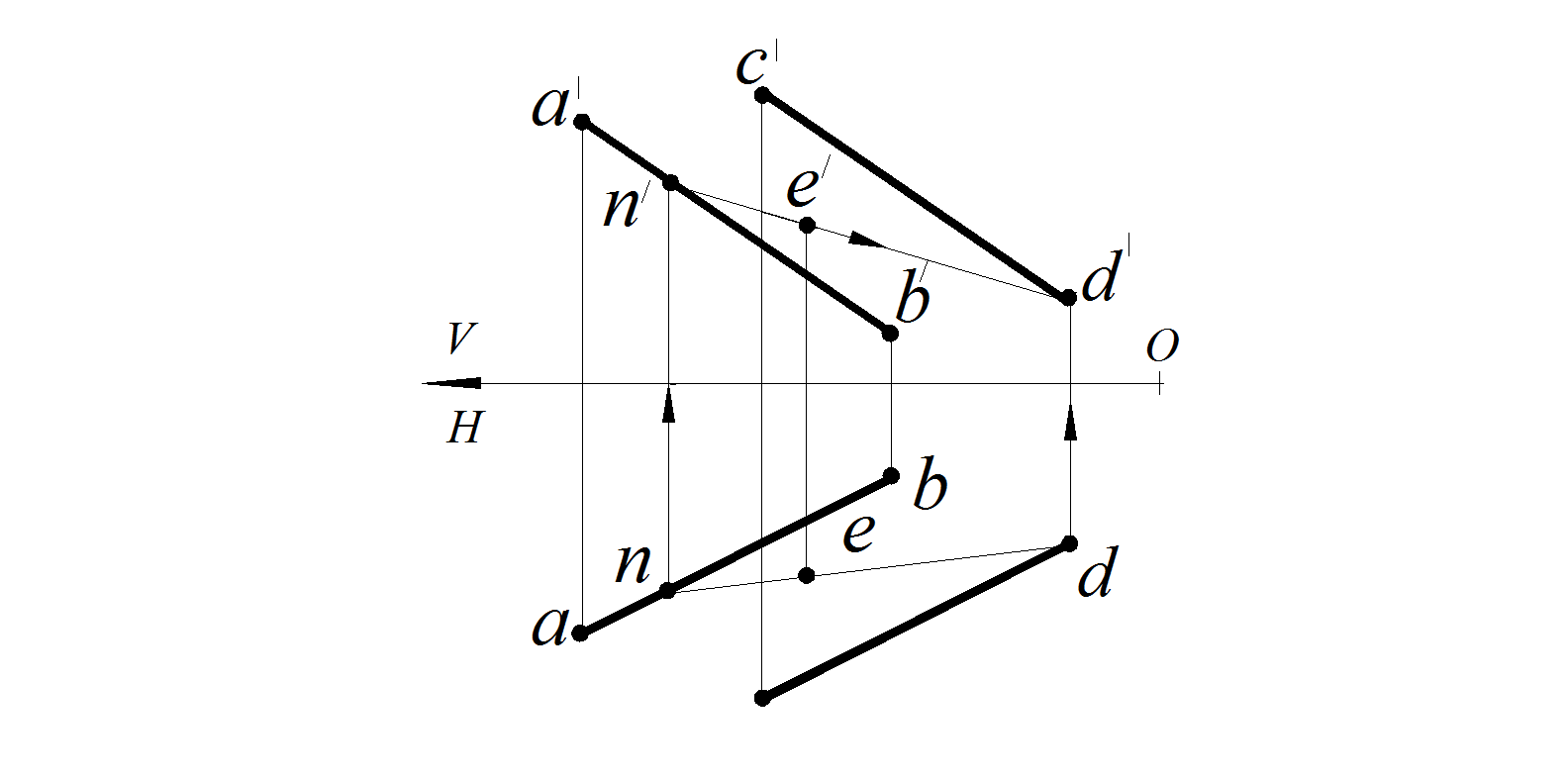
Рис. 56. Условие задачи Рис. 57. Построение недостающей
проекции точки
Проверка принадлежности точки плоскости
Задача.
Определить принадлежность точки А плоскости, заданной треугольником DFE (рис. 58).
Решение:
Для проверки принадлежности точки плоскости используют вспомогательную прямую, принадлежащую плоскости. Предполагают, что заданная точка принадлежит заданной плоскости. Следовательно, она принадлежит любой прямой, лежащей в заданной плоскости. Поэтому точку А «привязываем» к плоскости треугольника прямой. Для этого на горизонтальной проекции проводим прямую через точку а и точку b . Отмечаем точку пересечения проведенной прямой со стороной dc – точку b. Строим фронтальную проекцию полученной прямой b ' e '. Анализируя чертеж, видим, что фронтальная проекции точки А не принадлежит прямой ВЕ. Следовательно, заданная точка А не принадлежит заданной плоскости треугольника DEC. (рис. 64).
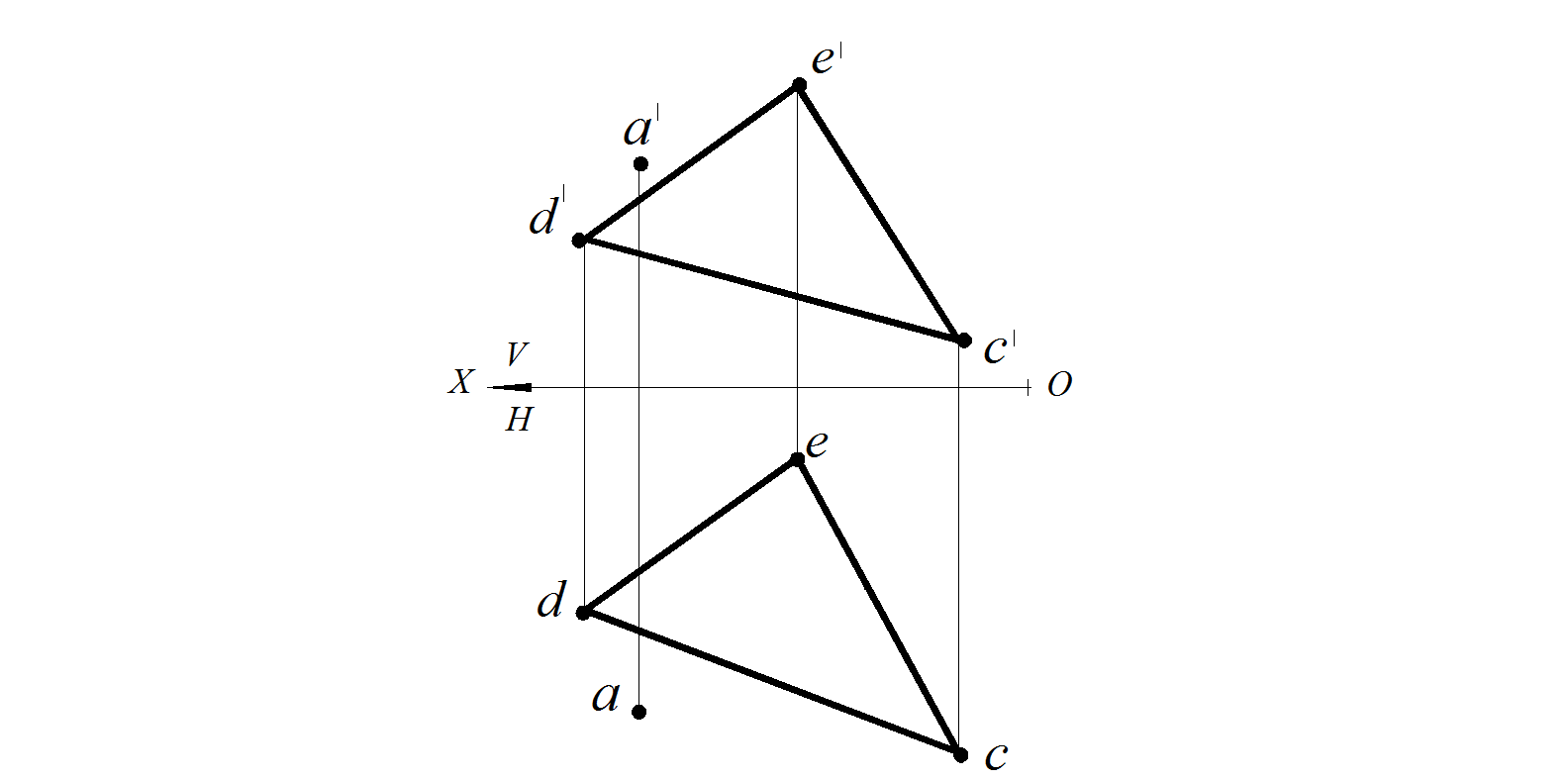
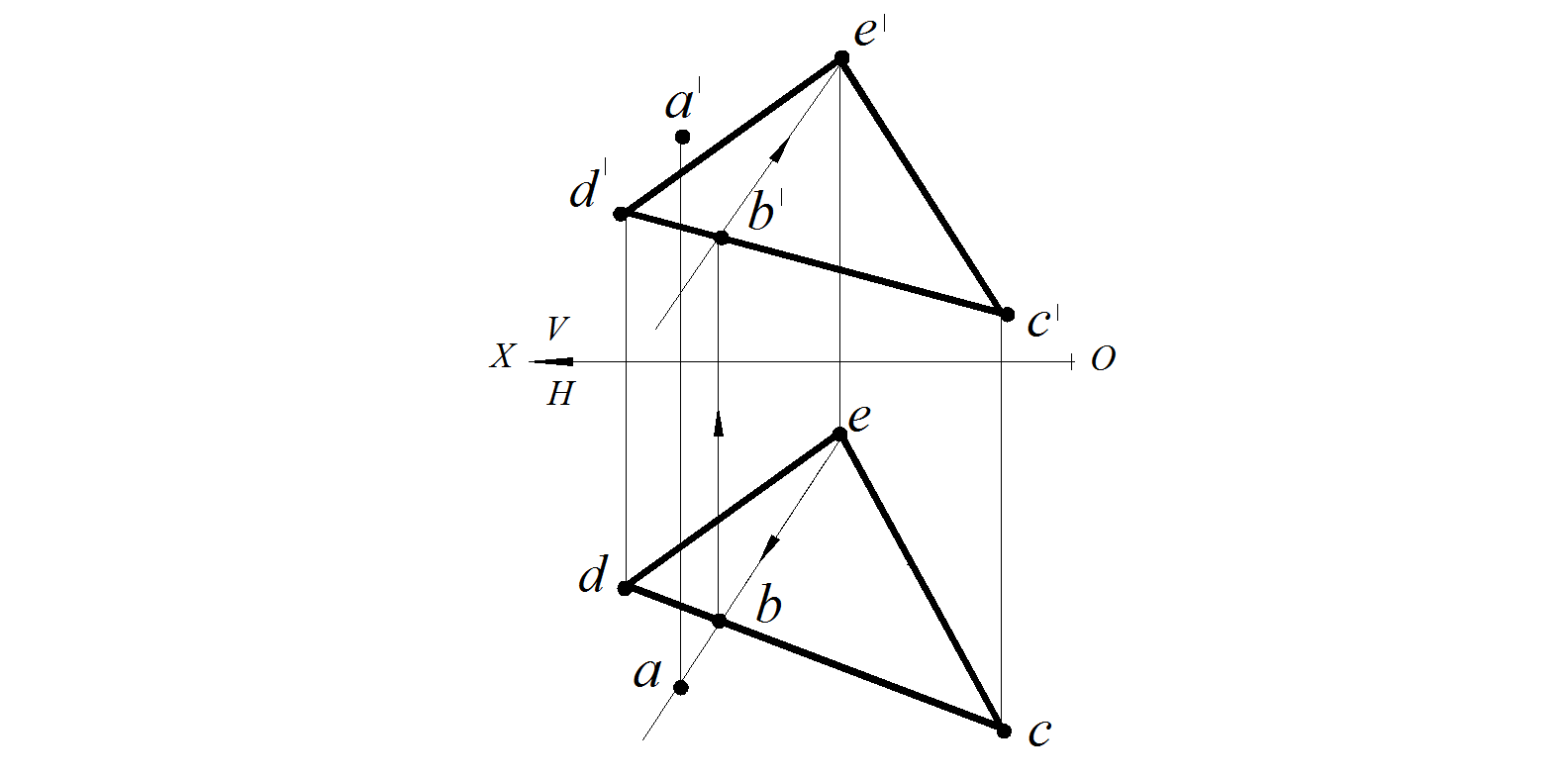
Рис. 58. Условие задачи Рис. 59. Проверка принадлежности точки плоскости
Особые линии плоскости
Особые линии плоскости
Прямые, занимающим особое положение в плоскости:
1. Линии уровня плоскости.
2. Линии наибольшего наклона плоскости к плоскостям проекций.
Линии уровня плоскости
Линии уровня плоскости – прямые, лежащие в заданной плоскости и параллельные плоскостям проекций: горизонтали, фронтали, профильные прямые.
Горизонталь плоскости – прямая, лежащая в заданной плоскости и параллельная плоскости проекций Н. Следует запомнить, что все горизонтали одной и той же плоскости параллельны между собой.
Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости, горизонтальный след плоскости является нулевой горизонталью плоскости. Чтобы построить горизонталь в плоскости Р, заданной следами, надо на фронтальной проекции Р V отметить точку d ' – фронтальную проекцию следа горизонтали (рис. 60, а). Через нее проводим фронтальную проекцию горизонтали параллельно оси х. На оси х находим горизонтальную проекцию d. Прямая, проведенная из точки d параллельно следу РН плоскости, представляет горизонтальную проекцию горизонтали.
На рис. 60, б проекции горизонтали проведены через проекции точки D и точки 1 прямой ЕС плоскости, заданной треугольником С DE . Построение горизонтали всегда начинают с фронтальной проекции d '1', которая параллельна оси Х. По свойству принадлежности находят горизонтальную проекцию точки 1 и проводят горизонтальную проекцию горизонтали.
| а |
| б |
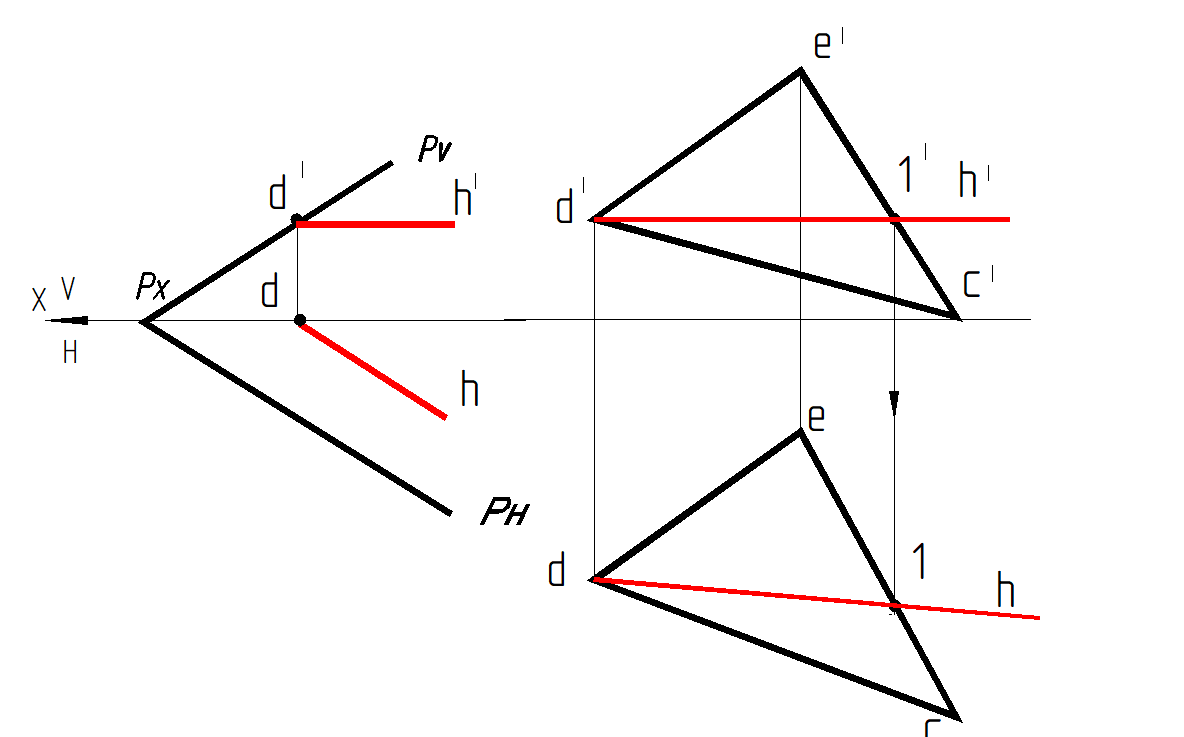
Рис. 60. Горизонталь плоскости:
а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆С DE
Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости проекций V (рис. 61).
Построение фронтали и профильных прямых выполняется аналогично построению горизонтали, опираясь на известные свойства проекций линий уровня и свойство принадлежности, и начинают его с той проекции, которая параллельна соответствующей проекционной оси. Все фронтали одной и той же плоскости параллельны между собой. То же самое можно сказать и о профильных прямых уровня плоскости.
Профильная прямая уровня плоскости – это прямая, лежащая в данной плоскости и параллельная профильной плоскости проекций (рис. 62).
| б |
| а |
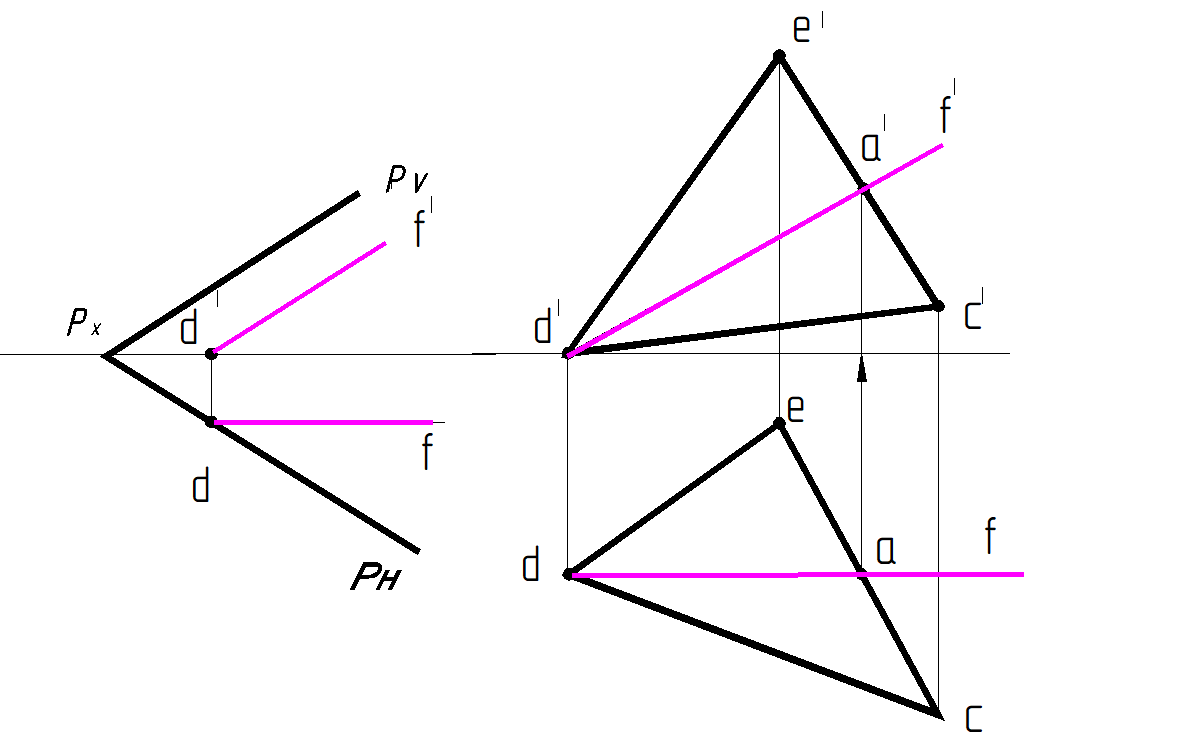
Рис. 61. Фронталь плоскости:
а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆С DE
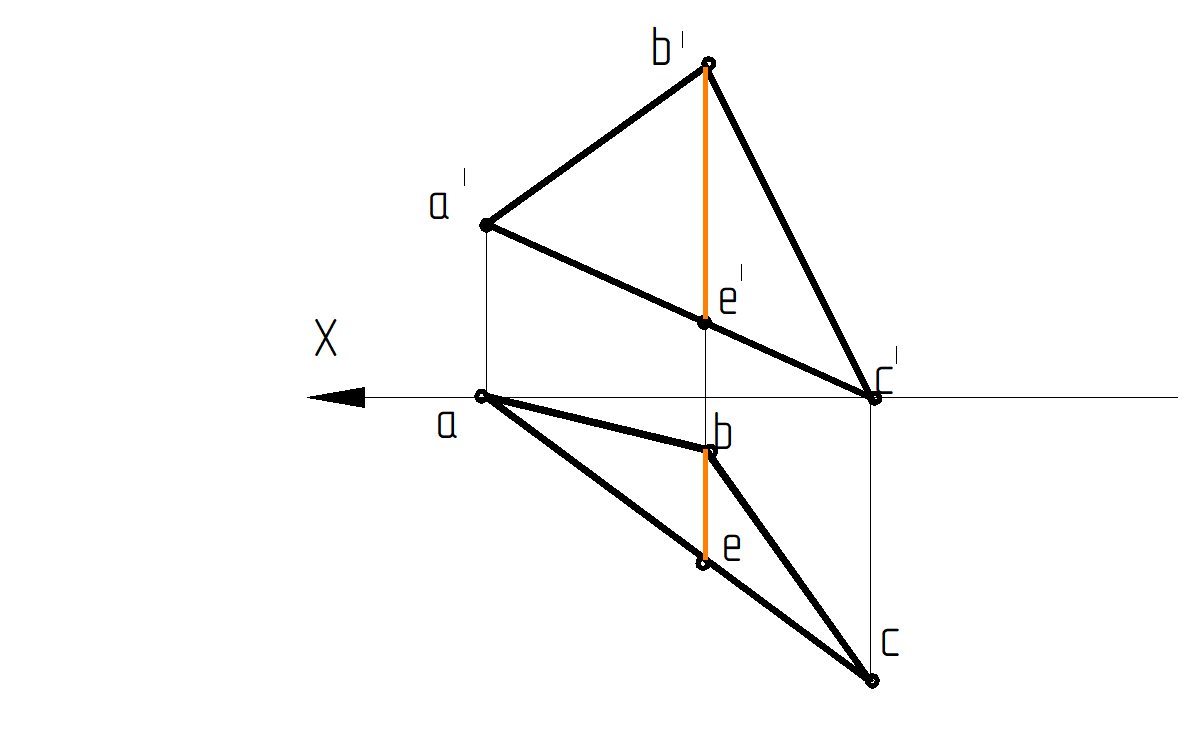
Рис. 62. Профильная прямая уровня ВЕ плоскости ∆АВС
Дата: 2018-11-18, просмотров: 1549.