Плоскостей проекций
Плоскости частного положения
Проецирующие плоскости
1. Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций Н (рис. 40–41): плоскость ΔАВС ⊥ Н; горизонтальная проекция этой плоскости – прямая а b с, совпадающая с горизонтальным следом, который располагается под углом к оси Х, соответствующим углу наклона этой плоскости к фронтальной плоскости проекций V – ∠β.
| а |
| б |
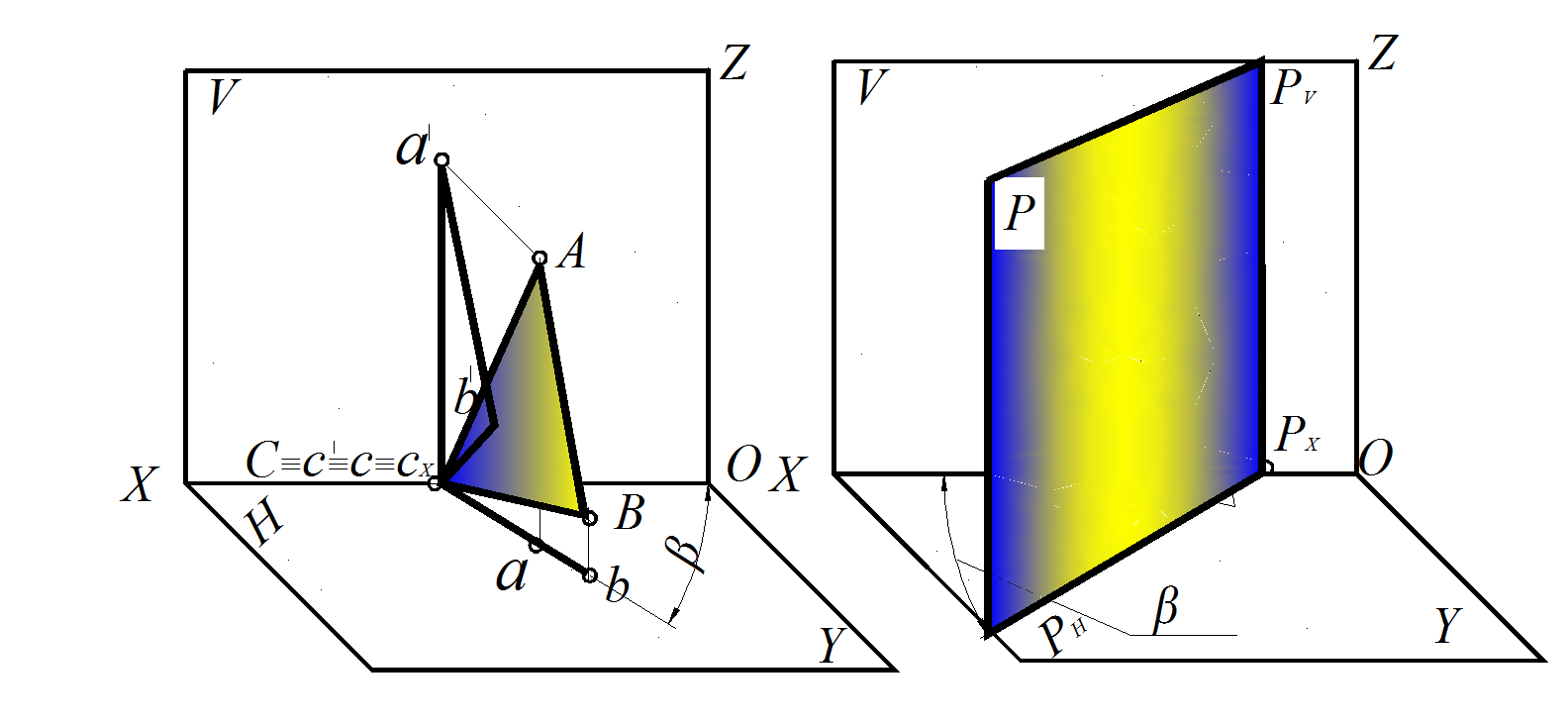
Рис. 40. Горизонтально проецирующая плоскость, пространственная модель:
а – заданная ΔАВС; б – следами плоскости Р
| б |
| а |
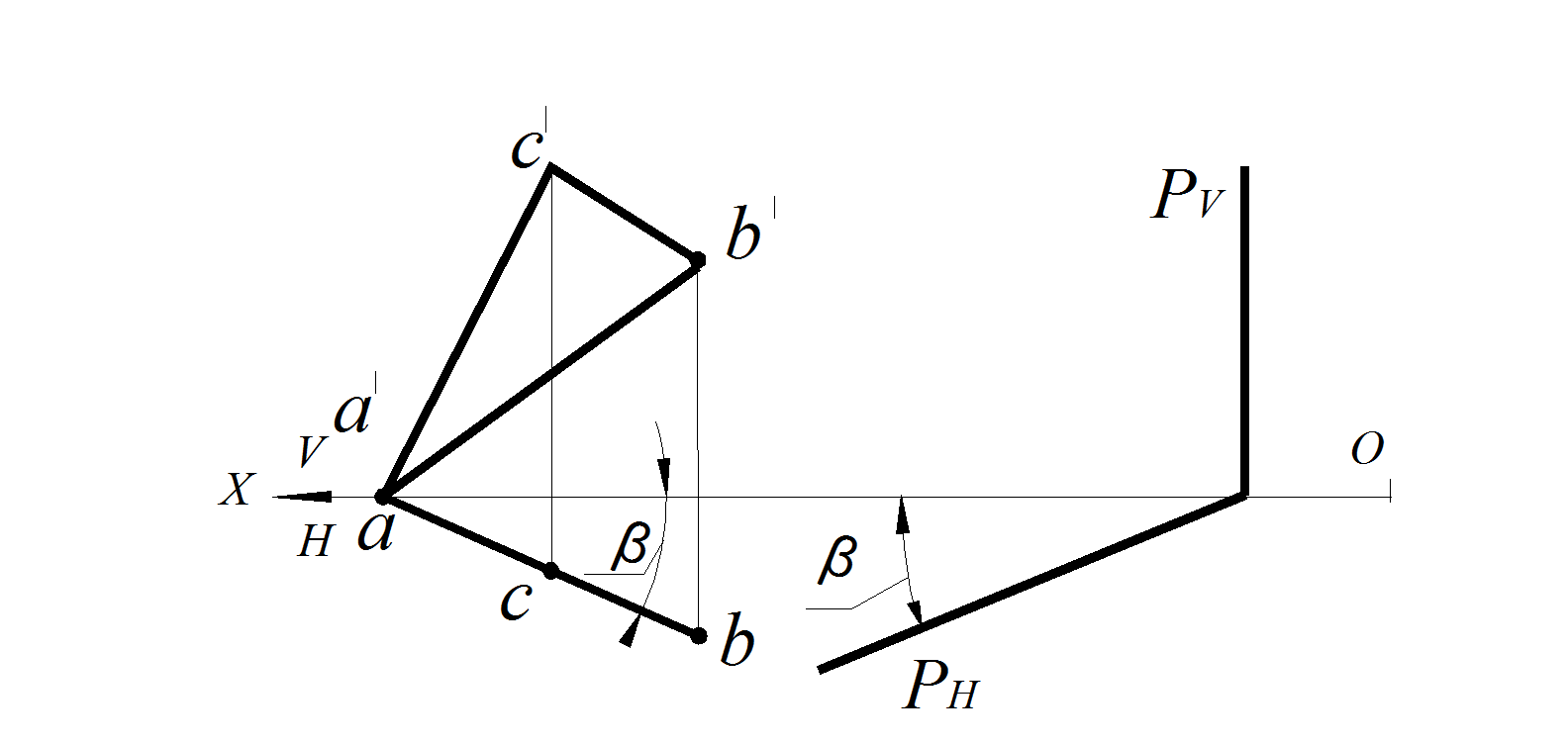
Рис. 41. Горизонтально проецирующая плоскость на эпюре:
а – заданная ΔАВС; б – следами плоскости Р
2. Фронтально проецирующая плоскость перпендикулярна плоскости проекций V (рис. 42–43): плоскость ∆ABC ⊥ V ; фронтальная проекция этой плоскости – прямая, совпадающая с фронтальным следом, который располагается под углом к оси Х, соответствующим углу наклона этой плоскости α к горизонтальной плоскости проекций Н.
| а |
| б |
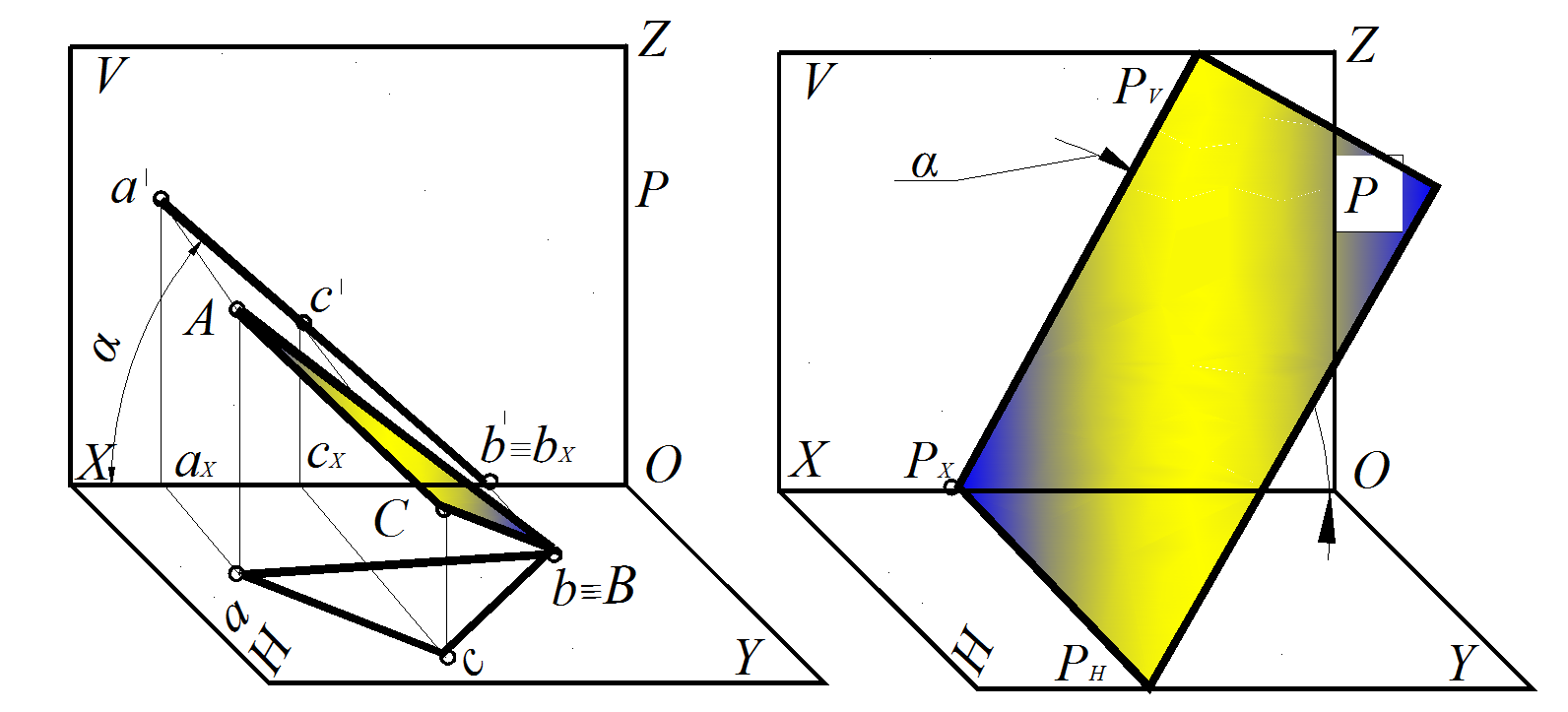
Рис. 42. Фронтально проецирующая плоскость в пространственной модели:
а – заданная ΔАВС; б – следами плоскости Р
| б |
| а |
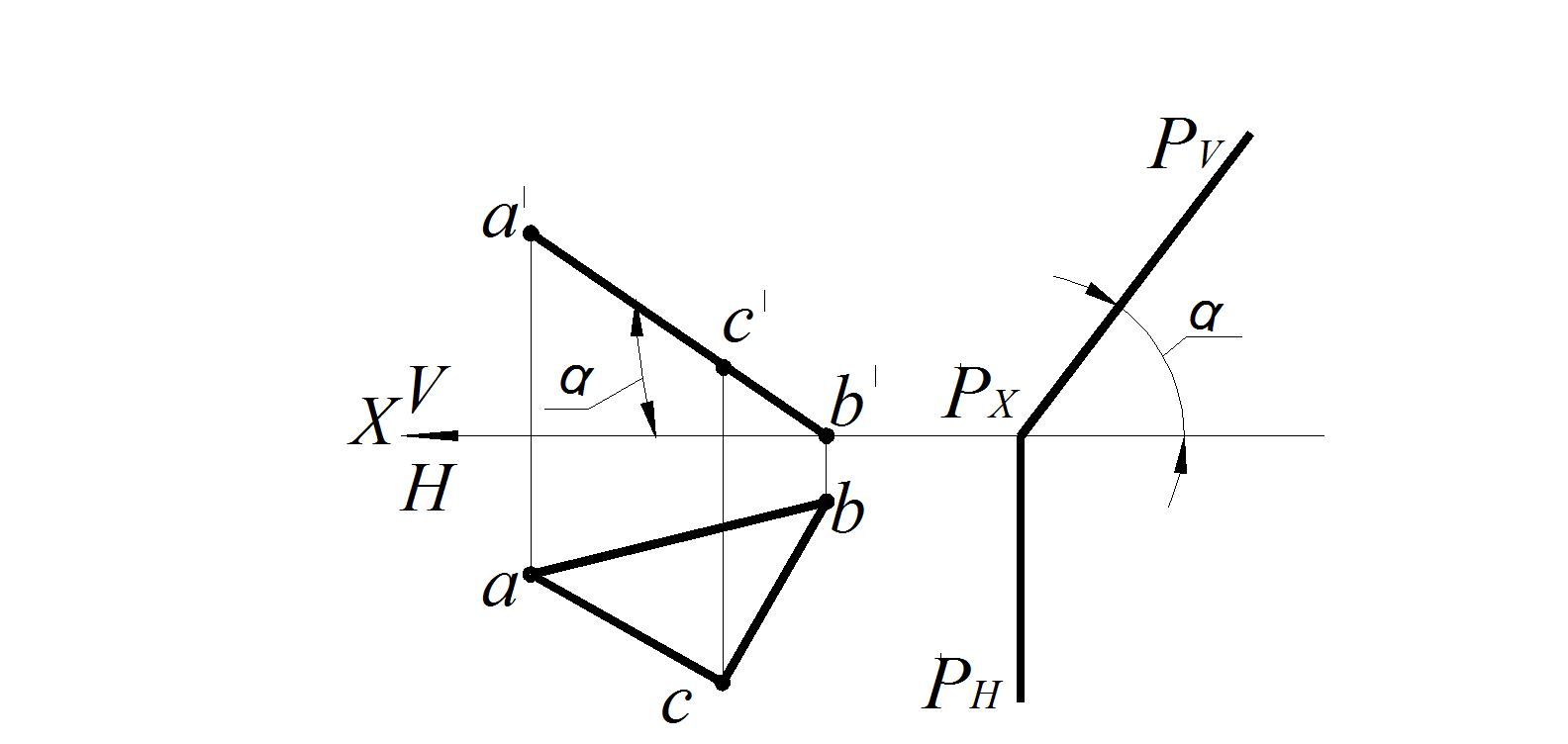
Рис. 43. Фронтально проецирующая плоскость на эпюре:
а – заданная ΔАВС; б – следами плоскости Р
3. Профильно проецирующая плоскость перпендикулярна плоскости W (рис. 44–45): ΔABC ⊥ W; профильная проекция – прямая, совпадающая со следом Р W, который располагается под углом к оси Z, соответствующим углу наклона этой плоскости β к фронтальной плоскости проекций V, под углом к оси y, соответствующим углу наклона этой плоскости α к горизонтальной плоскости проекций Н.
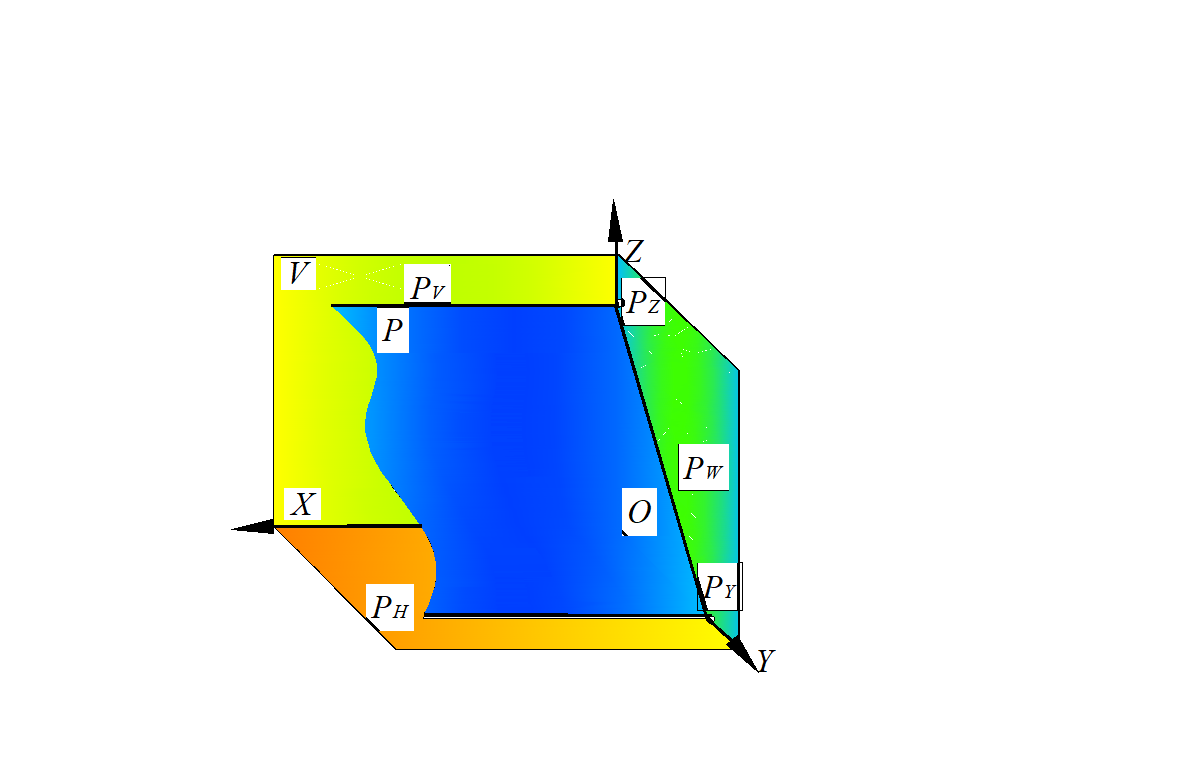
Рис. 44. Профильно проецирующая плоскость, заданная следами, в пространственной модели
| б |
| а |
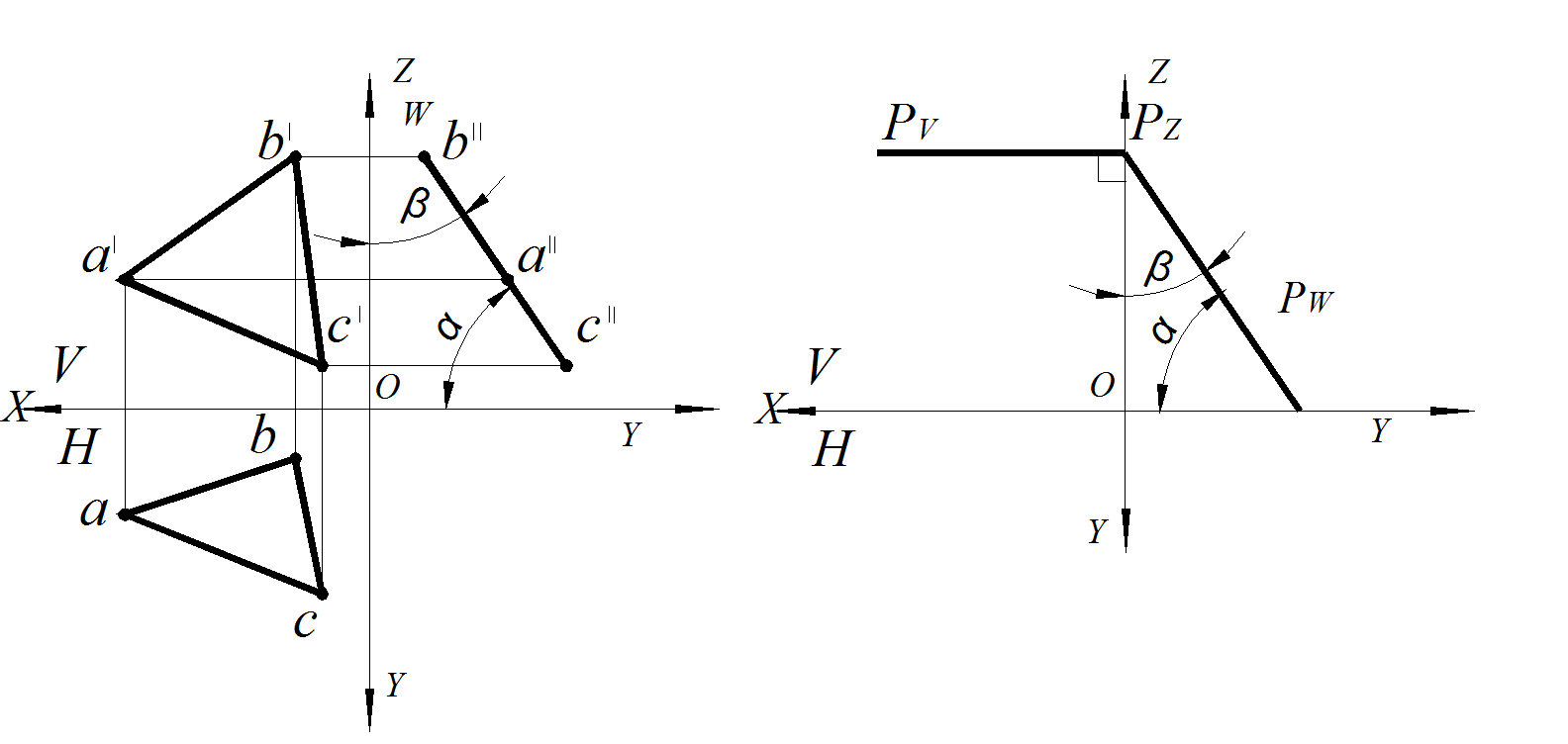
Рис. 45. Профильно проецирующая плоскость:
а – заданная ΔАВС; б – заданная следами плоскости
Свойства проецирующих плоскостей и их чертежей заключаются в следующем: плоскость проецируется в виде прямой линии на ту плоскость проекций, которой она перпендикулярна, причем угол наклона этой прямой определяет угол наклона плоскости к соответствующей плоскости проекций. Следовательно, все геометрические элементы: точки, прямые линии, плоские фигуры, лежащие в проецирующей плоскости, проецируются на эту плоскость проекций в прямую линию.
Плоскости уровня
Плоскость уровня – плоскость, параллельная какой-либо плоскости проекций (или перпендикулярная двум плоскостям проекций).
1. Горизонтальная плоскость уровня – параллельна горизонтальной плоскости проекций Н (рис. 46).
Свойства чертежа плоскости горизонтальной плоскости уровня:
– фронтальная проекция плоскости – прямая, параллельная оси Х;
– на горизонтальной проекции все элементы плоскости – прямые, углы, проецируются без искажения.
2. Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций V (рис. 47).
Свойства чертежа плоскости фронтальной плоскости уровня:
– горизонтальная проекция плоскости – прямая, параллельная оси Х;
– на фронтальной проекции все элементы плоскости – прямые, углы, проецируются без искажения.
3. Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций W (рис. 48).
| а |
| б |
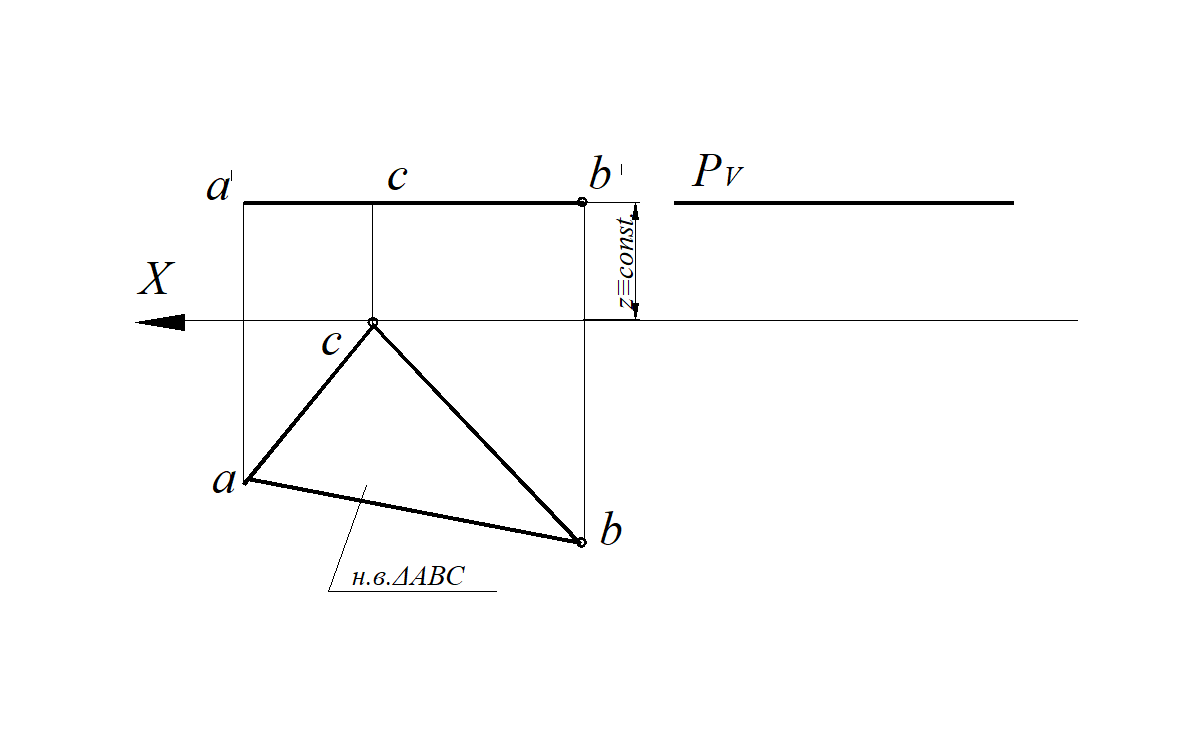
Рис. 46. Горизонтальная плоскость уровня:
а – заданная ΔАВС; б – следами плоскости Р
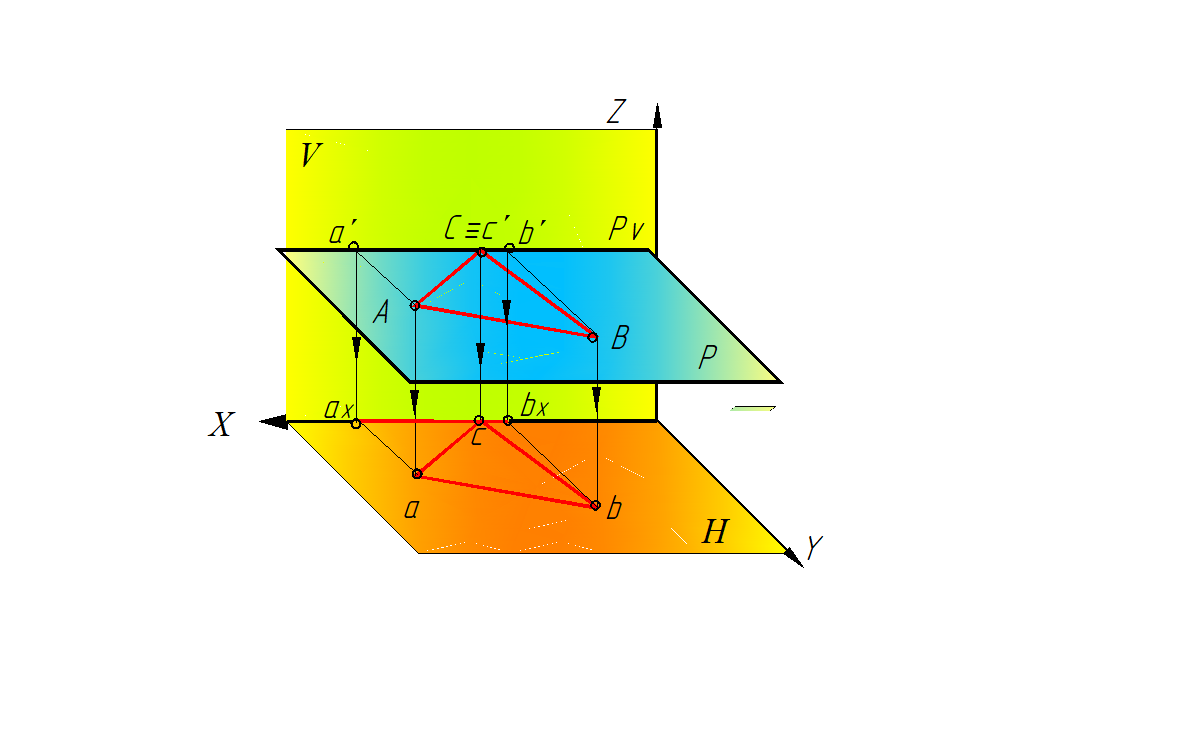
Рис. 47. Горизонтальная плоскость уровня-
пространственная модель
| а |
| б |
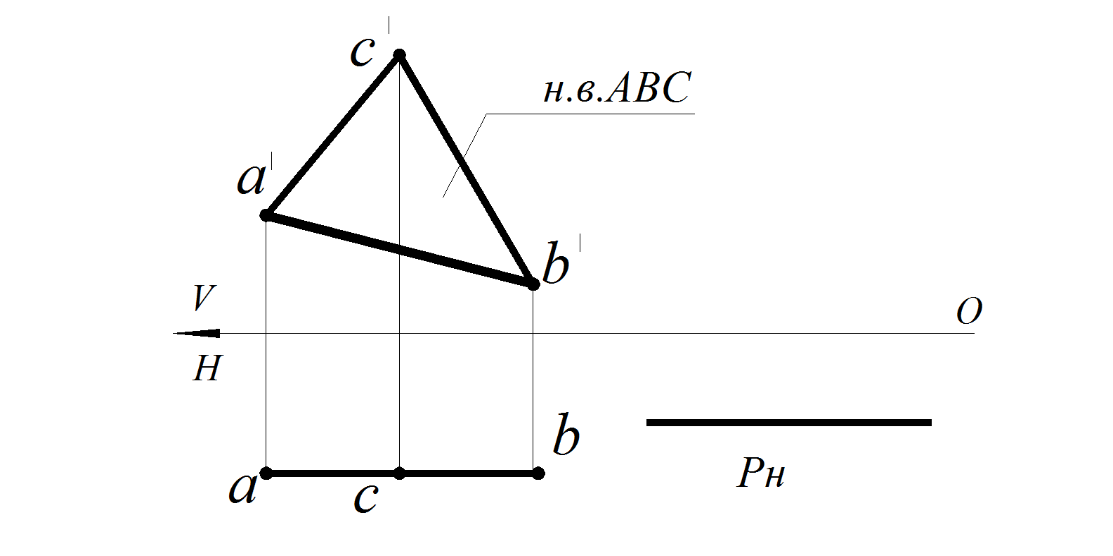
Рис. 48. Фронтальная плоскость уровня:
а – заданная ΔАВС; б – следами плоскости Р
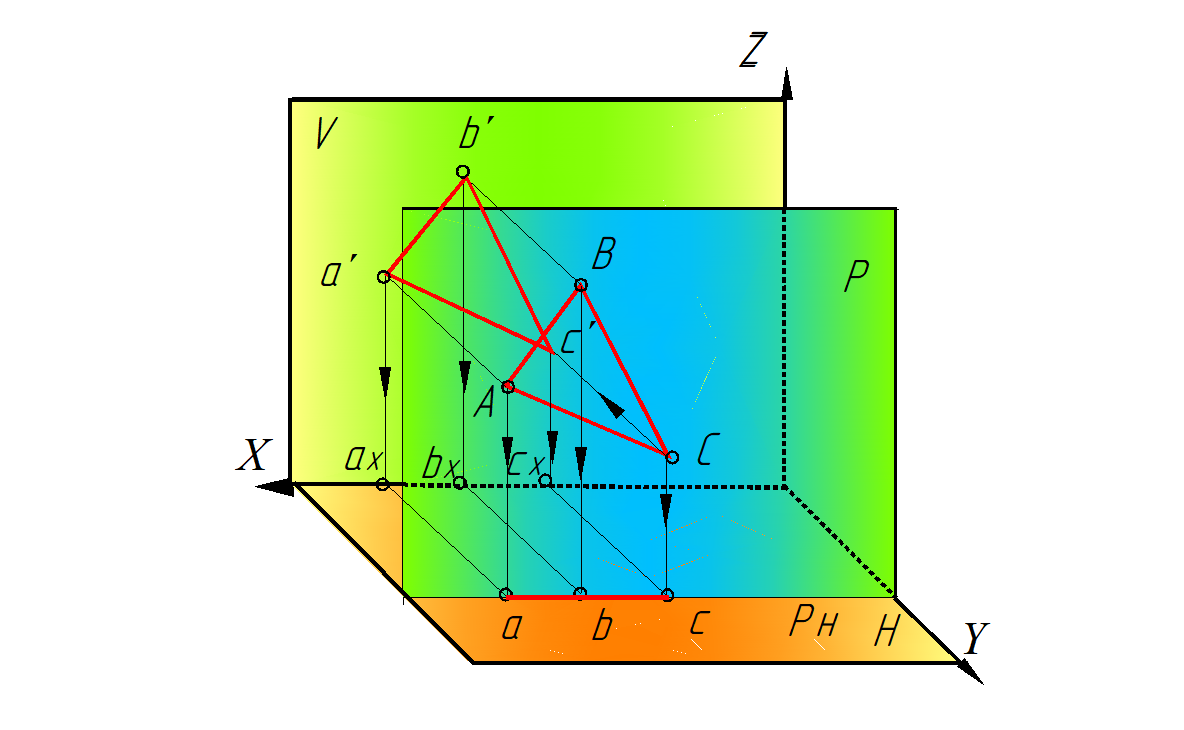
Рис. 49. Фронтальная плоскость уровня-
пространственная модель
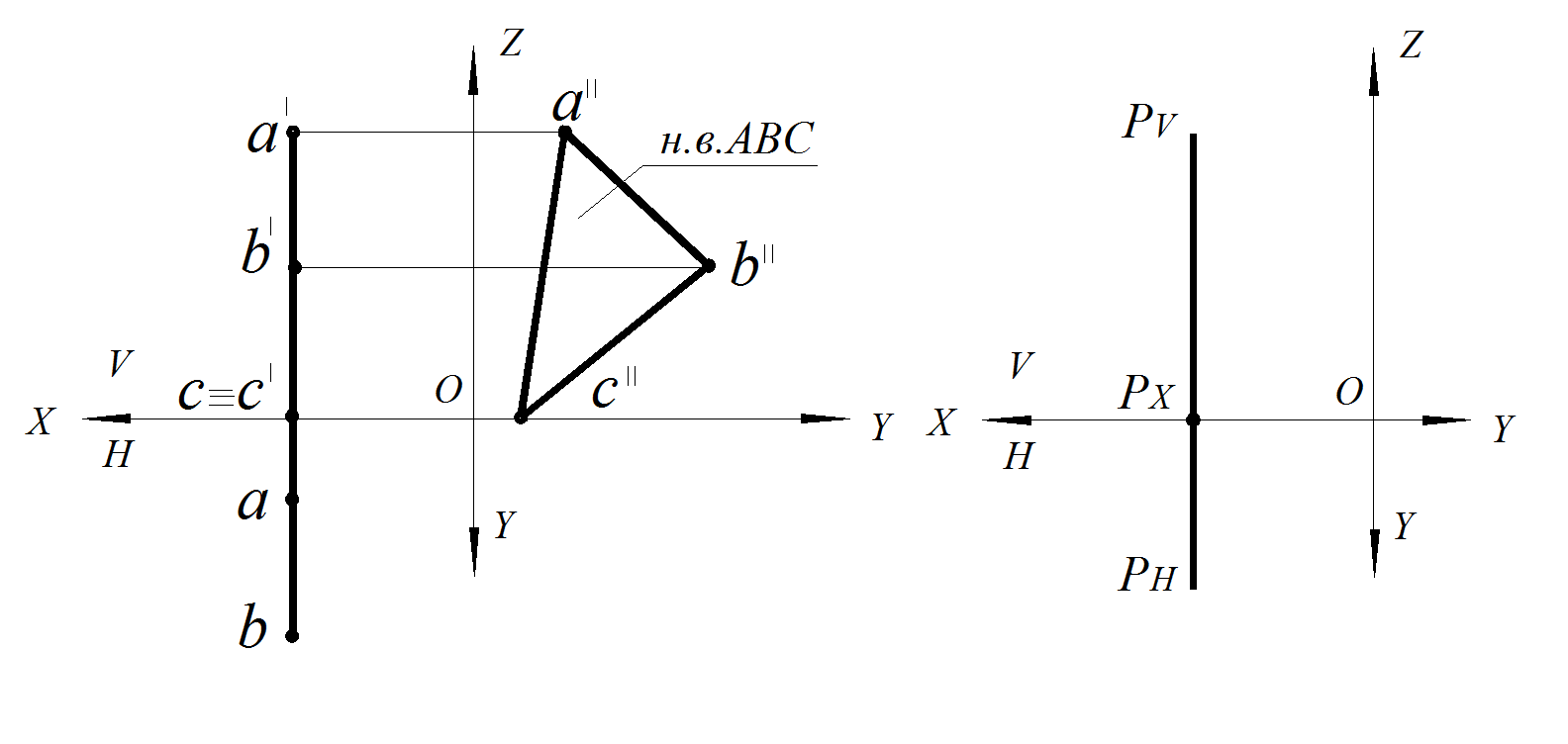
Рис.50. Профильная плоскость уровня:
а – плоскостью ΔАВС; б – заданная следами плоскости Р
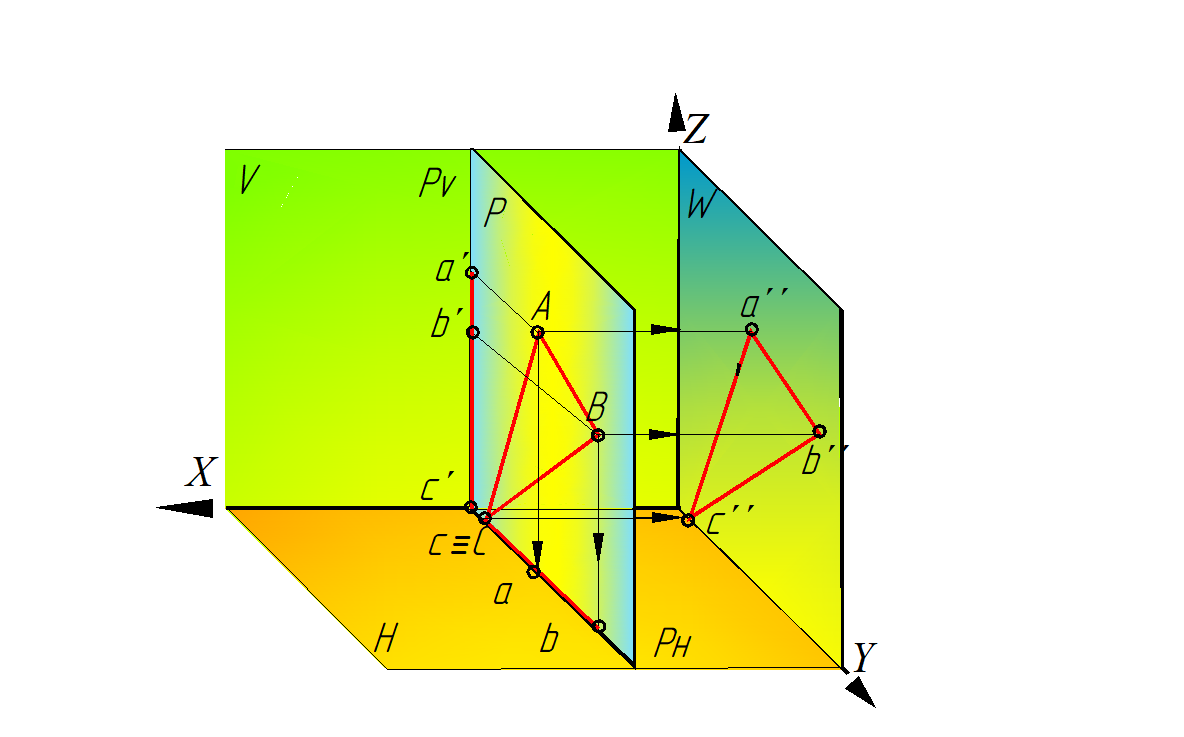
Рис. 51. Профильная плоскость уровня-
пространственная модель
Свойства чертежа плоскости профильной плоскости уровня:
а) горизонтальная проекция плоскости – прямая, параллельная оси Y и фронтальная проекция плоскости – прямая, параллельная оси Z;
б) на профильной проекции все элементы плоскости – прямые, углы, проецируются без искажения.
Следовательно, свойства чертежей плоскостей уровня таковы:
Геометрические элементы, лежащие в плоскости уровня (отрезки, плоские фигуры), проецируются в натуральную величину на ту плоскость проекций, которой они параллельны, а на две другие плоскости – в виде прямых линий, которые совпадают со своими одноименными следами.
Плоскость общего положения
Плоскость общего положения – это плоскость, не перпендикулярная ни одной плоскости проекций (рис. 52).
Свойство чертежа:
1. Ни одна из проекций плоскости общего положения не является прямой.
2. Фигура, лежащая в плоскости общего положения, отображается на плоскости проекций с искажением
.
| а |
| в |
| б |
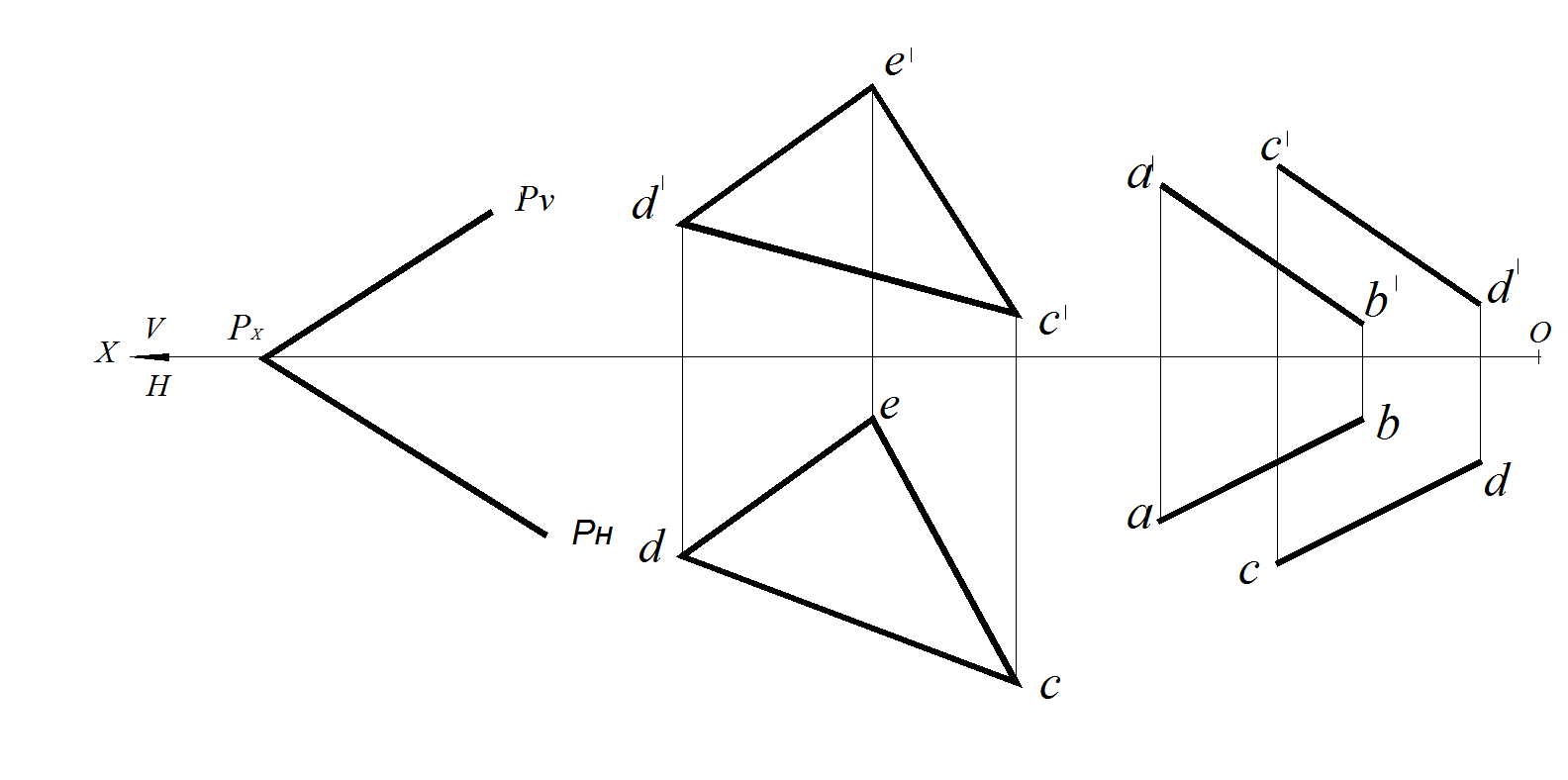
Рис. 52. Плоскость общего положения:
а – заданная следами плоскости Р; б – заданная ΔАВС; в – параллельными прямыми АВ и С D
Прямая и точка в плоскости
Построение проекций точки и прямой, принадлежащих заданной плоскости, выполняется на основании известных аксиом:
1. Через две любые различные точки можно провести только одну прямую.
2. Если две точки прямой принадлежат плоскости, то и все точки этой прямой принадлежат заданной плоскости.
Решение этих задач основывается на известных положениях геометрии:
1. Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.
2. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости, или через одну точку этой плоскости параллельно прямой, лежащей в этой плоскости или ей параллельной.
По свойству принадлежности точки прямой – ее проекции лежат на одноименных проекциях прямой, принадлежащей плоскости.
Дата: 2018-11-18, просмотров: 1190.