Если плоскость прямого угла не перпендикулярна и не параллельна плоскости проекций и хотя бы одна сторона его параллельна этой плоскости, то прямой угол проецируется на нее без искажения.
Пусть угол АВС – прямой (рис. 35) и сторона ВС || Н, следовательно, проекция bc || BC. Сторону АВ продолжим до пересечения с плоскостью Н и через точку К проводим прямую KN || bc. Следовательно, KN || BC.
Отсюда следует, что угол BKN – прямой. Согласно теореме о трех перпендикулярах, угол bKN – прямой, следовательно, угол Kbc = 90°.
Примечание: Этой теореме о проецировании прямого угла соответствуют две обратные теоремы (доказательства не приводятся).

Рис. 35. Пространственная модель проецирования прямого угла
1. Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что по крайней мере одна из сторон этого угла параллельна плоскости проекций.
2. Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет прямой угол, то проецируемый угол также прямой. На основании этих теорем можно установить, что углы, изображенные на рис. 36, в пространстве – прямые.
а б
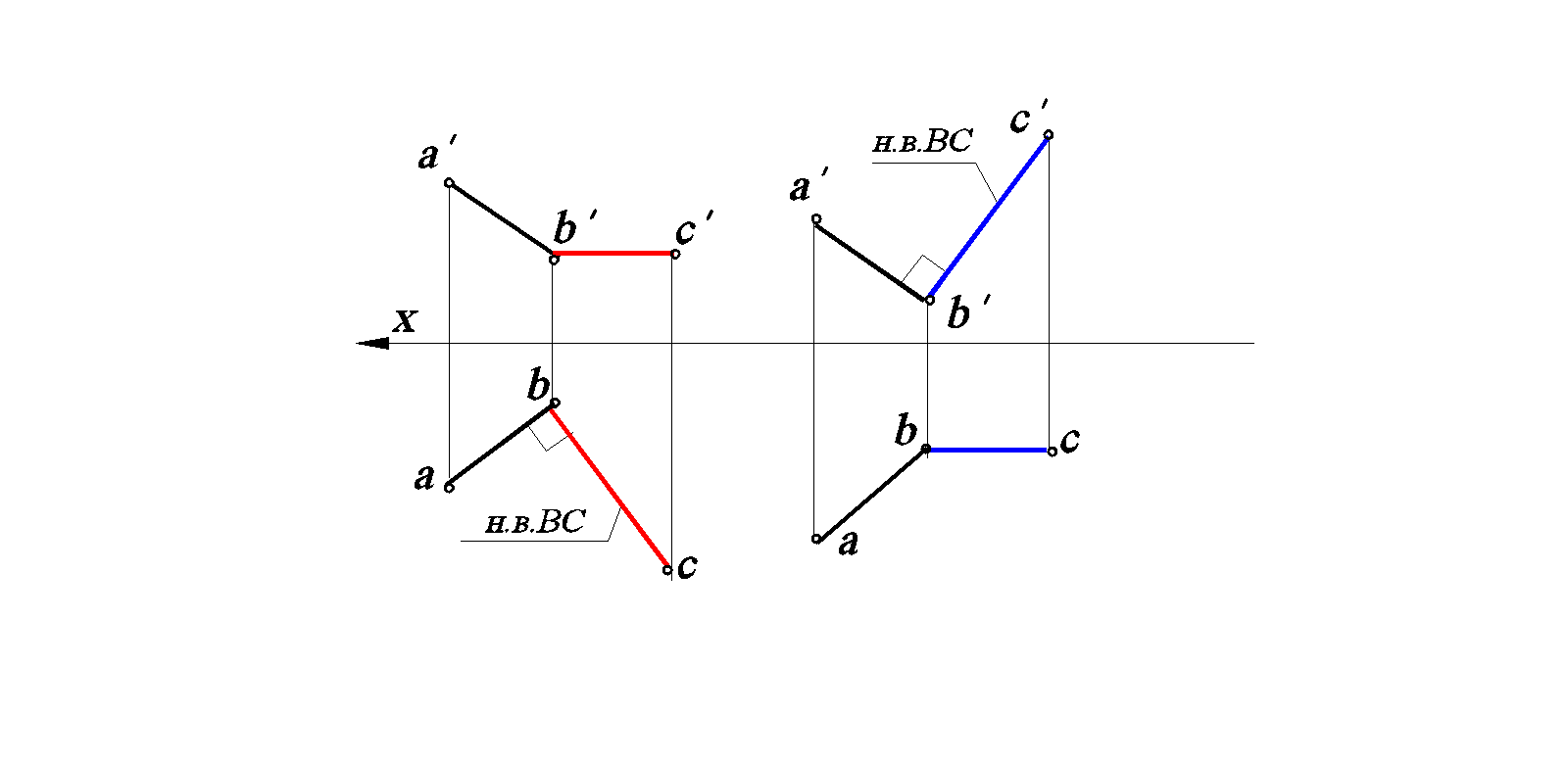
Рис. 36. Проецирование прямого угла на эпюре Монжа:
а– одна из сторон угла – горизонталь; б– одна из сторон угла – фронталь;
Из множества прямых плоскости выбираем горизонталь и фронталь плоскости, так как в этом случае на чертеже будут прямые углы, одна из сторон которых параллельна плоскости проекций
Рассмотрим угол В (рис. 36, а).
В пространстве угол В прямой, т. к. на эпюре видно, что прямая АВ является горизонталью (h ′ || X) и ∠a = 90° (согласно первой обратной теореме).
Рассмотрим угол В (рис. 36, б).
В пространстве угол В прямой, т. к. одна его сторона является фронталью (АВ || V; ab || X) и фронтальная проекция ∠b′ = 90°.
Из этой теоремы следует простой вывод – к прямой можно провести перпендикуляр там, где прямая проецируется в натуральную величину.
При решении позиционных и метрических задач начертательной геометрии, опираясь на эти теоремы, можно строить две взаимно перпендикулярные прямые, что, в конечном итоге, позволяет определять расстояния, строить взаимно перпендикулярные плоскости.
3. Плоскость
Способы задания плоскости. Плоскости частного и общего положения. Свойства чертежа плоскостей частного положения. Прямая и точка в плоскости. Особые линии плоскости.
Плоскость – одно из основных понятий геометрии. Плоскость в линейной алгебре – поверхность первого порядка, может быть задана уравнением 1-й степени:
Ax + By + Cz + D = 0
Способы задания плоскости
Аксиомы, определения, теоремы курса стереометрии
Аксиома 1. Через любые две точки проходит одна и только одна прямая линия.
Аксиома 2. Прямая, проходящая через две различные точки плоскости, лежит в этой плоскости.
Аксиома 3. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
Аксиома 4. Если две различные плоскости имеют общую точку, то их пересечение есть прямая.
Следствия из аксиом
Следствие 1. Через прямую и не принадлежащую ей точку можно провести одну и только одну плоскость.
Следствие 2. Через две пересекающиеся прямые можно провести одну и только одну плоскость.
Две прямые называются пересекающимися, если они имеют единственную общую точку.
Следствие 3. Через две различные параллельные прямые можно провести только одну плоскость.
Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общей точки или совпадают.
Способы задания плоскости на чертеже
1. Плоскость может быть задана тремя точками (рис. 37, а).
2. Плоскость может быть задана точкой и прямой (рис. 37, б).
3. Плоскость может быть задана двумя пересекающимися прямыми (рис. 38, а).
4. Плоскость может быть задана двумя параллельными прямыми (рис. 38, б).
5. Плоскость может быть задана любой плоской фигурой (рис. 39, а).
6. Плоскость может быть задана следами (след плоскости – это линия пересечения данной плоскости с какой-либо из плоскостей проекций, рис. 39, б); PH – горизонтальный след плоскости Р; PV – фронтальный след плоскости Р; PX – точка пересечения следов.
| а |
| б |

Рис. 37. Способы задания плоскости на чертеже:
а – тремя точками А, В, С; б – точкой А и прямой ВС
| а |
| б |

Рис. 38. Способы задания плоскости на чертеже:
а – параллельными прямыми АВ и CD; б – пересекающимися прямыми М N и EF
| в |
| б |
| а |

Рис. 39. Способы задания плоскости на чертеже:
а – треугольником АВ C; б – следами плоскости Р; в – нулевой фронталью и горизонталью плоскости Т
Горизонтальный след плоскости называют нулевой горизонталью, фронтальный след – нулевой фронталью. Горизонтальный след плоскости лежит в горизонтальной плоскости проекций, следовательно, точка D, лежащая на горизонтальном следе плоскости Р тоже лежит на горизонтальной плоскости проекций Н. Фронтальный след плоскости лежит во фронтальной плоскости проекций V, следовательно, точка Е, лежащая на фронтальном следе плоскости Р, тоже лежит на фронтальной плоскости проекций V (рис. 39, б). Плоскость Т задана непосредственно нулевыми фронталью и горизонталью (рис. 39, в).
Дата: 2018-11-18, просмотров: 1163.