Установлена зависимость между действительной (натуральной) величиной отрезка и его проекциями. На основании этой зависимости выведено правило прямоугольного треугольника, из которого следует, что для определения действительной величины отрезка прямой, на эпюре достаточно построить прямоугольный треугольник у которого за один катет берется проекция отрезка (фронтальная или горизонтальная), а другим катетом является величина отрезка, равная разности расстояний концов этого отрезка до одной из плоскостей проекций V или Н. Действительной величиной отрезка является гипотенуза построенного треугольника, а угол между гипотенузой и проекцией этого отрезка является углом наклона его плоскости к плоскостям проекций V или Н. В зависимости от того, на какой из проекций выполняется построение, именно, к той плоскости проекций определяется угол наклона плоскости треугольника.
Если необходимо определить ∠α отрезка прямой, прямоугольный треугольник строят, используя горизонтальную проекцию отрезка
Если необходимо определить ∠β отрезка прямой, прямоугольный треугольник строят, используя фронтальную проекцию отрезка.
Если по условию задачи требуется определить только натуральную величину отрезка общего положения, то для решения задачи можно использовать любую из проекций.
Рассмотрим несколько типовых задач, связанных с использованием этого метода.
Задача 1.
Определить длину отрезка прямой АВ и угол наклона его к горизонтальной плоскости проекций Н ( ∠ αАВ) (рис. 28).
Решение:
Необходимо проанализировать графическое и словесное условие задачи:
1. Графический анализ проводится относительно осей проекций: отрезок прямой АВ занимает общее положение, т. к. ни одна проекция отрезка прямой не является характерной (параллельной или перпендикулярной оси Х). Следовательно, ни одна проекция отрезка не дает нам натуральной величины данного отрезка непосредственно на чертеже.
2. Словесное условие говорит о том, что дополнительные построения необходимо выполнять на горизонтальной проекции отрезка, т. к. требуется найти угол наклона отрезка к горизонтальной плоскости проекций – ∠αАВ. В этом случае прямоугольный треугольник нужно строить, принимая за один его катет горизонтальную проекцию аb.
Далее, графические построения выполняются по приведенному ниже плану.
Порядок выполнения графической части задачи:
1. Проводим луч [а) ⊥ [аb] (либо из точки b).
2. Находим величину второго катета – |аАо| = ZА – ZВ = ∆Z (разность удаления концов отрезка до горизонтальной плоскости проекций).
3. Гипотенуза Аоb равна натуральной величине отрезка АВ |AB| = |Aob| = 40 мм.
4. Угол между гипотенузой |Aob| и проекцией |ab| является углом наклона отрезка АВ к плоскости проекций Н – αАВ.
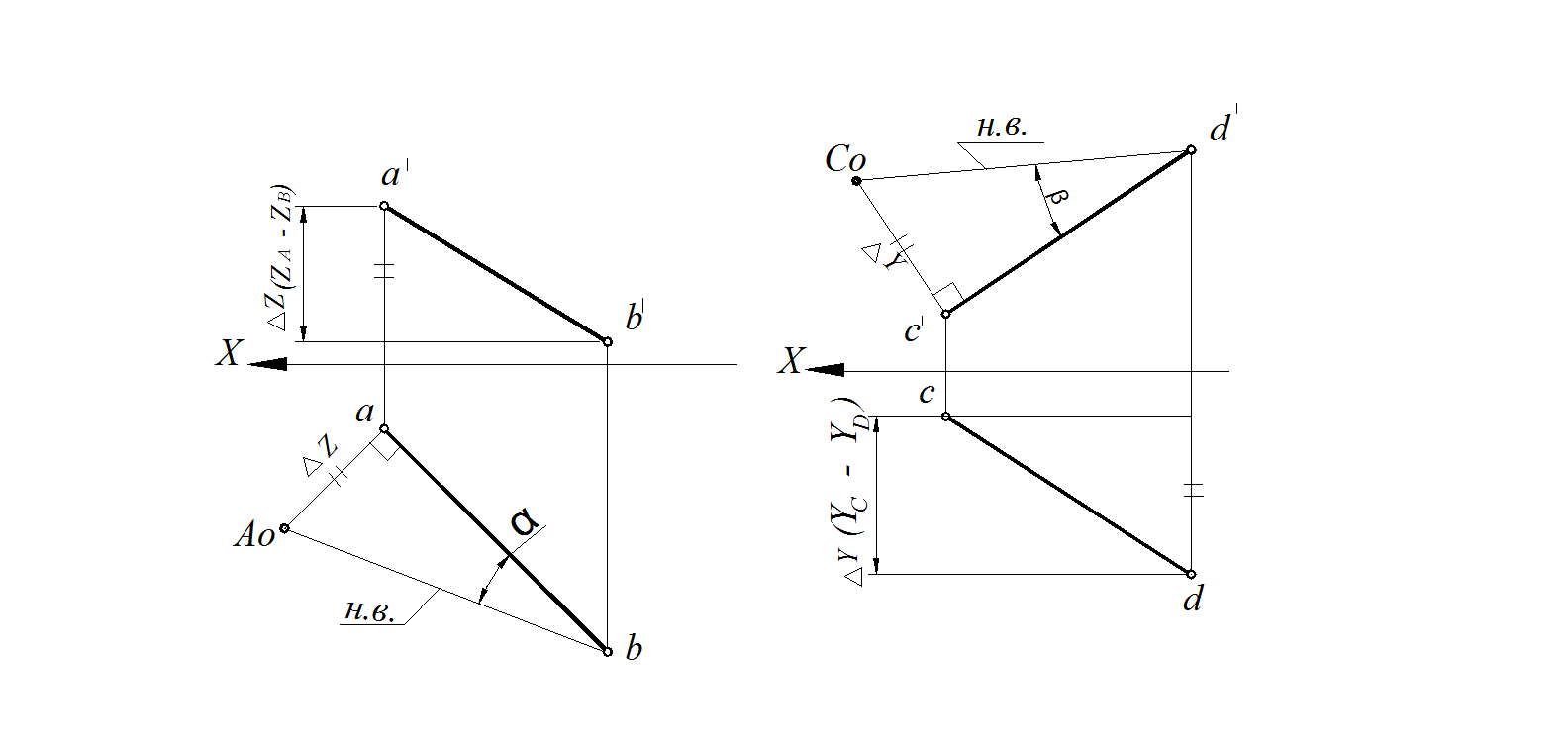
Рис. 28. Определение ∠αАВ Рис. 29. Определение ∠βС D
Задача 2.
Определить угол наклона отрезка СD к плоскости проекций V (рис. 29).
Решение.
Анализ условия задачи аналогичен задаче, рассмотренной выше.
При определении угла наклона отрезка прямой к плоскости проекций V прямоугольный треугольник нужно строить, принимая за один его катет фронтальную проекцию данного отрезка, а величина второго катета представляет собой разность расстояний концов отрезка до фронтальной плоскости проекций, т. е. разница координат Y.
Порядок выполнения графической части задачи:
1. Проводим луч [c') ⊥ [c'd'] (либо из точки d').
2. Откладываем на луче [c') величину второго катета |c'Co| = Y С – YD = ∆Y .
3. Гипотенуза Cod' с отрезком c'd' образует ∠β, являющийся углом наклона [CD] к плоскости проекций V – ∠βС D.
Взаимное положение прямых
Прямые в пространстве могут занимать различные положения относительно друг друга: быть параллельными, пересекаться и скрещиваться.
Пересекающиеся прямые
Если прямые пересекаются в пространстве в определенной точке, то их одноименные проекции пересекаются в проекциях этой же точки (рис. 30).
Если АВ ∩ CD = (∙) I => ab ∩ cd = 1; a ′ b′ ∩ c ′ d′ = 1′a ′′ b′′ ∩ c ′′ d′′ = 1′′.
Правильным будет и обратное утверждение: если на чертеже одноименные проекции прямых пересекаются, а проекции точки их пересечения лежат на одной линии связи, то прямые пересекаются в пространстве в этой же точке.
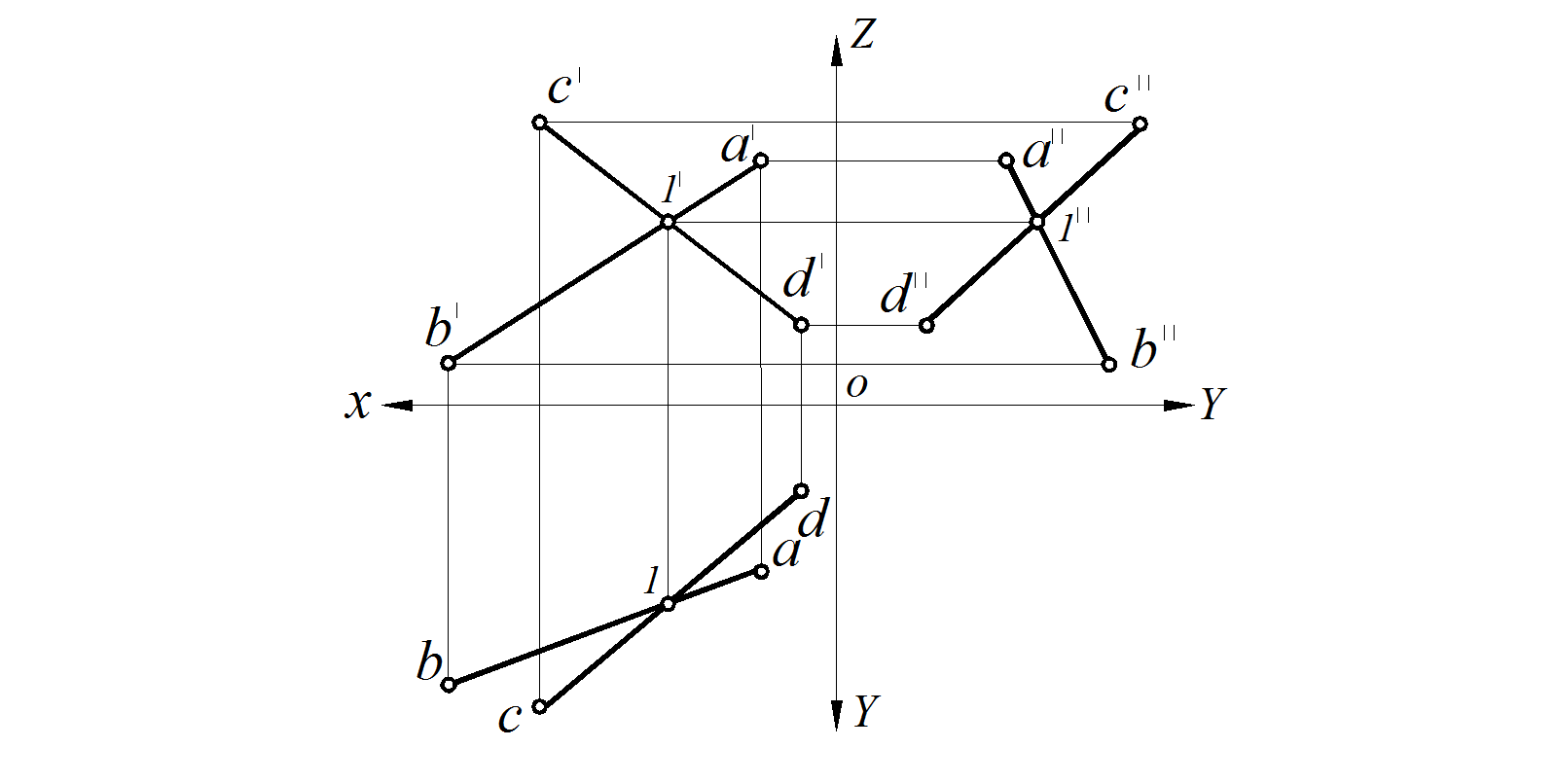
Рис. 30. Пересекающиеся прямые АВ и С D
Параллельные прямые
По свойству параллельного проецирования известно, что одноименные проекции параллельных прямых параллельны между собой. Рассмотрим данное свойство на примере параллельных отрезков прямых АВ и С D.
Дано АВ || С D, следовательно, на чертеже их одноименные проекции будут параллельны между собой (рис. 31): ab || cd, a ′ b′ || c ′ d ′ , a ′′ b ′′ || c ′′ d ′′, а также этому свойству соответствует обратное свойство: если на чертеже одноименные проекции прямых параллельны между собой, то в пространстве эти прямые параллельны.
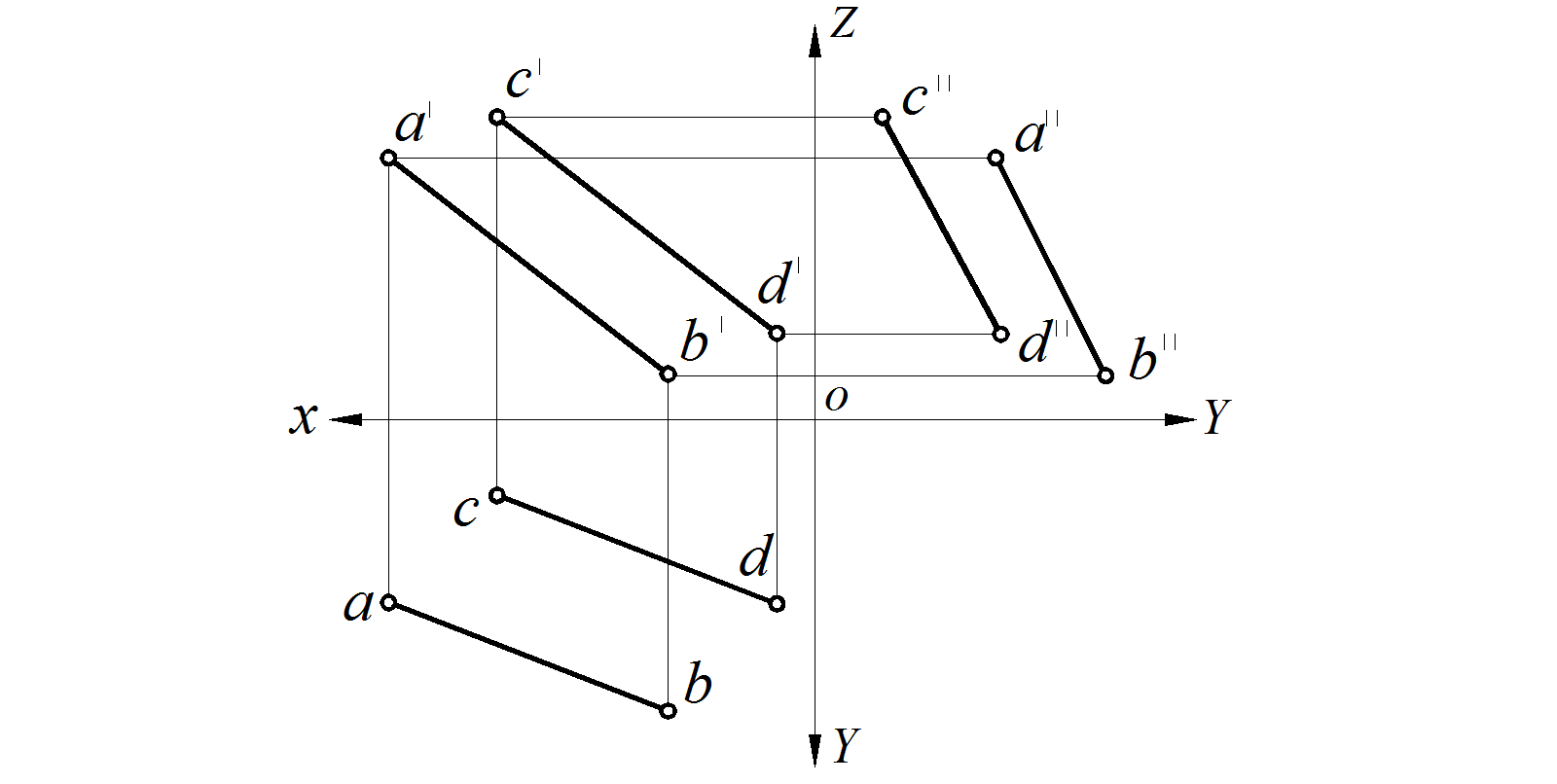
Рис. 31. Параллельные прямые АВ и С D
Скрещивающиеся прямые
Из курса средней школы известно, что скрещивающиеся прямые лежат в параллельных плоскостях, т. е. они в пространстве не пересекаются.
На чертеже проекции этих прямых могут пересекаться друг с другом, но, в отличие от чертежа пересекающихся прямых, точки пересечения одноименных проекций не лежат на одной линии связи.
Обычно на чертеже, изображающем скрещивающиеся прямые, определяют, какая из прямых находится выше или дальше другой от соответствующих плоскостей проекций, т. е. ближе к наблюдателю. В этом случае применяется метод конкурирующих (совпадающих) точек. Конкурирующие точки – это точки, лежащие на одном проецирующем луче.
На рис. 32 изображены проекции двух скрещивающихся прямых АВ и CD. На фронтальной проекции видим мнимое пересечение этих прямых, совпадающие точки 1 и 2 (1′ ≡ 2′), но, опуская из мнимой точки пересечения линию связи на горизонтальную проекцию, видно, что общей точки пересечения нет, а получаются две точки, принадлежащие этим прямым, лежащие на одной линии связи, но находящиеся в разных местах. И, судя по тому, что точка 1 находится дальше от оси Х, определяем по проекционной принадлежности, что прямая АВ находится дальше от фронтальной плоскости проекций, чем прямая CD. Точки 1 и 2 являются конкурирующими точками, при их совпадении принято невидимые (закрытые) точки заключать в скобки, поэтому точка 2, находящаяся за точкой 1, на фронтальной проекции заключена в скобки.
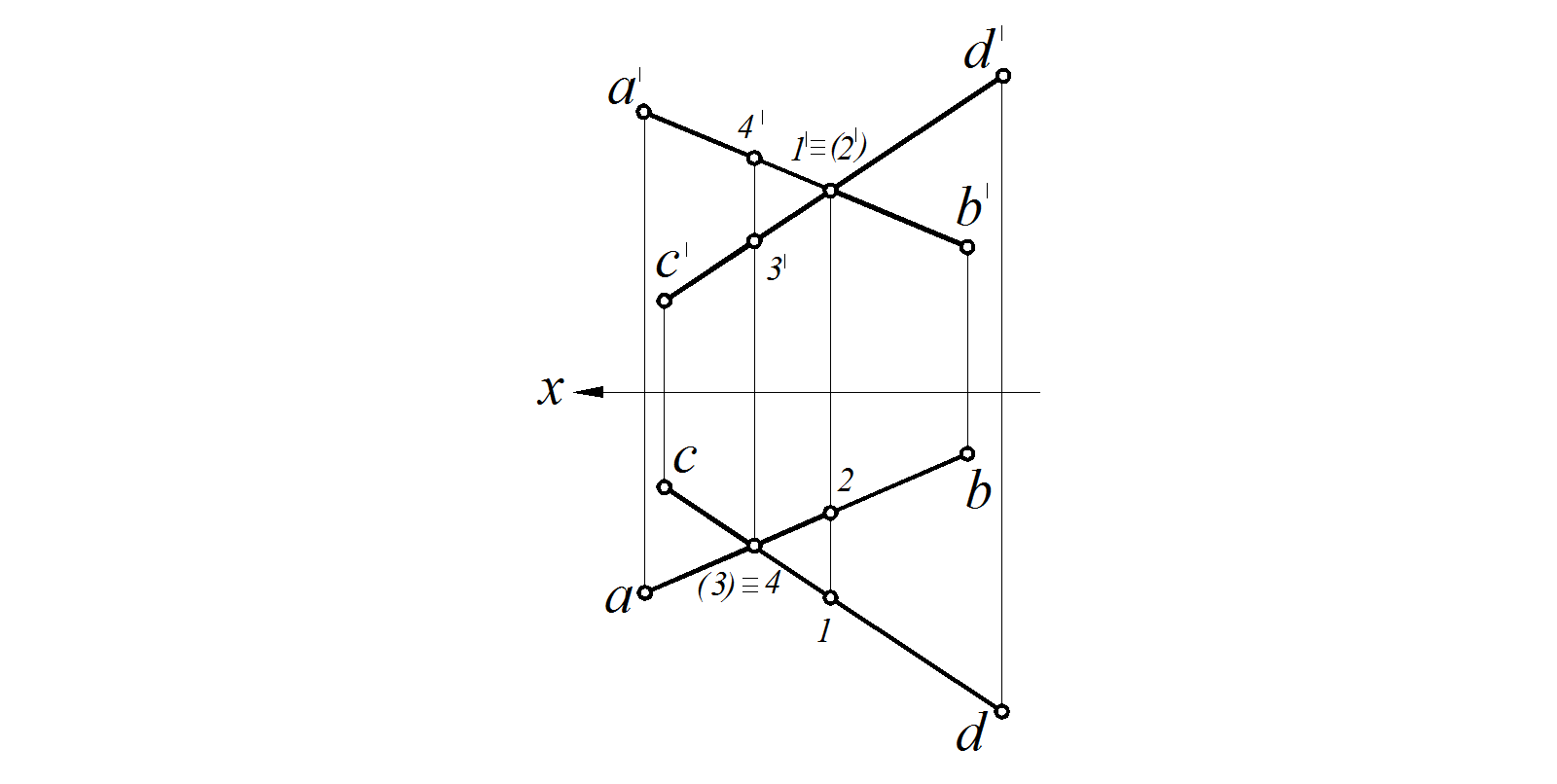
Рис. 32. Скрещивающиеся отрезки прямых АВ и С D:
точка 4 выше точки 3; точка 2 находится за точкой 1
Аналогичным образом можно рассматривать совпадающее положение точек 3 и 4 (3 ≡ 4) на горизонтальной плоскости проекций, представляющих мнимое пересечение проекций прямых АВ и CD. Далее, по проекционной принадлежности определив положение точек на фронтальной плоскости проекций, можно заключить, что точка 4 находится выше точки 3 и, значит, дальше от горизонтальной плоскости проекций. А так как точка 4 принадлежит прямой АВ, то и прямая АВ находится выше прямой CD.
Точка 3 находится ниже точки 4 и закрывается ею, поэтому ее горизонтальная проекция заключена в скобки, как невидимая.
Следует отметить, что для определения взаимного положения прямых общего положения достаточно рассмотреть их две любые проекции. Третью проекцию, без необходимости, строить необязательно.
Для определения взаимного положения прямых уровня одна из рассматриваемых проекций должна быть та, где прямая проецируется в натуральную величину.
Задача. Определить взаимное положение прямых А B и CD (рис. 33).
Решение
1. Анализируем заданный чертеж:
1.1. Взаимных положений прямых возможны 3 варианта: пересечение, параллельность и скрещивание. Так как заданные проекции прямых не параллельны друг другу, следовательно, заданные прямые не параллельны друг другу в пространстве.
1.2. Рассмотрим положение в пространстве каждой из заданных прямых. Прямая CD занимает общее положение. Прямая АВ занимает частное положение – является профильной прямой уровня. На профильной проекции прямая будет проецироваться в натуральную величину. Следовательно, для определения взаимного положения прямых АВ и CD надо построить профильные проекции этих прямых.
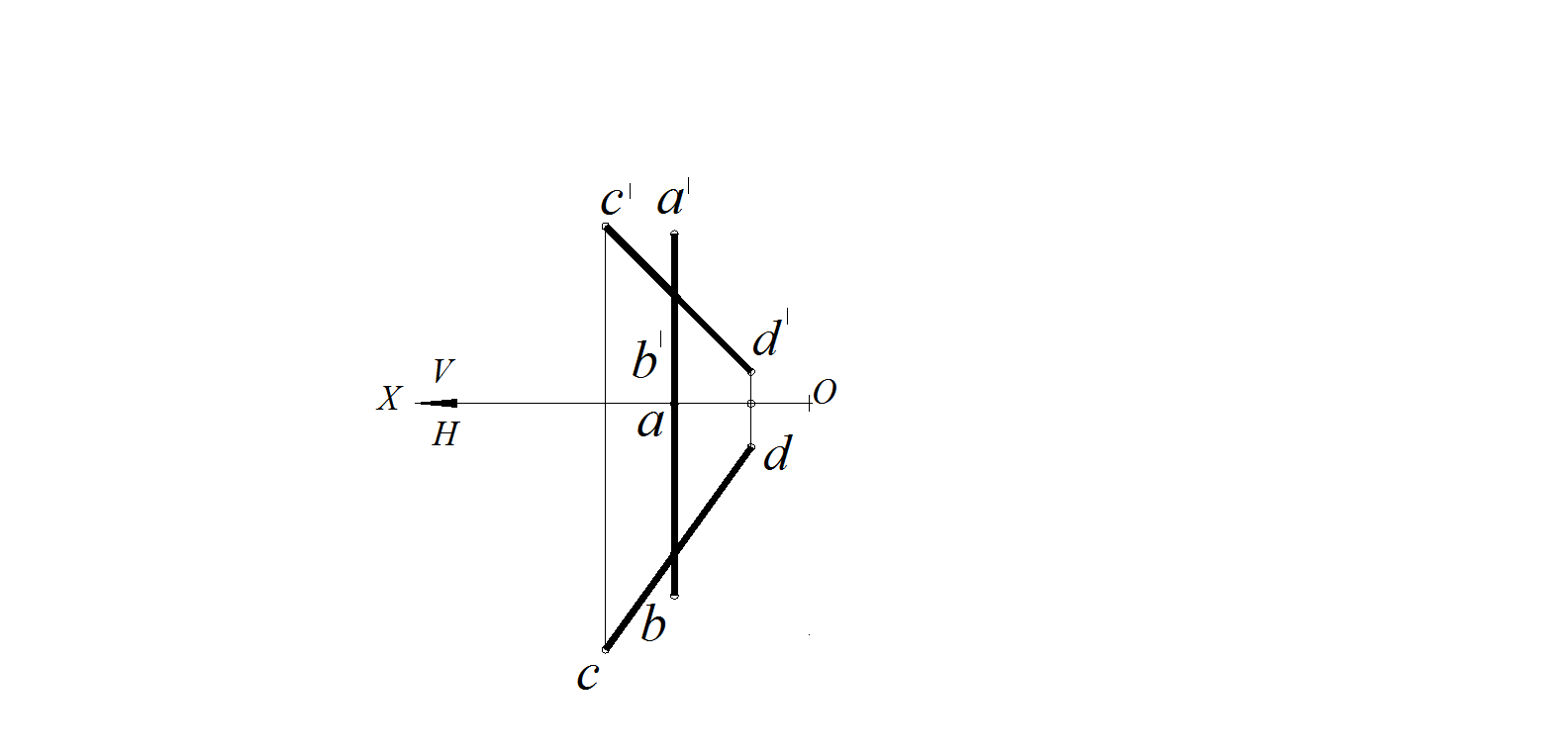
Рис. 33. Условие задачи
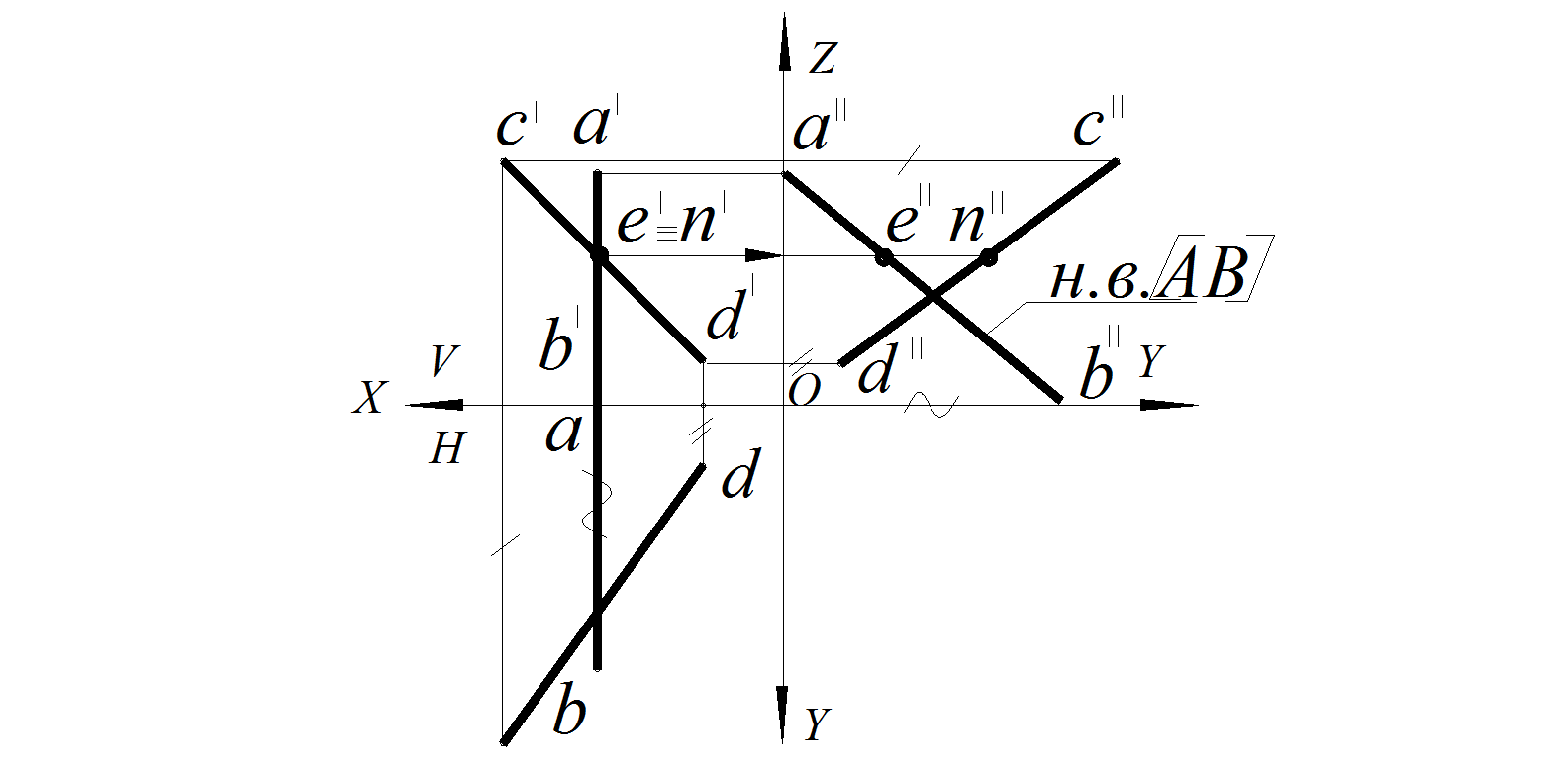
Рис. 34. Решение задачи
2. Как видно на рис. 34, мнимая точка пересечения прямых распадается на две точки на профильной проекции – Е и N. Следовательно, эти прямые скрещиваются.
Проекции плоских углов
Дата: 2018-11-18, просмотров: 1219.