Точка и прямая могут располагаться по-разному относительно друг друга и плоскостей проекций. На рис. 22–26 показаны случаи, в которых точка может принадлежать прямой, находится выше или ниже прямой, а также за или перед прямой.

Согласно свойству ортогонального проецирования, если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.

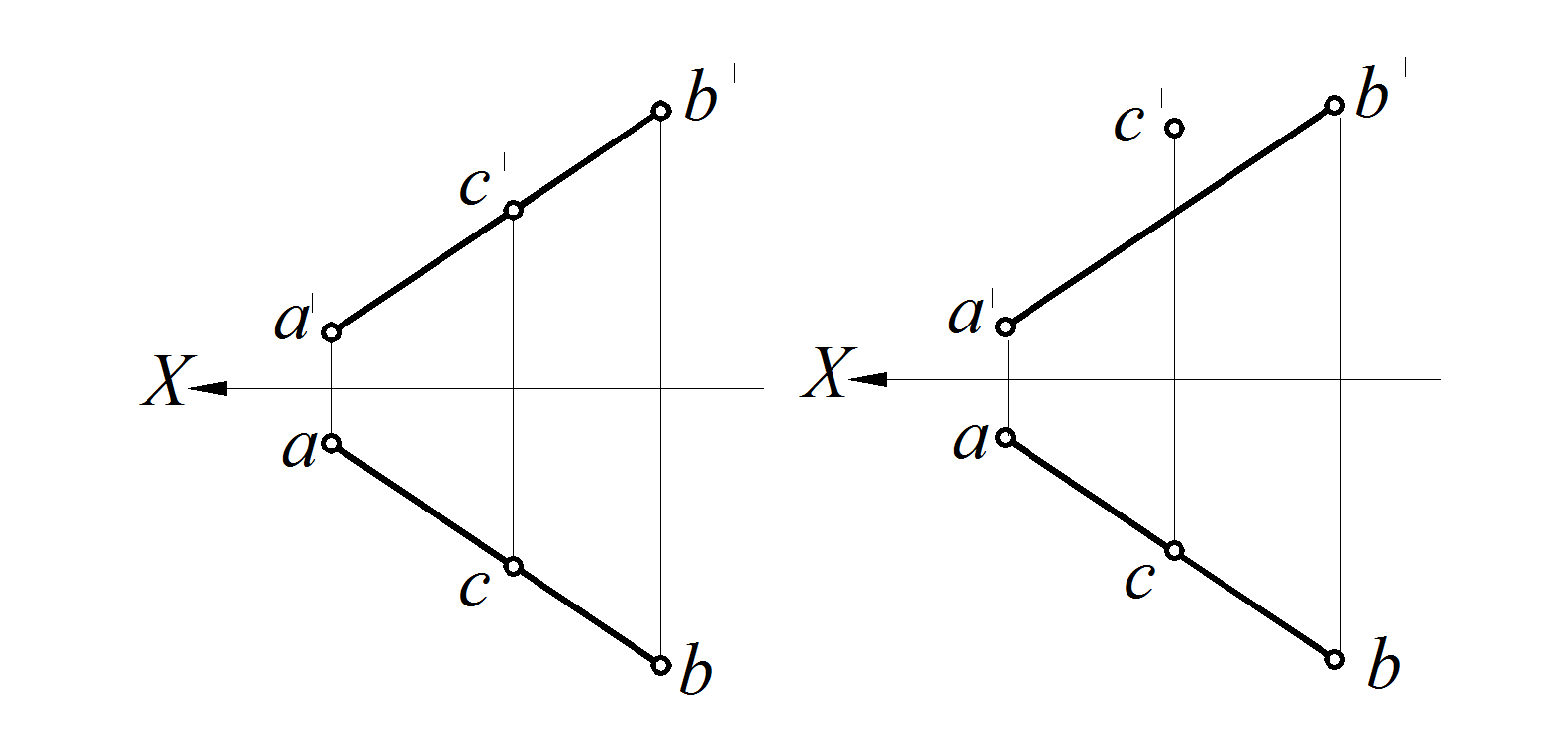
Рис. 22. Точка С принадлежит прямой АВ  Рис. 23. Точка С находится над прямой АВ

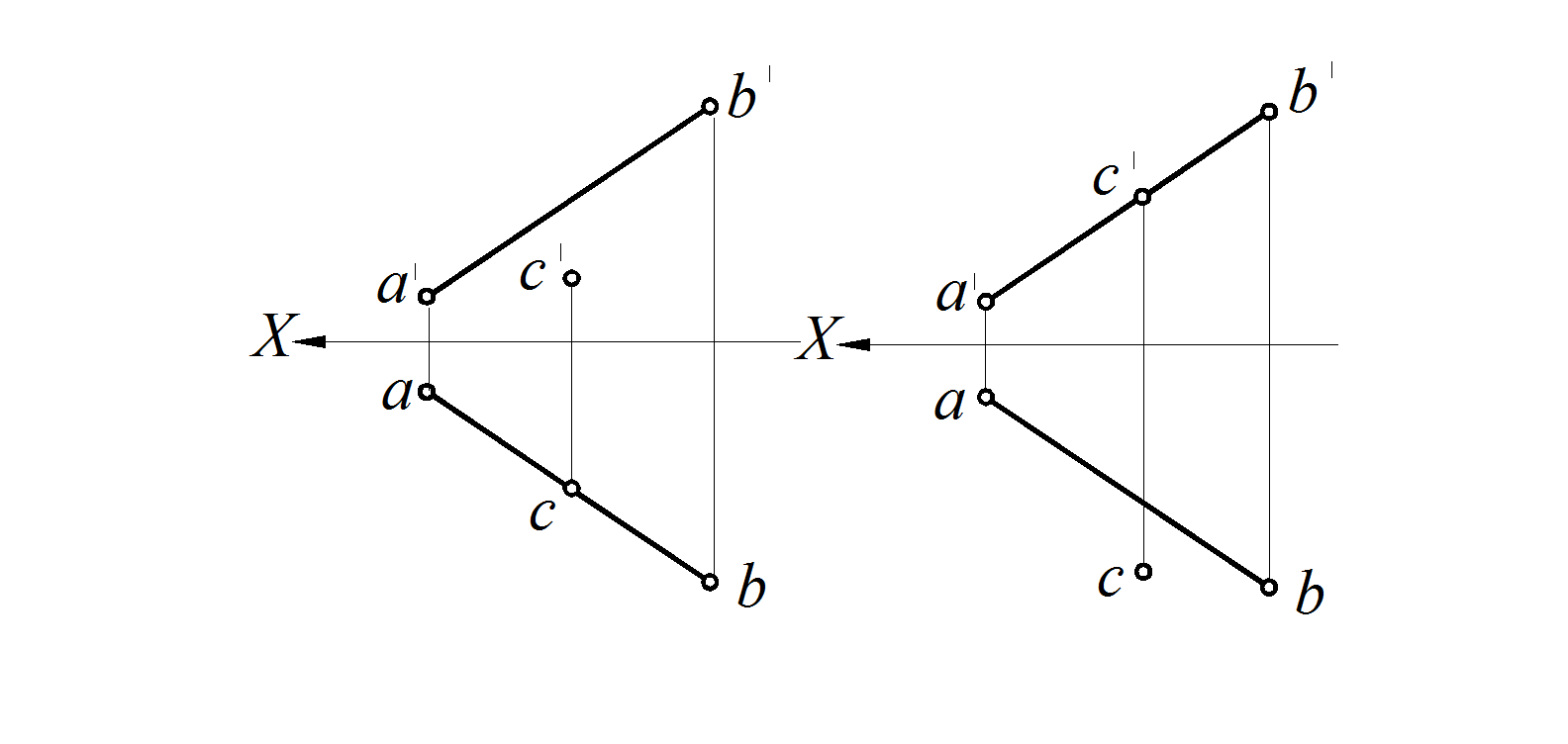
Рис. 24. Точка С находится ниже прямой АВ       Рис. 25. Точка С находится перед прямой АВ

Основные задачи на прямую

Деление отрезка в заданном отношении

Задача.

 На отрезке прямой АВ построить точку С, которая делит данный отрезок в отношении 2:3 от точки A (рис. 27).

Решение.

 Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекция этой точки делит одноименные проекции отрезка в том же отношении. Следовательно, чтобы разделить отрезок прямой в заданном отношении, достаточно разделить в этом же отношении одну из проекций данного отрезка.

Порядок выполнения графической части задачи:

1. Выбираем любую из проекций отрезка АВ, например, фронтальную – a ′ b ′.

2. Из точки b ′ проводим луч под любым углом к отрезку a ′ b ′. Так как отрезок АВ необходимо разделить в отношении 2:3, то равных частей на отрезке должно быть отложено 5 (2+3).

3. Задаемся произвольным единичным отрезком и откладываем от точки b ′ вдоль луча пять равных отрезков. Последнюю пятую точку обозначаем А_о и соединяем с точкой а′.

4. На отрезке |А_ob ′| отсчитываем от точки A_o два равных отрезка. Получаем точку С_о, которая делит отрезок А_оb ′ в отношении 2:3.

5. Параллельно отрезку |a ′А_о| через точку С_о проводим прямую. Получаем на отрезке a ′ b ′ точку с′, которая делит отрезок a ′ b ′ в отношении 2:3.

6. Горизонтальную проекцию точки С (с) находим по свойству принадлежности: проводим из точки с′ линию связи до пересечения с горизонтальной проекцией отрезка прямой АВ (а b ).

7. Построенная проекция точки С делит заданный отрезок прямой АВ в отношении 2:3.

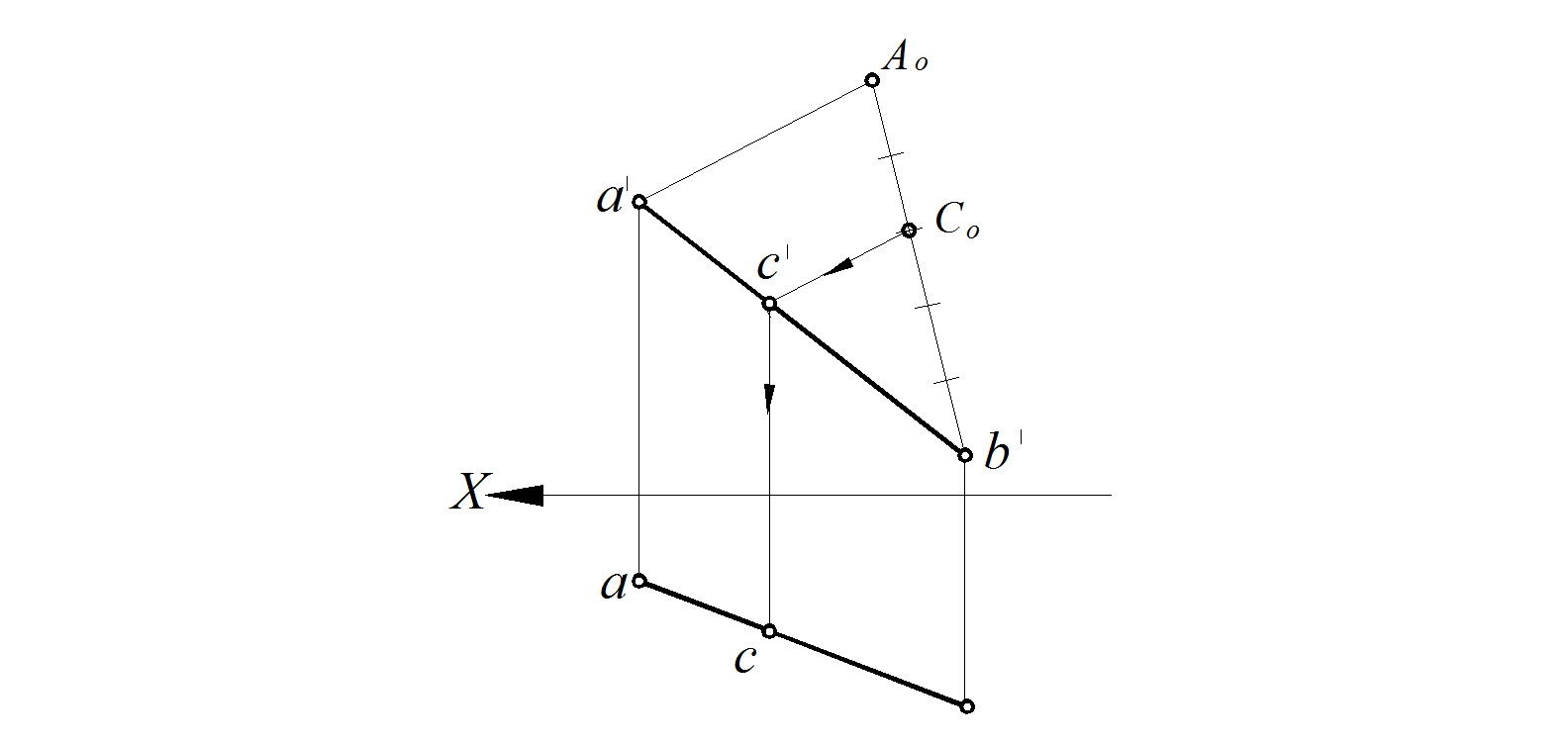
Рис. 27. Деление отрезка в заданном отношении

2. Определение натуральной величины отрезка прямой общего положения и определение углов наклона ее к плоскостям проекций

На плоскости проекций отрезок прямой общего положения проецируется с искажением. Для решения метрических задач необходимо определить натуральную величину отрезка прямой или угол наклона его к основным плоскостям проекций. Существует несколько методов определения натуральной величины отрезка прямой.