Плоскости проекций V, H, W принимаются за координатные плоскости, а оси проекций X, Y, Z за координатные оси как положительные, так и отрицательные (рис. 8).
Положение точки в пространстве задается тремя координатами – X, Y, Z. Проекции точки задаются двумя координатами: а(х, y), а′(х, z), а′′(y, z).
Зная направление для положительного и отрицательного значений координатных осей, принимая во внимание свойства проекций точки, можно построить проекции точки по координатам. Рассмотрим несколько задач на эту тему.
Задача.
Построить проекции точки А(–10; 40; –30) (рис. 8).
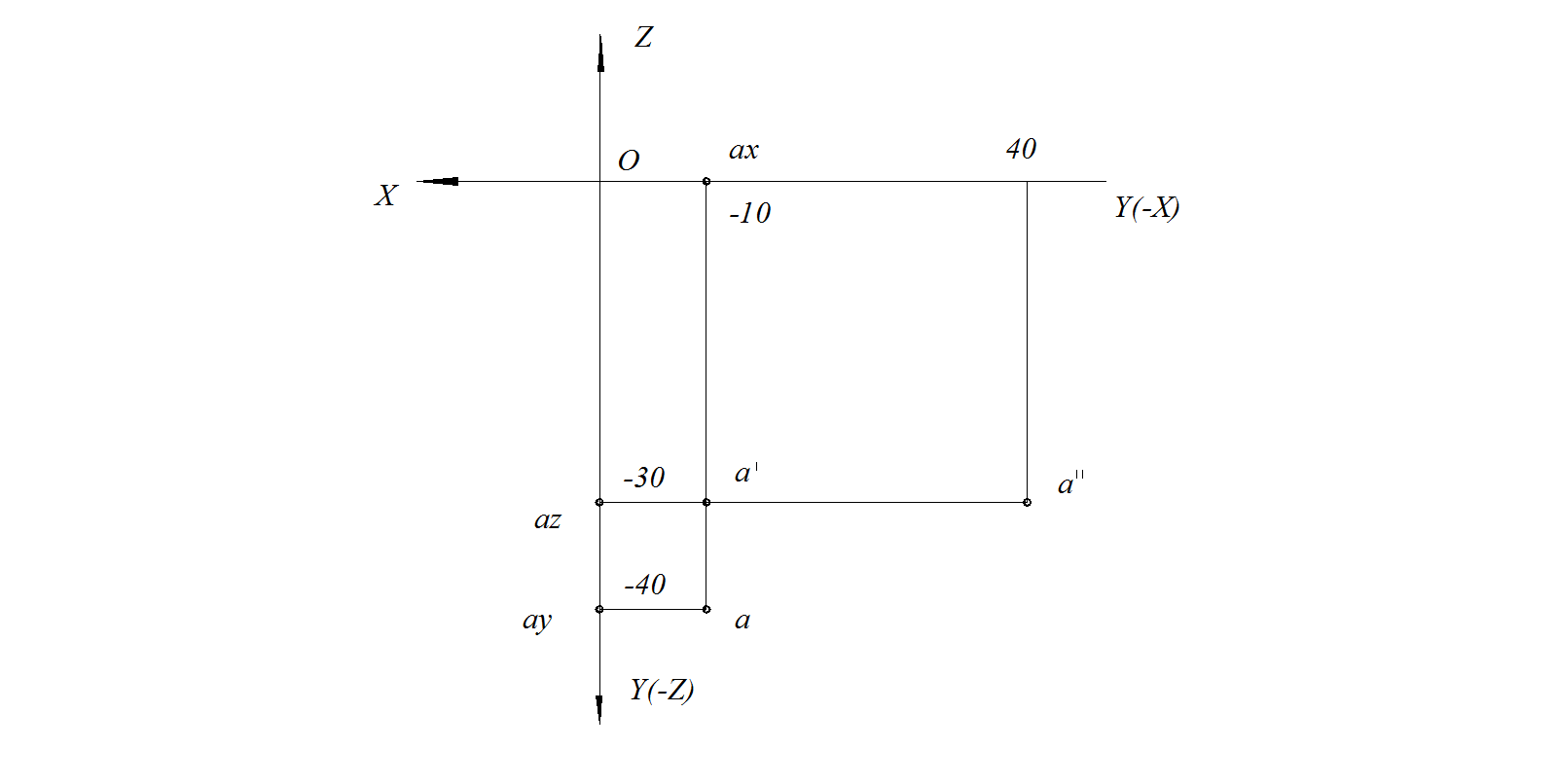
Рис. 8. Построение проекций точки А по координатам
Для построения фронтальной проекции а′ точки А справа от точки О на оси Х откладываем значение Х = –10. Вниз от точки О по направлению оси Z откладываем значение Z = –30. Пересечением перпендикуляров из точек а X и а Z, восстановленных к соответствующим осям Х и Z, определяем точку а′.
Для построения горизонтальной проекции а точки А по направлению оси Y вниз от точки О откладываем значение y = – 40. Через точку а Y проводим перпендикуляр до пересечения с линией связи а′а X. Отмечаем точку а – горизонтальную проекцию точки А. По расположению фронтальной и горизонтальной проекций точки А определяем, что точка А расположена в VΙΙΙ октанте.
Для построения профильной проекции а′′ точки А через ее фронтальную проекцию а′ проводим линию связи а′а Z и на ней, вправо от точки а Z, откладываем значение y = 40. Отмечаем точку а′′ – профильную проекцию точки А.
Вывод. Положение точки в пространстве вполне определено, если известны три ее координаты или две любые ортогональные проекции. Как следствие из этого – по двум любым заданным ортогональным проекциям точки можно всегда построить недостающую ее третью ортогональную проекцию.
Рассмотри построение точки по двум заданным ортогональным проекциям.
Задача.
По двум заданным ортогональным проекциям построить недостающую проекцию точки В (рис. 9).
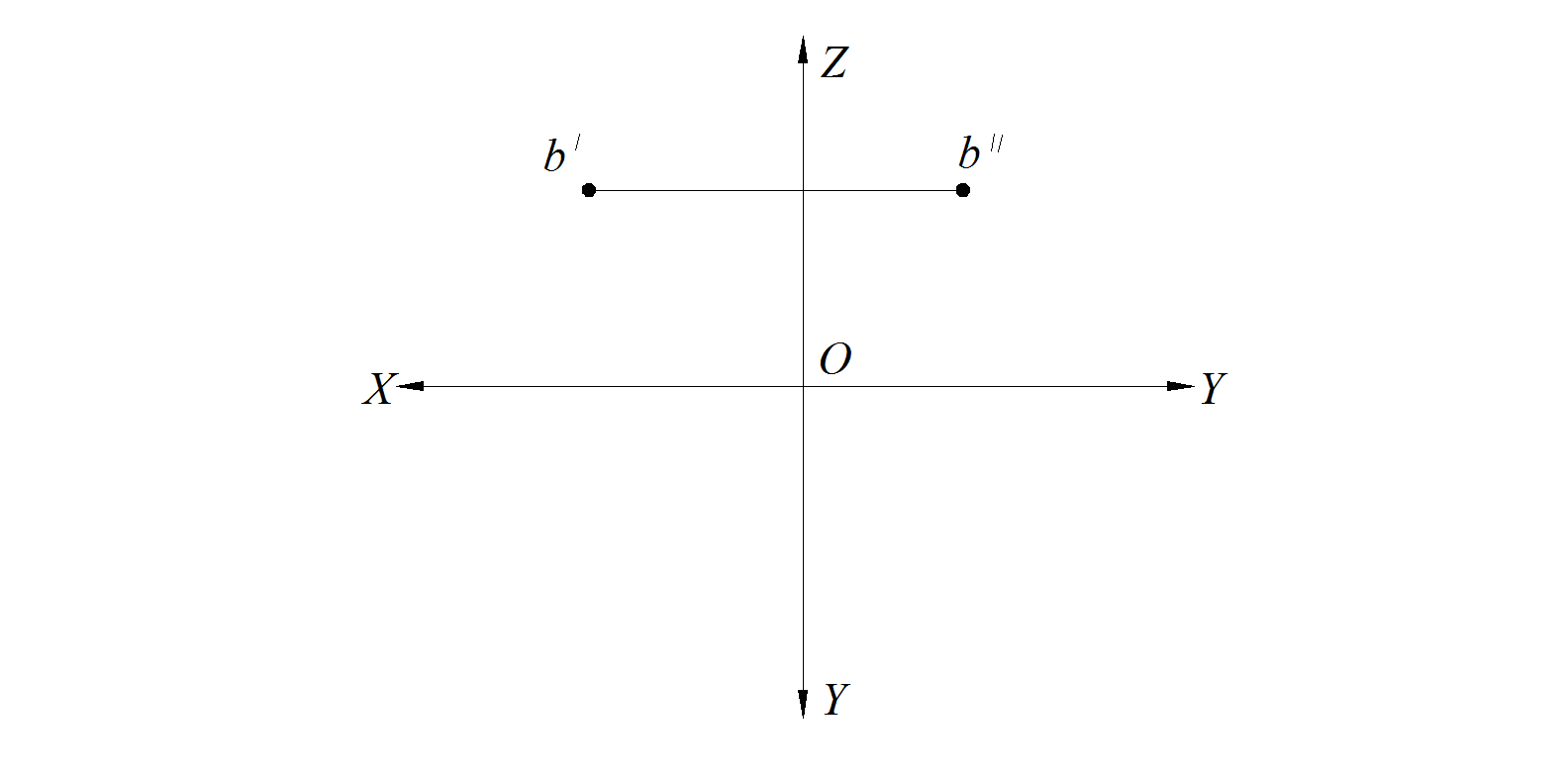
Рис. 9. Графическое условие задачи
Решение:
Анализируем графическое условие задачи: заданы фронтальная и профильная проекции точки В. Это значит, заданы все три координаты точки В. Следовательно, необходимо построить ее горизонтальную проекцию.
Порядок выполнения графической части задачи:
1. Для построения горизонтальной проекции точки В необходимо знать ХВ и УВ. Эти координаты находим на чертеже.
2. Замеряем УВ = bZ b ′′ и откладываем эту координату вдоль линии связи от оси ОХ от точки b Х .
3. Строим горизонтальную проекцию точки В (рис. 10).
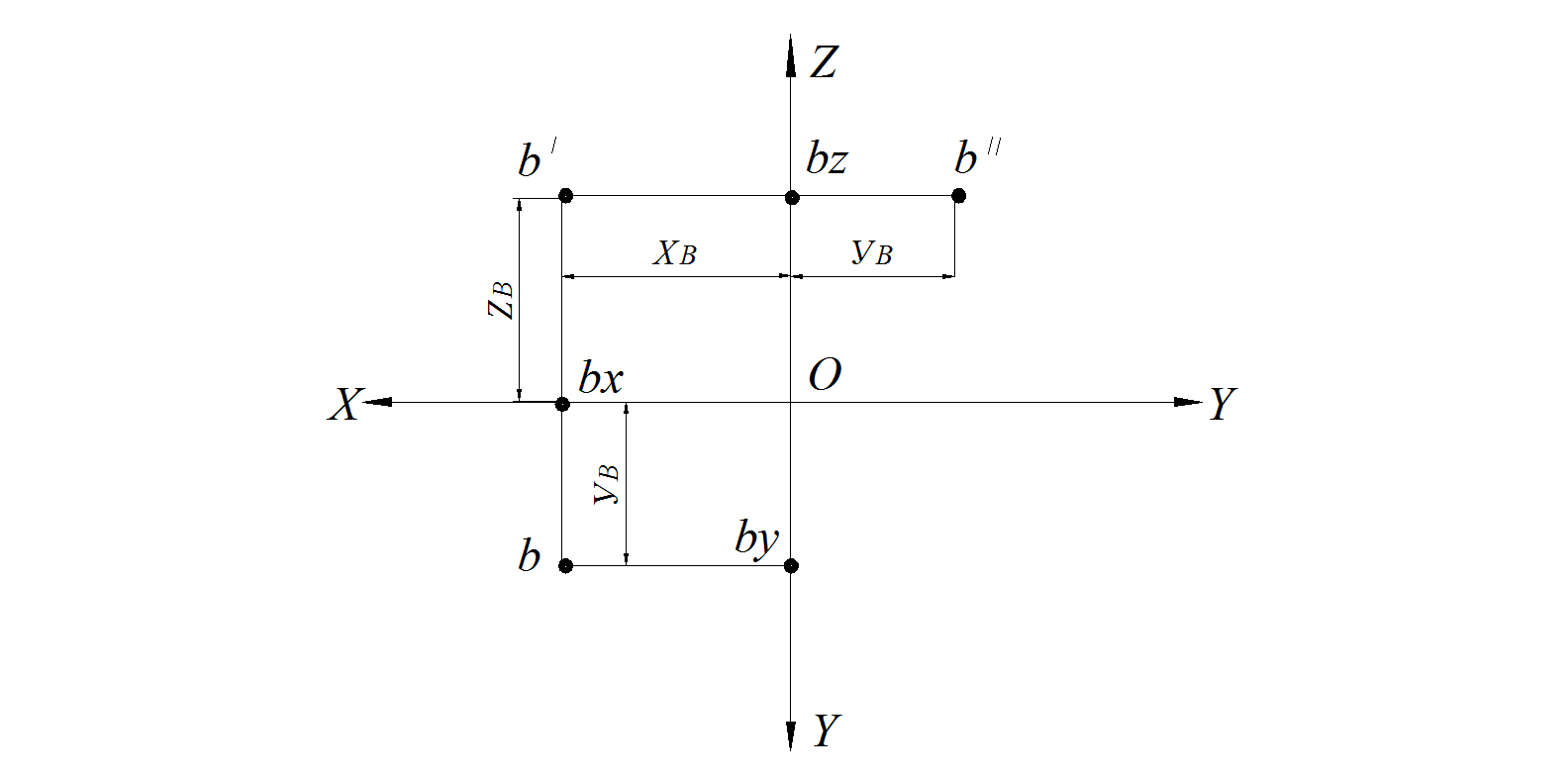
Рис. 10. Построение недостающей проекции
Прямая линия
Прямая линия – одно их основных понятий геометрии. Ее можно рассматривать как непрерывное однопараметрическое положение множества точек, следовательно, можно утверждать, что прямая линия бесконечна.
Прямая линия в линейной алгебре – линия первого порядка. Ее уравнение:
Ах + By + C = 0,
где А, В, С – любые постоянные.
Самый простой способ определения прямой в пространстве – найти две точки этой прямой. Соединив их, получим отрезок, вполне определяющий данную прямую. Для построения проекций прямой, строим проекции двух точек. Соединяем одноименные проекции точек. Получаем проекции отрезка данной прямой.
При ортогональном проецировании на плоскости проекций прямая линия проецируется в виде прямой. Чтобы построить проекции этой прямой линии, проходящей через заданные точки А и В, нужно построить проекции этих точек и провести прямые линии через их одноименные проекции (рис. 11). Получим:
аb – горизонтальную проекцию отрезка прямой;
а′b′ – фронтальную проекцию отрезка прямой.
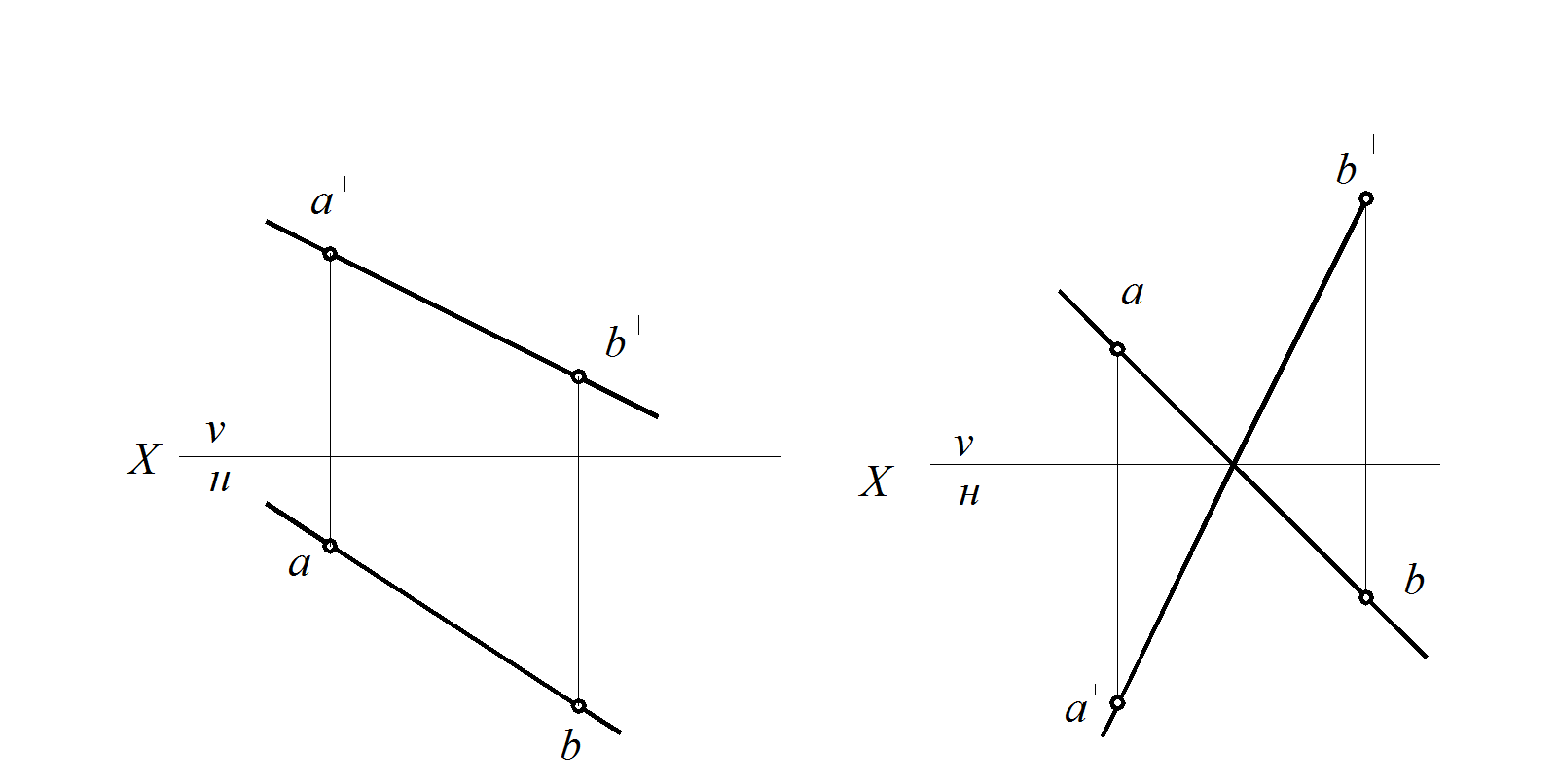
Рис. 11. Проекции отрезка прямой, проходящего через две точки
Следы прямой
Прямая пересекает плоскости проекций в точках, которые называются следами прямой.
Точка пересечения прямой N с горизонтальной плоскостью проекций Н (П1) называется горизонтальным следом N H .
Точка пересечения прямой с фронтальной плоскостью проекций V (П2) – фронтальным следом N V.
Точка пересечения прямой N с профильной плоскостью проекций W (П3) – профильным следом N W прямой.
Вывод:
· горизонтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в горизонтальной плоскости проекций H (П1);
· фронтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая во фронтальной плоскости проекций V (П2);
· профильный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в профильной плоскости проекций W (П3).
Задача.
Построить точки пересечения прямой N с горизонтальной Н (П1) и фронтальной V(П2) плоскостями проекций (рис. 12 а,б).
Анализируя задачу, приходим к выводу, что необходимо построить горизонтальный и фронтальный следы прямой.
Решение:
1. Построение фронтального следа N V .
Необходимо построить точку, принадлежащую прямой N и фронтальной плоскости проекций. Согласно изложенному ранее материалу, горизонтальная проекция искомой точки должна:
– лежать на оси Х;
– принадлежать горизонтальной проекции прямой N.
Порядок выполнения графической части задачи:
1.1. Отмечаем точку пересечения горизонтальной проекции n прямой N с осью Х, получаем точку n V – горизонтальную проекцию фронтального следа.
1.2. Через точку n V проводим линию связи перпендикулярно оси Х.
1.3. Находим точку пересечения линии связи с фронтальной проекцией n′ прямой N, получаем точку N V – фронтальную проекцию фронтального следа. Через эту точку прямая уходит во вторую четверть (рис. 12,а) и в третью четверть (рис. 12, б).
2. Построение горизонтального следа N H .
Необходимо построить точку, принадлежащую прямой N и горизонтальной плоскости проекций Н. Согласно изложенному ранее материалу, фронтальная проекция искомой точки должна:
– лежать на оси Х;
– принадлежать фронтальной проекции прямой N.
Порядок выполнения графической части задачи:
2.1. Отмечаем точку пересечения фронтальной проекции n′ прямой N с осью Х, получаем точку n H – фронтальную проекцию горизонтального следа.
2.2. Через точку n H проводим линию связи перпендикулярно оси Х.
2.3. Находим точку пересечения линии связи с горизонтальной проекцией n прямой N, получаем фронтальную проекцию фронтального следа. В этой точке прямая пересекает горизонтальную плоскость и уходит в четвертую четверть (рис. 12 а,б).
| а |
| б |
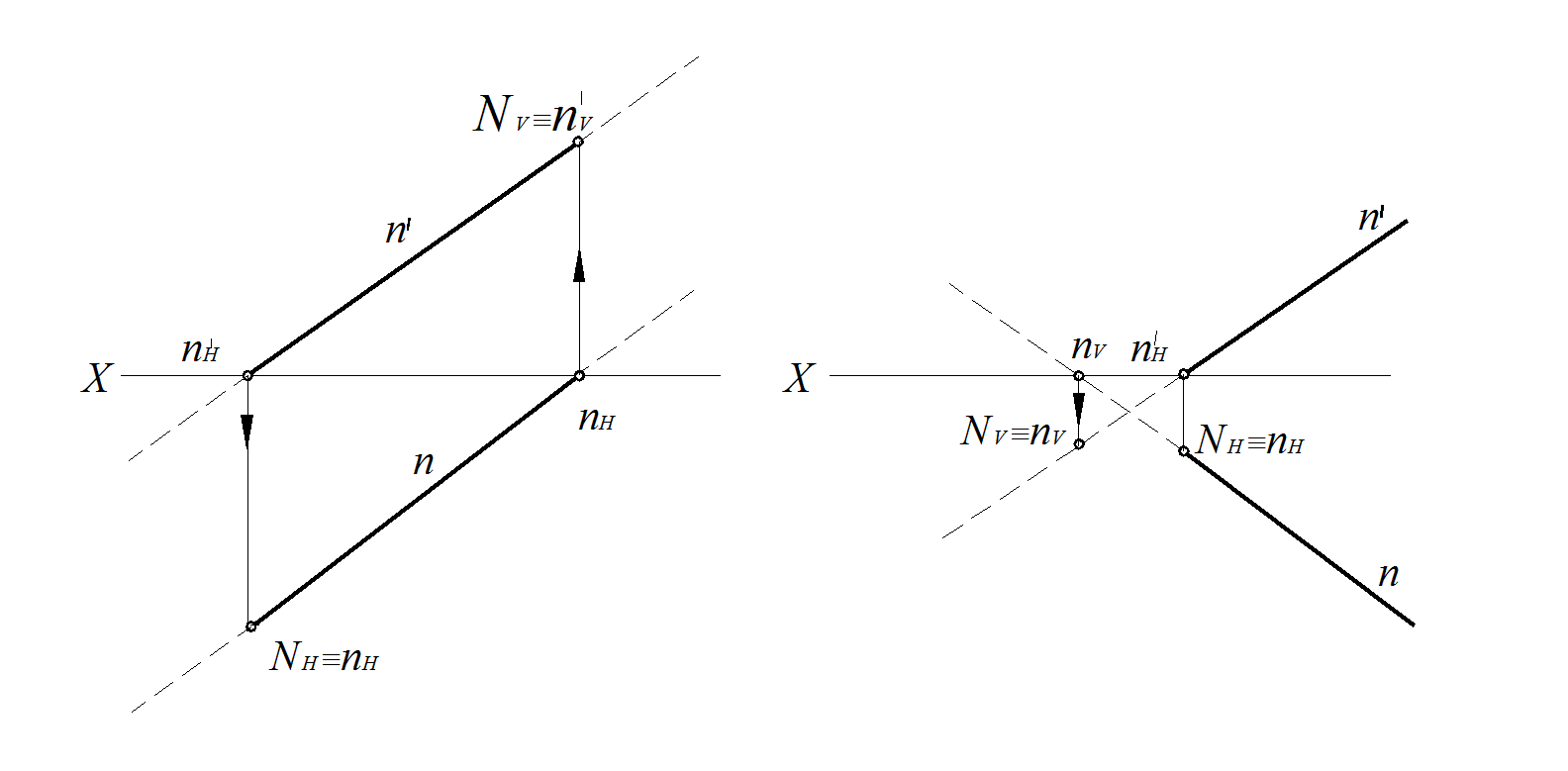
Рис. 12. Построение следов прямой линии N:
а – прямая уходит во вторую четверть; б – прямая уходит в третью четверть
Задача.
Построить горизонтальный и фронтальный следы прямой(рис. 13).
Решение:
1. Горизонтальный след прямой - это точка, лежащая одновременно на прямой АВ и в горизонтальной плоскости проекций. Следовательно, ее фронтальная проекция будет лежать на оси Х и на фронтальной проекции АВ. Продолжаем фронтальную проекцию прямой АВ до пересечения с осью Х. Полученная точка Сн будет горизонтальным следом прямой АВ.
2. Фронтальный след прямой - это точка, лежащая одновременно на прямой АВ и во фронтальной плоскости проекций. Следовательно, ее горизонтальная проекция будет лежать на оси Х и на горизонтальной проекции АВ. Продолжаем горизонтальную проекцию прямой АВ до пересечения с осью Х. Полученная точка С V будет фронтальным следом прямой АВ.
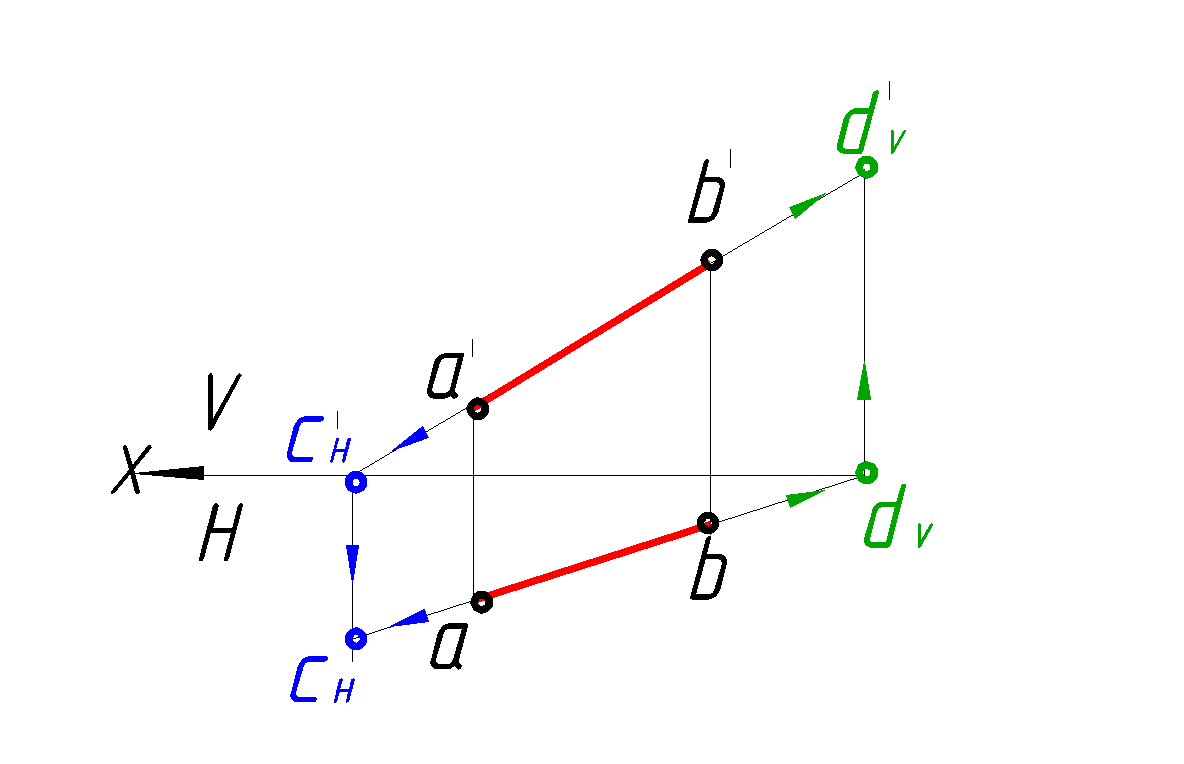
Рис. 13. Построение следов прямой линии АВ
Дата: 2018-11-18, просмотров: 1679.