ЧАСТЬ 1
Краткий курс лекций
Рекомендовано Учебно-методическим советом
Нижнетагильского технологического института (филиал) УрФУ
имени первого Президента России Б.Н.Ельцина
в качестве учебно-методического пособия для студентов всех форм обучения, всех направлений
/специальностей подготовки, изучающих дисциплину
«Инженерная и компьютерная графика»
Автор-составитель:
Л.Е. Аляутдинова
Нижний Тагил
2018
УДК 515(075.8)
ББК 22.15
Рецензенты:
Семенов В.А., Агропромышленный холдинг «Мираторг»,ЗАО «СК Короча», руководитель по развитию производства, канд. тех. наук
Федоров В.А., начальник бюро отдела главного энергетика АО «НПК «Уралвагонзавод»
Научный редактор: доц., д-р техн. наук Е.Н.Сафонов
Инженерная и компьютерная графика часть 1: краткий курс лекций / авт.-сост. Л. Е. Аляутдинова,; М-во образования и науки РФ ; ФГАОУ ВО «УрФУ им. первого Президента России Б.Н.Ельцина», Нижнетагил. технол. ин-т (фил.). – Нижний Тагил : НТИ (филиал) УрФУ, 2018. – 182 с.
Курс лекций представляет краткое изложение основных разделов начертательной геометрии, в которых рассмотрены теоретические основы проецирования, способы преобразования эпюра, образование поверхностей, методы построения линий их пересечения и развертывания. Теоретическая часть поясняется примерами задач с алгоритмом их решения.
.
Библиогр.: 6 назв. Рис. 134.
УДК 515(075.8)
ББК 22.15
Ó Аляутдинова Л. Е., составление, 2018
Оглавление
Введение................................................................................................... 4
1. метод проекций.ЭПЮР МОНЖА…………………………… .5
2. ТОЧКА.ПРЯМАЯ................................................................................... 12
3. ПЛОСКОСТЬ......................................................................................... 39
4. ПОЗИЦИОННЫЕ ЗАДАЧИ.................................................................. 62
5. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА..................................... 85
6. МНОГОГРАННИКИ………………………………………………………107
7. КРИВЫЕ ПОВЕРХНОСТИ………………………………………………122
8. ОБОЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ……………………………144
8.1.ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ ПЛОСКОСТЬЮ……144
8.2. ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ ПРЯМОЙ ЛИНИЕЙ..154
8.3.ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ................................................ 158
9. РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ....................................... 175
Библиографический список..................................................... 180
Введение
Начертательная геометрия – это первая часть дисциплины «Инженерная и компьютерная графика». Является одной из дисциплин, составляющих основу инженерного образования. Это раздел геометрии, в котором пространственные фигуры, представляющие совокупность точек, линий и поверхностей, изучаются по их проекционным отображениям, что позволяет представить форму предметов, их взаимное расположение в пространстве, определить их размеры, исследовать геометрические свойства.
Начертательная геометрия со времен ее основоположника
Гаспара Монжа (1746–1818) завоевала свое достойное место в высшей школе как наука. Важнейшее прикладное значение этой дисциплины состоит в том, что она учит владеть графическим языком, учит выполнять и читать чертежи и другие изображения геометрических объектов, без чего немыслимо формирование инженера.
Значение предмета начертательной геометрии определяется задачами, решаемыми этим курсом:
1) изучение методов и приемов построения изображений трехмерных объектов на плоскости чертежа – теория отображения пространства на плоскость;
2) изучение методов и приемов реконструкции трехмерных объектов по их плоским изображениям – теоретические основы чтения чертежа;
3) изучение методов и приемов решения метрических и позиционных задач на трехмерных объектах по их чертежам.
Успешное освоение этих задач начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления, что позволяет грамотно ставить и решать различные технические и технологические задачи в инженерной практике.
Настоящее издание представляет краткое изложение основных разделов курса начертательной геометрии, установленных рабочей программой, и рекомендуется совместно с другими учебными пособиями для самостоятельной работы студентов по изучению настоящего курса.
1. Метод проекций. ЭПЮР мОНЖА
Виды проецирования. Параллельные и ортогональные проекции. Свойства параллельных проекций. Понятие об эпюре Монжа и проекционном чертеже на три плоскости проекций.
В основе правил построения изображений лежит метод проекций. Суть метода заключается в том, что каждой точке трехмерного пространства соответствует определенная точка двухмерного пространства плоскости. Изучение его начинают с построений проекций точки, т. к. любой геометрический объект может рассматриваться как множество точек, заданных по определенному закону. Этот геометрический объект отображается на плоскость по закону проецирования. Процесс отображения называется проецированием. Результатом такого отображения является изображение объекта, которое называется проекцией.
Для построения проекции геометрического объекта задают аппарат проецирования, в который входит объект проецирования, например, точка А, и плоскость проецирования Р (иногда ее называют картинной плоскостью), не проходящая через точку А (рис. 1). Для получения изображения точки А на плоскость Р через нее проводят проецирующий луч до его пересечения с плоскостью Р в точке а. Полученную точку а называют проекцией точки А. Проекция (лат. projectio – выбрасывание вперед).
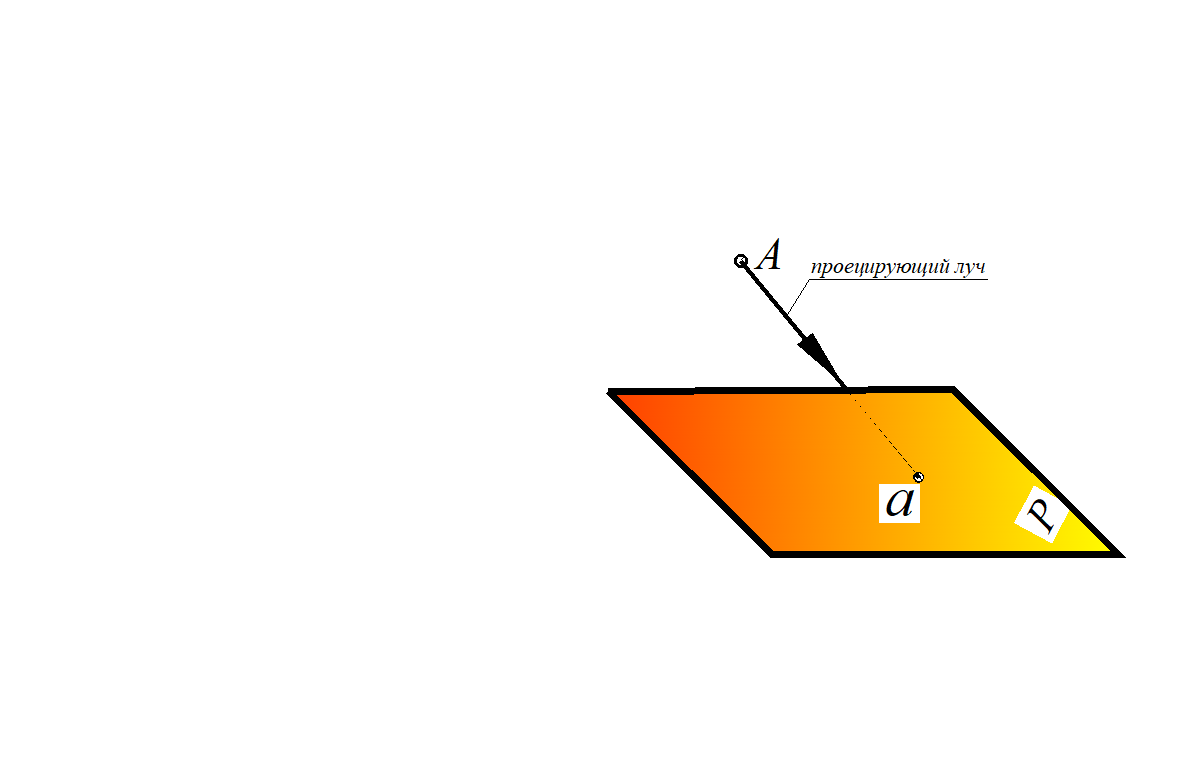
Рис. 1. Проецирование точки А
Виды проецирования
1. Центральное проецирование
Задан аппарат проецирования: центр проекций S, плоскость проецирования Р.
В результате центрального проецирования на плоскости Р получится центральная проекция любого геометрического объекта. На рис. 2 показано построение центральной проекции отрезка АВ. Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Таким образом получаем на плоскости перспективное изображение предмета или центральную проекцию.
Свойства центральных проекций:
– проекция точки – точка;
– проекция прямой – прямая;
– если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.
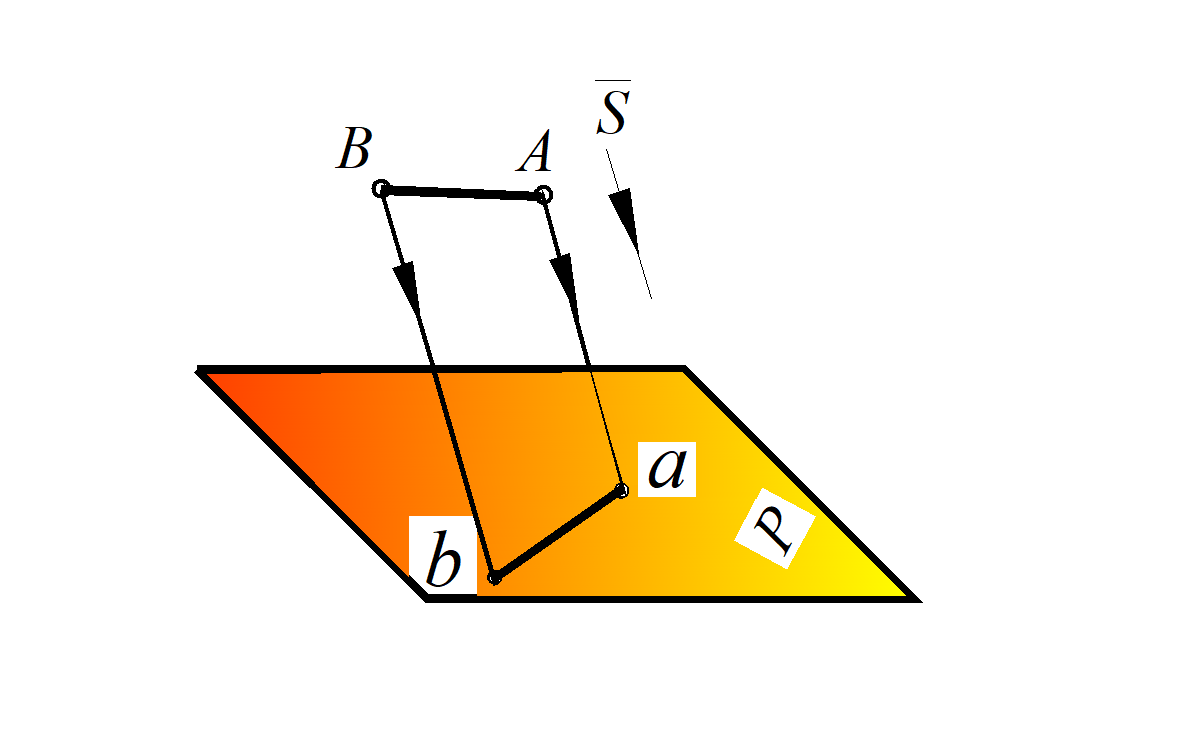
2. Параллельное проецирование – частный случай центрального проецирования, когда центр проецирования бесконечно удален. Поэтому в аппарат проецирования входит: направление проецирования S и плоскость проецирования Р. При этом проецирующие лучи рассматривают как прямые, параллельные между собой и параллельные заданному направлению проецирования S (рис. 3).
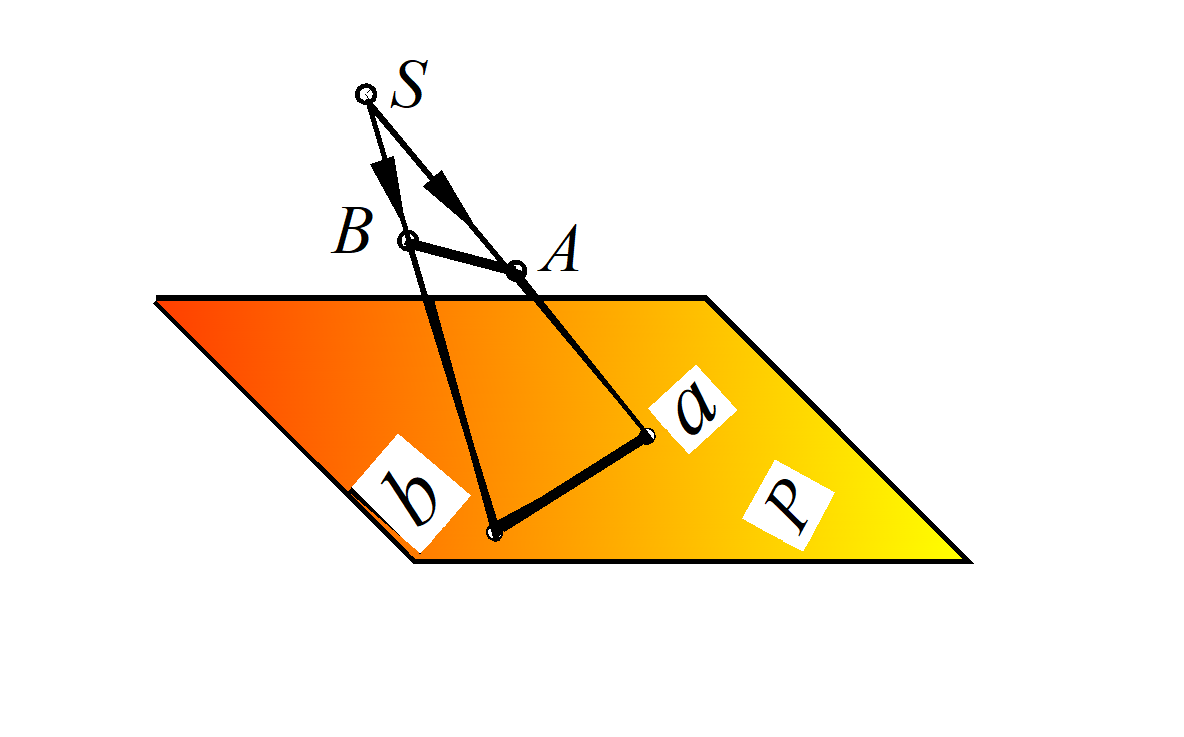
Рис. 2. Центральное проецирование отрезка АВ
| б |
| а |
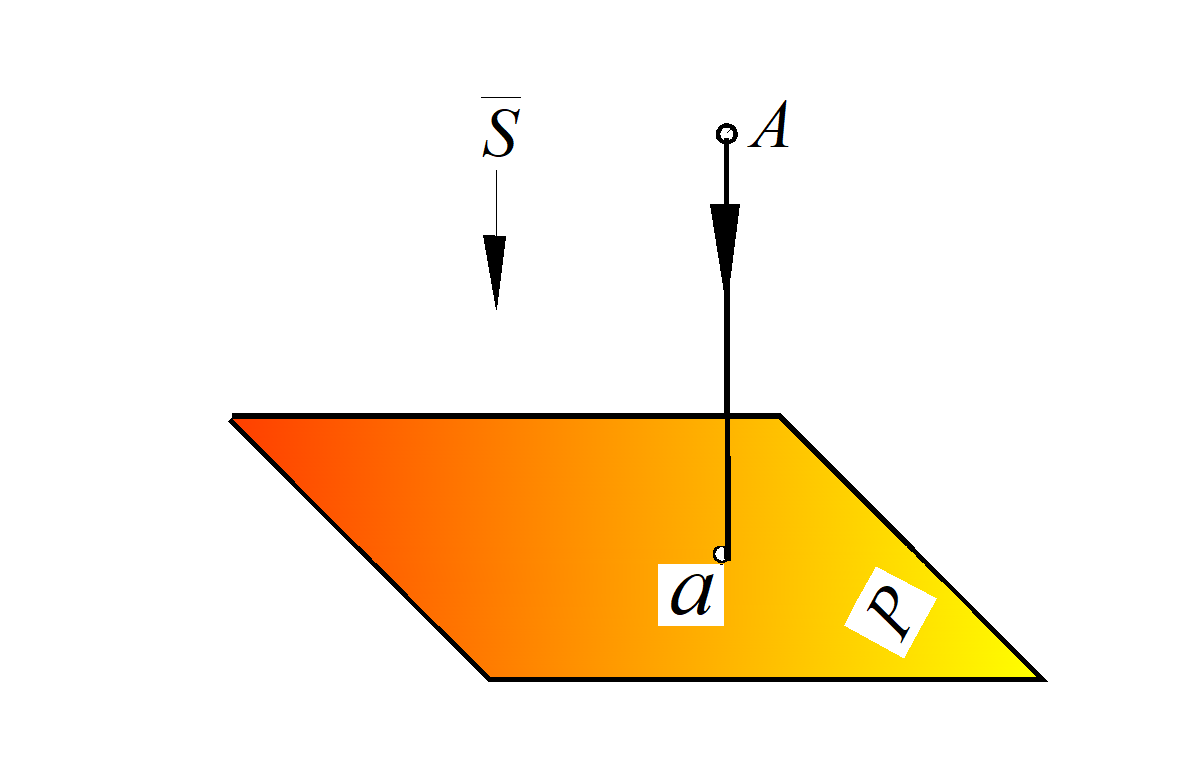
Рис. 3. Параллельное проецирование:
а – косоугольное отрезка АВ; б – ортогональное точки А
В зависимости от направления проецирования параллельные проекции могу быть:
– ортогональными (прямоугольными) проекциями – проекционные лучи падают перпендикулярно к картинной плоскости Р (рис. 3б);
– косоугольная проекция – проекционные лучи падают не перпендикулярно к картинной плоскости Р (рис. 3а).
Свойства параллельных проекций:
– проекция точки – точка;
– проекция прямой – прямая;
– если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой же прямой;
– проекции параллельных прямых параллельны;
– отношение отрезков прямой равно отношению их проекций.
Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием:
– простота построений изображения геометрического объекта;
– точность – сохранение точных форм и размеров проецируемой фигуры на чертеже;
– наглядность – чертеж должен создавать пространственное представление о форме геометрического объекта;
– обратимость – возможность восстановления оригинала по проекционным изображениям геометрического объекта.
Одна проекция точки не определяет положения ее в пространстве. Для этого требуются дополнительные условия. Изложенный французским геометром Г. Монжем в конце XVIII в. метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций обеспечил выразительность, точность и удобоизмеримость изображений предметов, был и остается основным методом составления технических чертежей.
Рассмотрим пространственную модель, состоящую из двух взаимно перпендикулярных плоскостей (рис. 1.4).
Фронтальная плоскость проекций V расположена вертикально.
Горизонтальная плоскость проекций Н расположена перпендикулярно фронтальной плоскости.
Проекционная ось х – линия пересечения плоскостей проекций.
Плоскости проекций образуют систему взаимно перпендикулярных плоскостей V / H и делят пространство на 4 четверти (4 двугранных угла).
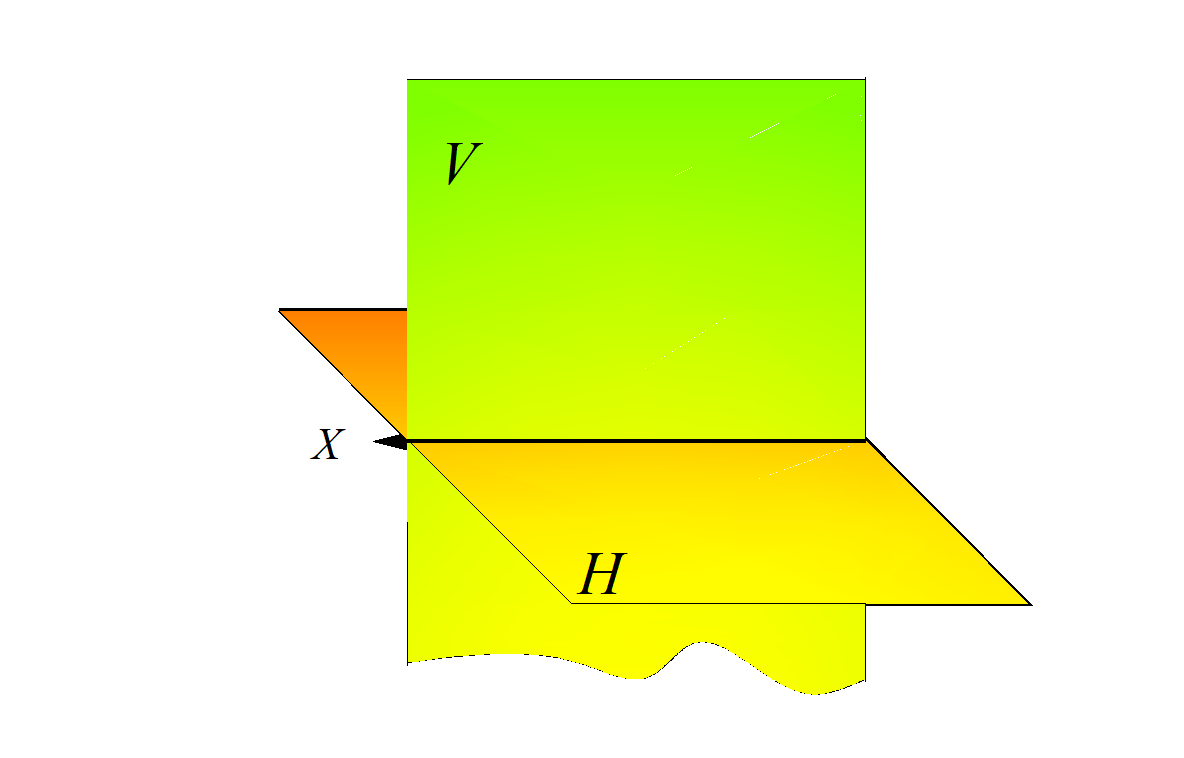
Рис. 4. Пространственная модель двух плоскостей проекций
Геометрический объект любой сложности можно рассматривать как множество точек, по взаимному расположению которых можно составить представление об объекте, а по расположению их относительно системы координат можно судить о положении его в пространстве.
Точка – основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования начинается с построения прямоугольных проекций точки.
При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. На рис. 5 показана точка А и ее ортогональные проекции а и а'. Справедливо и обратное, т. е. если на плоскостях проекций даны точки а и а' расположенные на прямых, пересекающих ось х в точке ах под прямым углом, то они являются проекцией некоторой точки А.
а – горизонтальная проекция точки А.
а' – фронтальная проекция точки.
Проекции точки всегда расположены на прямых, перпендикулярных оси х и пересекающих эту ось в одной и той же точке ах.
Две проекции точки вполне определяют ее положение относительно данной системы взаимно перпендикулярных плоскостей проекций.
а б
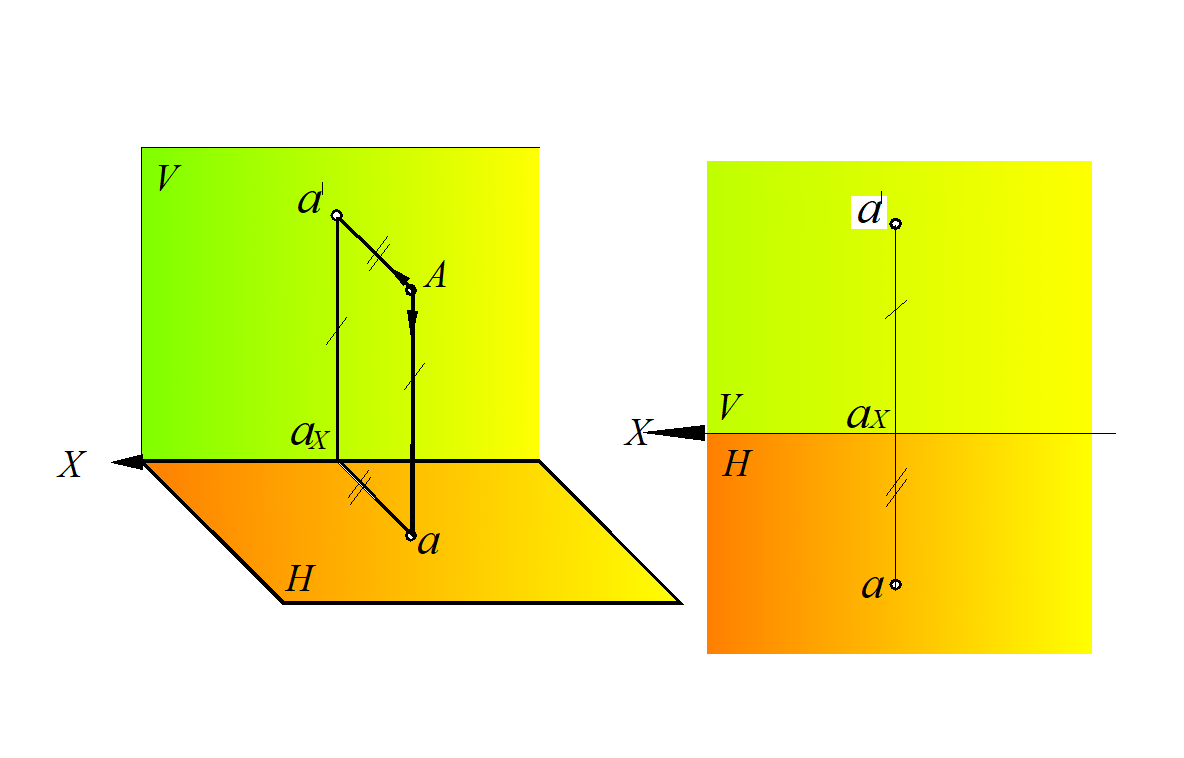
Рис. 5. Точка в системе двух плоскостей проекций:
а – модель; б,– эпюр
Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость Н совмещают вращением вокруг оси x с плоскостью V (рис. 1.5, б). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещены определенным образом одна с другой, называется эпюром (франц. Epure – чертеж.). Эпюр часто называют эпюром Монжа. Для упрощения эпюра границы плоскостей проекций не указывают (рис. 1.5, в).
На эпюре Монжа проекции а и а' окажутся расположенными на одном перпендикуляре к оси х. Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.
Дата: 2018-11-18, просмотров: 1157.