Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Нижнетагильский технологический институт (филиал)

 

 

ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА

ЧАСТЬ 1

Краткий курс лекций

 

 

Рекомендовано Учебно-методическим советом

Нижнетагильского технологического института (филиал) УрФУ

имени первого Президента России Б.Н.Ельцина

в качестве учебно-методического пособия для студентов всех форм обучения, всех направлений

/специальностей подготовки, изучающих дисциплину

«Инженерная и компьютерная графика»

 

 

Автор-составитель:

Л.Е. Аляутдинова

 

 

Нижний Тагил

2018

 

УДК 515(075.8)

ББК 22.15

 

Рецензенты:

Семенов В.А., Агропромышленный холдинг «Мираторг»,ЗАО «СК Короча», руководитель по развитию производства, канд. тех. наук

Федоров В.А., начальник бюро отдела главного энергетика АО «НПК «Уралвагонзавод»

Научный редактор: доц., д-р техн. наук Е.Н.Сафонов

Инженерная и компьютерная графика часть 1: краткий курс лекций / авт.-сост. Л. Е. Аляутдинова,; М-во образования и науки РФ ; ФГАОУ ВО «УрФУ им. первого Президента России Б.Н.Ельцина», Нижнетагил. технол. ин-т (фил.). – Нижний Тагил : НТИ (филиал) УрФУ, 2018. – 182 с.

 

Курс лекций представляет краткое изложение основных разделов начертательной геометрии, в которых рассмотрены теоретические основы проецирования, способы преобразования эпюра, образование поверхностей, методы построения линий их пересечения и развертывания. Теоретическая часть поясняется примерами задач с алгоритмом их решения.

.

 

 

Библиогр.: 6 назв. Рис. 134.

 

 

УДК 515(075.8)

ББК 22.15

 

Ó Аляутдинова Л. Е., составление, 2018

 

Оглавление

Введение................................................................................................... 4

1. метод проекций.ЭПЮР МОНЖА……………………………       .5

2. ТОЧКА.ПРЯМАЯ................................................................................... 12

 3. ПЛОСКОСТЬ......................................................................................... 39

4. ПОЗИЦИОННЫЕ ЗАДАЧИ.................................................................. 62

 5. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА..................................... 85

 6. МНОГОГРАННИКИ………………………………………………………107

 7. КРИВЫЕ ПОВЕРХНОСТИ………………………………………………122

 8. ОБОЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ……………………………144

 8.1.ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ ПЛОСКОСТЬЮ……144

 8.2. ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ ПРЯМОЙ ЛИНИЕЙ..154

8.3.ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ................................................ 158

9. РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ....................................... 175

Библиографический список..................................................... 180

 

Введение

 

Начертательная геометрия – это первая часть дисциплины «Инженерная и компьютерная графика». Является одной из дисциплин, составляющих основу инженерного образования. Это раздел геометрии, в котором пространственные фигуры, представляющие совокупность точек, линий и поверхностей, изучаются по их проекционным отображениям, что позволяет представить форму предметов, их взаимное расположение в пространстве, определить их размеры, исследовать геометрические свойства.

Начертательная геометрия со времен ее основоположника
Гаспара Монжа (1746–1818) завоевала свое достойное место в высшей школе как наука. Важнейшее прикладное значение этой дисциплины состоит в том, что она учит владеть графическим языком, учит выполнять и читать чертежи и другие изображения геометрических объектов, без чего немыслимо формирование инженера.

Значение предмета начертательной геометрии определяется задачами, решаемыми этим курсом:

1)  изучение методов и приемов построения изображений трехмерных объектов на плоскости чертежа – теория отображения пространства на плоскость;

2)  изучение методов и приемов реконструкции трехмерных объектов по их плоским изображениям – теоретические основы чтения чертежа;

3)  изучение методов и приемов решения метрических и позиционных задач на трехмерных объектах по их чертежам.

Успешное освоение этих задач начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления, что позволяет грамотно ставить и решать различные технические и технологические задачи в инженерной практике.

Настоящее издание представляет краткое изложение основных разделов курса начертательной геометрии, установленных рабочей программой, и рекомендуется совместно с другими учебными пособиями для самостоятельной работы студентов по изучению настоящего курса.

 

1. Метод проекций. ЭПЮР мОНЖА

 

Виды проецирования. Параллельные и ортогональные проекции. Свойства параллельных проекций. Понятие об эпюре Монжа и проекционном чертеже на три плоскости проекций.

В основе правил построения изображений лежит метод проекций. Суть метода заключается в том, что каждой точке трехмерного пространства соответствует определенная точка двухмерного пространства плоскости. Изучение его начинают с построений проекций точки, т. к. любой геометрический объект может рассматриваться как множество точек, заданных по определенному закону. Этот геометрический объект отображается на плоскость по закону проецирования. Процесс отображения называется проецированием. Результатом такого отображения является изображение объекта, которое называется проекцией.

Для построения проекции геометрического объекта задают аппарат проецирования, в который входит объект проецирования, например, точка А, и плоскость проецирования Р (иногда ее называют картинной плоскостью), не проходящая через точку А (рис. 1). Для получения изображения точки А на плоскость Р через нее проводят проецирующий луч до его пересечения с плоскостью Р в точке а. Полученную точку а называют проекцией точки А. Проекция (лат. projectio – выбрасывание вперед).

 

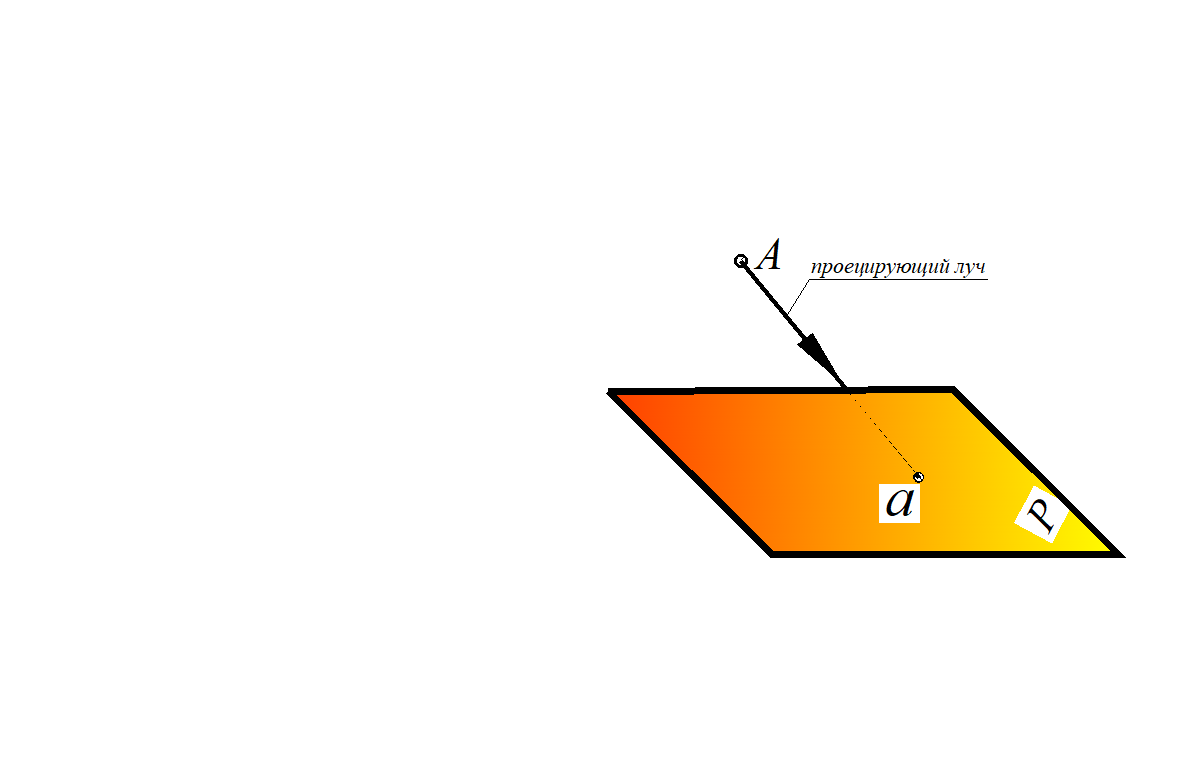
Рис. 1. Проецирование точки А

Виды проецирования

1. Центральное проецирование

Задан аппарат проецирования: центр проекций S, плоскость проецирования Р.

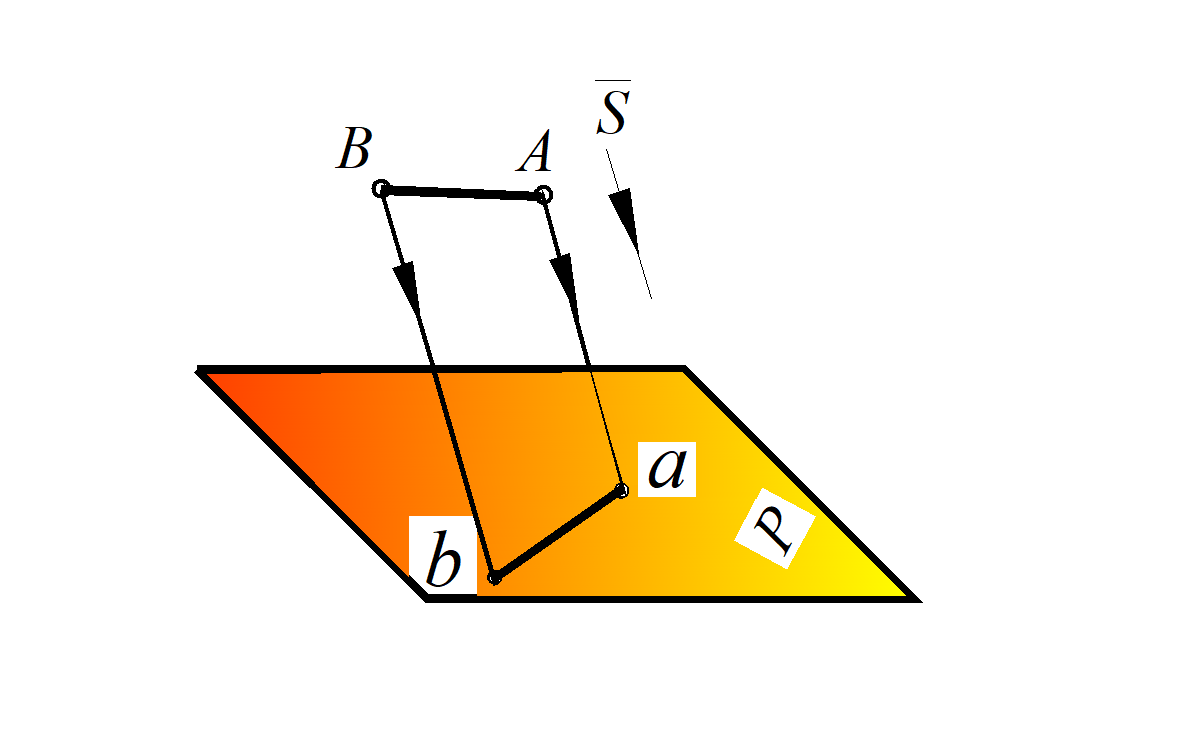
В результате центрального проецирования на плоскости Р получится центральная проекция любого геометрического объекта. На рис. 2 показано построение центральной проекции отрезка АВ. Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Таким образом получаем на плоскости перспективное изображение предмета или центральную проекцию.

Свойства центральных проекций:

– проекция точки – точка;

– проекция прямой – прямая;

– если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

2. Параллельное проецирование – частный случай центрального проецирования, когда центр проецирования бесконечно удален. Поэтому в аппарат проецирования входит: направление проецирования S и плоскость проецирования Р. При этом проецирующие лучи рассматривают как прямые, параллельные между собой и параллельные заданному направлению проецирования S (рис. 3).

 

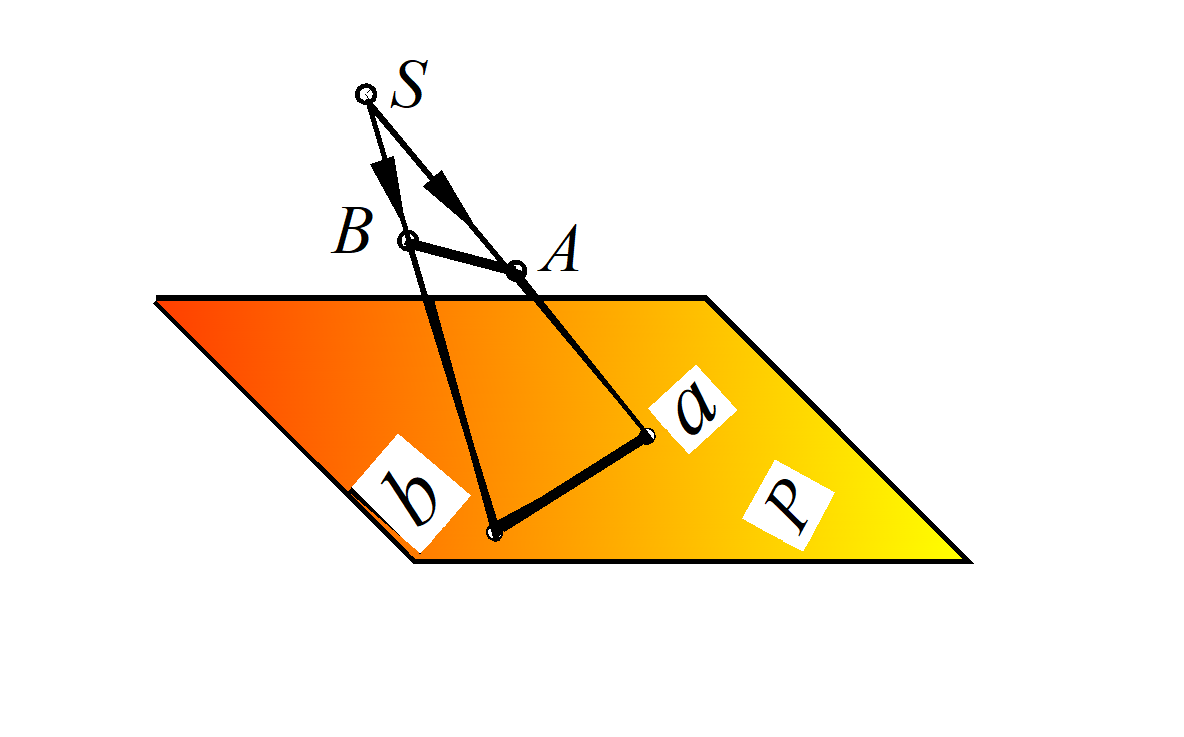
Рис. 2. Центральное проецирование отрезка АВ

                                                              

б

а

 

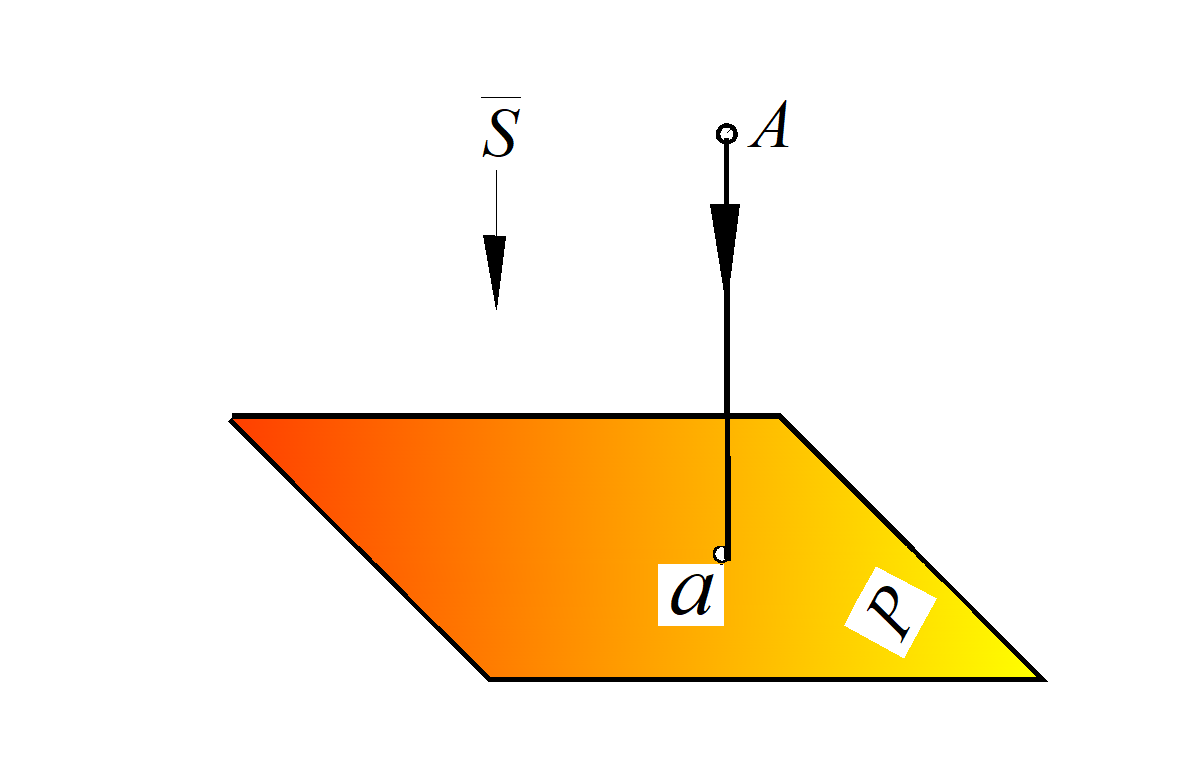
Рис. 3. Параллельное проецирование:

 а – косоугольное отрезка АВ; б – ортогональное точки А

 

В зависимости от направления проецирования параллельные проекции могу быть:

– ортогональными (прямоугольными) проекциями – проекционные лучи падают перпендикулярно к картинной плоскости Р (рис. 3б);

– косоугольная проекция – проекционные лучи падают не перпендикулярно к картинной плоскости Р (рис. 3а).

Свойства параллельных проекций:

– проекция точки – точка;

– проекция прямой – прямая;

– если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой же прямой;

 – проекции параллельных прямых параллельны;

 – отношение отрезков прямой равно отношению их проекций.

Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием:

– простота построений изображения геометрического объекта;

– точность – сохранение точных форм и размеров проецируемой фигуры на чертеже;

– наглядность – чертеж должен создавать пространственное представление о форме геометрического объекта;

– обратимость – возможность восстановления оригинала по проекционным изображениям геометрического объекта.

Одна проекция точки не определяет положения ее в пространстве. Для этого требуются дополнительные условия. Изложенный французским геометром Г. Монжем в конце XVIII в. метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций обеспечил выразительность, точность и удобоизмеримость изображений предметов, был и остается основным методом составления технических чертежей.

Рассмотрим пространственную модель, состоящую из двух взаимно перпендикулярных плоскостей (рис. 1.4).

Фронтальная плоскость проекций V расположена вертикально.

Горизонтальная плоскость проекций Н расположена перпендикулярно фронтальной плоскости.

Проекционная ось х – линия пересечения плоскостей проекций.

Плоскости проекций образуют систему взаимно перпендикулярных плоскостей V / H и делят пространство на 4 четверти (4 двугранных угла).

 

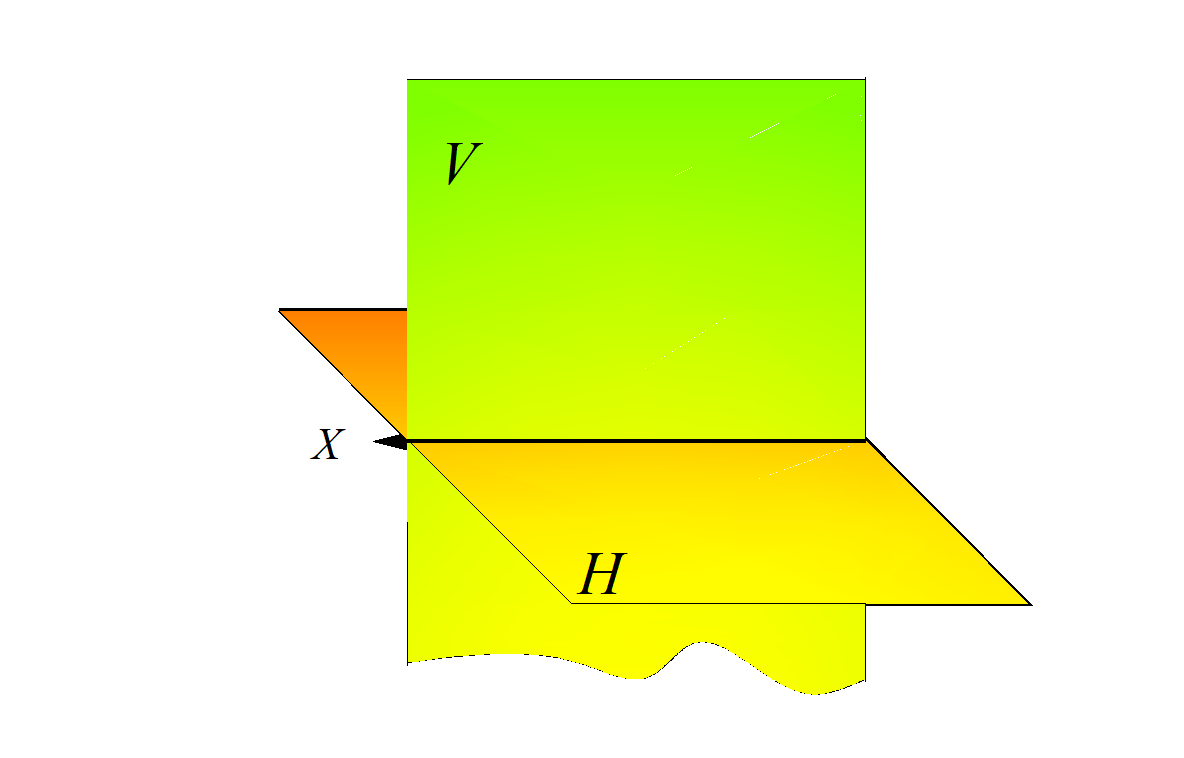
Рис. 4. Пространственная модель двух плоскостей проекций

 

Геометрический объект любой сложности можно рассматривать как множество точек, по взаимному расположению которых можно составить представление об объекте, а по расположению их относительно системы координат можно судить о положении его в пространстве.

Точка – основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования начинается с построения прямоугольных проекций точки.

При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. На рис. 5 показана точка А и ее ортогональные проекции а и а'. Справедливо и обратное, т. е. если на плоскостях проекций даны точки а и а' расположенные на прямых, пересекающих ось х в точке а_х под прямым углом, то они являются проекцией некоторой точки А.

а – горизонтальная проекция точки А.

а' – фронтальная проекция точки.

Проекции точки всегда расположены на прямых, перпендикулярных оси х и пересекающих эту ось в одной и той же точке а_х.

Две проекции точки вполне определяют ее положение относительно данной системы взаимно перпендикулярных плоскостей проекций.

               а                                                               б                                

 

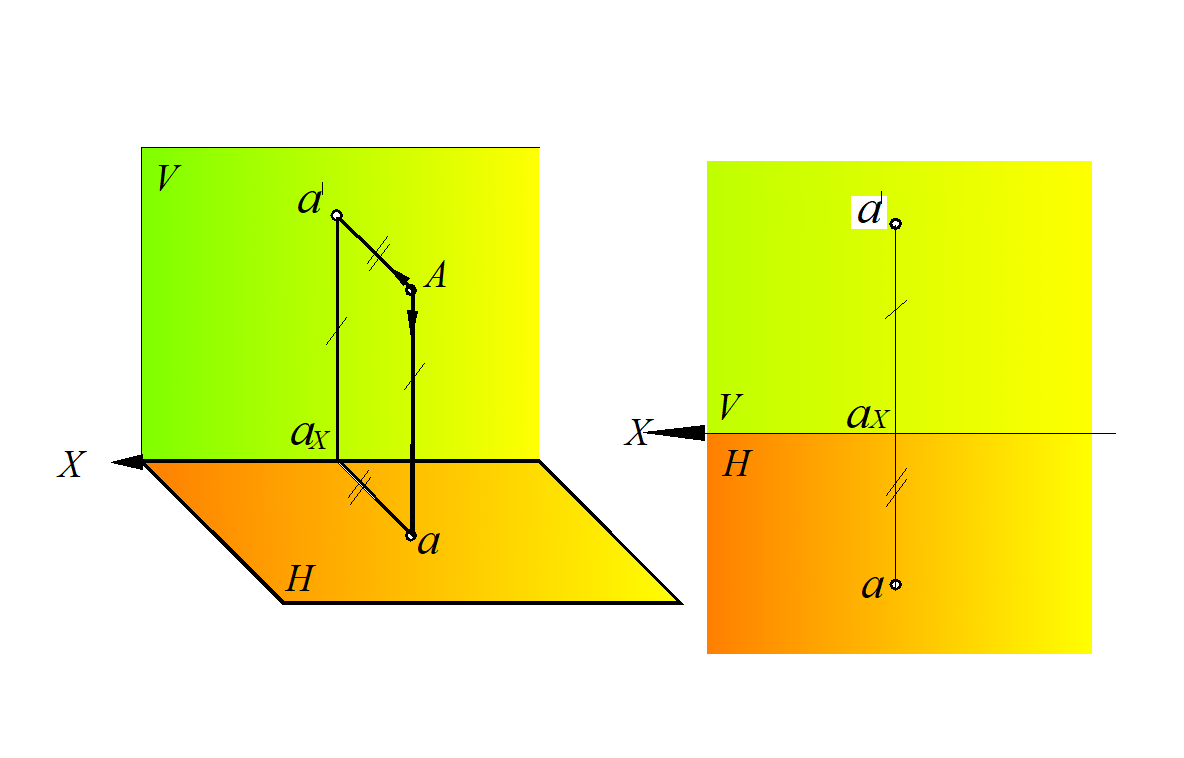
Рис. 5. Точка в системе двух плоскостей проекций:

а – модель; б,– эпюр

Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость Н совмещают вращением вокруг оси x с плоскостью V (рис. 1.5, б). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещены определенным образом одна с другой, называется эпюром (франц. Epure – чертеж.). Эпюр часто называют эпюром Монжа. Для упрощения эпюра границы плоскостей проекций не указывают (рис. 1.5, в).

На эпюре Монжа проекции а и а' окажутся расположенными на одном перпендикуляре к оси х. Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.

Трех плоскостей проекций

В практике изображения различных геометрических объектов, чтобы сделать проекционный чертеж более ясным, возникает необходимость использовать третью – профильную – плоскость проекций W, расположенную перпендикулярно к H и V (рис. 1.6). Эти плоскости образуют трехгранный угол. В соответствии с ГОСТ 2.305–68 плоскости проекций H , V , W относятся к основным плоскостям проекций. Линии пересечения плоскостей H , V , W  называются проекционными осями х, y , z .

Система трех взаимно перпендикулярных плоскостей аналогична декартовой системе координат. Примем H , V , W за координатные плоскости, точку о – за начало координат, проекционные оси x , y , z за координатные: ох – ось абсцисс; о y – ось ординат; о z – ось аппликат.

Координатные плоскости делят пространство на 8 частей – октантов, представляющих прямоугольные трехгранники.

 

 

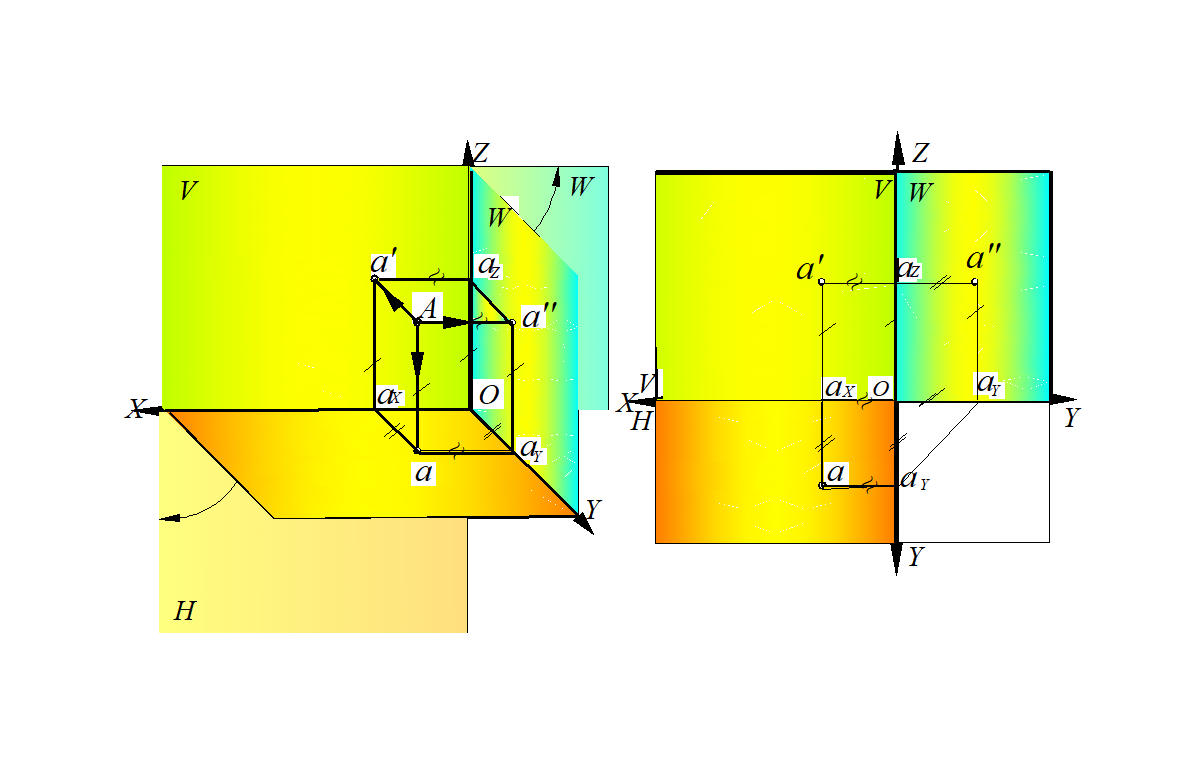
Рис. 6. Образование проекционного чертежа точки:

а – модель; б – эпюр

 

 

Теперь для каждой точки можно определить координаты относительно данной системы.

Построение проекций точек сопровождаем проведением отрезков, определяющих координаты точки.

x _А = [ оа_х ] – широта точки;

y _А = [ oa_y ] – глубина точки;

z_A = [oa_z ] – высота точки.

Для получения комплексного чертежа точки плоскости проекций Н и W совмещают с плоскостью V поворотом их на 90^○ (рис. 1.7).

 

2.ТОЧКА. Прямая

 

Положение прямой линии относительно плоскостей проекций: прямые частного и общего положения. Свойства чертежа прямых линий. Взаимное положение точки и прямой. Основные задачи на прямую: деление отрезка в заданном соотношении; определение натуральной величины отрезка прямой и углов наклона к плоскости проекции методом прямоугольного треугольника. Взаимное положение прямых. Проекции плоских углов.

Задача.

Задача.

Построить проекции точки А(–10; 40; –30) (рис. 8).

 

 

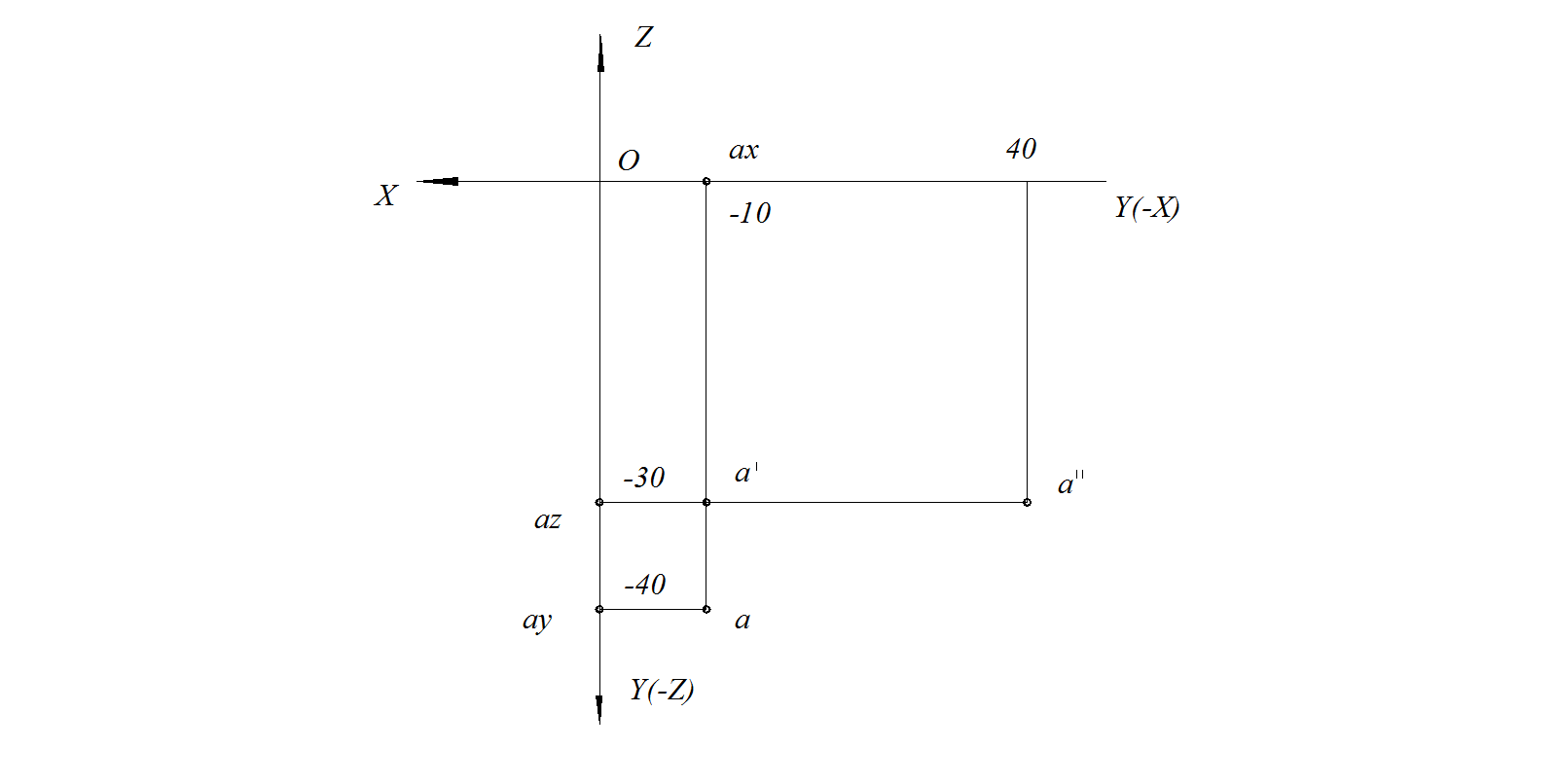
Рис. 8. Построение проекций точки А по координатам

 

 

Для построения фронтальной проекции а′ точки А справа от точки О на оси Х откладываем значение Х = –10. Вниз от точки О по направлению оси Z откладываем значение       Z = –30. Пересечением перпендикуляров из точек а _X и а _Z, восстановленных к соответствующим осям Х и Z, определяем точку а′.

Для построения горизонтальной проекции а точки А по направлению оси Y вниз от точки О откладываем значение y = – 40. Через точку а _Y проводим перпендикуляр до пересечения с линией связи а′а _X. Отмечаем точку а – горизонтальную проекцию точки А. По расположению фронтальной и горизонтальной проекций точки А определяем, что точка А расположена в VΙΙΙ октанте.

Для построения профильной проекции а′′ точки А через ее фронтальную проекцию а′ проводим линию связи а′а _Z и на ней, вправо от точки а _Z, откладываем значение y = 40. Отмечаем точку а′′ – профильную проекцию точки А.

 

Вывод. Положение точки в пространстве вполне определено, если известны три ее координаты или две любые ортогональные проекции. Как следствие из этого – по двум любым заданным ортогональным проекциям точки можно всегда построить недостающую ее третью ортогональную проекцию.

Рассмотри построение точки по двум заданным ортогональным проекциям.

Задача.

По двум заданным ортогональным проекциям построить недостающую проекцию точки В (рис. 9).

 

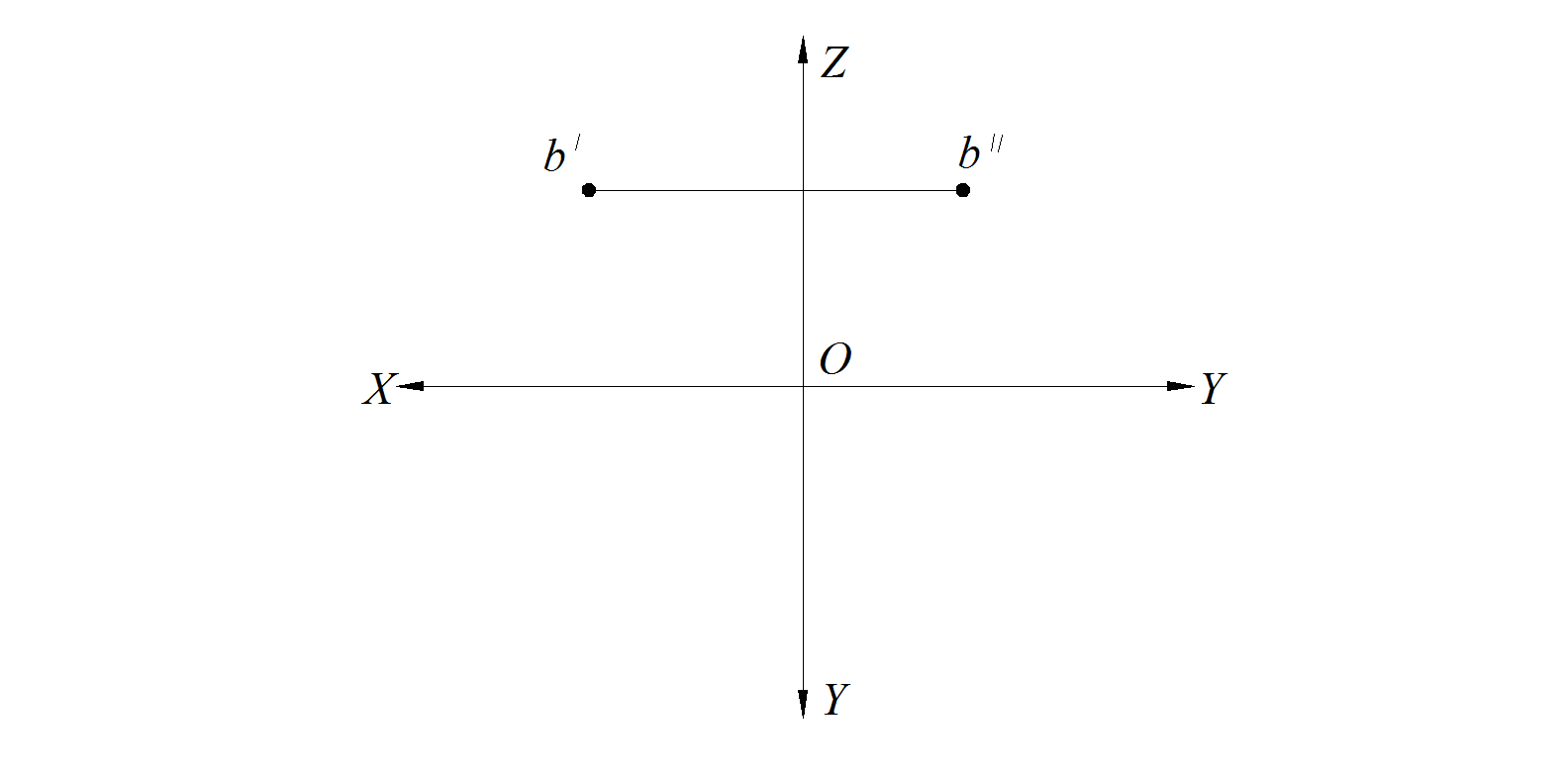
Рис. 9. Графическое условие задачи

 

Решение:

 Анализируем графическое условие задачи: заданы фронтальная и профильная проекции точки В. Это значит, заданы все три координаты точки В. Следовательно, необходимо построить ее горизонтальную проекцию.

Порядок выполнения графической части задачи:

1. Для построения горизонтальной проекции точки В необходимо знать Х_В и У_В. Эти координаты находим на чертеже.

2. Замеряем У_В = b_Z b ′′ и откладываем эту координату вдоль линии связи от оси ОХ от точки b _Х .

3. Строим горизонтальную проекцию точки В (рис. 10).

 

 

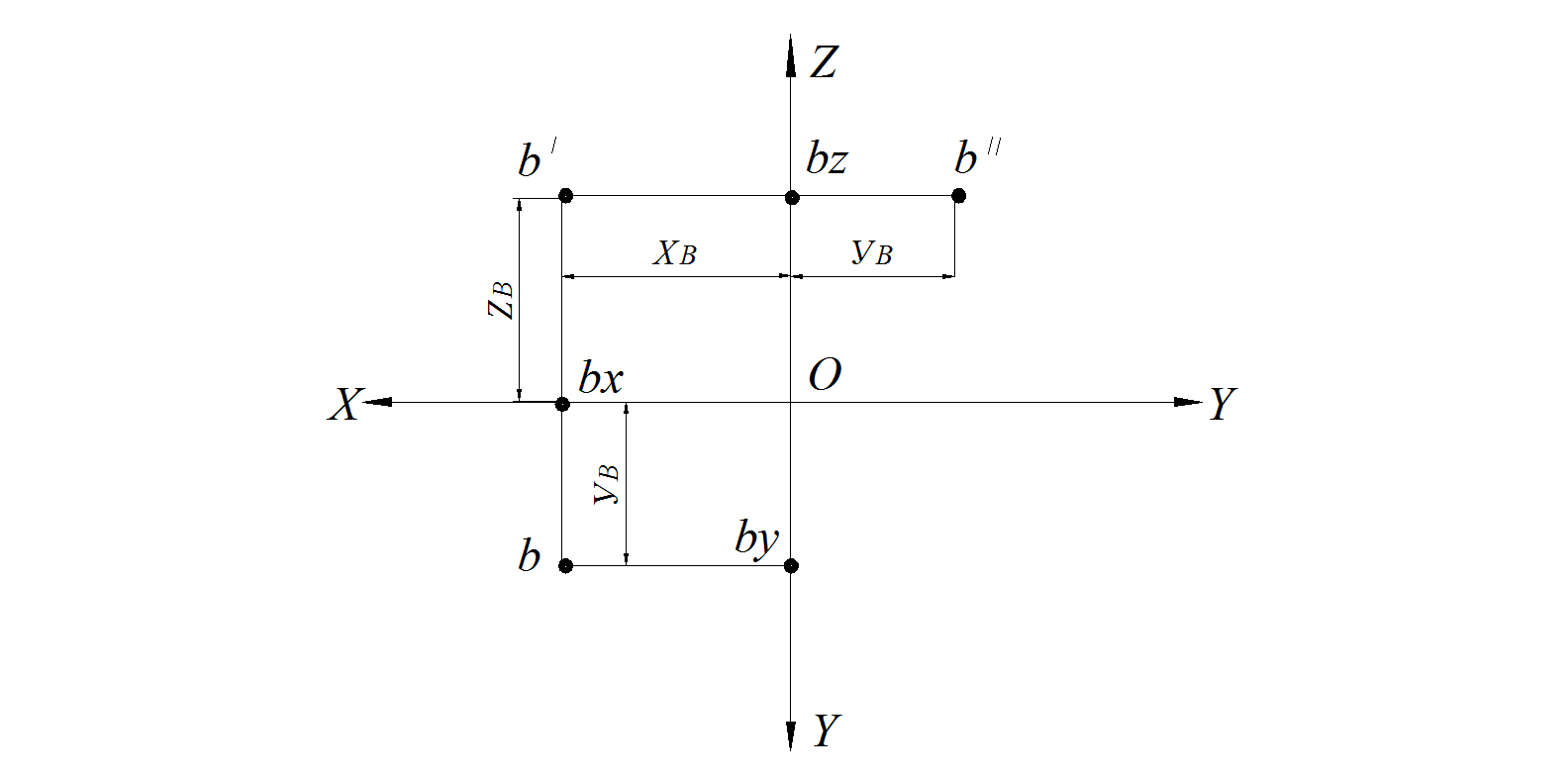
Рис. 10. Построение недостающей проекции

 

 

Прямая линия

Прямая линия – одно их основных понятий геометрии. Ее можно рассматривать как непрерывное однопараметрическое положение множества точек, следовательно, можно утверждать, что прямая линия бесконечна.

Прямая линия в линейной алгебре – линия первого порядка. Ее уравнение:

 

Ах + By + C = 0,

 

где А, В, С – любые постоянные.

Самый простой способ определения прямой в пространстве – найти две точки этой прямой. Соединив их, получим отрезок, вполне определяющий данную прямую. Для построения проекций прямой, строим проекции двух точек. Соединяем одноименные проекции точек. Получаем проекции отрезка данной прямой.

 

При ортогональном проецировании на плоскости проекций прямая линия проецируется в виде прямой. Чтобы построить проекции этой прямой линии, проходящей через заданные точки А и В, нужно построить проекции этих точек и провести прямые линии через их одноименные проекции (рис. 11). Получим:

аb – горизонтальную проекцию отрезка прямой;

а′b′ – фронтальную проекцию отрезка прямой.

 

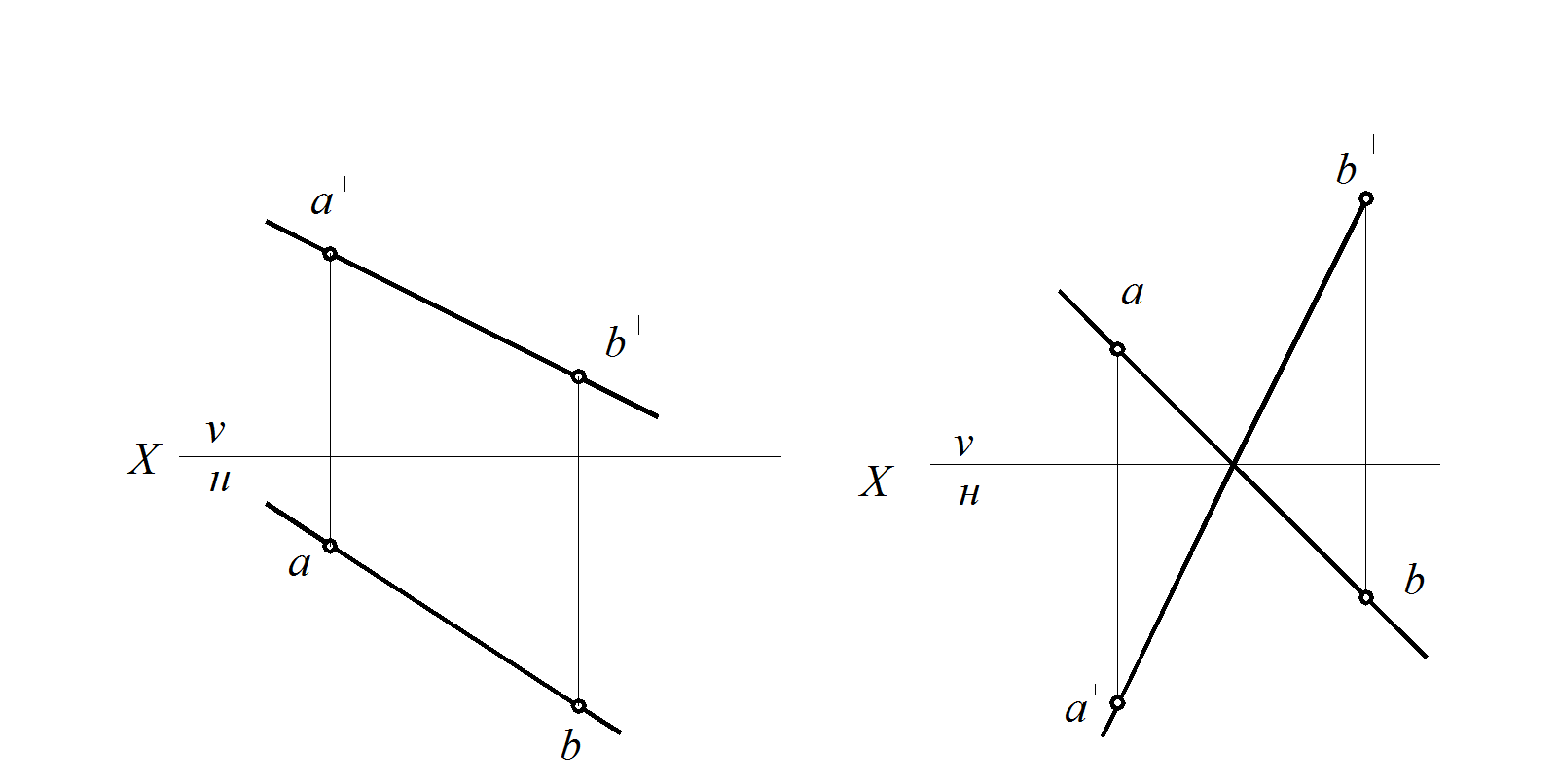
Рис. 11. Проекции отрезка прямой, проходящего через две точки

 

 

Следы прямой

Прямая пересекает плоскости проекций в точках, которые называются следами прямой.

Точка пересечения прямой N с горизонтальной плоскостью проекций Н (П₁) называется горизонтальным следом N _H .

Точка пересечения прямой с фронтальной плоскостью проекций V (П₂) – фронтальным следом N _V.

Точка пересечения прямой N с профильной плоскостью проекций W (П₃) – профильным следом N _W прямой.

Вывод:

· горизонтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в горизонтальной плоскости проекций H (П₁);

· фронтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая во фронтальной плоскости проекций V (П₂);

· профильный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в профильной плоскости проекций W (П₃).

 

 Задача.

Построить точки пересечения прямой N с горизонтальной Н (П₁) и фронтальной V(П₂) плоскостями проекций (рис. 12 а,б).

 

Анализируя задачу, приходим к выводу, что необходимо построить горизонтальный и фронтальный следы прямой.

Решение:

 

 1. Построение фронтального следа N _V .

 Необходимо построить точку, принадлежащую прямой N и фронтальной плоскости проекций. Согласно изложенному ранее материалу, горизонтальная проекция искомой точки должна:

– лежать на оси Х;

– принадлежать горизонтальной проекции прямой N.

Порядок выполнения графической части задачи:

1.1. Отмечаем точку пересечения горизонтальной проекции n прямой N с осью Х, получаем точку n _V – горизонтальную проекцию фронтального следа.

1.2. Через точку n _V проводим линию связи перпендикулярно оси Х.

1.3. Находим точку пересечения линии связи с фронтальной проекцией n′ прямой N, получаем точку N _V – фронтальную проекцию фронтального следа. Через эту точку прямая уходит во вторую четверть (рис. 12,а) и в третью четверть (рис. 12, б).

2. Построение горизонтального следа N _H .

 Необходимо построить точку, принадлежащую прямой N и горизонтальной плоскости проекций Н. Согласно изложенному ранее материалу, фронтальная проекция искомой точки должна:

– лежать на оси Х;

– принадлежать фронтальной проекции прямой N.

Порядок выполнения графической части задачи:

2.1. Отмечаем точку пересечения фронтальной проекции n′ прямой N с осью Х, получаем точку n _H – фронтальную проекцию горизонтального следа.

2.2. Через точку n _H проводим линию связи перпендикулярно оси Х.

2.3. Находим точку пересечения линии связи с горизонтальной проекцией n прямой N, получаем фронтальную проекцию фронтального следа. В этой точке прямая пересекает горизонтальную плоскость и уходит в четвертую четверть (рис. 12 а,б).

 

а

б

 

 

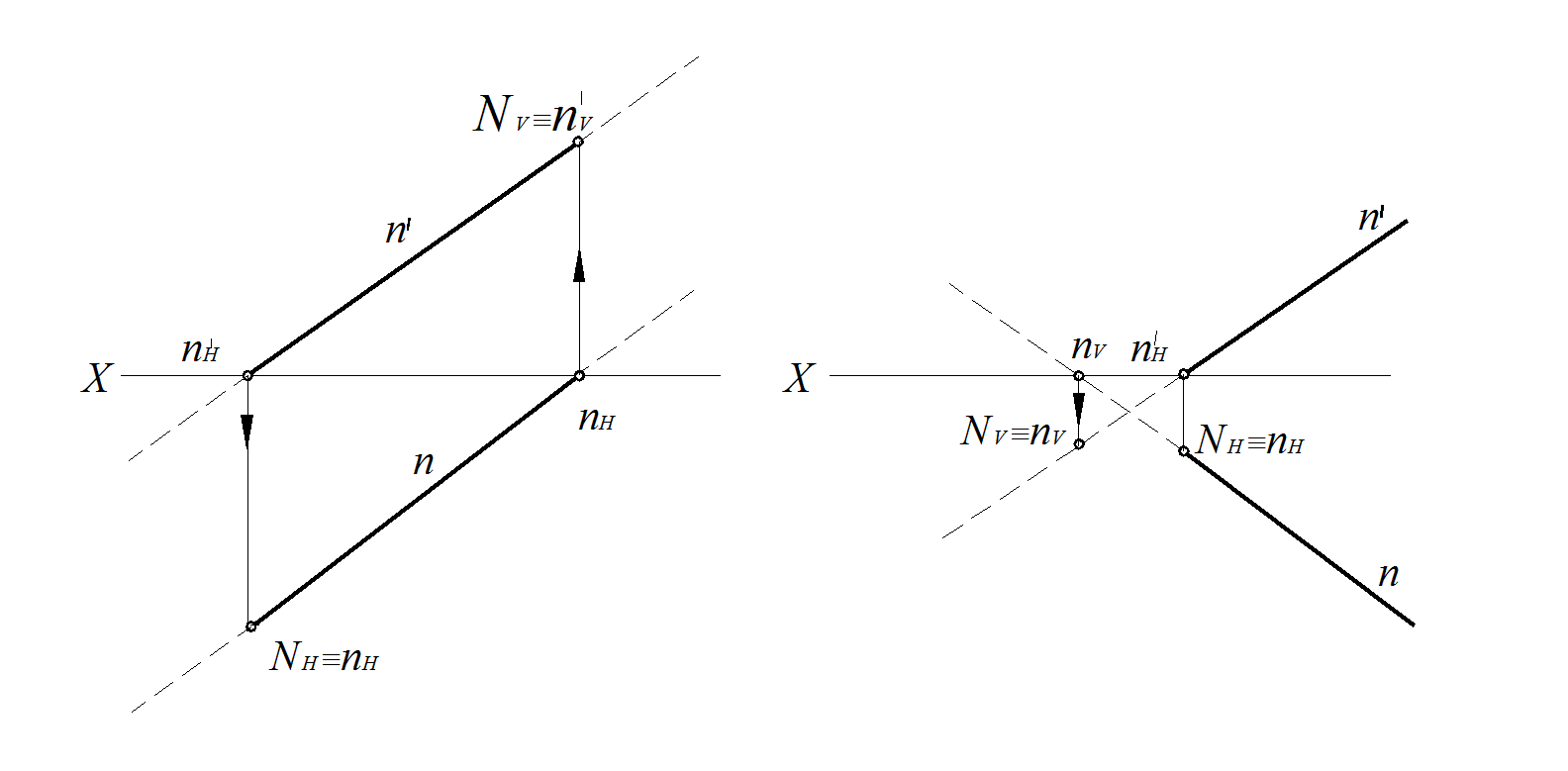
Рис. 12. Построение следов прямой линии N:

а – прямая уходит во вторую четверть; б – прямая уходит в третью четверть

 

Задача.

Построить горизонтальный и фронтальный следы прямой(рис. 13).

Решение:

1. Горизонтальный след прямой - это точка, лежащая одновременно на прямой АВ и в горизонтальной плоскости проекций. Следовательно, ее фронтальная проекция будет лежать на оси Х и на фронтальной проекции АВ. Продолжаем фронтальную проекцию прямой АВ до пересечения с осью Х. Полученная точка Сн будет горизонтальным следом прямой АВ.

2. Фронтальный след прямой - это точка, лежащая одновременно на прямой АВ и во фронтальной плоскости проекций. Следовательно, ее горизонтальная проекция будет лежать на оси Х и на горизонтальной проекции АВ. Продолжаем горизонтальную проекцию прямой АВ до пересечения с осью Х. Полученная точка С V будет фронтальным следом прямой АВ.

 

 

 

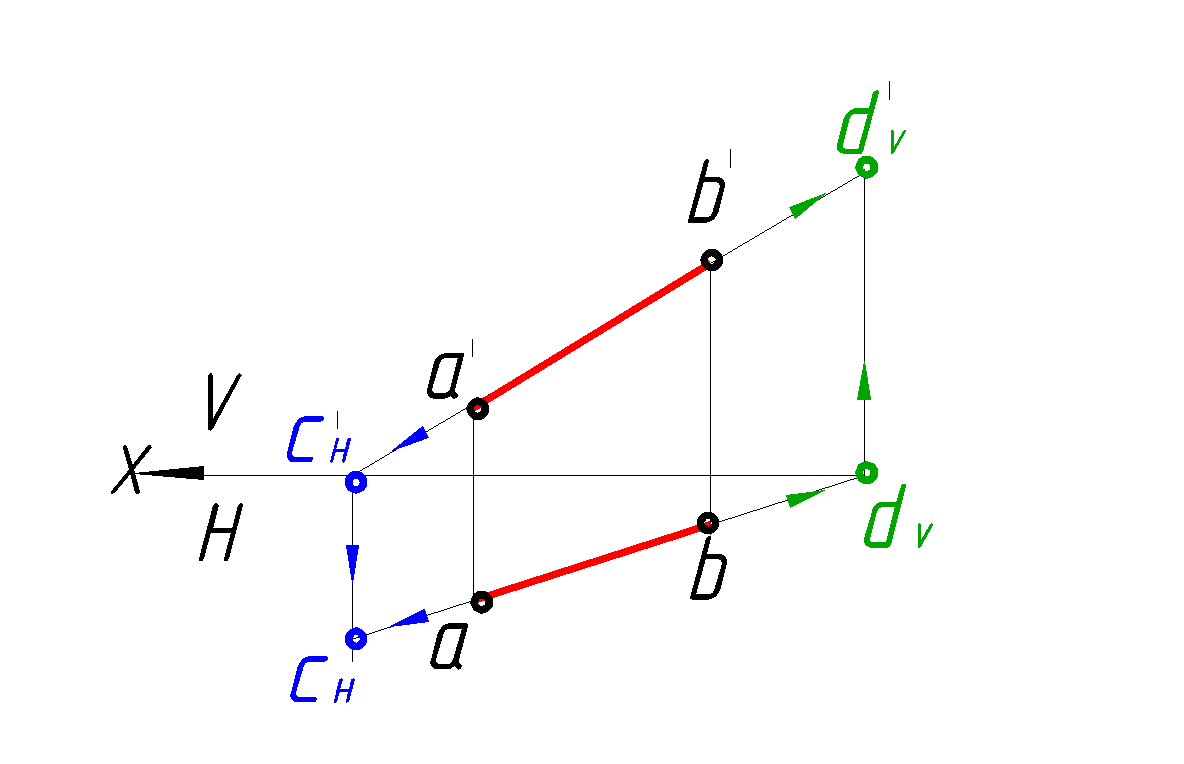
Рис. 13. Построение следов прямой линии АВ

 

 

Прямые уровня

Прямая уровня может лежать в самой плоскости проекций. Такую прямую называют линией нулевого уровня.

Горизонтальная прямая уровня или горизонталь – прямая линия, параллельная горизонтальной плоскости проекций.

 Рассмотрим рис. 15, а: отрезок прямой АВ параллелен плоскости проекций Н; следовательно, каждая точка данного отрезка прямой имеет постоянную координату Z, т. е. имеет одинаковую высоту. Поэтому фронтальная проекция отрезка a ′ b ′ параллельна оси Х и является характерной проекцией.

Длина горизонтальной проекции отрезка равна его натуральной величине ([ab] = [AB]); угол β, образованный горизонтальной проекцией и осью Х, равен углу наклона прямой к фронтальной плоскости проекций (рис. 14, б).

б

                                                              

а

 

 

 

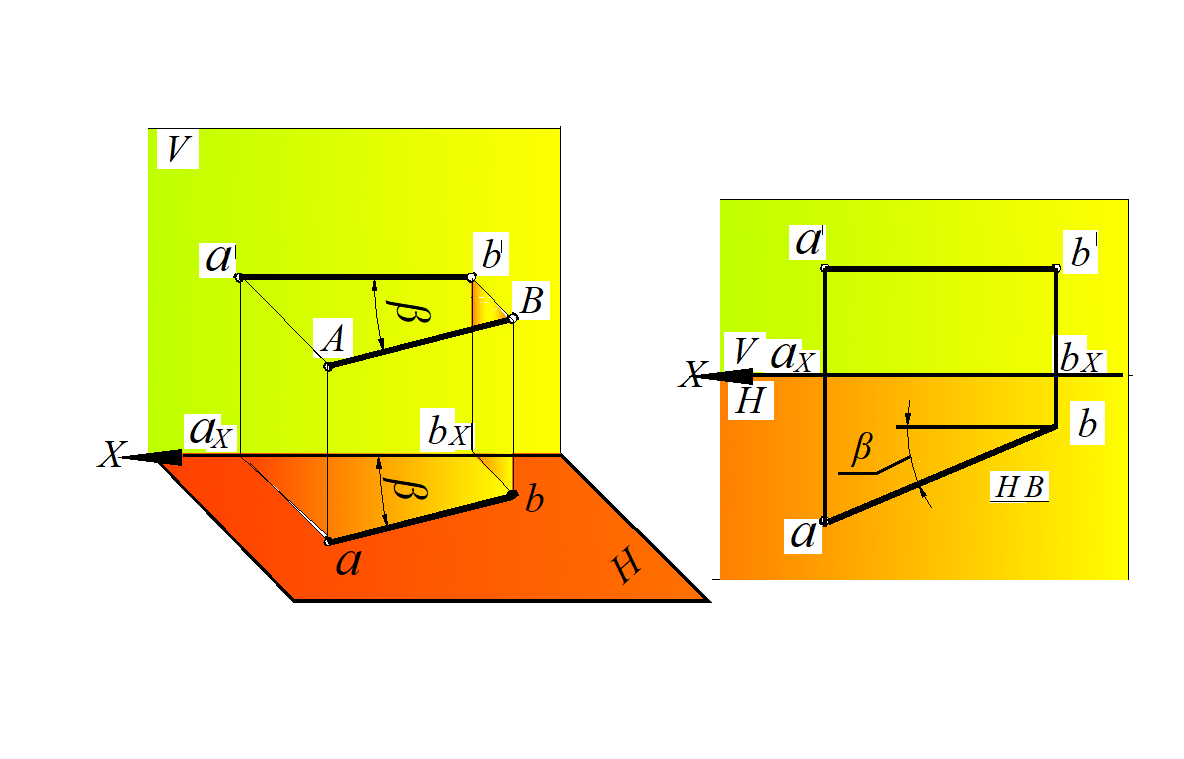
Рис. 15. Горизонтальная прямая уровня:

а – в пространственной модели; б – на эпюре Монжа

 

Фронтальная прямая уровня или фронталь – прямая линия, параллельная фронтальной плоскости проекций.

 Рассмотрим рис. 16, а: отрезок прямой CD параллелен фронтальной плоскости проекций V, следовательно, координата Y для каждой точки данного отрезка прямой постоянная, т. е. точки имеют одну и ту же глубину, поэтому горизонтальная проекция cd параллельна оси Х. Эта проекция является характерной для фронтали. Длина фронтальной проекции отрезка равна его натуральной величине ([c׳d׳] = [CD]); угол α, образованный фронтальной проекцией и осью Х, равен углу наклона отрезка прямой к горизонтальной плоскости проекций (рис. 16, б).

б

а

 

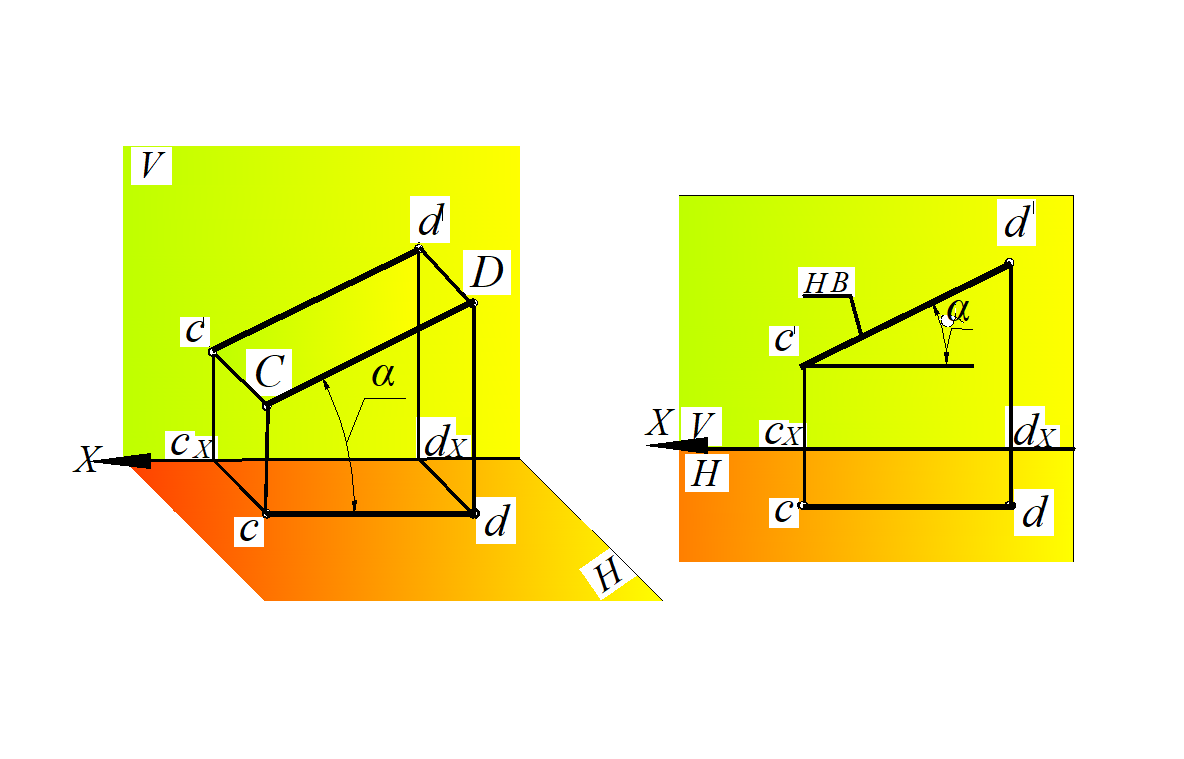
Рис. 16. Фронтальная прямая уровня:

а – в пространственной модели; б – на эпюре Монжа

 

Профильная прямая уровня – прямая линия, параллельная профильной плоскости проекций.

Рассмотрим рис. 17, а: отрезок прямой EF параллелен плоскости W, следовательно, каждая точка данного отрезка прямой имеет постоянную координату Х, т. е. точки имеют одну и ту же широту. Поэтому, (e׳f׳) || [OX) и (ef) || [OY); длина профильной проекции отрезка равна его натуральной величине ([e ′′ f′′] = [EF]); углы α и β, образованные профильной проекцией с осями Z и Y, равны углам наклона прямой к горизонтальной и фронтальной плоскостям проекций соответственно (рис. 17, б).

 

                              а                                                   б

 

 

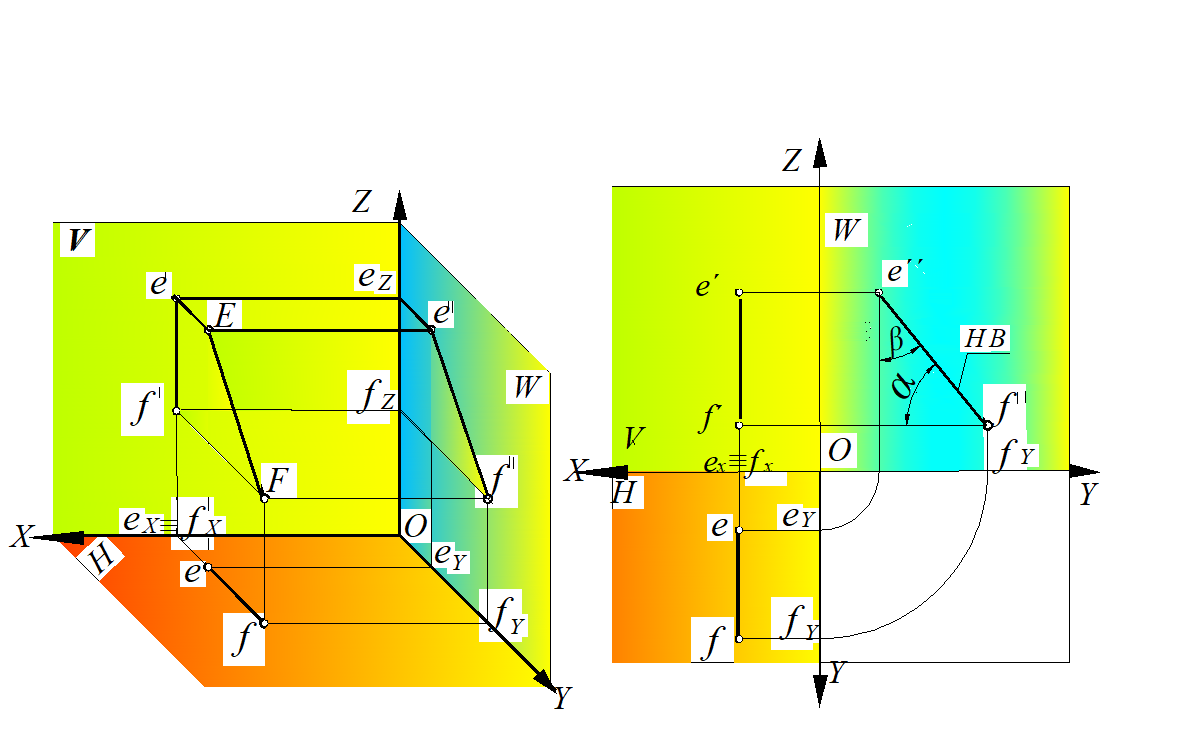
         Рис.17. Профильная прямая уровня:

а – в пространственной модели; б – на эпюре Монжа

 

Свойства чертежей прямых уровня:

1) отрезки таких прямых проецируются в натуральную величину на ту плоскость проекций, которой они параллельны;

2) на непараллельные ей плоскости проекций прямая линия проецируется в прямую, параллельную соответствующим проекционным осям;

3) угол, образованный проекцией прямой уровня на параллельной ей плоскости и проекционной осью, определяет натуральную величину угла этой прямой к непараллельной ей плоскости.

                  

 

Проецирующие прямые

Прямые линии, перпендикулярные одной из плоскостей проекций, называются проецирующими прямыми.

Горизонтально проецирующая прямая – прямая линия, перпендикулярная горизонтальной плоскости проекций.

Рассмотрим рис. 18: отрезок прямой АВ перпендикулярен горизонтальной плоскости проекций Н, следовательно, параллелен фронтальной V и профильной W плоскостям проекций; фронтальная проекция a ′ b′ отрезка прямой перпендикулярна оси Х, а также она равна натуральной величине отрезка АВ; горизонтальная проекция отрезка прямой вырождается в точку, т. к. горизонтальные проекции точек А и В совпадают. Такие точки, лежащие на одном проецирующем луче, называются конкурирующими относительной плоскости проекций, к которым перпендикулярна данная прямая.

Видимость точек определяют на той плоскости проекций, где проекции точек совпадают. Будет видна та точка, координата которой больше. На рис. 18,б будет видимой точка А, т. к. координата Z точки А больше, чем координата Z точки В, т. е. точка А находится выше точки В. Все остальные координаты этих точек одинаковые. Невидимую точку на чертеже заключают в скобки.

 

                     а                                                      б

 

 

 

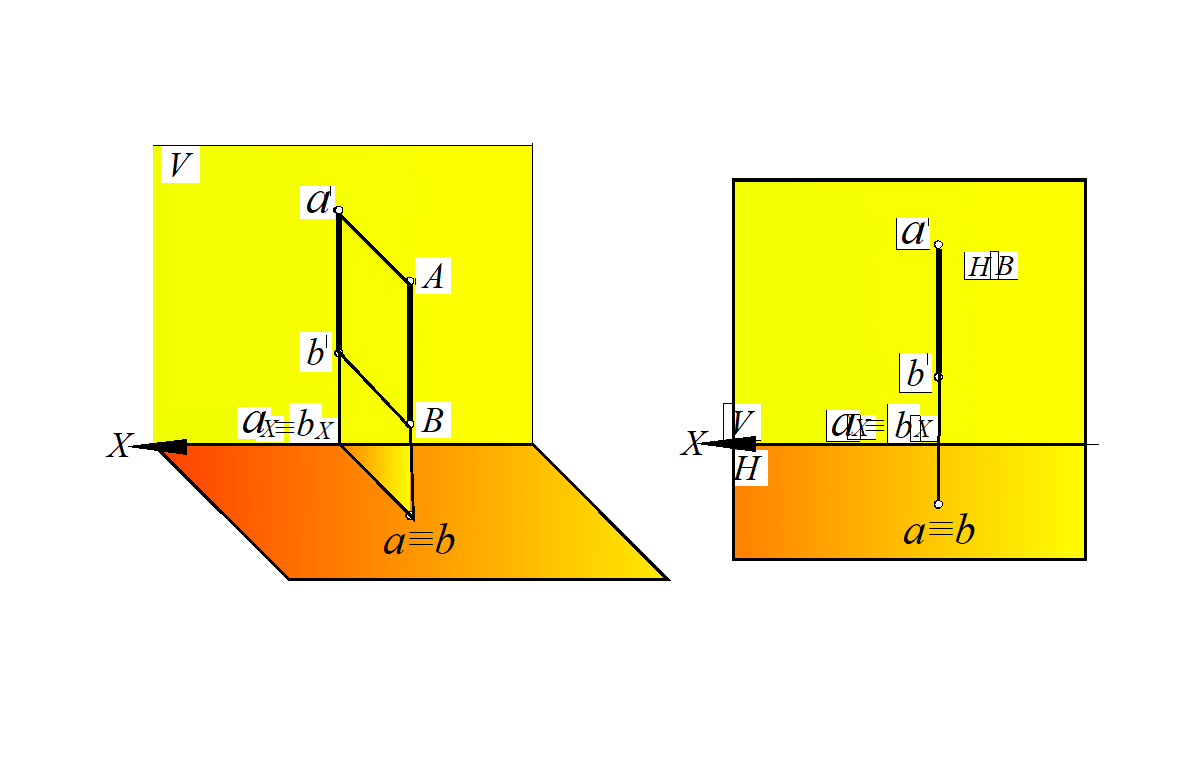
Рис. 18. Горизонтально проецирующая прямая:

а – в пространственной модели; б – на эпюре Монжа

Фронтально проецирующая прямая – прямая линия, перпендикулярная фронтальной плоскости проекций.

Рассмотрим рис. 19: отрезок прямой CD перпендикулярен фронтальной плоскости проекций V, следовательно, параллелен горизонтальной Н и профильной W плоскостям проекций; горизонтальная проекция отрезка прямой перпендикулярна оси Х, а также она равна натуральной величине отрезка CD; на фронтальной плоскости проекций отрезок отображается в точку, т. е. фронтальные проекции точек С и D совпадают. Видимой будет точка D, т. к. Y_D >Y_C , т. е. точка D будет находиться перед точкой С (рис. 19, б).

 

а

б

 

 

   

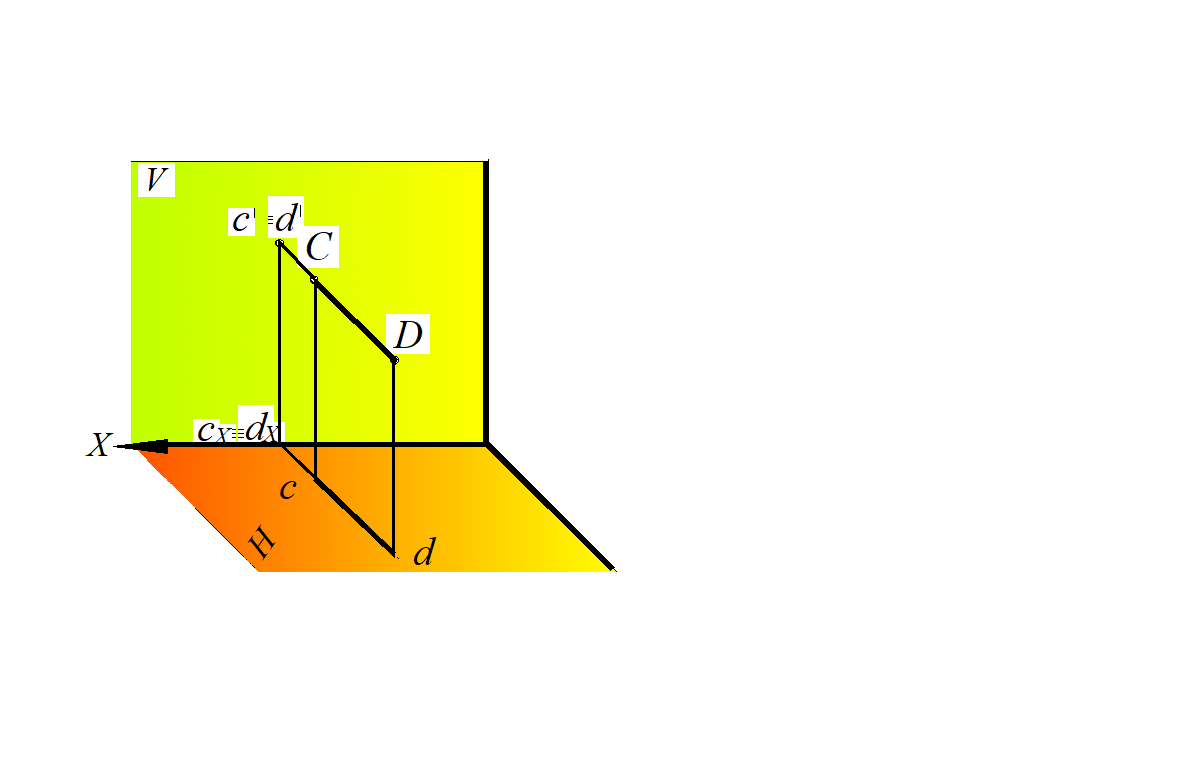
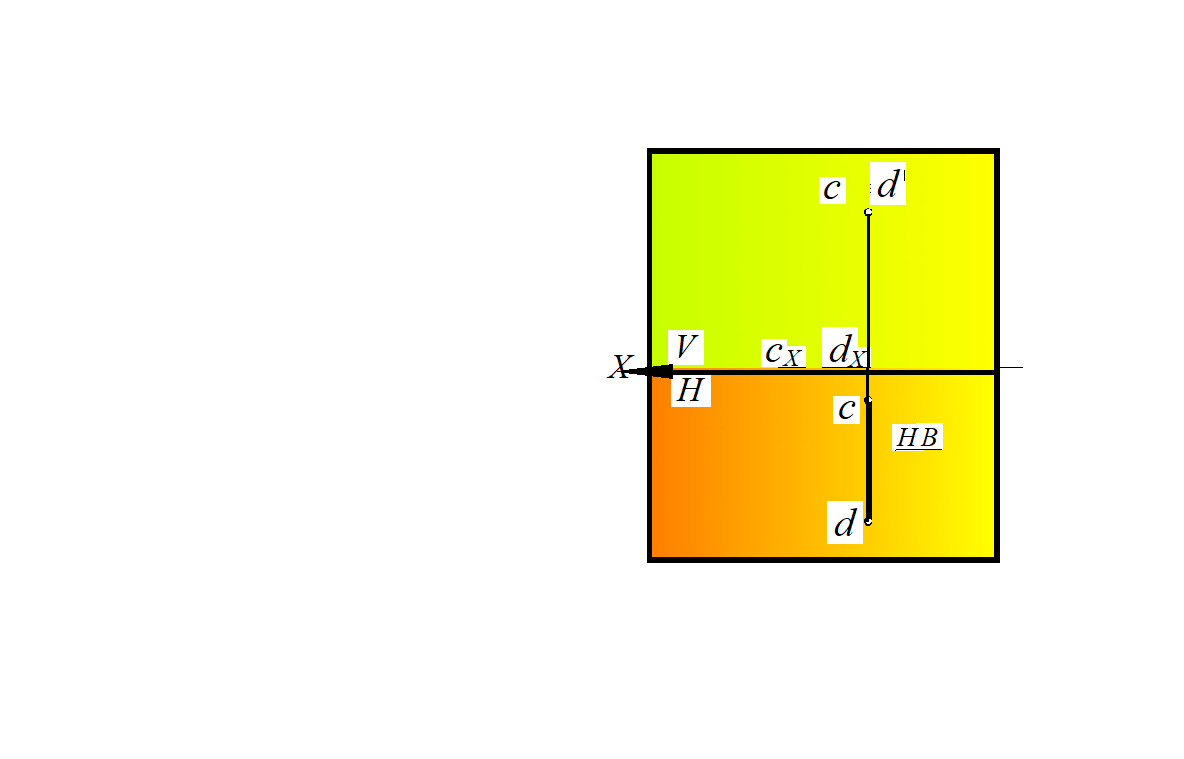
Рис. 19. Фронтально проецирующая прямая:

а – в пространственной модели; б – на эпюре Монжа

 

 

Профильно проецирующая прямая – прямая линия, перпендикулярная профильной плоскости проекций.

Рассмотрим рис. 20, а. Отрезок прямой EF перпендикулярен профильной плоскости проекций W, следовательно, параллелен горизонтальной Н и фронтальной V плоскостям проекций. Горизонтальная и фронтальная проекции этого отрезка прямой параллельны оси Х, а на профильной плоскости проекций отрезок прямой отобразится в точку. Видимой на профильной плоскости проекций будет точка Е, т. к. Х_Е > Х _F . Горизонтальная проекция ef и фронтальная проекция e׳f׳ отрезка прямой будут равны натуральной величине отрезка |ef| = |e׳f׳| = = |EF| (рис. 20, б).

 

                           а                                               б

 

 

 

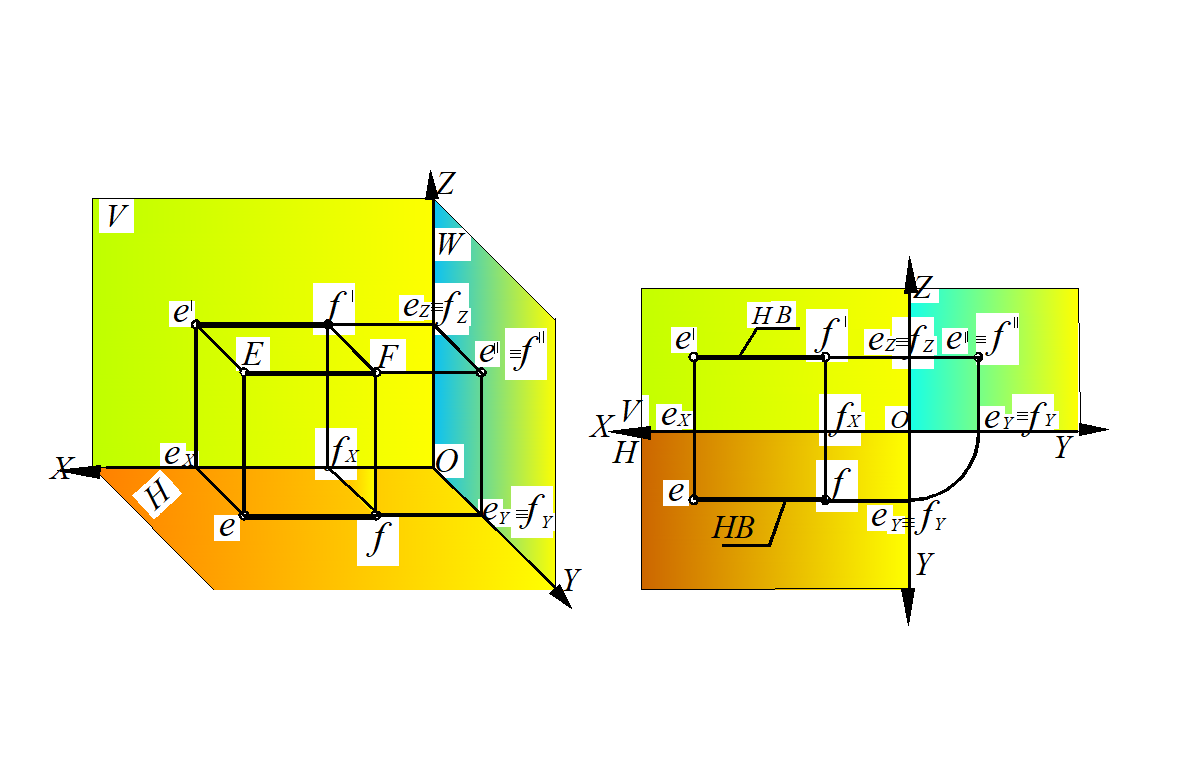
 Рис. 20. Профильно проецирующая прямая:

а – в пространственной модели; б – на эпюре Монжа

 

Вывод: проецирующая прямая определяется на чертеже одной своей проекцией (в виде точки) на той плоскости проекций, к которой эта прямая перпендикулярна. На остальные плоскости проекций эта прямая проецируется без искажения, т. е. в натуральную величину

 

 

Свойства чертежей проецирующих прямых:

1) прямая, перпендикулярная плоскости проекций, проецируется на нее в точку, т. к. все точки ее являются конкурирующими – лежат на одном проецирующем луче;

2) на две другие плоскости проекций прямая проецируется в прямые, перпендикулярные соответствующим проекционным осям;

3) проекции отрезков равны действительной величине отрезков таких прямых.

Если такие прямые задают отрезками, то из всех конкурирующих точек отрезка на соответствующей плоскости проекций будет видимой та, у которой соответствующая координата максимальна. Невидимые точки показывают в скобках.

Прямые частного положения не имеют следа на той плоскости, которой они параллельны.

 

Основные задачи на прямую

Задача.

 На отрезке прямой АВ построить точку С, которая делит данный отрезок в отношении 2:3 от точки A (рис. 27).

Решение.

 Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекция этой точки делит одноименные проекции отрезка в том же отношении. Следовательно, чтобы разделить отрезок прямой в заданном отношении, достаточно разделить в этом же отношении одну из проекций данного отрезка.

Порядок выполнения графической части задачи:

1. Выбираем любую из проекций отрезка АВ, например, фронтальную – a ′ b ′.

2. Из точки b ′ проводим луч под любым углом к отрезку a ′ b ′. Так как отрезок АВ необходимо разделить в отношении 2:3, то равных частей на отрезке должно быть отложено 5 (2+3).

3. Задаемся произвольным единичным отрезком и откладываем от точки b ′ вдоль луча пять равных отрезков. Последнюю пятую точку обозначаем А_о и соединяем с точкой а′.

4. На отрезке |А_ob ′| отсчитываем от точки A_o два равных отрезка. Получаем точку С_о, которая делит отрезок А_оb ′ в отношении 2:3.

5. Параллельно отрезку |a ′А_о| через точку С_о проводим прямую. Получаем на отрезке a ′ b ′ точку с′, которая делит отрезок a ′ b ′ в отношении 2:3.

6. Горизонтальную проекцию точки С (с) находим по свойству принадлежности: проводим из точки с′ линию связи до пересечения с горизонтальной проекцией отрезка прямой АВ (а b ).

7. Построенная проекция точки С делит заданный отрезок прямой АВ в отношении 2:3.

 

 

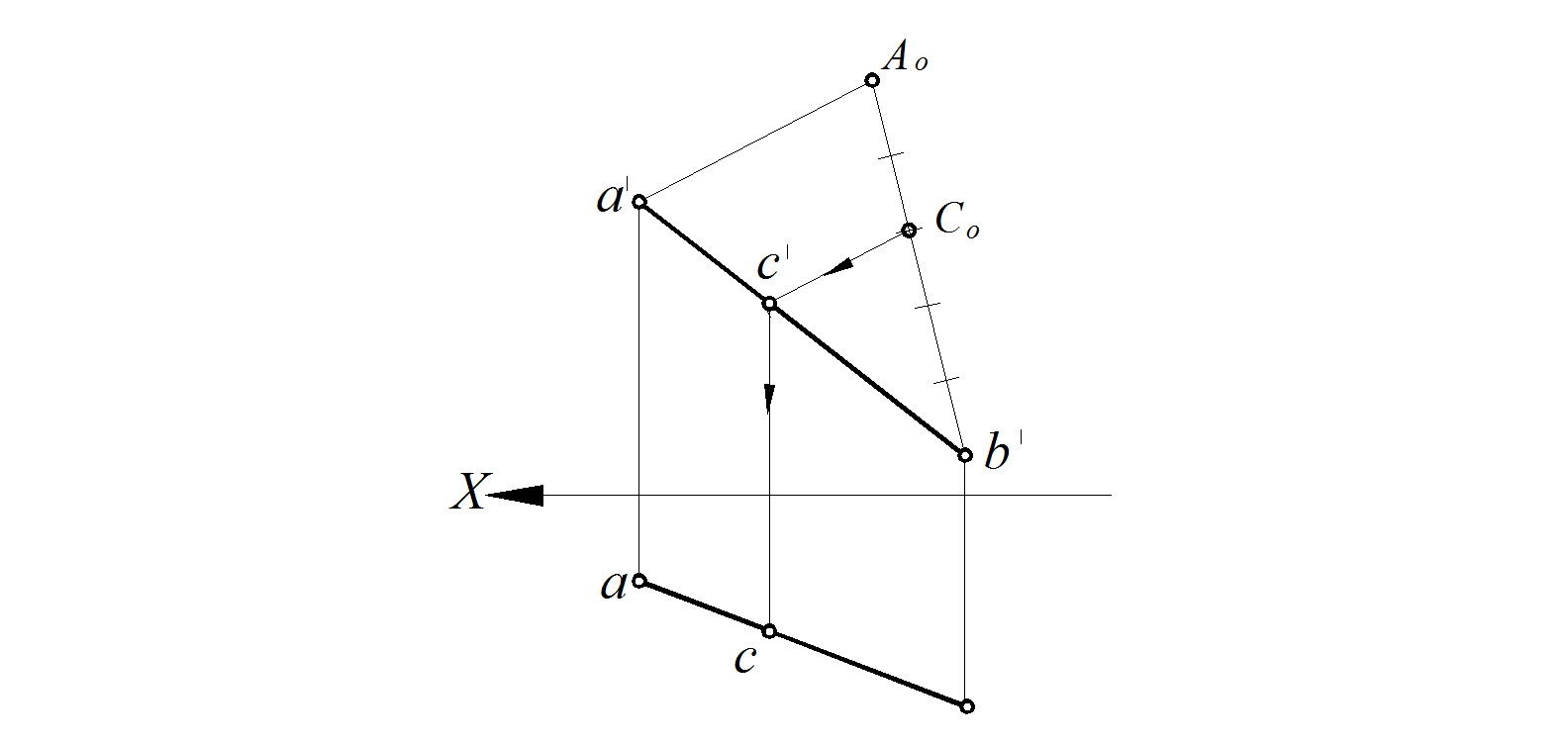
Рис. 27. Деление отрезка в заданном отношении

2. Определение натуральной величины отрезка прямой общего положения и определение углов наклона ее к плоскостям проекций

На плоскости проекций отрезок прямой общего положения проецируется с искажением. Для решения метрических задач необходимо определить натуральную величину отрезка прямой или угол наклона его к основным плоскостям проекций. Существует несколько методов определения натуральной величины отрезка прямой.

 

Задача 1.

Определить длину отрезка прямой АВ и угол наклона его к горизонтальной плоскости проекций Н ( ∠ α_АВ) (рис. 28).

Решение:

Необходимо проанализировать графическое и словесное условие задачи:

1. Графический анализ проводится относительно осей проекций: отрезок прямой АВ занимает общее положение, т. к. ни одна проекция отрезка прямой не является характерной (параллельной или перпендикулярной оси Х). Следовательно, ни одна проекция отрезка не дает нам натуральной величины данного отрезка непосредственно на чертеже.

2. Словесное условие говорит о том, что дополнительные построения необходимо выполнять на горизонтальной проекции отрезка, т. к. требуется найти угол наклона отрезка к горизонтальной плоскости проекций – ∠α_АВ. В этом случае прямоугольный треугольник нужно строить, принимая за один его катет горизонтальную проекцию аb.

Далее, графические построения выполняются по приведенному ниже плану.

Порядок выполнения графической части задачи:

1. Проводим луч [а) ⊥ [аb] (либо из точки b).

2. Находим величину второго катета – |аА_о| = Z_А – Z_В = ∆Z (разность удаления концов отрезка до горизонтальной плоскости проекций).

3. Гипотенуза А_оb равна натуральной величине отрезка АВ |AB| = |A_ob| = 40 мм.

4. Угол между гипотенузой |A_ob| и проекцией |ab| является углом наклона отрезка АВ к плоскости проекций Н – α_АВ.

 

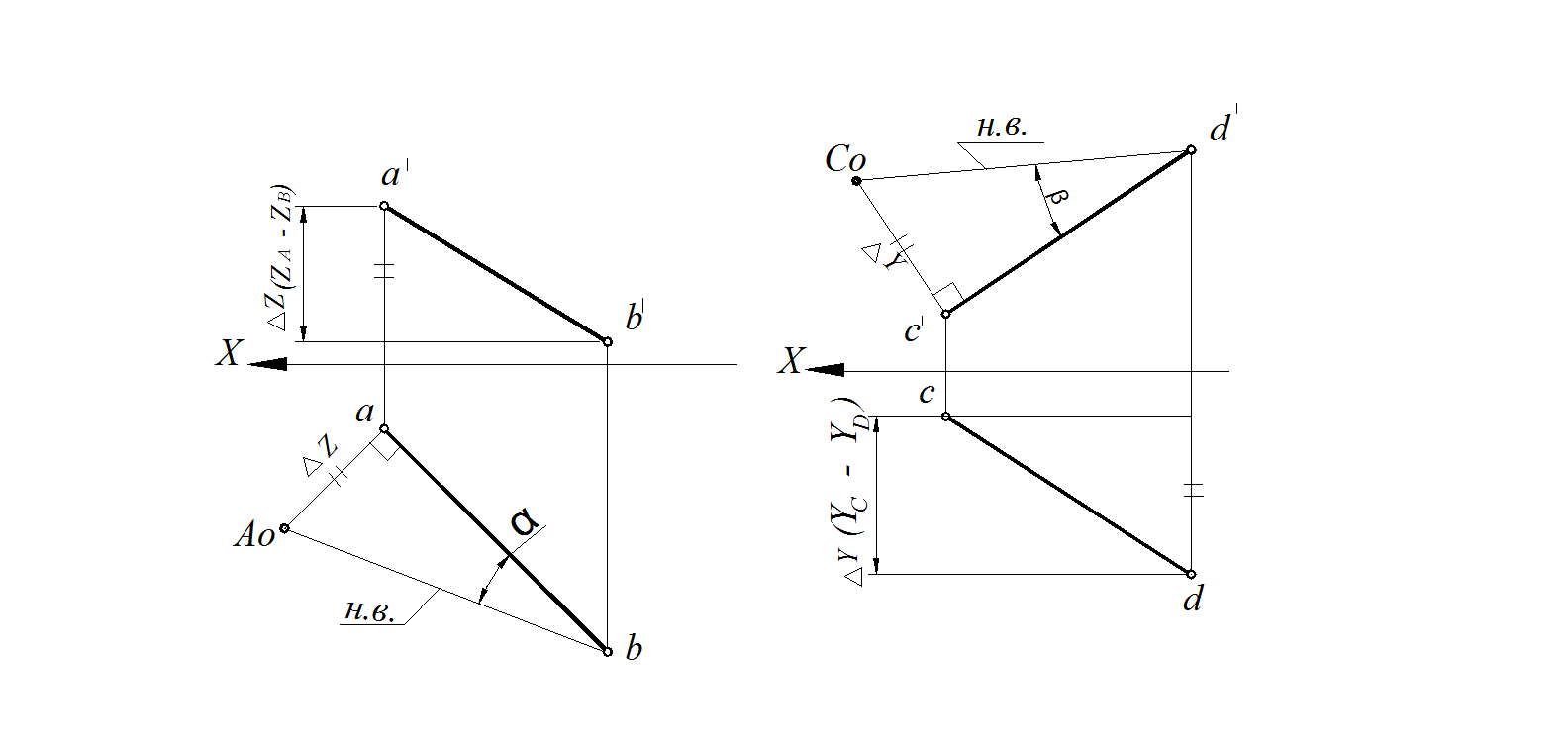
Рис. 28. Определение ∠α_АВ                                     Рис. 29. Определение ∠β_{С D}

 

Задача 2.

Определить угол наклона отрезка СD к плоскости проекций V (рис. 29).

Решение.

Анализ условия задачи аналогичен задаче, рассмотренной выше.

При определении угла наклона отрезка прямой к плоскости проекций V прямоугольный треугольник нужно строить, принимая за один его катет фронтальную проекцию данного отрезка, а величина второго катета представляет собой разность расстояний концов отрезка до фронтальной плоскости проекций, т. е. разница координат Y.

Порядок выполнения графической части задачи:

1. Проводим луч [c') ⊥ [c'd'] (либо из точки d').

2. Откладываем на луче [c') величину второго катета |c'C_o| = Y _С – Y_D = ∆Y .

3. Гипотенуза C_od' с отрезком c'd' образует ∠β, являющийся углом наклона [CD] к плоскости проекций V – ∠β_{С D}.

 

Взаимное положение прямых

Прямые в пространстве могут занимать различные положения относительно друг друга: быть параллельными, пересекаться и скрещиваться.

 

Пересекающиеся прямые

Если прямые пересекаются в пространстве в определенной точке, то их одноименные проекции пересекаются в проекциях этой же точки (рис. 30).

Если АВ ∩ CD = (∙) I => ab ∩ cd = 1; a ′ b′ ∩ c ′ d′ = 1′a ′′ b′′ ∩ c ′′ d′′ = 1′′.

Правильным будет и обратное утверждение: если на чертеже одноименные проекции прямых пересекаются, а проекции точки их пересечения лежат на одной линии связи, то прямые пересекаются в пространстве в этой же точке.

 

 

 

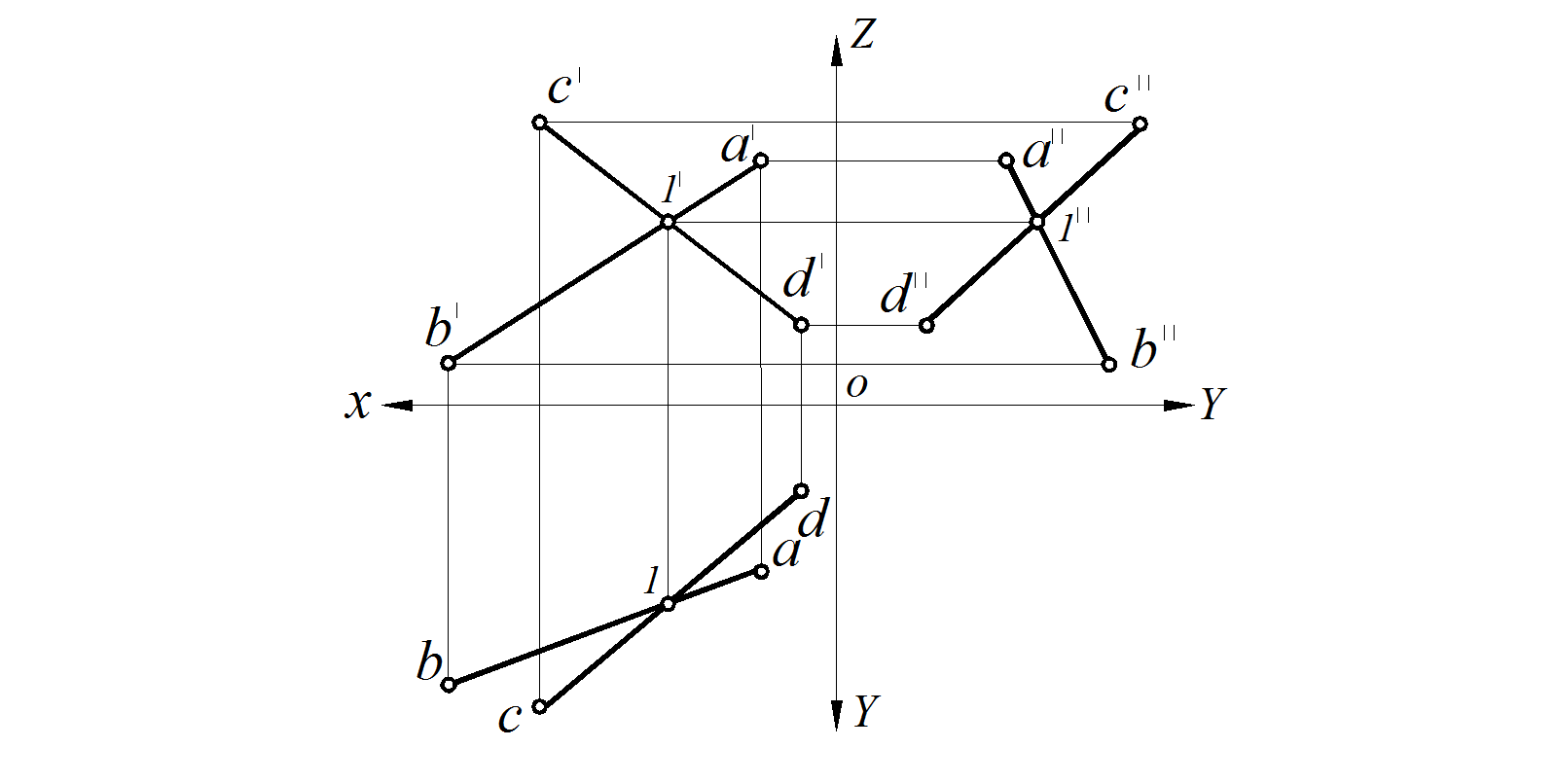
Рис. 30. Пересекающиеся прямые АВ и С D

 

Параллельные прямые

По свойству параллельного проецирования известно, что одноименные проекции параллельных прямых параллельны между собой. Рассмотрим данное свойство на примере параллельных отрезков прямых АВ и С D.

Дано АВ || С D, следовательно, на чертеже их одноименные проекции будут параллельны между собой (рис. 31): ab || cd, a ′ b′ || c ′ d ′ , a ′′ b ′′ || c ′′ d ′′, а также этому свойству соответствует обратное свойство: если на чертеже одноименные проекции прямых параллельны между собой, то в пространстве эти прямые параллельны.

 

 

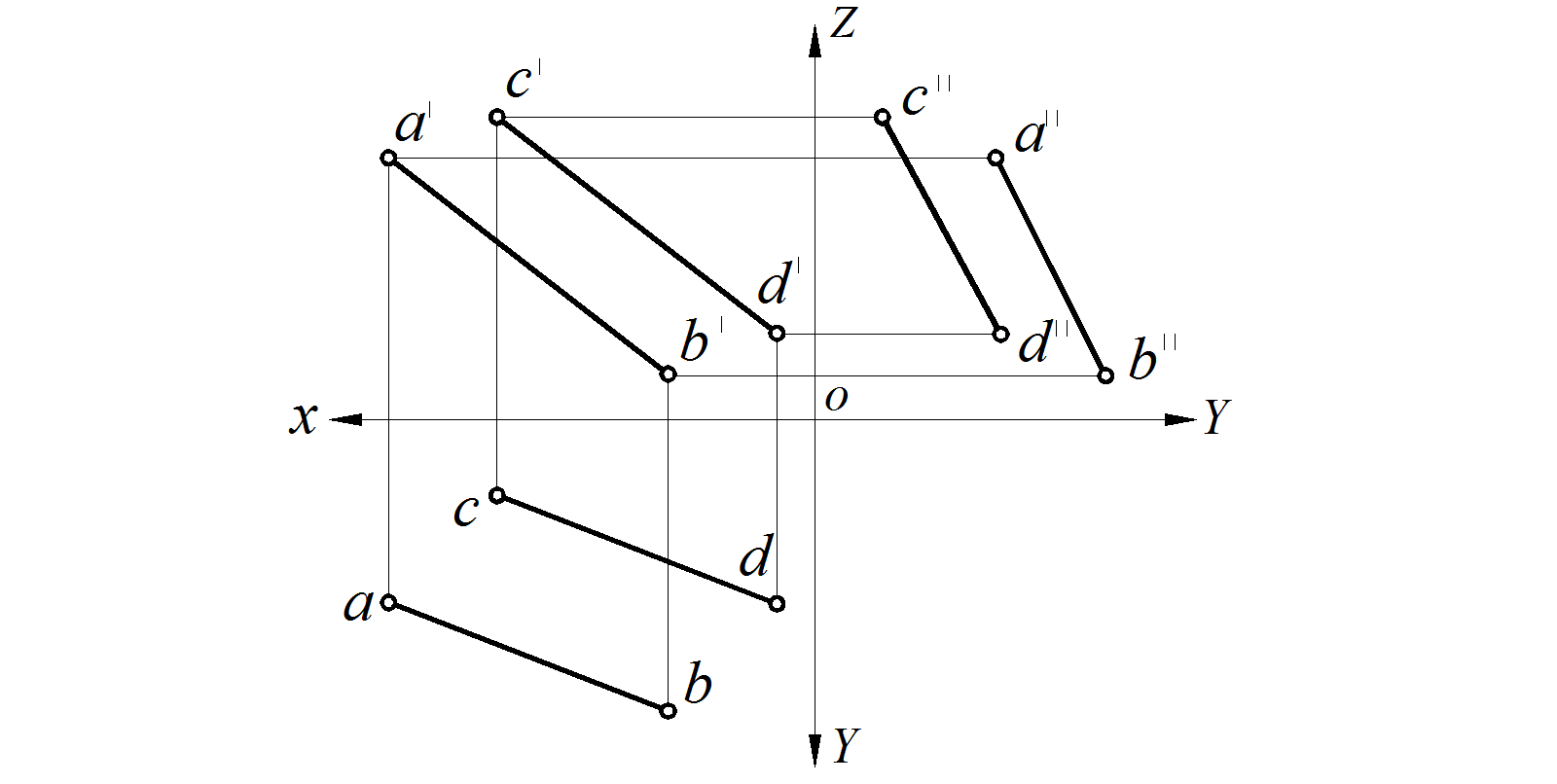
Рис. 31. Параллельные прямые АВ и С D

 

 

Скрещивающиеся прямые

Из курса средней школы известно, что скрещивающиеся прямые лежат в параллельных плоскостях, т. е. они в пространстве не пересекаются.

На чертеже проекции этих прямых могут пересекаться друг с другом, но, в отличие от чертежа пересекающихся прямых, точки пересечения одноименных проекций не лежат на одной линии связи.

 

Обычно на чертеже, изображающем скрещивающиеся прямые, определяют, какая из прямых находится выше или дальше другой от соответствующих плоскостей проекций, т. е. ближе к наблюдателю. В этом случае применяется метод конкурирующих (совпадающих) точек. Конкурирующие точки – это точки, лежащие на одном проецирующем луче.

На рис. 32 изображены проекции двух скрещивающихся прямых АВ и CD. На фронтальной проекции видим мнимое пересечение этих прямых, совпадающие точки 1 и 2 (1′ ≡ 2′), но, опуская из мнимой точки пересечения линию связи на горизонтальную проекцию, видно, что общей точки пересечения нет, а получаются две точки, принадлежащие этим прямым, лежащие на одной линии связи, но находящиеся в разных местах. И, судя по тому, что точка 1 находится дальше от оси Х, определяем по проекционной принадлежности, что прямая АВ находится дальше от фронтальной плоскости проекций, чем прямая CD. Точки 1 и 2 являются конкурирующими точками, при их совпадении принято невидимые (закрытые) точки заключать в скобки, поэтому точка 2, находящаяся за точкой 1, на фронтальной проекции заключена в скобки.

 

 

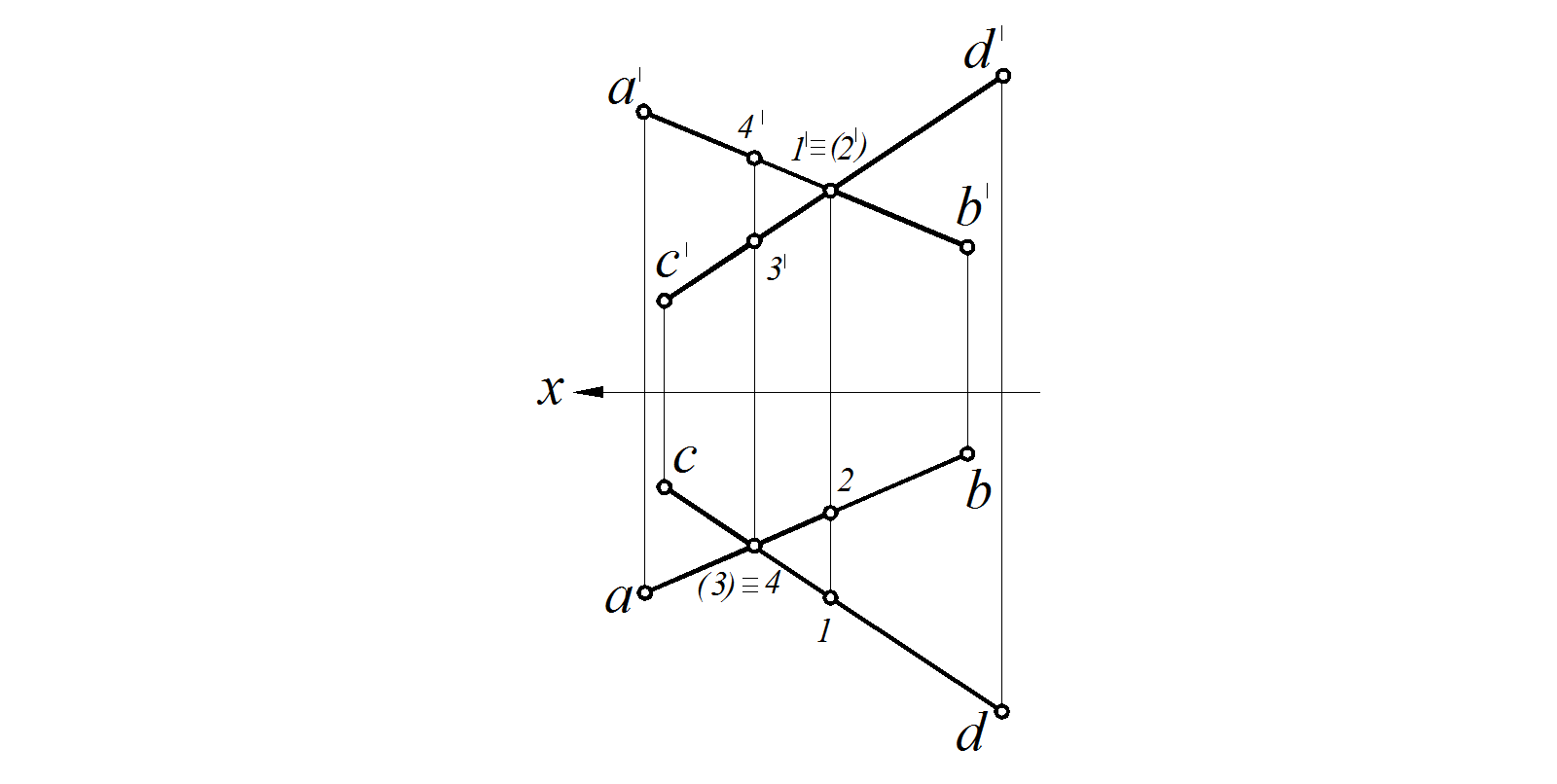
Рис. 32. Скрещивающиеся отрезки прямых АВ и С D:

точка 4 выше точки 3; точка 2 находится за точкой 1

 

Аналогичным образом можно рассматривать совпадающее положение точек 3 и 4 (3 ≡ 4) на горизонтальной плоскости проекций, представляющих мнимое пересечение проекций прямых АВ и CD. Далее, по проекционной принадлежности определив положение точек на фронтальной плоскости проекций, можно заключить, что точка 4 находится выше точки 3 и, значит, дальше от горизонтальной плоскости проекций. А так как точка 4 принадлежит прямой АВ, то и прямая АВ находится выше прямой CD.

Точка 3 находится ниже точки 4 и закрывается ею, поэтому ее горизонтальная проекция заключена в скобки, как невидимая.

Следует отметить, что для определения взаимного положения прямых общего положения достаточно рассмотреть их две любые проекции. Третью проекцию, без необходимости, строить необязательно.

Для определения взаимного положения прямых уровня одна из рассматриваемых проекций должна быть та, где прямая проецируется в натуральную величину.

Задача. Определить взаимное положение прямых А B и CD (рис. 33).

Решение

1. Анализируем заданный чертеж:

1.1. Взаимных положений прямых возможны 3 варианта: пересечение, параллельность и скрещивание. Так как заданные проекции прямых не параллельны друг другу, следовательно, заданные прямые не параллельны друг другу в пространстве.

1.2. Рассмотрим положение в пространстве каждой из заданных прямых. Прямая CD занимает общее положение. Прямая АВ занимает частное положение – является профильной прямой уровня. На профильной проекции прямая будет проецироваться в натуральную величину. Следовательно, для определения взаимного положения прямых АВ и CD надо построить профильные проекции этих прямых.

 

 

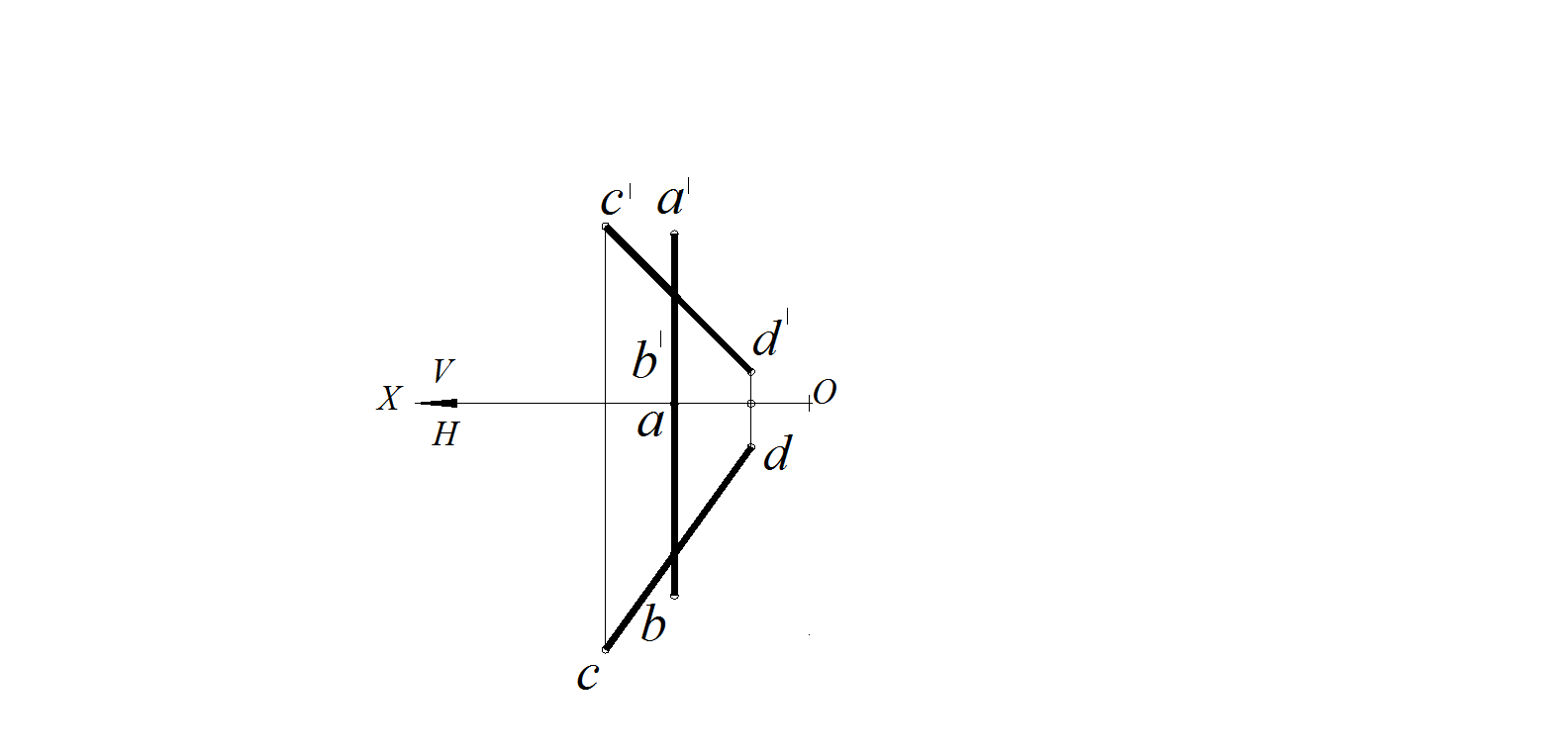
Рис. 33. Условие задачи

 

 

 

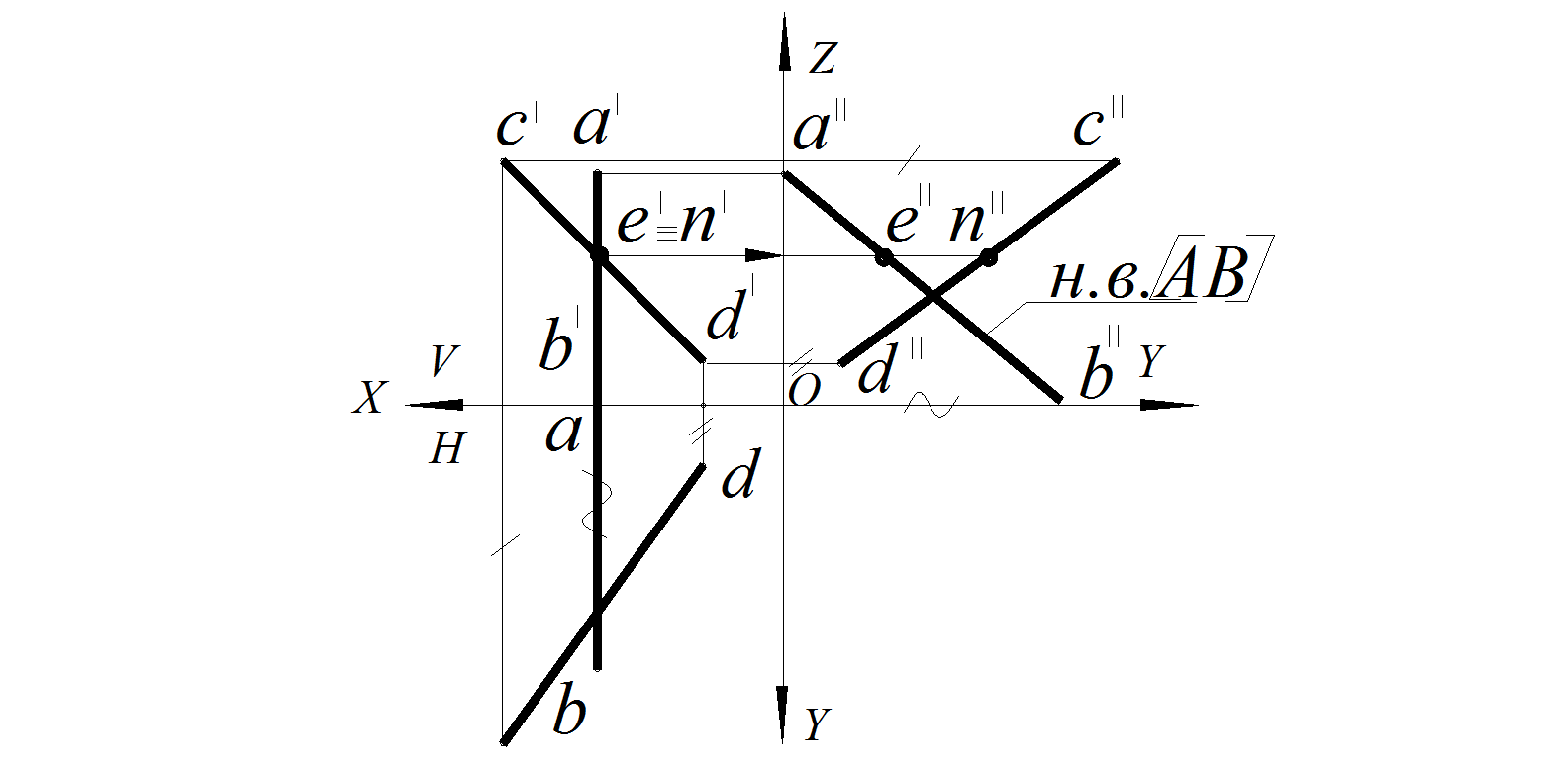
Рис. 34. Решение задачи

 

2. Как видно на рис. 34, мнимая точка пересечения прямых распадается на две точки на профильной проекции – Е и N. Следовательно, эти прямые скрещиваются.

 

Проекции плоских углов

Плоскостей проекций

 

Проецирующие плоскости

1. Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций Н (рис. 40–41): плоскость ΔАВС ⊥ Н; горизонтальная проекция этой плоскости – прямая а b с, совпадающая с горизонтальным следом, который располагается под углом к оси Х, соответствующим углу наклона этой плоскости к фронтальной плоскости проекций V – ∠β.

 

а

б

 

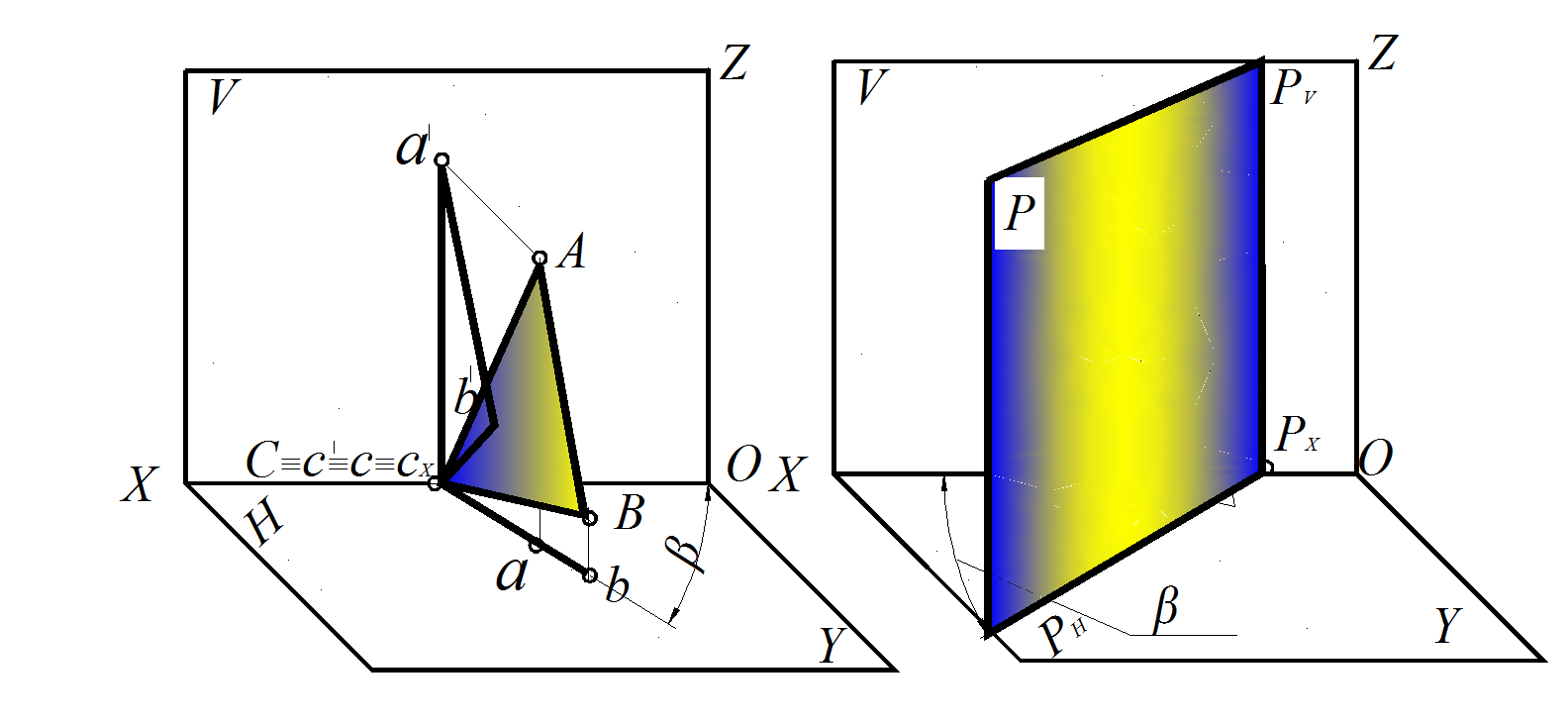
Рис. 40. Горизонтально проецирующая плоскость, пространственная модель:

а – заданная ΔАВС; б – следами плоскости Р

 

  

б

а

 

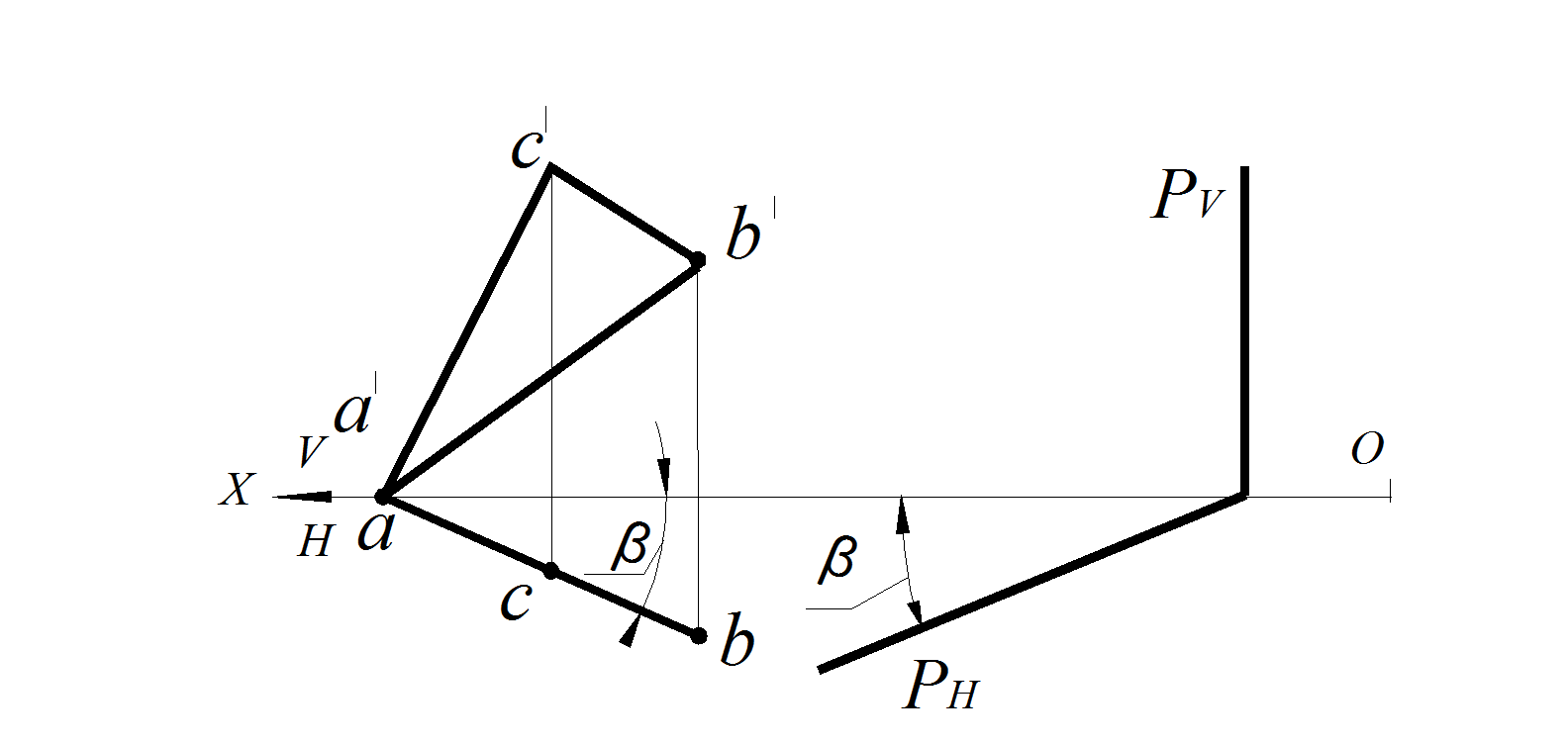
Рис. 41. Горизонтально проецирующая плоскость на эпюре:

а – заданная ΔАВС; б – следами плоскости Р

2. Фронтально проецирующая плоскость перпендикулярна плоскости проекций V (рис. 42–43): плоскость ∆ABC ⊥ V ; фронтальная проекция этой плоскости – прямая, совпадающая с фронтальным следом, который располагается под углом к оси Х, соответствующим углу наклона этой плоскости α к горизонтальной плоскости проекций Н.

а

б

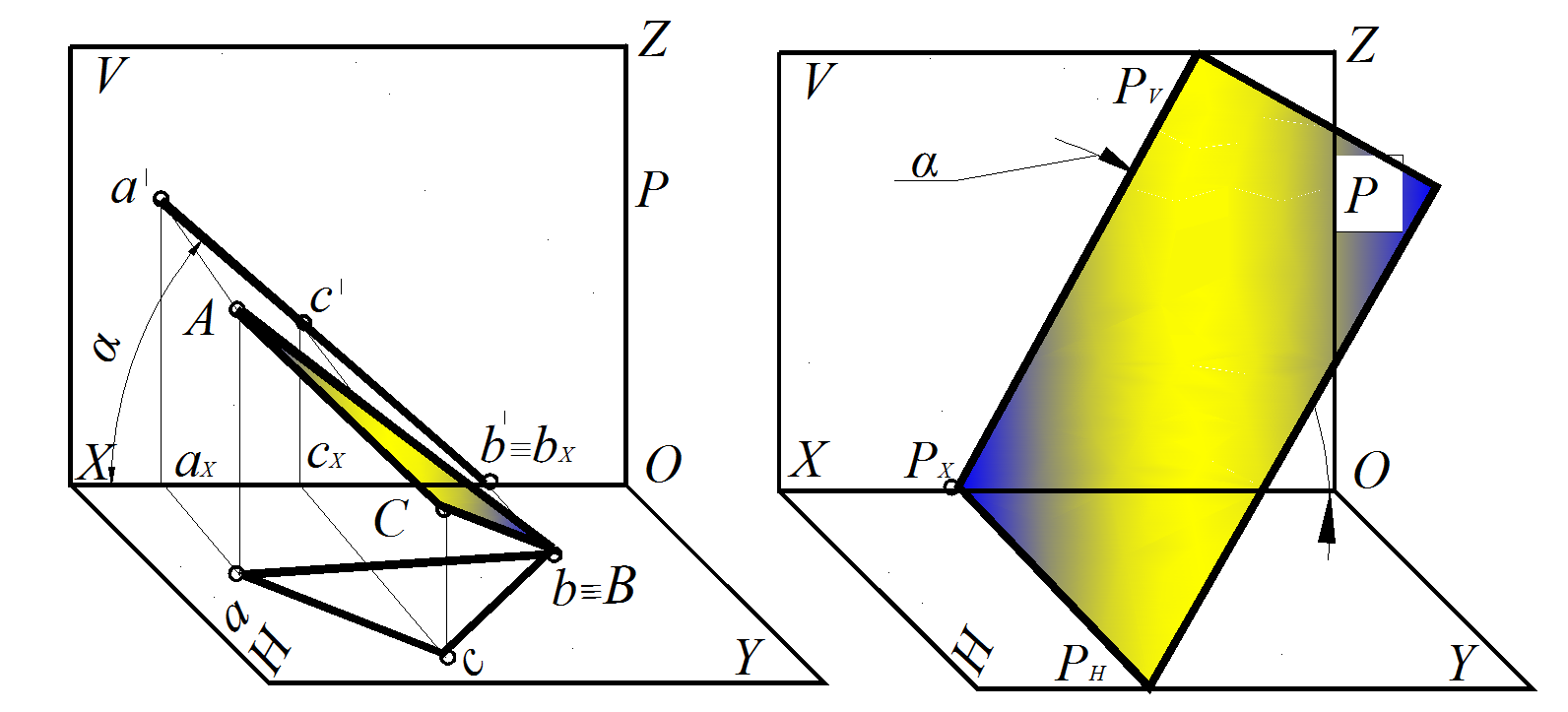
Рис. 42. Фронтально проецирующая плоскость в пространственной модели:

а – заданная ΔАВС; б – следами плоскости Р

б

а

 

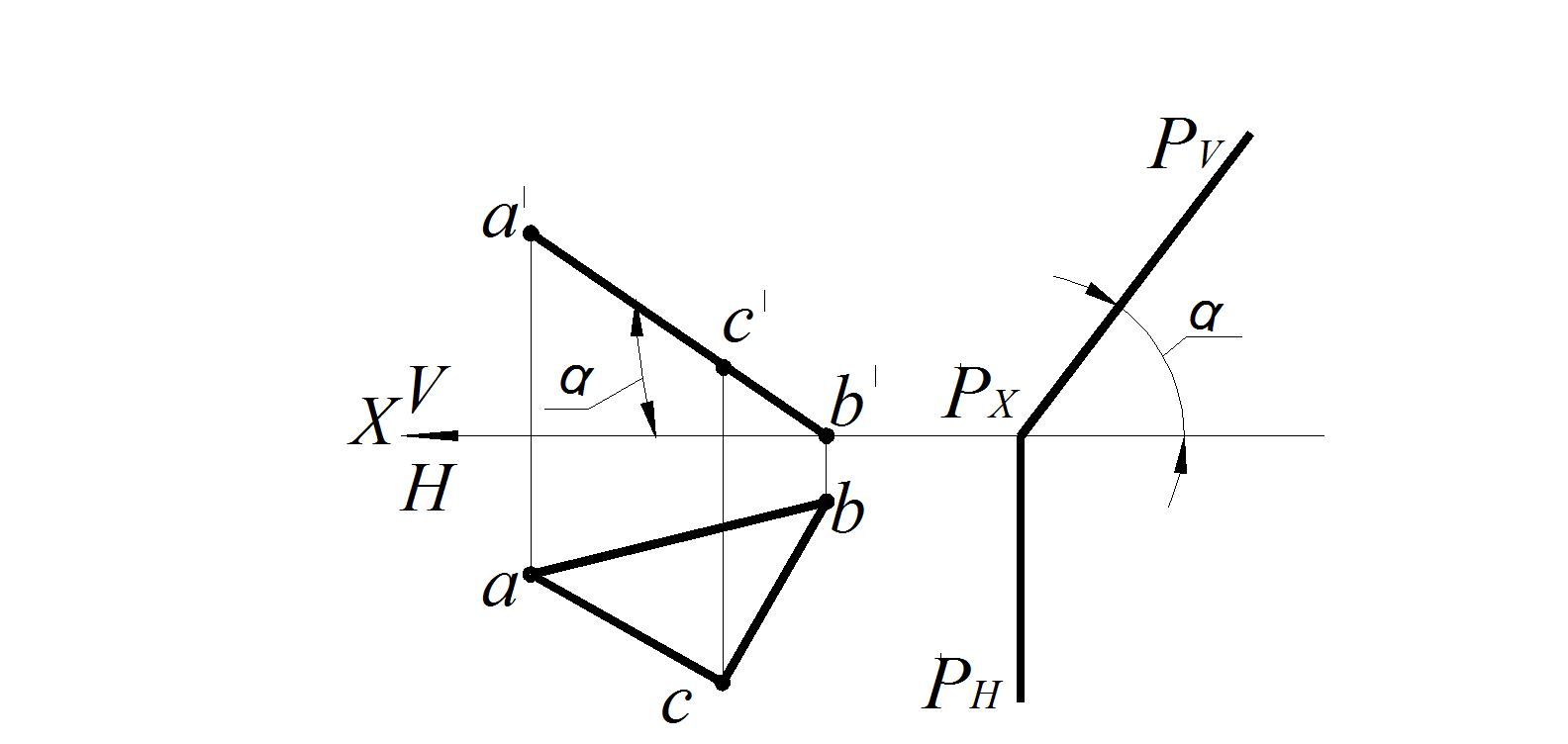
Рис. 43. Фронтально проецирующая плоскость на эпюре:

а – заданная ΔАВС; б – следами плоскости Р

3. Профильно проецирующая плоскость перпендикулярна плоскости W (рис. 44–45): ΔABC ⊥ W; профильная проекция – прямая, совпадающая со следом Р _W, который располагается под углом к оси Z, соответствующим углу наклона этой плоскости β к фронтальной плоскости проекций V, под углом к оси y, соответствующим углу наклона этой плоскости α к горизонтальной плоскости проекций Н.

 

 

 

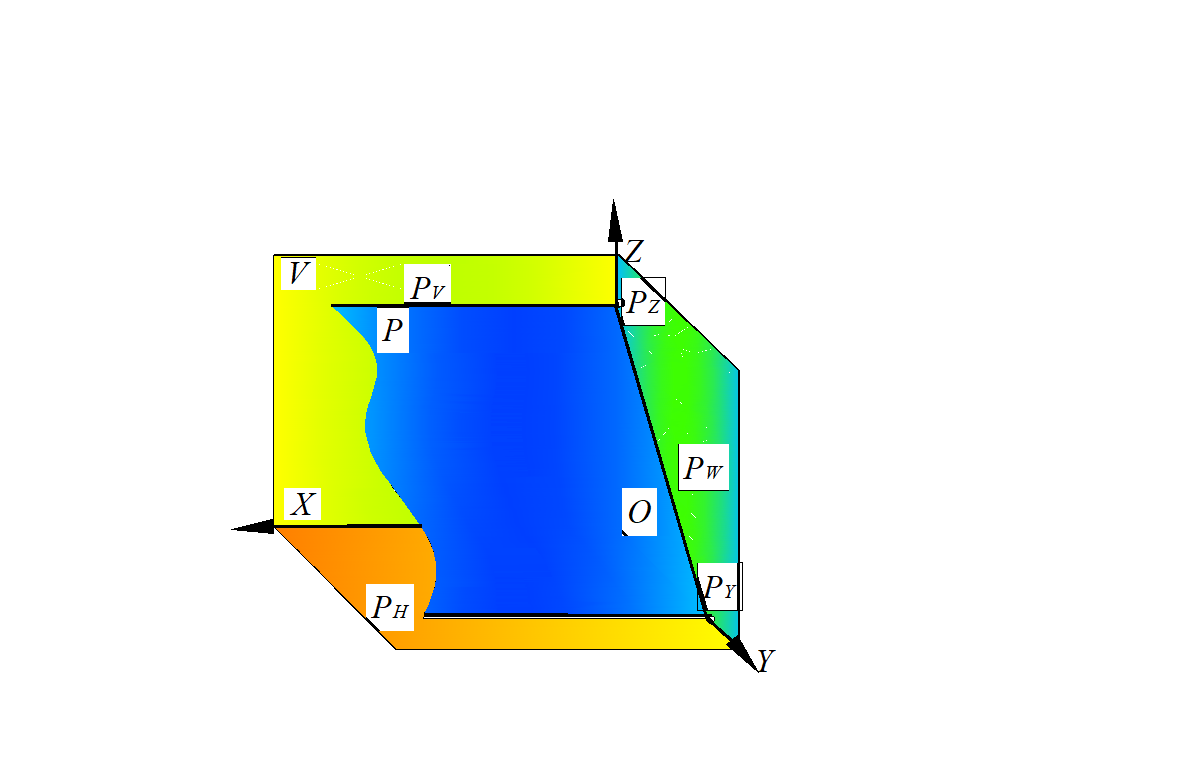
Рис. 44. Профильно проецирующая плоскость, заданная следами, в пространственной модели

 

б

а

 

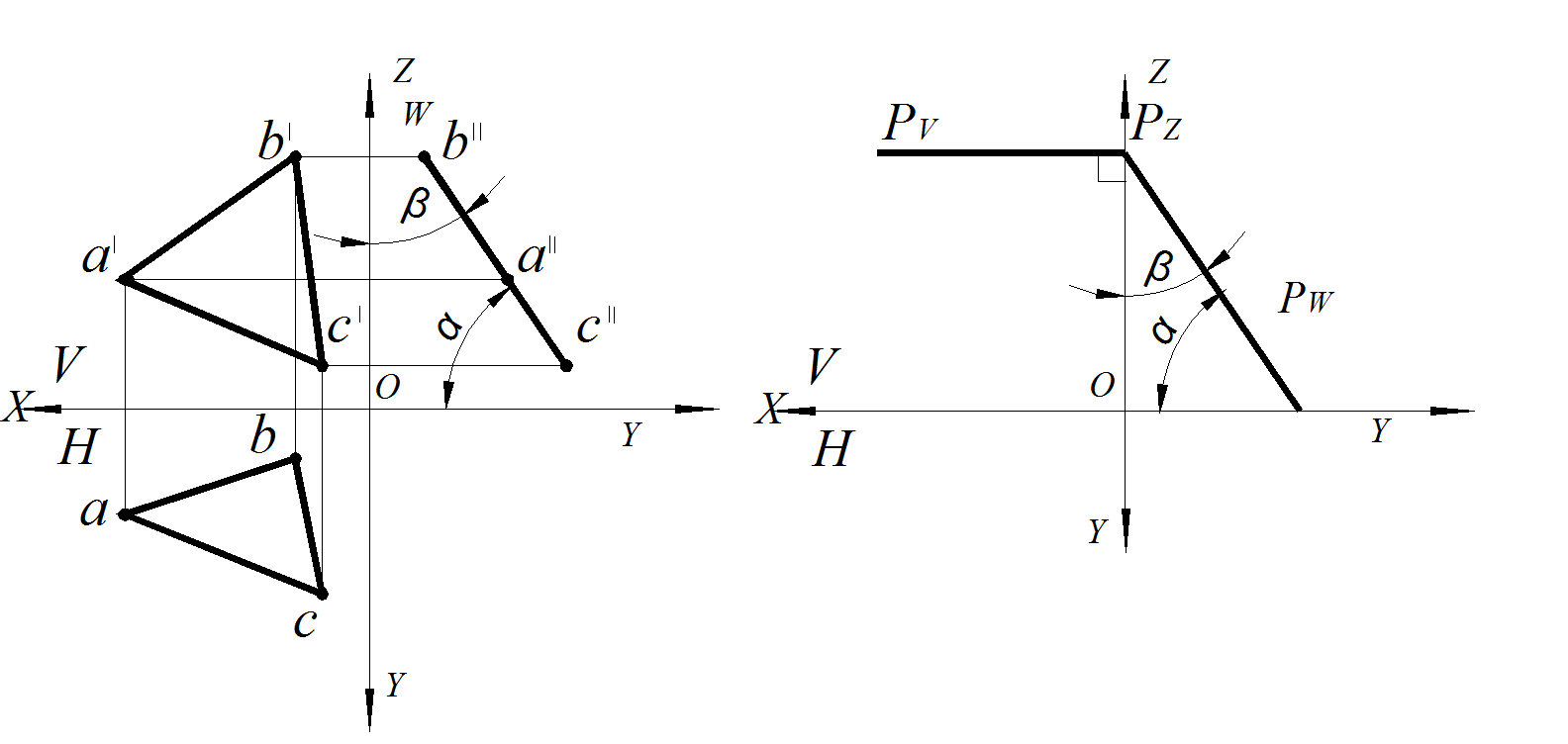
Рис. 45. Профильно проецирующая плоскость:

а – заданная ΔАВС; б – заданная следами плоскости

 

Свойства проецирующих плоскостей и их чертежей заключаются в следующем: плоскость проецируется в виде прямой линии на ту плоскость проекций, которой она перпендикулярна, причем угол наклона этой прямой определяет угол наклона плоскости к соответствующей плоскости проекций. Следовательно, все геометрические элементы: точки, прямые линии, плоские фигуры, лежащие в проецирующей плоскости, проецируются на эту плоскость проекций в прямую линию.

 

Плоскости уровня

Плоскость уровня – плоскость, параллельная какой-либо плоскости проекций (или перпендикулярная двум плоскостям проекций).

1. Горизонтальная плоскость уровня – параллельна горизонтальной плоскости проекций Н (рис. 46).

Свойства чертежа плоскости горизонтальной плоскости уровня:

– фронтальная проекция плоскости – прямая, параллельная оси Х;

– на горизонтальной проекции все элементы плоскости – прямые, углы, проецируются без искажения.

2. Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций V (рис. 47).

Свойства чертежа плоскости фронтальной плоскости уровня:

– горизонтальная проекция плоскости – прямая, параллельная оси Х;

– на фронтальной проекции все элементы плоскости – прямые, углы, проецируются без искажения.

3. Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций W (рис. 48).

 

а

б

 

 

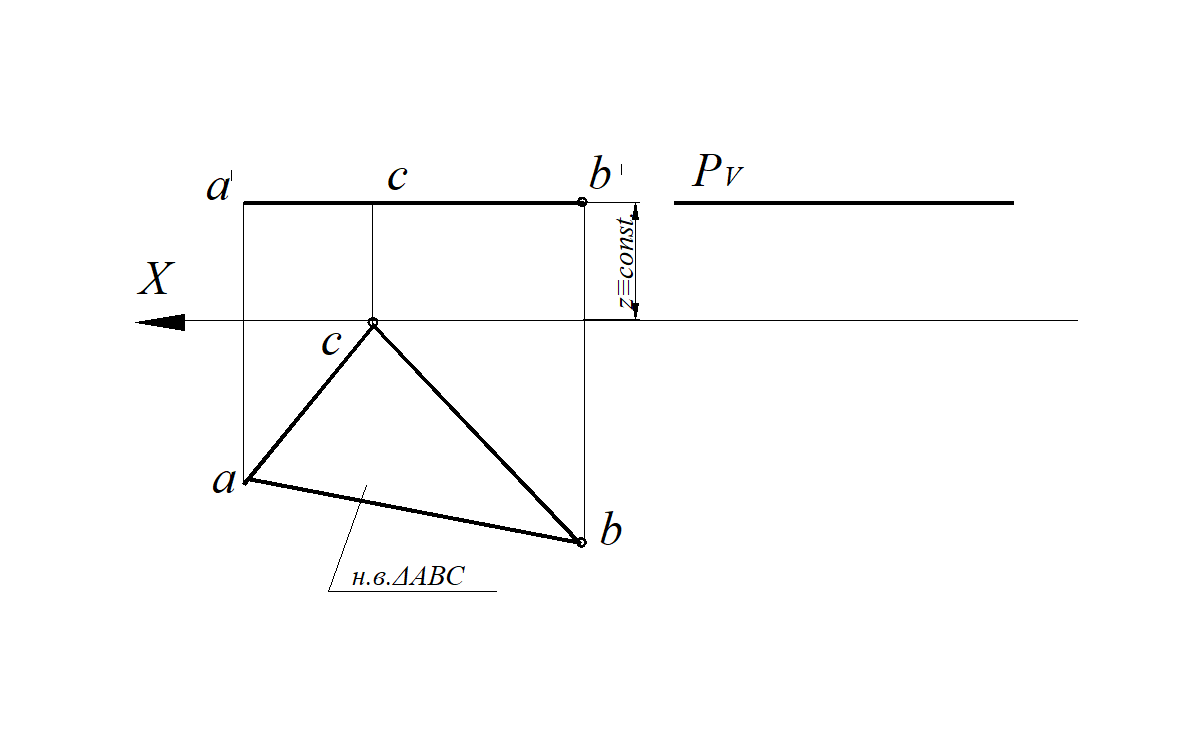
Рис. 46. Горизонтальная плоскость уровня:

а – заданная ΔАВС; б – следами плоскости Р

 

 

 

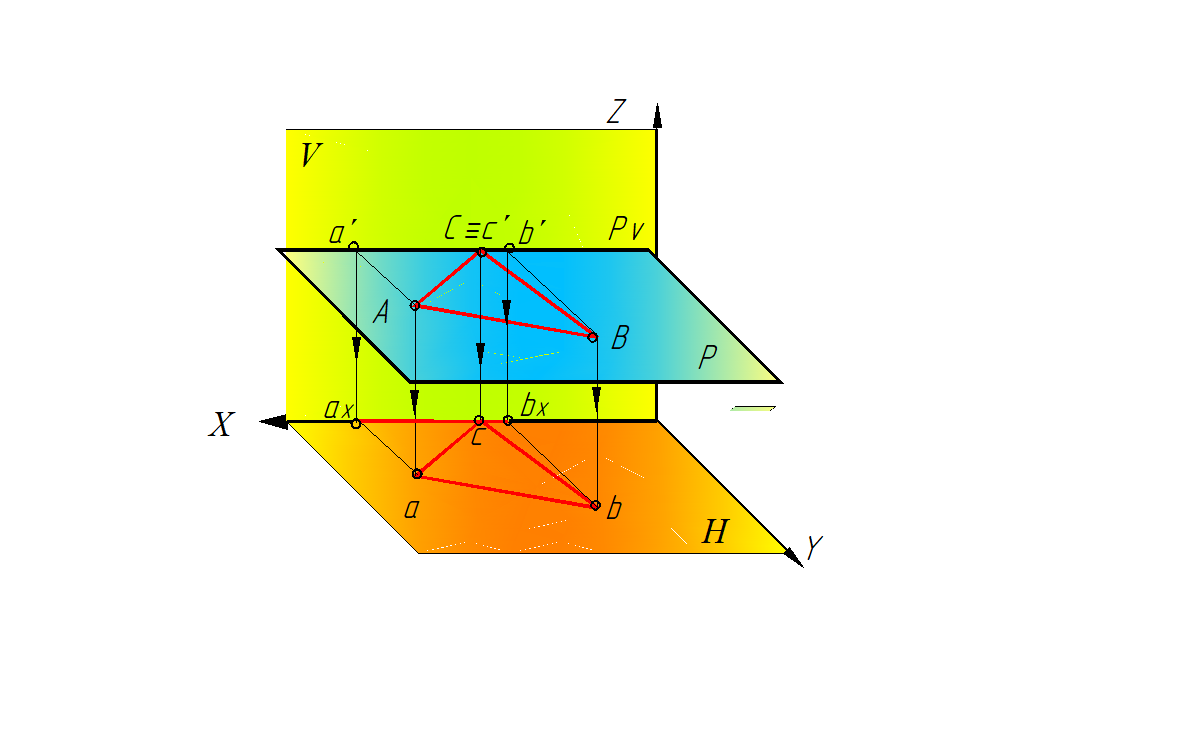
Рис. 47. Горизонтальная плоскость уровня-

пространственная модель

 

 

 

 

а

б

 

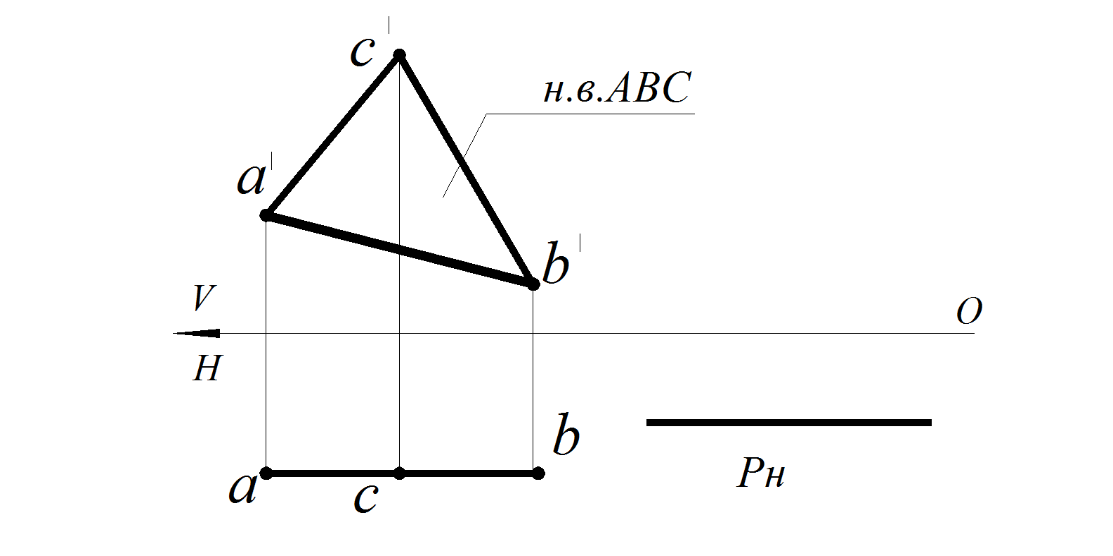
Рис. 48. Фронтальная плоскость уровня:

 а – заданная ΔАВС; б – следами плоскости Р

 

 

 

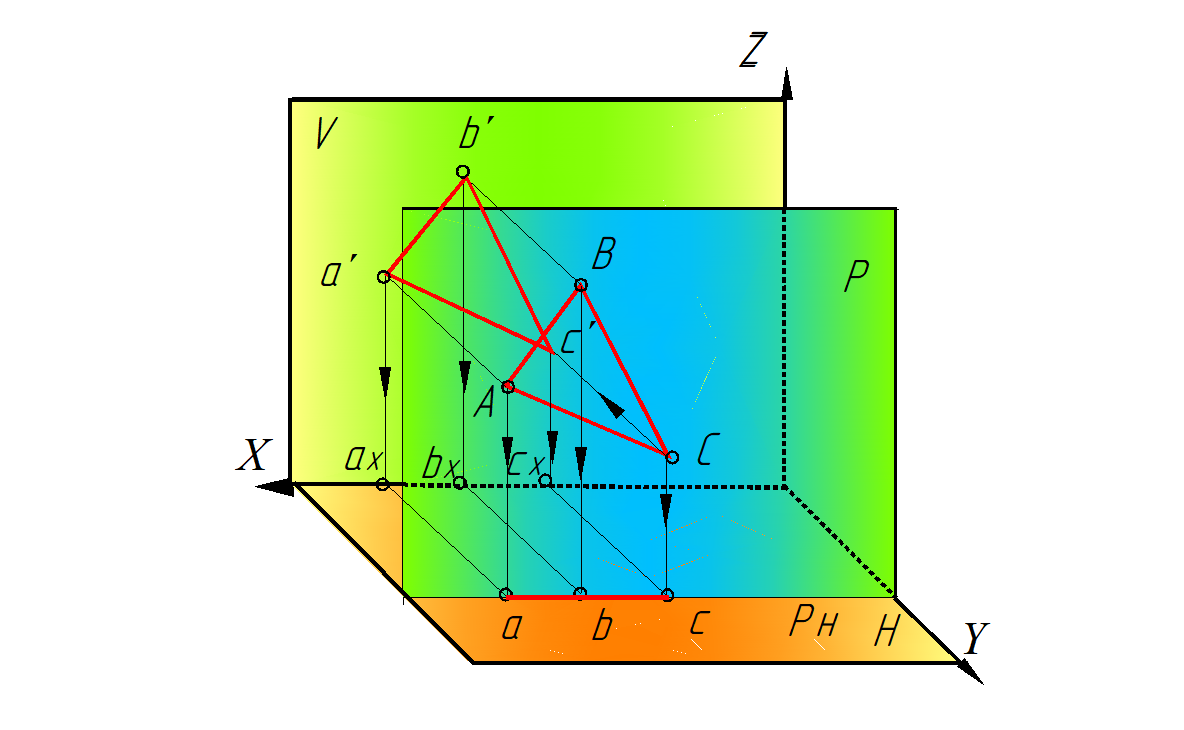
Рис. 49. Фронтальная плоскость уровня-

пространственная модель

 

 

 

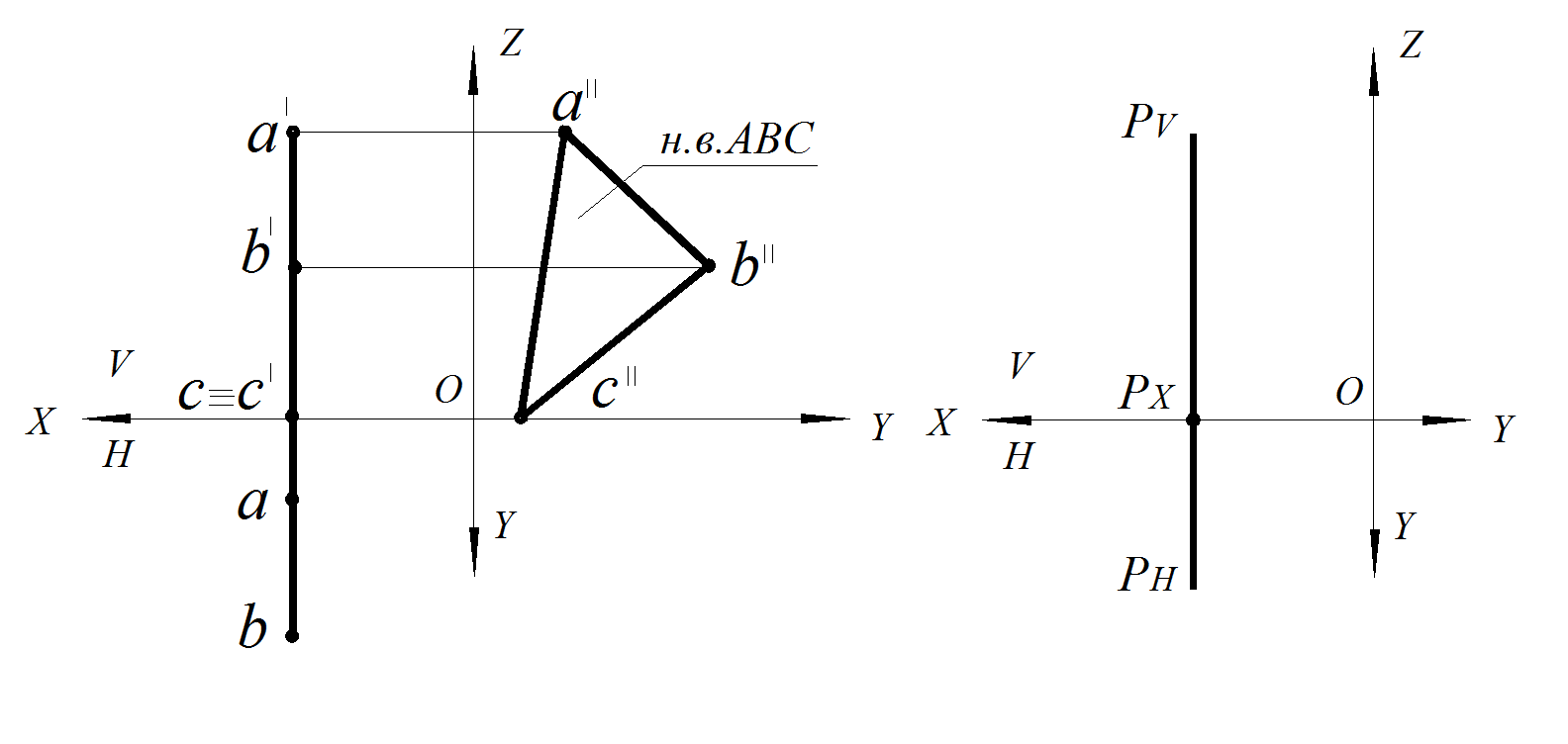
Рис.50. Профильная плоскость уровня:

а – плоскостью ΔАВС; б – заданная следами плоскости Р

 

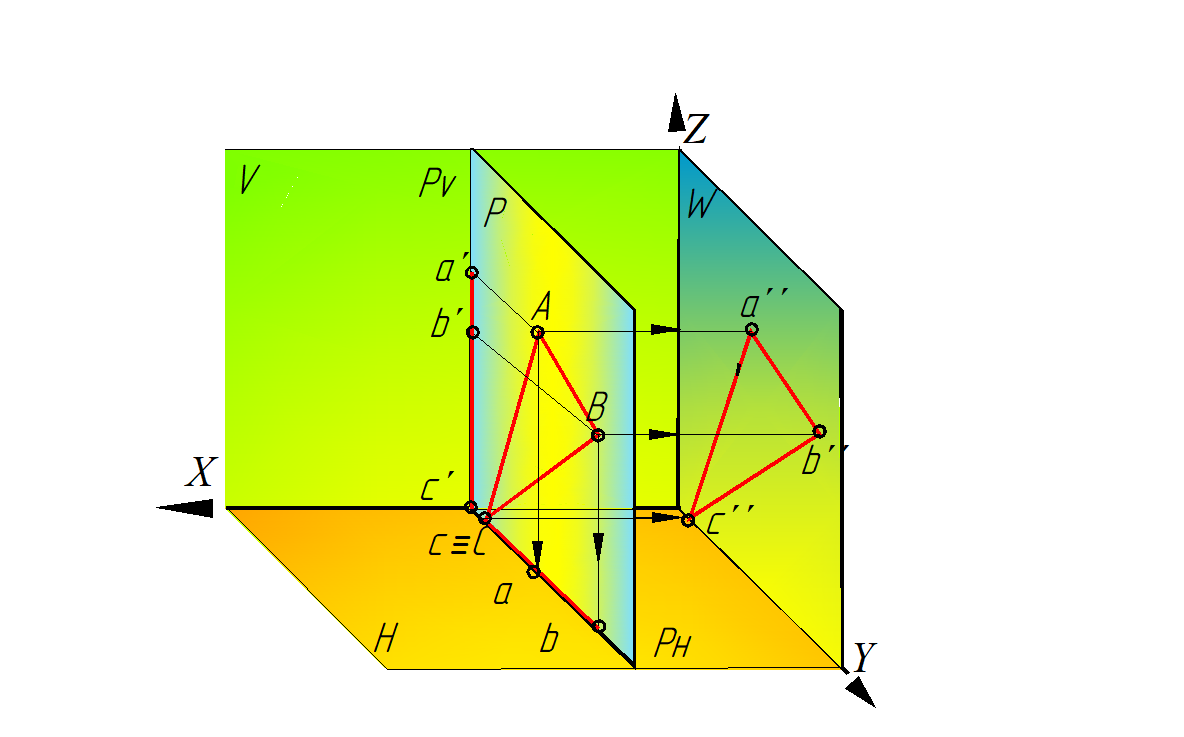
Рис. 51. Профильная плоскость уровня-

пространственная модель

 

Свойства чертежа плоскости профильной плоскости уровня:

а) горизонтальная проекция плоскости – прямая, параллельная оси Y и фронтальная проекция плоскости – прямая, параллельная оси Z;

б) на профильной проекции все элементы плоскости – прямые, углы, проецируются без искажения.

 

Следовательно, свойства чертежей плоскостей уровня таковы:

Геометрические элементы, лежащие в плоскости уровня (отрезки, плоские фигуры), проецируются в натуральную величину на ту плоскость проекций, которой они параллельны, а на две другие плоскости – в виде прямых линий, которые совпадают со своими одноименными следами.

 

Плоскость общего положения

Плоскость общего положения – это плоскость, не перпендикулярная ни одной плоскости проекций (рис. 52).

Свойство чертежа:

1. Ни одна из проекций плоскости общего положения не является прямой.

2. Фигура, лежащая в плоскости общего положения, отображается на плоскости проекций с искажением

 

.

а

в

б

 

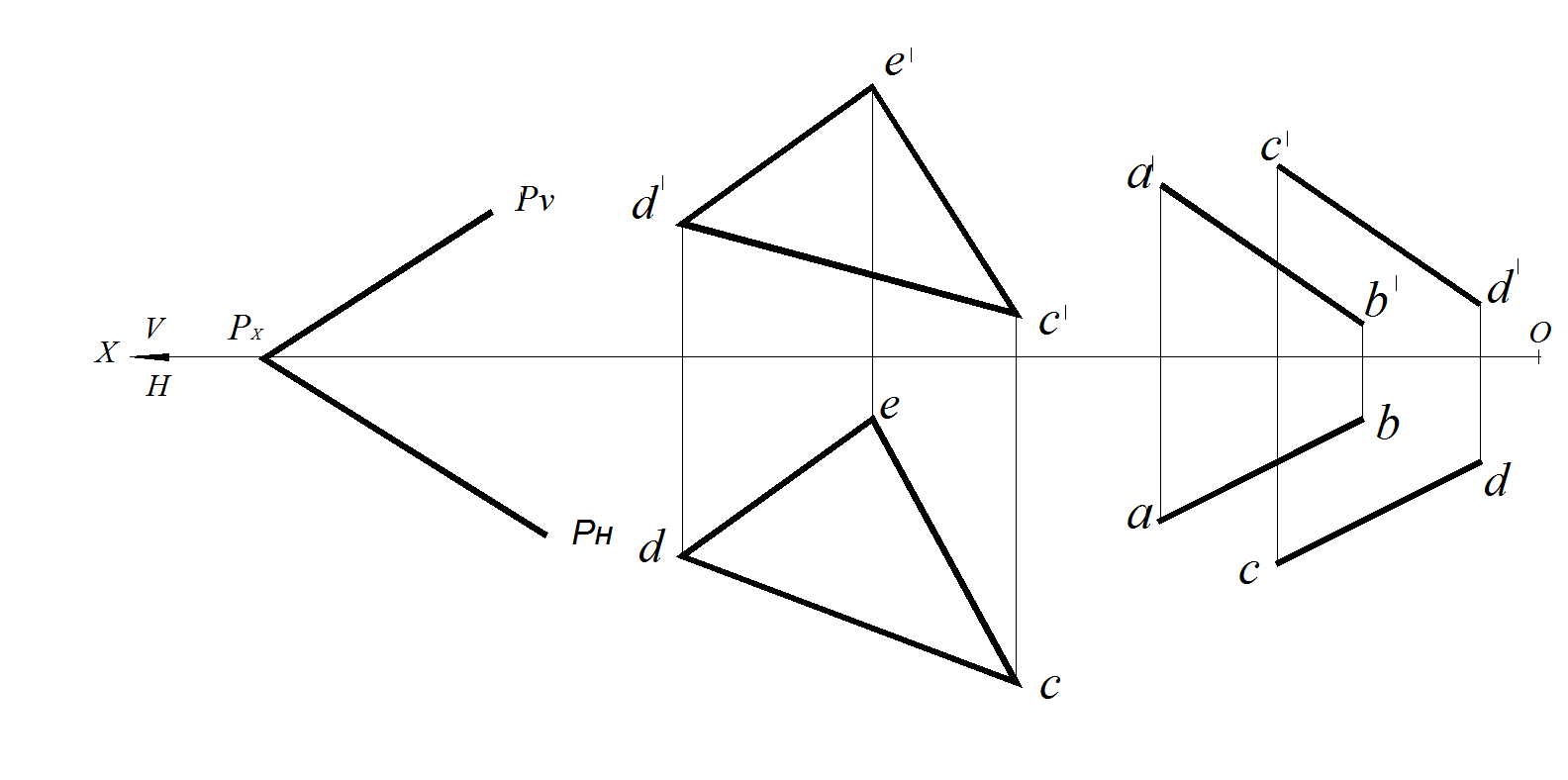
Рис. 52. Плоскость общего положения:

а – заданная следами плоскости Р; б – заданная ΔАВС; в – параллельными прямыми АВ и С D

 

 

Прямая и точка в плоскости

Построение проекций точки и прямой, принадлежащих заданной плоскости, выполняется на основании известных аксиом:

1. Через две любые различные точки можно провести только одну прямую.

2. Если две точки прямой принадлежат плоскости, то и все точки этой прямой принадлежат заданной плоскости.

Решение этих задач основывается на известных положениях геометрии:

1. Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.

2. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости, или через одну точку этой плоскости параллельно прямой, лежащей в этой плоскости или ей параллельной.

 

По свойству принадлежности точки прямой – ее проекции лежат на одноименных проекциях прямой, принадлежащей плоскости.

 

Задача.

Построить в плоскости, заданной треугольником D ЕС, недостающие проекции точки А и точки В, принадлежащих плоскости заданного треугольника (рис. 54).

 

          

 

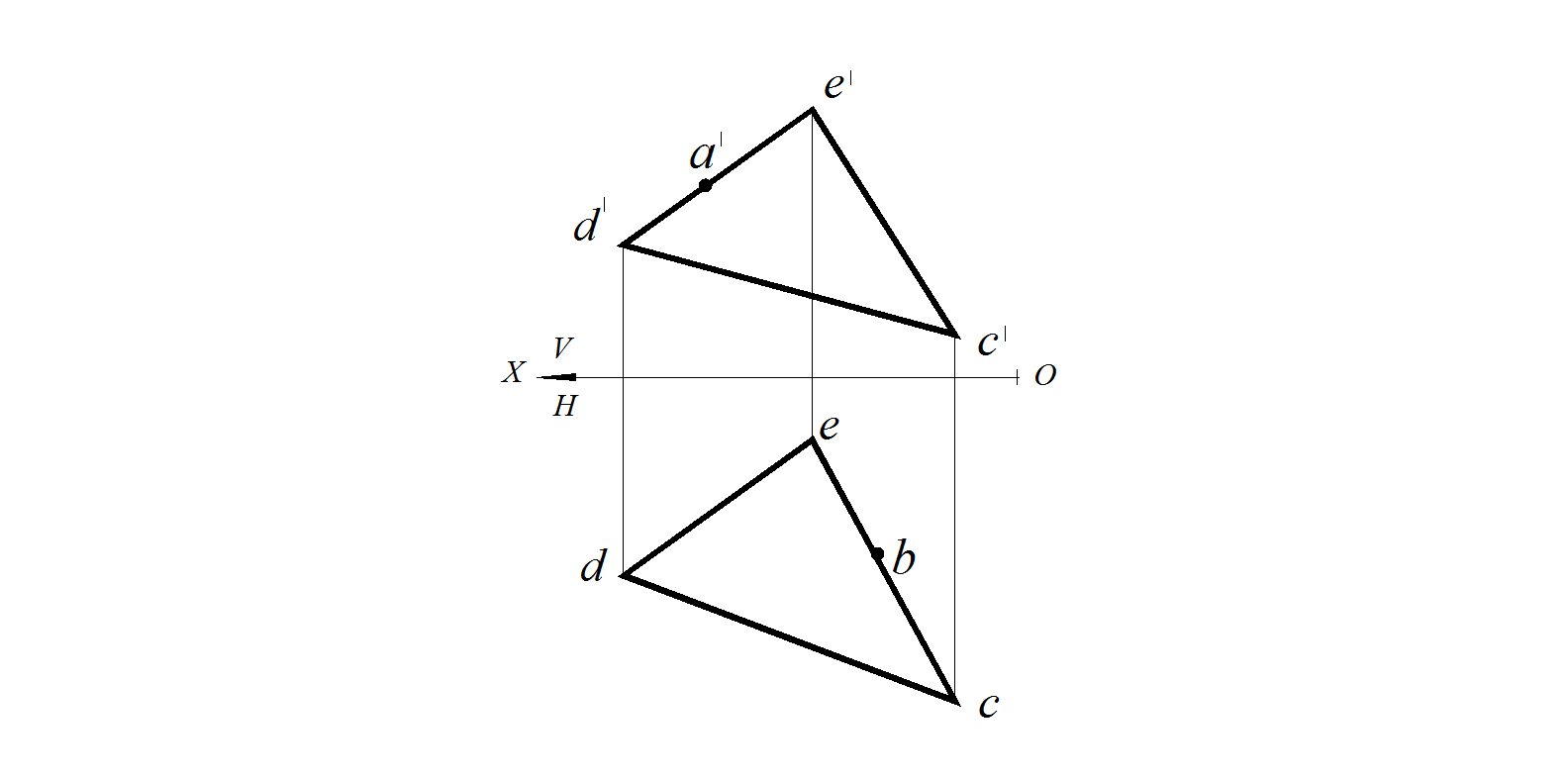
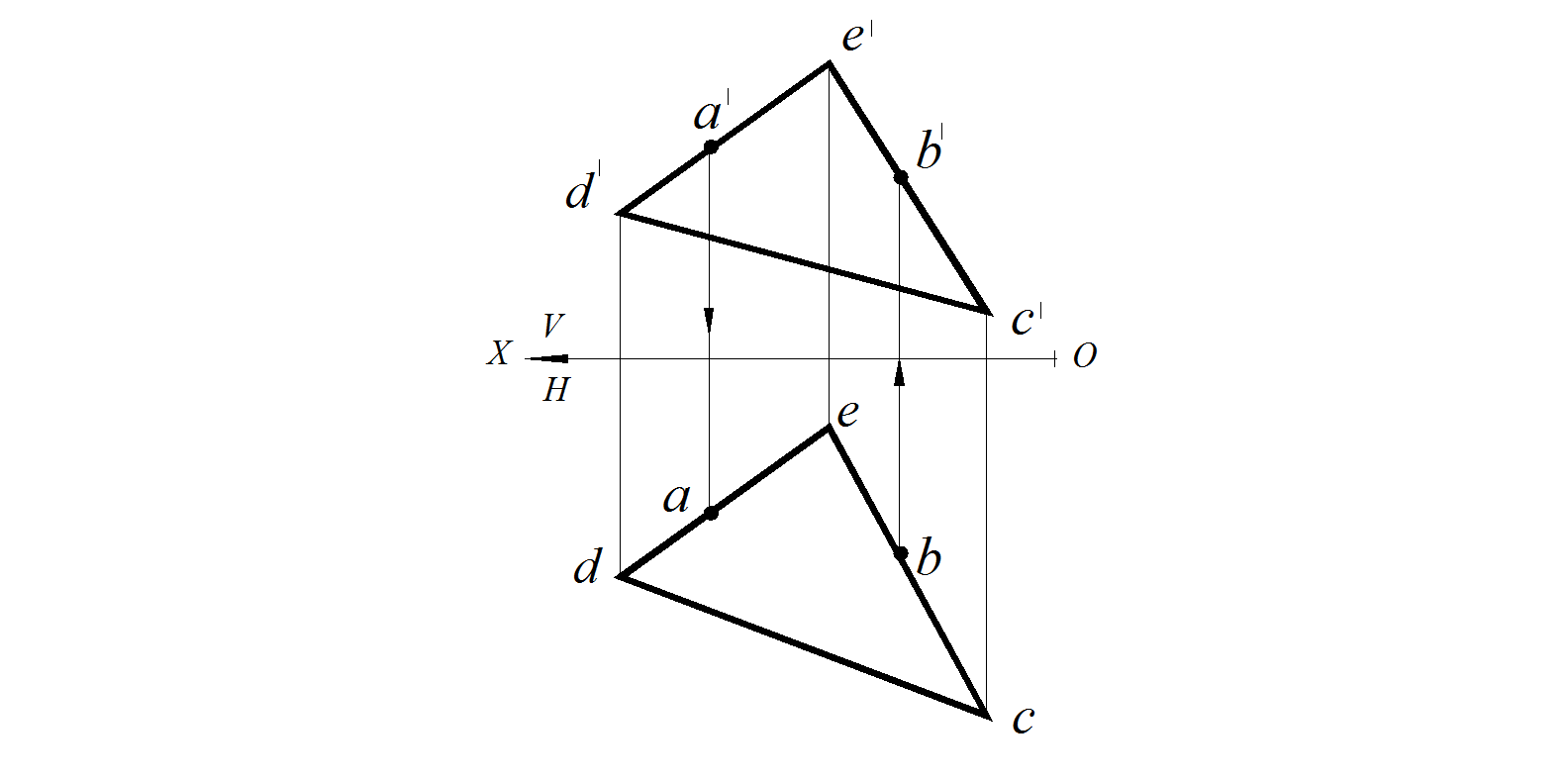
 Рис. 54. Условие задачи             Рис. 55. Построение в плоскости точки

 

Решение:

Анализируя графическое условие задачи, видим, что точка А принадлежит прямой D Е. Следовательно, по свойству принадлежности, ее горизонтальная проекция тоже принадлежит горизонтальной проекции прямой DE . Проводим линию связи из фронтальной проекции точки А до пересечения с горизонтальной проекцией прямой D Е. Полученная точка будет горизонтальной проекцией точки А. Аналогично строим фронтальную проекцию точки В (рис. 55).

 

Задача.

Задача.

Определить принадлежность точки А плоскости, заданной треугольником DFE (рис. 58).

Решение:

Для проверки принадлежности точки плоскости используют вспомогательную прямую, принадлежащую плоскости. Предполагают, что заданная точка принадлежит заданной плоскости. Следовательно, она принадлежит любой прямой, лежащей в заданной плоскости. Поэтому точку А «привязываем» к плоскости треугольника прямой. Для этого на горизонтальной проекции проводим прямую через точку а и точку b . Отмечаем точку пересечения проведенной прямой со стороной dc – точку b. Строим фронтальную проекцию полученной прямой b ' e '. Анализируя чертеж, видим, что фронтальная проекции точки А не принадлежит прямой ВЕ. Следовательно, заданная точка А не принадлежит заданной плоскости треугольника DEC. (рис. 64).

     

                       

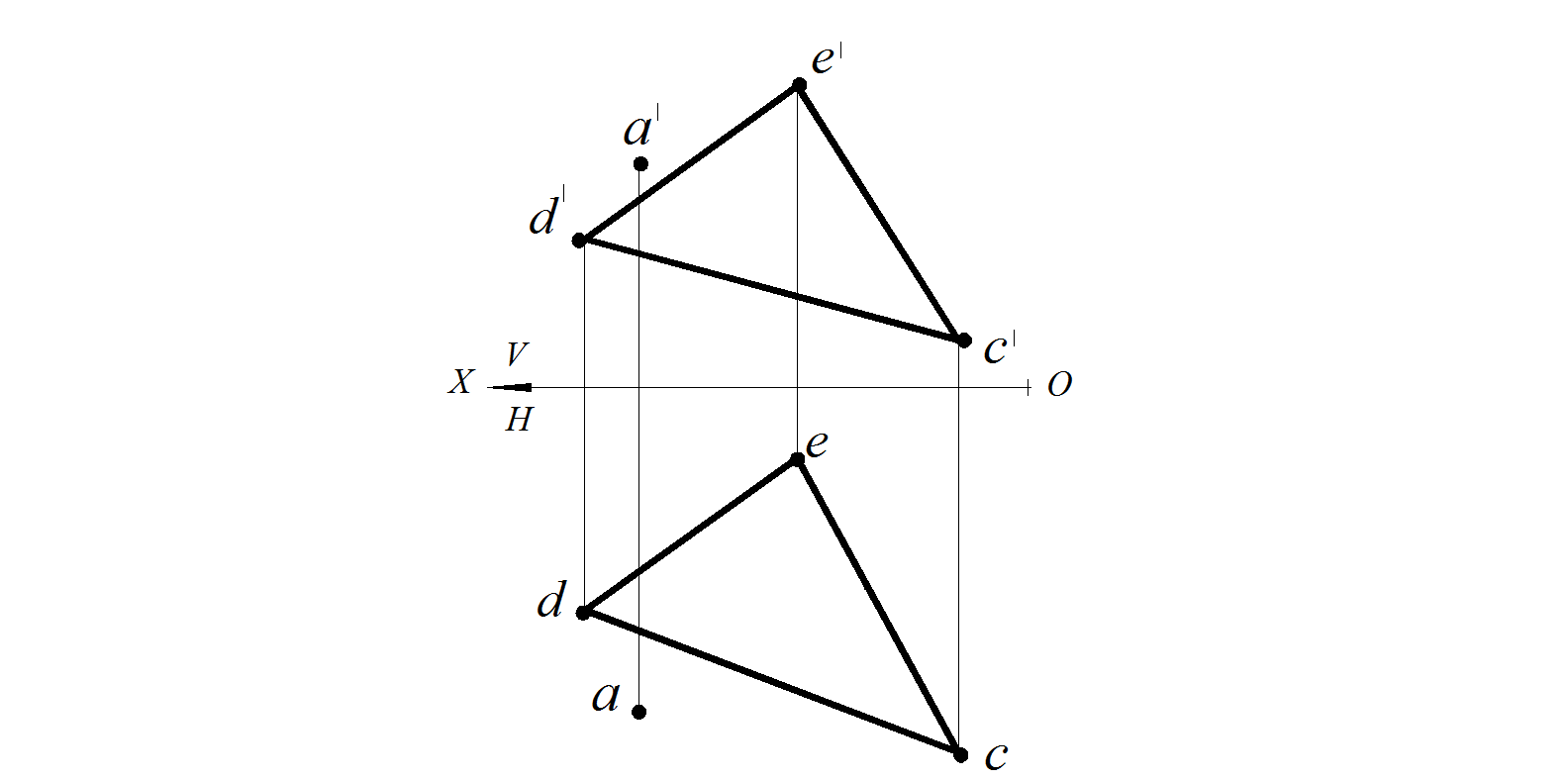
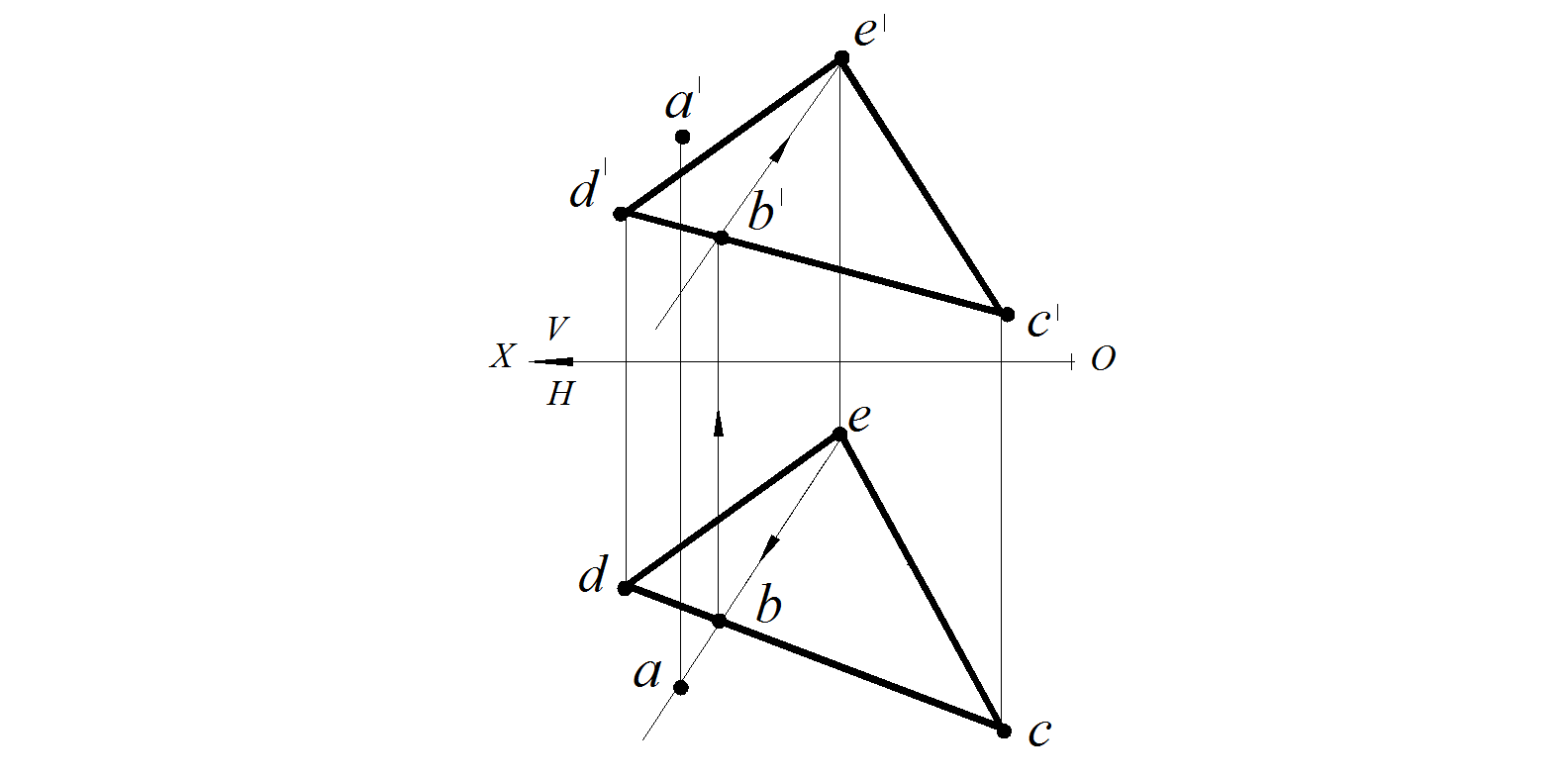
          Рис. 58. Условие задачи                  Рис. 59. Проверка принадлежности точки плоскости

                                                                                                    

 

Особые линии плоскости

Особые линии плоскости

 Прямые, занимающим особое положение в плоскости:

1. Линии уровня плоскости.

2. Линии наибольшего наклона плоскости к плоскостям проекций.

 

Линии уровня плоскости

 

Линии уровня плоскости – прямые, лежащие в заданной плоскости и параллельные плоскостям проекций: горизонтали, фронтали, профильные прямые.

Горизонталь плоскости – прямая, лежащая в заданной плоскости и параллельная плоскости проекций Н. Следует запомнить, что все горизонтали одной и той же плоскости параллельны между собой.

 Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости, горизонтальный след плоскости является нулевой горизонталью плоскости. Чтобы построить горизонталь в плоскости Р, заданной следами, надо на фронтальной проекции Р _V отметить точку d ' – фронтальную проекцию следа горизонтали (рис. 60, а). Через нее проводим фронтальную проекцию горизонтали параллельно оси х. На оси х находим горизонтальную проекцию d. Прямая, проведенная из точки d параллельно следу Р_Н плоскости, представляет горизонтальную проекцию горизонтали.

На рис. 60, б проекции горизонтали проведены через проекции точки D и точки 1 прямой ЕС плоскости, заданной треугольником С DE . Построение горизонтали всегда начинают с фронтальной проекции d '1', которая параллельна оси Х. По свойству принадлежности находят горизонтальную проекцию точки 1 и проводят горизонтальную проекцию горизонтали.

 

а

б

 

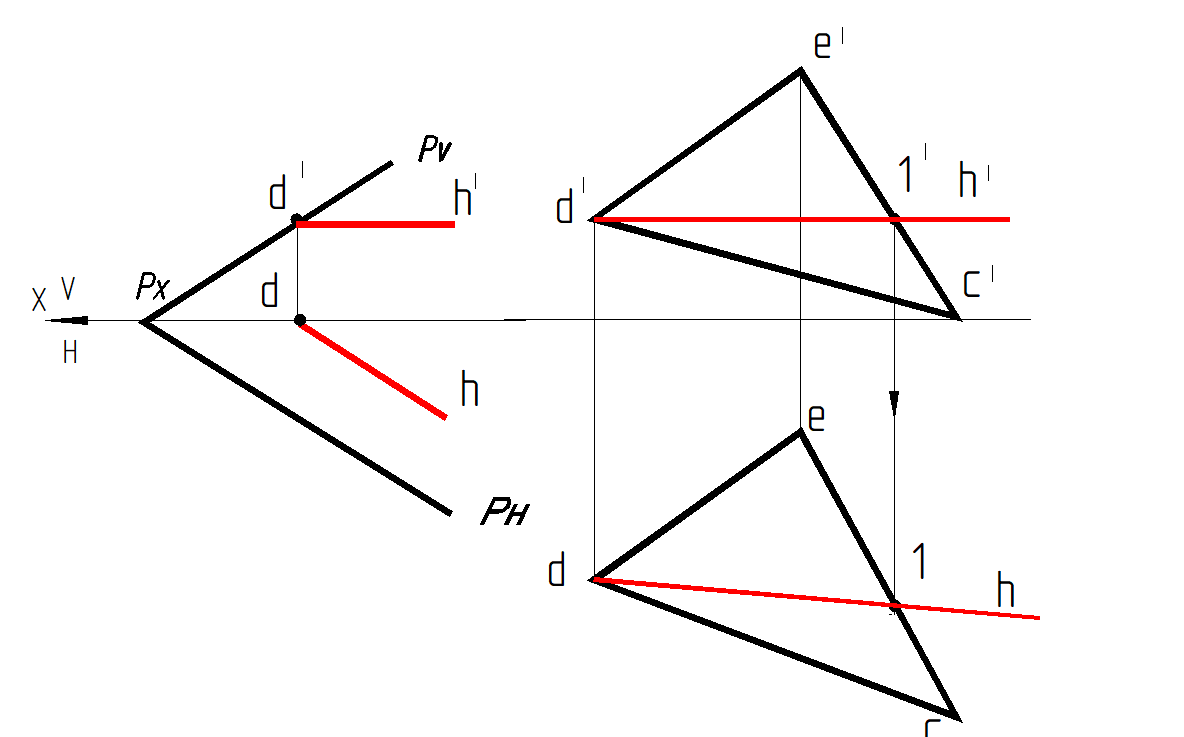
Рис. 60. Горизонталь плоскости:

а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆С DE

 

Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости проекций V (рис. 61).

Построение фронтали и профильных прямых выполняется аналогично построению горизонтали, опираясь на известные свойства проекций линий уровня и свойство принадлежности, и начинают его с той проекции, которая параллельна соответствующей проекционной оси. Все фронтали одной и той же плоскости параллельны между собой. То же самое можно сказать и о профильных прямых уровня плоскости.

Профильная прямая уровня плоскости – это прямая, лежащая в данной плоскости и параллельная профильной плоскости проекций (рис. 62).

 

б

а

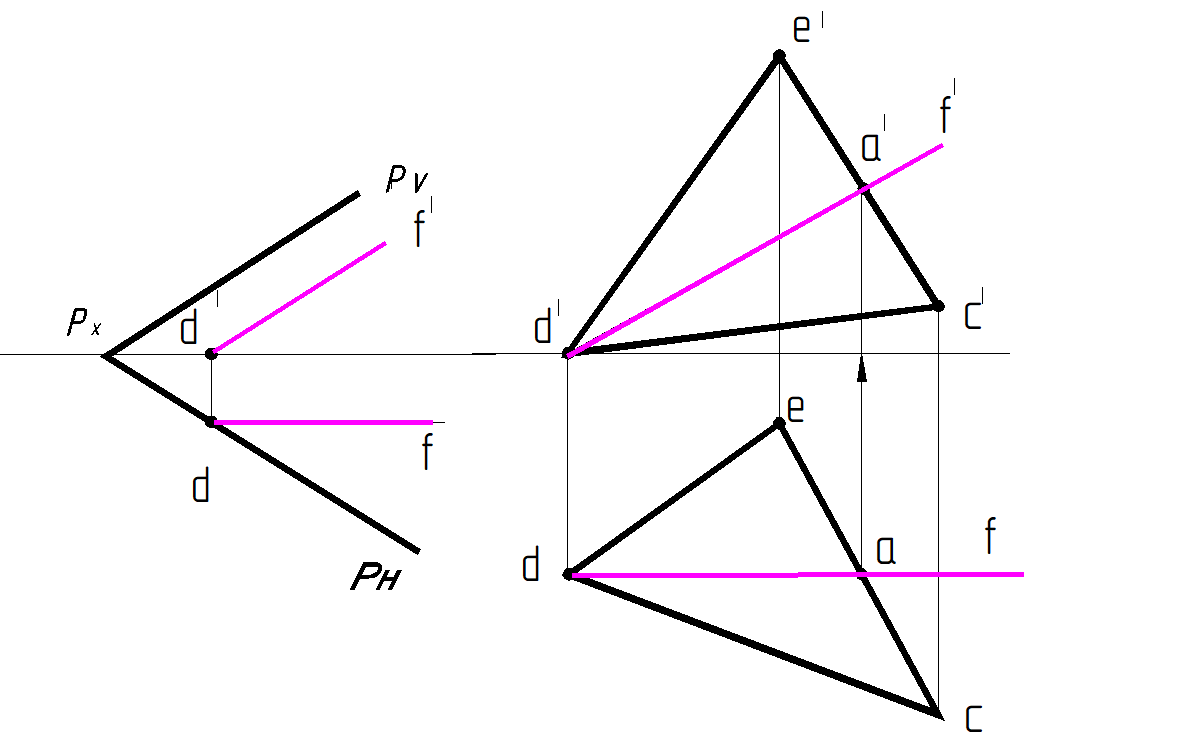
Рис. 61. Фронталь плоскости:

а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆С DE

 

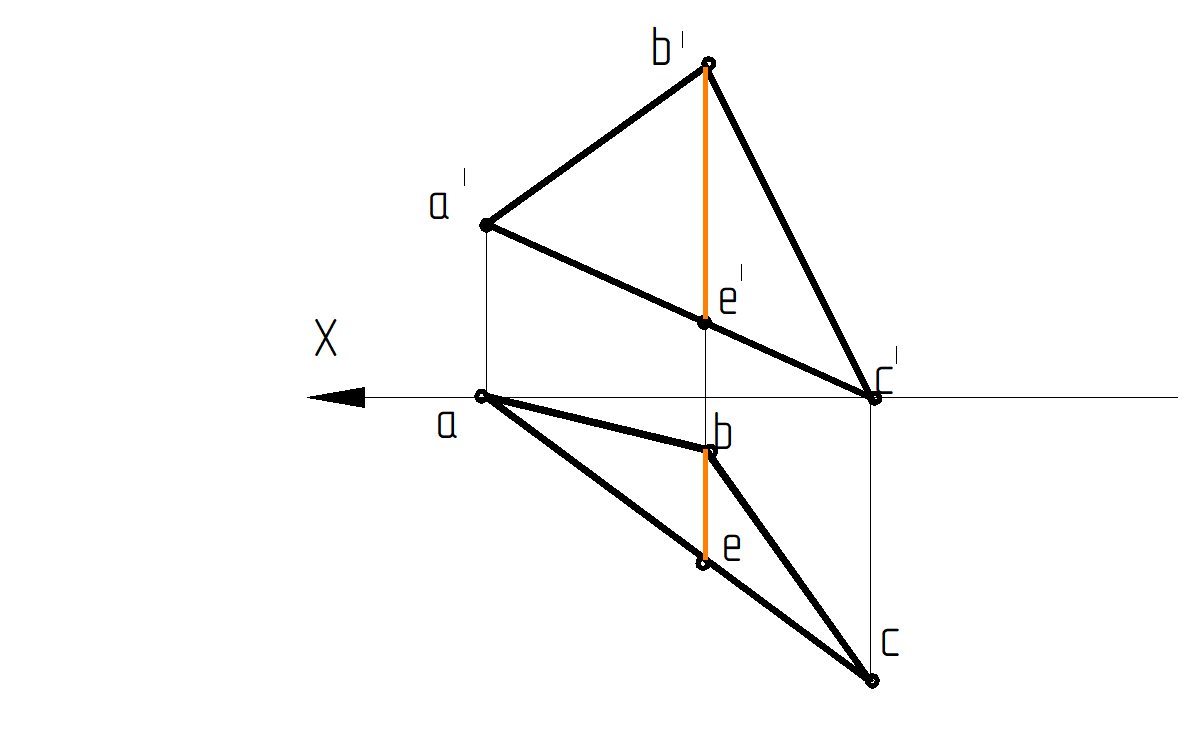
Рис. 62. Профильная прямая уровня ВЕ плоскости ∆АВС

Задача 1.

 Определить угол наклона плоскости Р(А DE ) к плоскости проекций Н. (рис. 66)

Решение:

1. В плоскости Р провести горизонталь Н ( h ', h).

2. Из вершины А, перпендикулярно горизонтали, построить отрезок АВ – линию ската, лежащую в этой плоскости; построение линии ската начинается с горизонтальной проекции при условии, что |ab| ⊥ h .

3. Определить действительную величину отрезка АВ методом прямоугольного треугольника, одним катетом которого будет горизонтальная проекция этого отрезка |ab|.

4. Искомым углом α является угол между гипотенузой |а_о b| треугольника (aba_o) и горизонтальной проекцией линии ската ab.

 

 

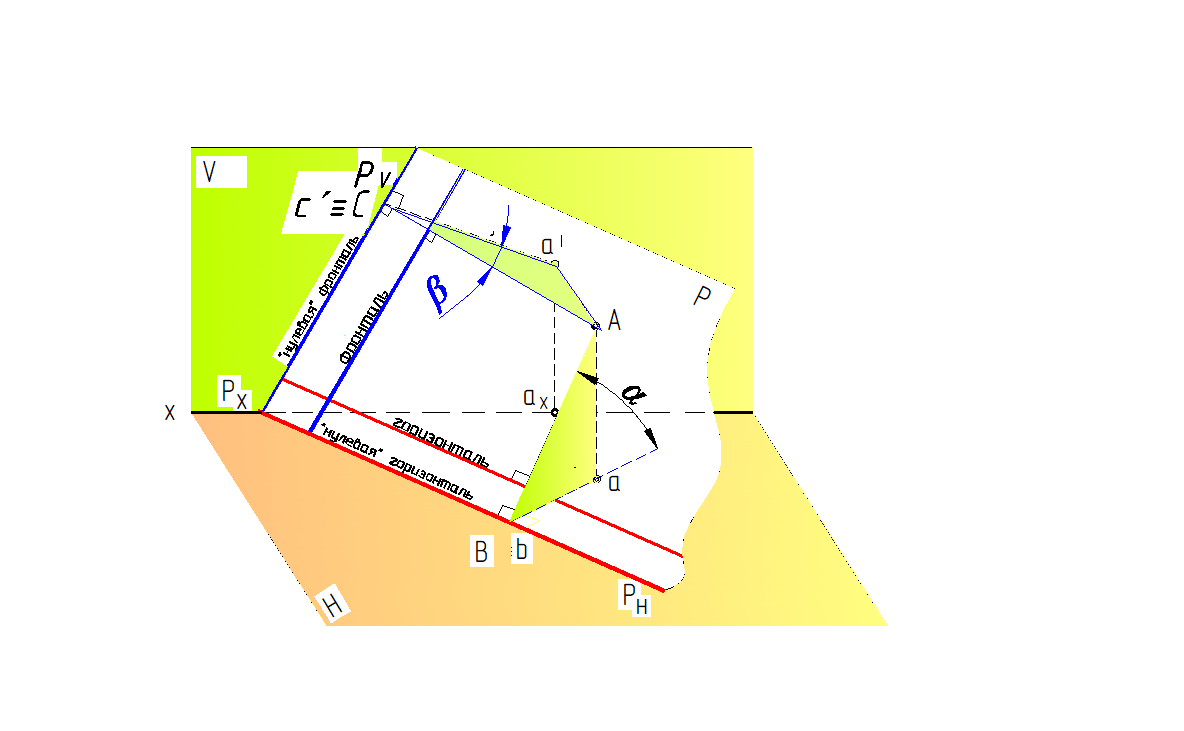
Рис. 65. Пространственная модель линий наибольшего наклона плоскости

 

 

 

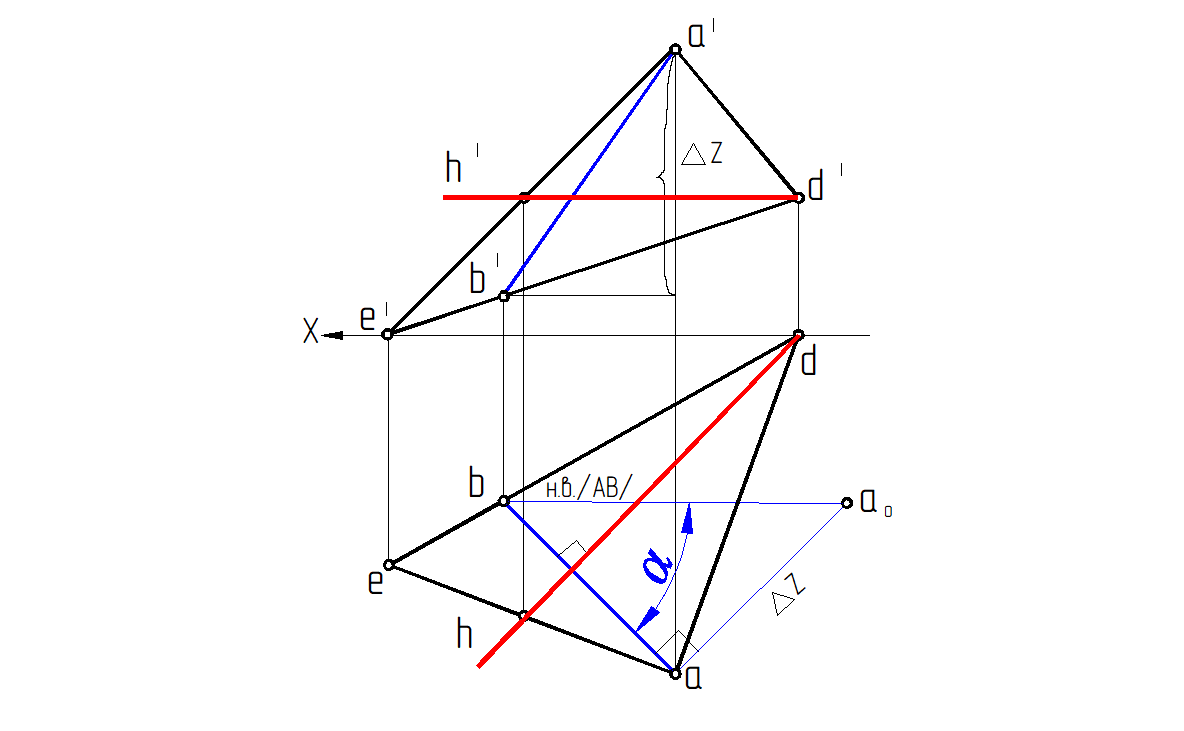
Рис. 66. Определение ∠α плоскости ∆АЕ D по линии ската

 

Задача 2.

 Определить угол наклона плоскости Р к плоскости проекций V . (рис. 67)

     Решение:

1. В плоскости Р провести фронталь F ( f ′, f ).

2. Из вершины А перпендикулярно фронтали, провести отрезок |АС| – линию наибольшего наклона, лежащую в этой плоскости, построение линии наибольшего наклона начинается с построения фронтальной проекции при условии, что a ′ c ′ ⊥ f ′.

3. Определить натуральную величину отрезка [АС] методом прямоугольного треугольника, одним катетом которого является его фронтальная проекция.

4. Искомым углом β является угол между гипотенузой а_ос′ треугольника a ′ c ′ a_o и фронтальной проекцией a ′ c′.

 

 

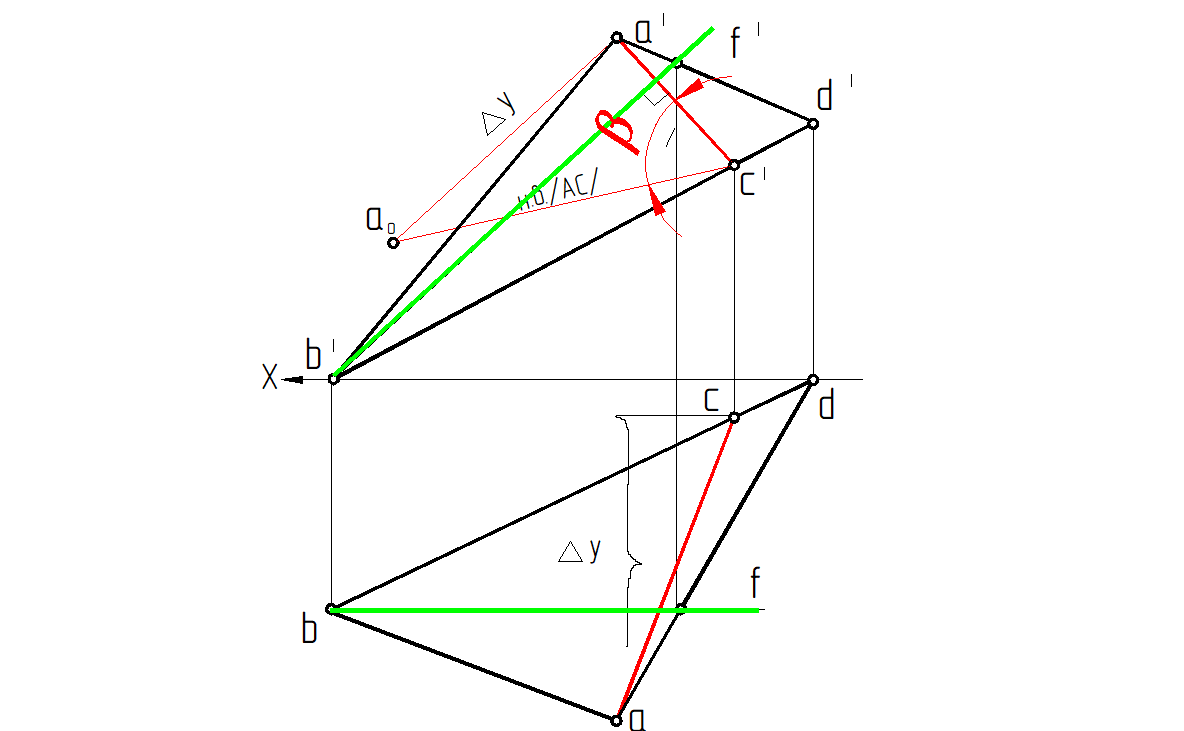
Рис. 67. Определение ∠β плоскости ∆ EAD по линии наибольшего наклона

 

4. Позиционные задачи

 

 

Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:

1. Задачи позиционные – решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов (в частном случае, выяснить их взаимную принадлежность) как по отношению друг к другу, так и относительно системы плоскостей проекций.

2. 3адачи метрические – при решении задач этой группы появляется возможность ответить на вопросы, касающиеся как внутренней метрики заданных геометрических объектов (определение расстояния между различными точками объекта и нахождение углов между линиями и поверхностями, принадлежащими этому объекту), так и определение расстояний между точками и величин углов между линиями и поверхностями, принадлежащими различным объектам.

3.Задачи комплексные – включают в себя элементы позиционных и метрических задач

 

Двух плоскостей

 

Прямая линия, не лежащая в плоскости, может иметь с ней только одну точку. Если эта точка собственная, то прямая и плоскость пересекаются, если несобственная, то – параллельны.

То же касается и взаимного положения двух плоскостей. Две плоскости пересекаются по прямой линии. Если эта прямая собственная, то плоскости пересекаются, если несобственная – параллельны, т. е. плоскости не имеют общих точек.

Рассмотрим сначала позиционные задачи на пересечение прямой и плоскости; двух плоскостей. Две из этих задач носят название вспомогательные, две другие – основные. Вспомогательными некоторые задачи называют потому, что по условию плоскость занимает в них частное положение.

Решив такие задачи, можно перейти к решению основных задач, где геометрические объекты занимают общее положение.

 

Вспомогательные (простейшие) позиционные задачи

Плоскостью

В этом случае построение линии пересечения упрощается тем, что одна ее проекция совпадает с проекцией проецирующей плоскости на ту плоскость проекций, к которой она перпендикулярна.

В качестве примера на рис. 69 показано построение проекций e ' d ', ed линии пересечения ED фронтально-проецирующей плоскости Р с плоскостью треугольника АВС:

ED = ( ABC ) ∩ P .

На фронтальной проекции в пересечении проекций а' b ' и а'с' со следом P_v находим фронтальные проекции e ' и d ' двух общих точек заданных плоскостей:

 

а' b ' ∩ P_v = e '; а'с' ∩ P_v = d '.

По ним построены горизонтальные проекции e и d на горизонтальных проекциях ab и ас сторон треугольника. Через точки e и d проводим горизонтальную проекцию линии пересечения плоскостей.

При взгляде по стрелке S по фронтальной проекции очевидно, что часть треугольника левее линии пересечения Е D ( e ' d ') находится над плоскостью Р, т. е. видима, остальная часть – под плоскостью Р, т. е. невидима (участок ade показан штриховой линией).

 

 

 

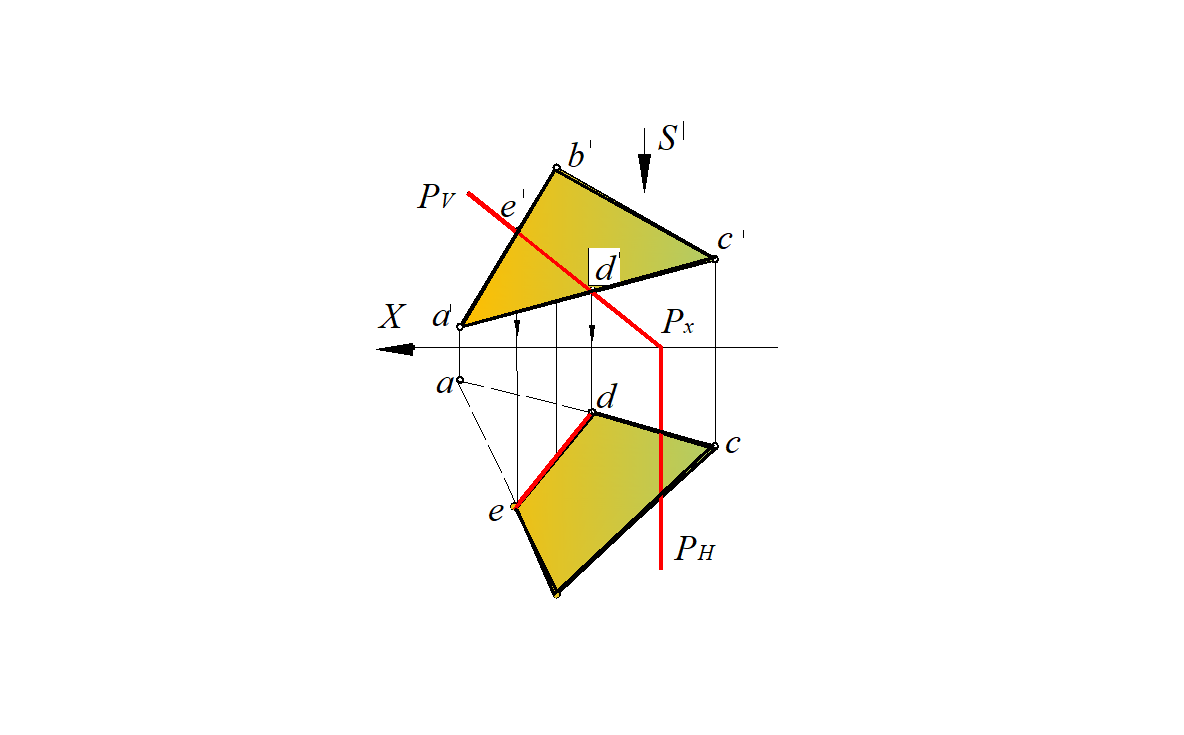
Рис. 69. Построение линии пересечения плоскости общего положения АВС

с проецирующей плоскостью Р, заданной следами

S–направление взгляда при определении видимости объектов

 

Другой пример построения линии пересечения двух тре­угольников (ABC) и (DEF), один из которых (DEF) задан как горизонтально-проецирующая плоскость, приведен на рис.3.MN = ( ABC ) ∩ ( DEF ).

 

На горизонтальной проекции в пересечении гори­зонтальных проекций ab и be сторон ∆АВС с проекцией ( dfe ) вто­рого треугольника находим горизонтальные проекции m и n точек их пересечения:

 

ab ∩ (dfe) = m; be ∩ (dfe) = n.

 

По ним на фронтальных проекциях сторон а' b ' и b 'с' строим фронтальные проекции т' и п' точек линии пересечения MN .

На фронтальной проекции отмечаем видимость частей треугольников, руководствуясь следующим: при взгляде по стрелке S по горизонтальной проекции очевидно, что сторона АС находится перед плоскостью треугольника (DEF).

Следовательно, сторона АС и ограничиваемая ею часть треугольника (A ВС) до линии пересечения MN видимы (т. е. видима фронтальная проекция четырехугольника а'с'п'т'). Видимая часть фронтальной проекции ∆DEF на чертеже оттенена.

 

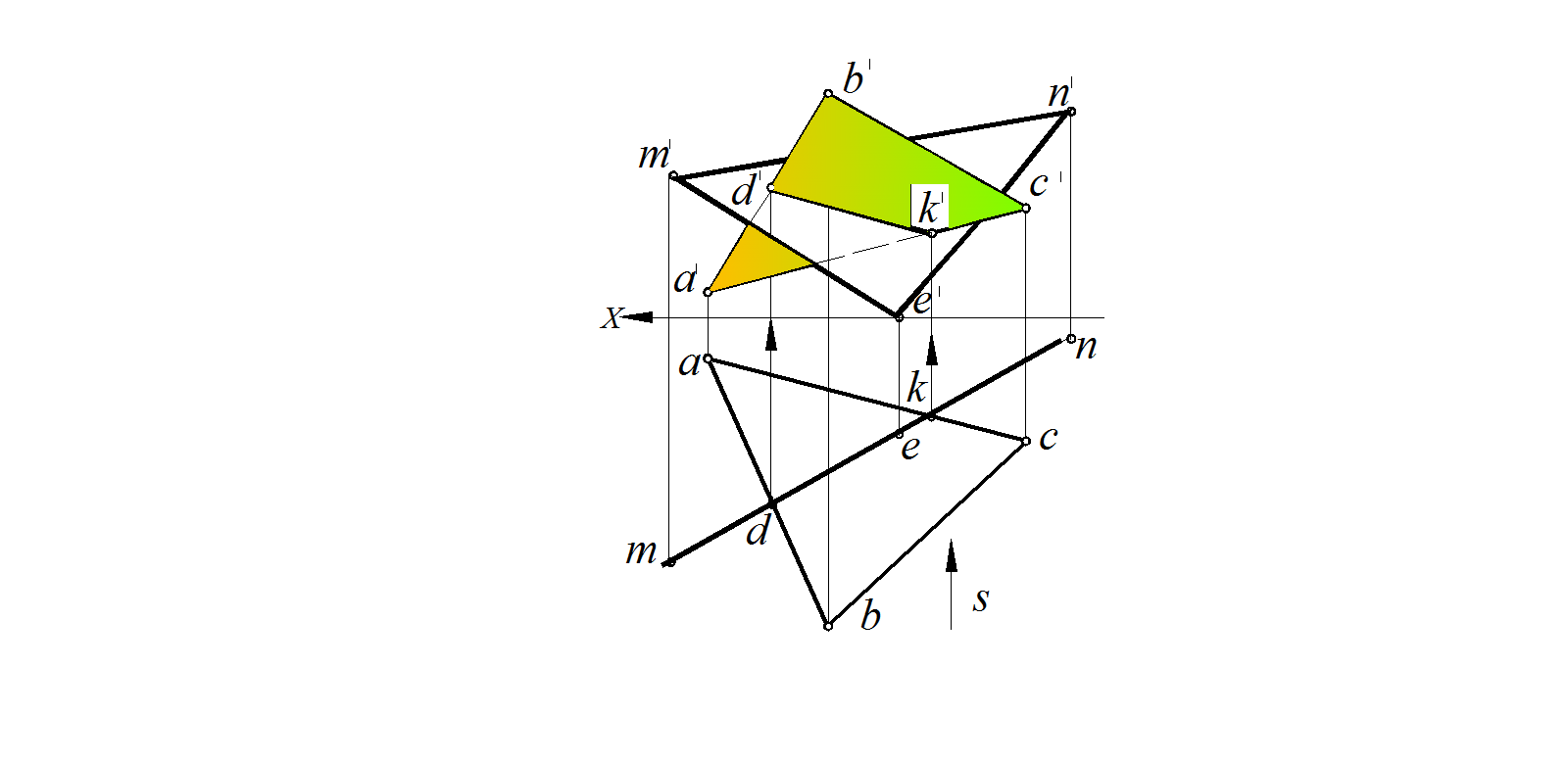
Рис. 70. Построение линии пересечения плоскости общего положения ∆АВС

с проецирующей плоскостью, заданной ∆MNE

S–направление взгляда при определении видимости объектов

 

Основные позиционные задачи

 

Задача.

Построить линию пересечения ЕК плоскости ∆АВС с плоскостью ∆ NDM (рис. 74):

Решение:

Строим линию пересечения (ABC) ∩ ( NDM ) = EK

1. E = DN ∩ ∆ ABC

DN 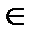T T_┴ V; T ∩ ∆ ABC =3–4; 3–4∩ dn= e; E 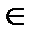DN ; e '  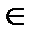 d ' n ' . (рис. 75)

2.  K = BC ∩ ( NDM )

BC 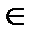 P; P ⊥V; P ∩ ∆ NDM = 1-2  1-2∩ bc= k; K 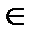BC ; k ' 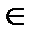b ' c ' . (рис. 76)

3. Соединяем точки Ки Е - получаем линию пересечения заданных плоскостей (рис. 77)

 

4. Определяем взаимную видимость плоскостей по конкурирующим точка (рис.78)

 

 

 

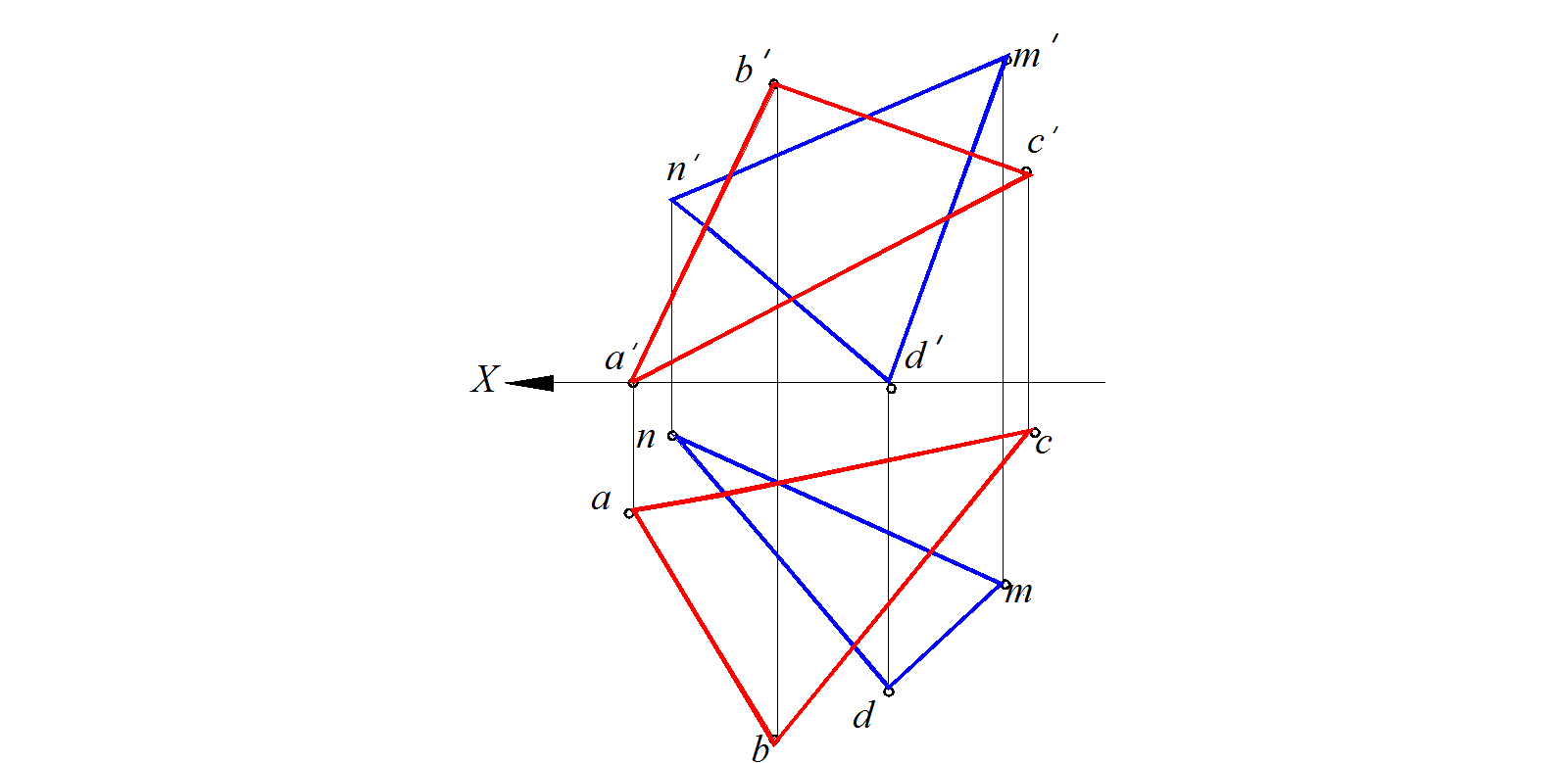
Рис. 74.Условие к задачи - построение линии пересечения двух плоскостей общего положения

 

 

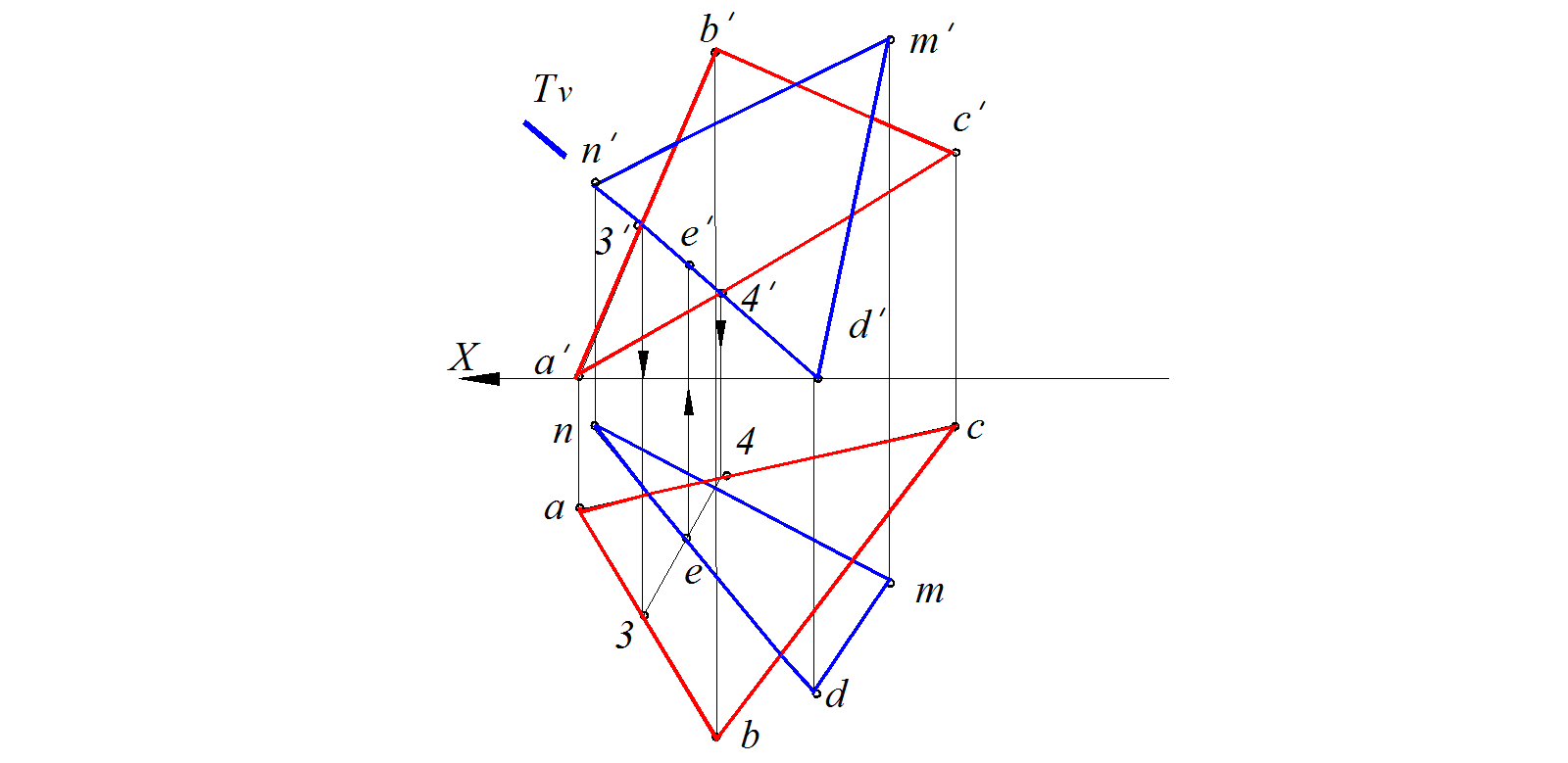
Рис.75. Построение линии пересечения двух плоскостей общего положения. Построение точки Е

 

 

 

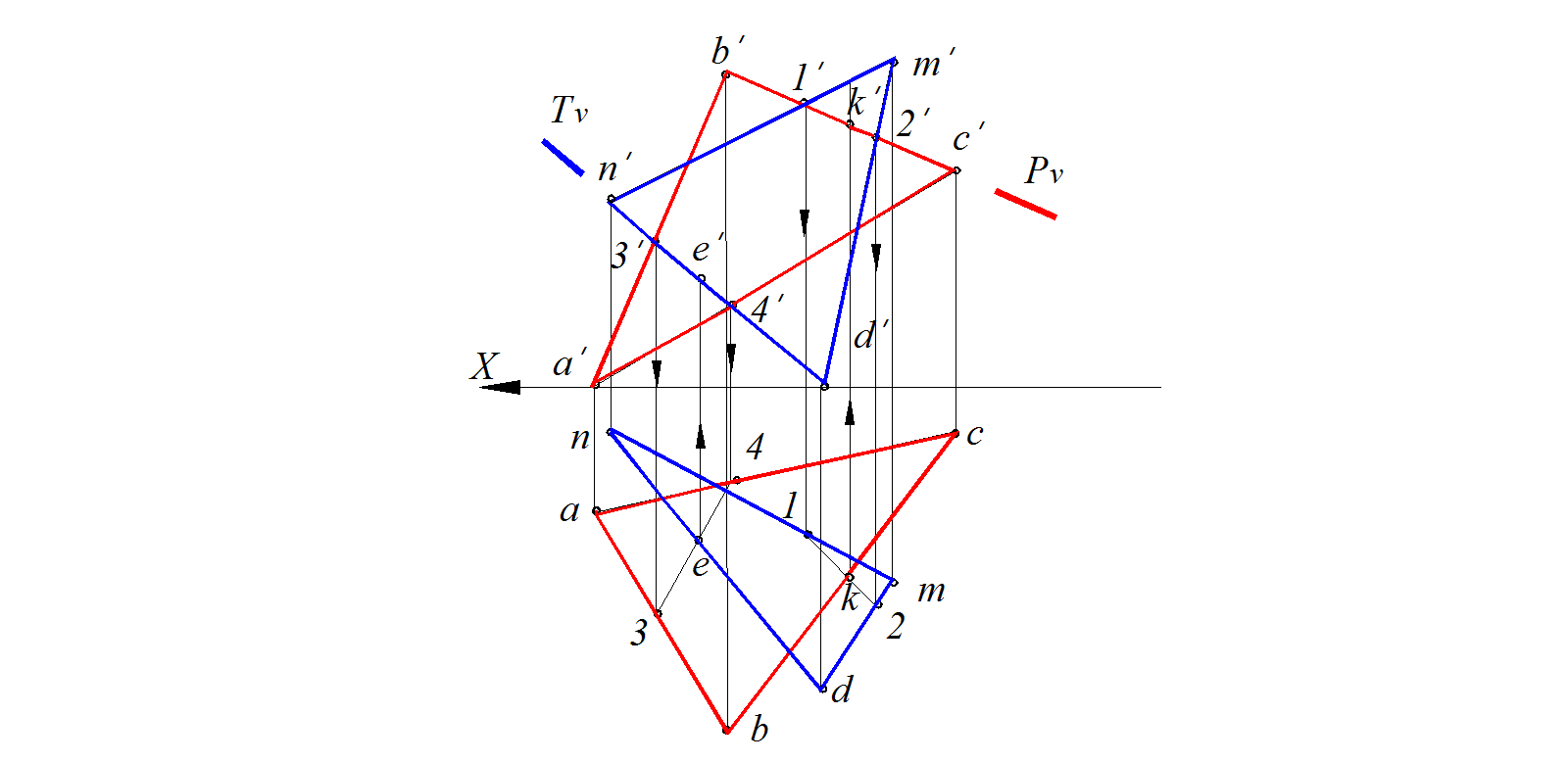
Рис. 76. Построение линии пересечения двух плоскостей общего положения. Построение точки К

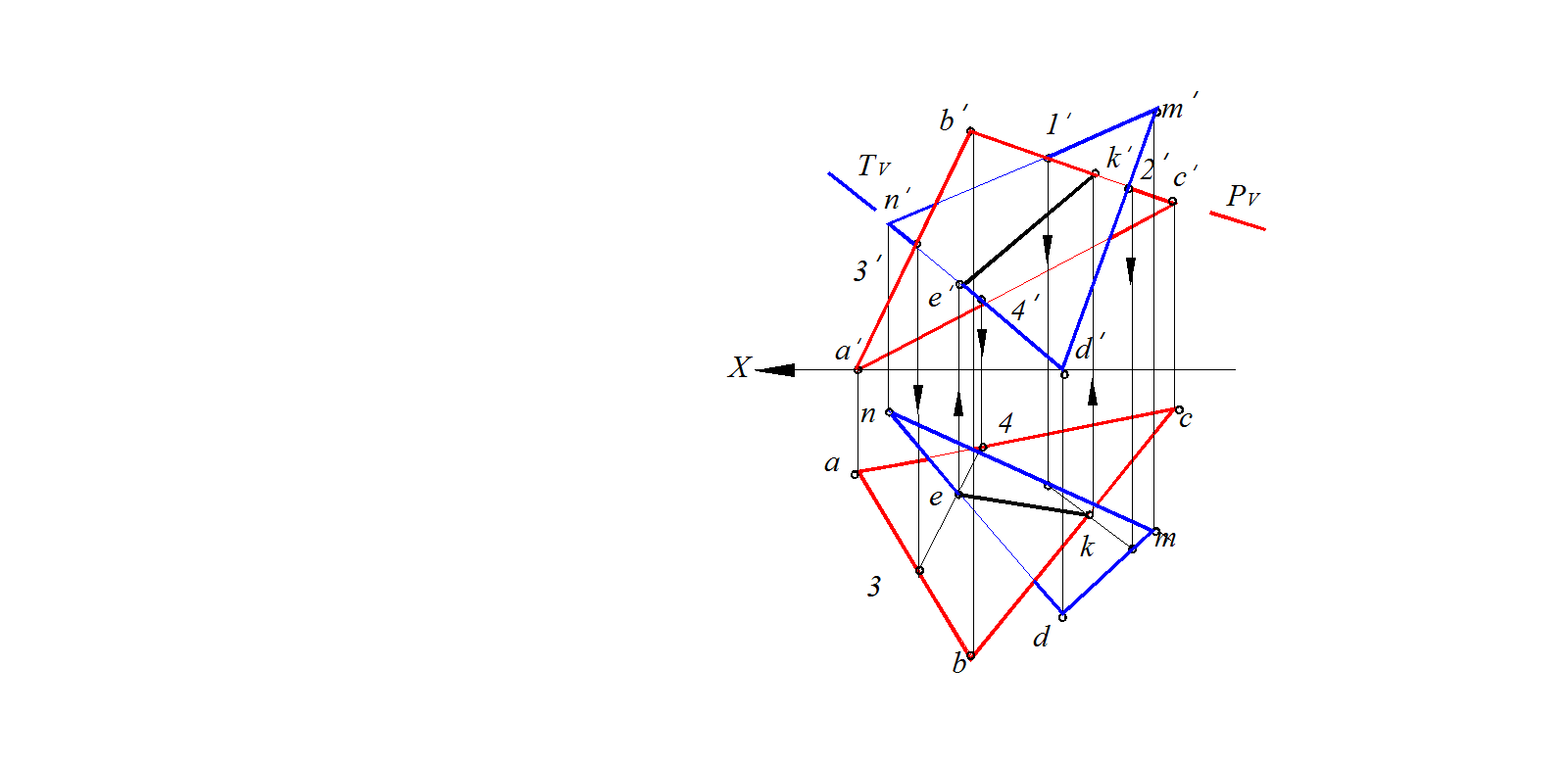
Рис.77. Построение линии пересечения двух плоскостей общего положения –ЕК

 

 

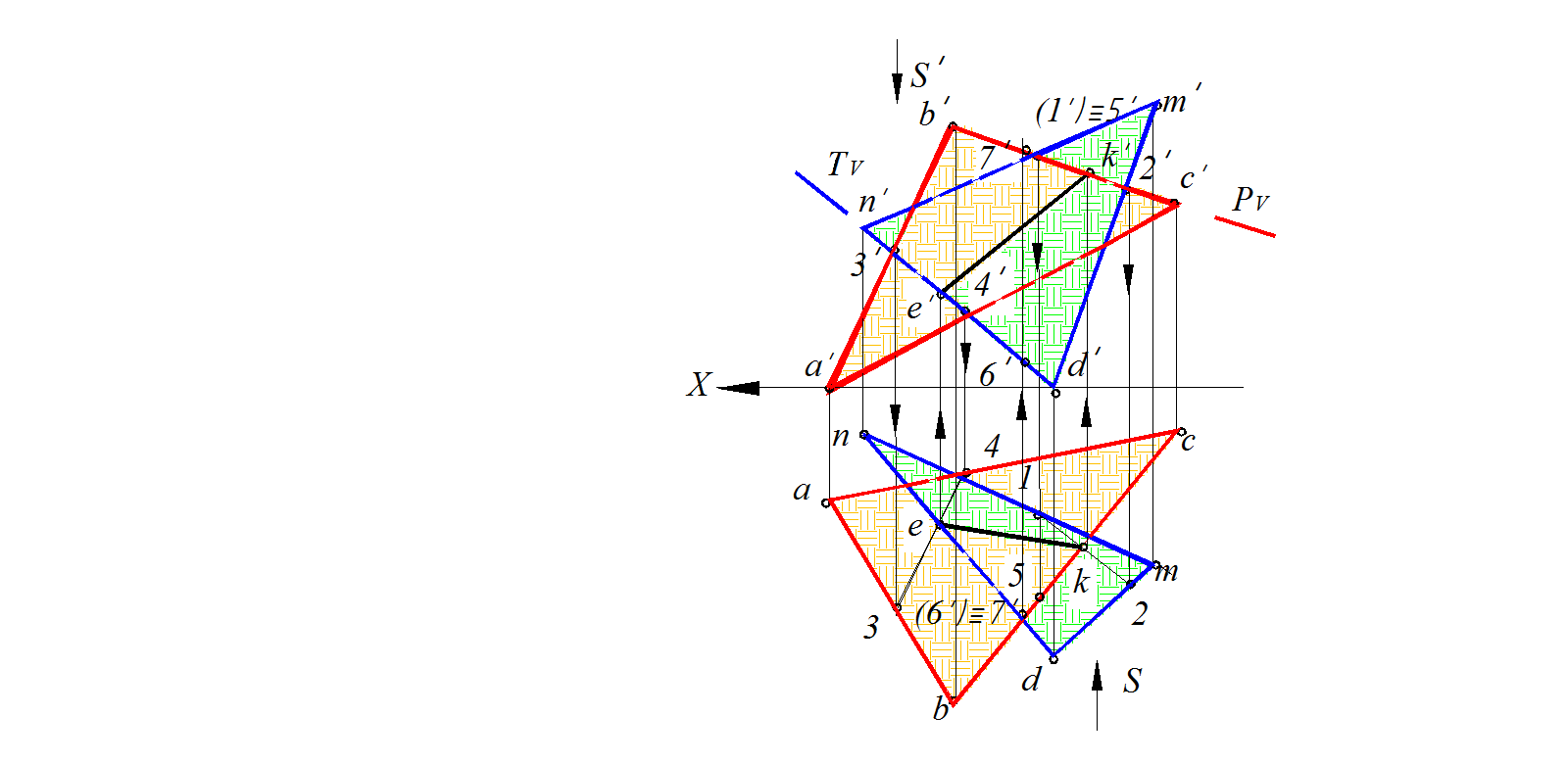
Рис. 78. Построение линии пересечения двух плоскостей общего положения.

Определение взаимной видимости плоскостей

Задача.

Задача.

Из точки C восстановить перпендикуляр – прямую М к плоскости ∆ ABC. (рис. 81,а)

Прямая, перпендикулярная плоскости, перпендикулярна любой прямой этой плоскости. Следовательно, по теореме, она перпендикулярна горизонтали и фронтали этой же плоскости.

Решение:

1. Проведем в заданной плоскости общего положения ∆АВС горизонталь CD (рис. 81, б).

2. Согласно теореме проведенная прямая должна соответствовать условию: М⊥С D , На чертеже прямая М проводится: m⊥cd ; (рис. 82, а).

  3. Проведем в заданной плоскости общего положения ∆АВС фронталь АЕ (рис. 82, б).

4. Согласно теореме проведенная прямая должна соответствовать M⊥АЕ . На чертеже прямая М проводится: m ' ⊥a ' e '.

5. Следовательно, из точки с проводим прямую на горизонтальной проекции m⊥cd   и на фронтальной проекции из точки с′– прямую m ' ⊥a ' e ' (рис. 83).

 

                                          а                                                    б

 

 

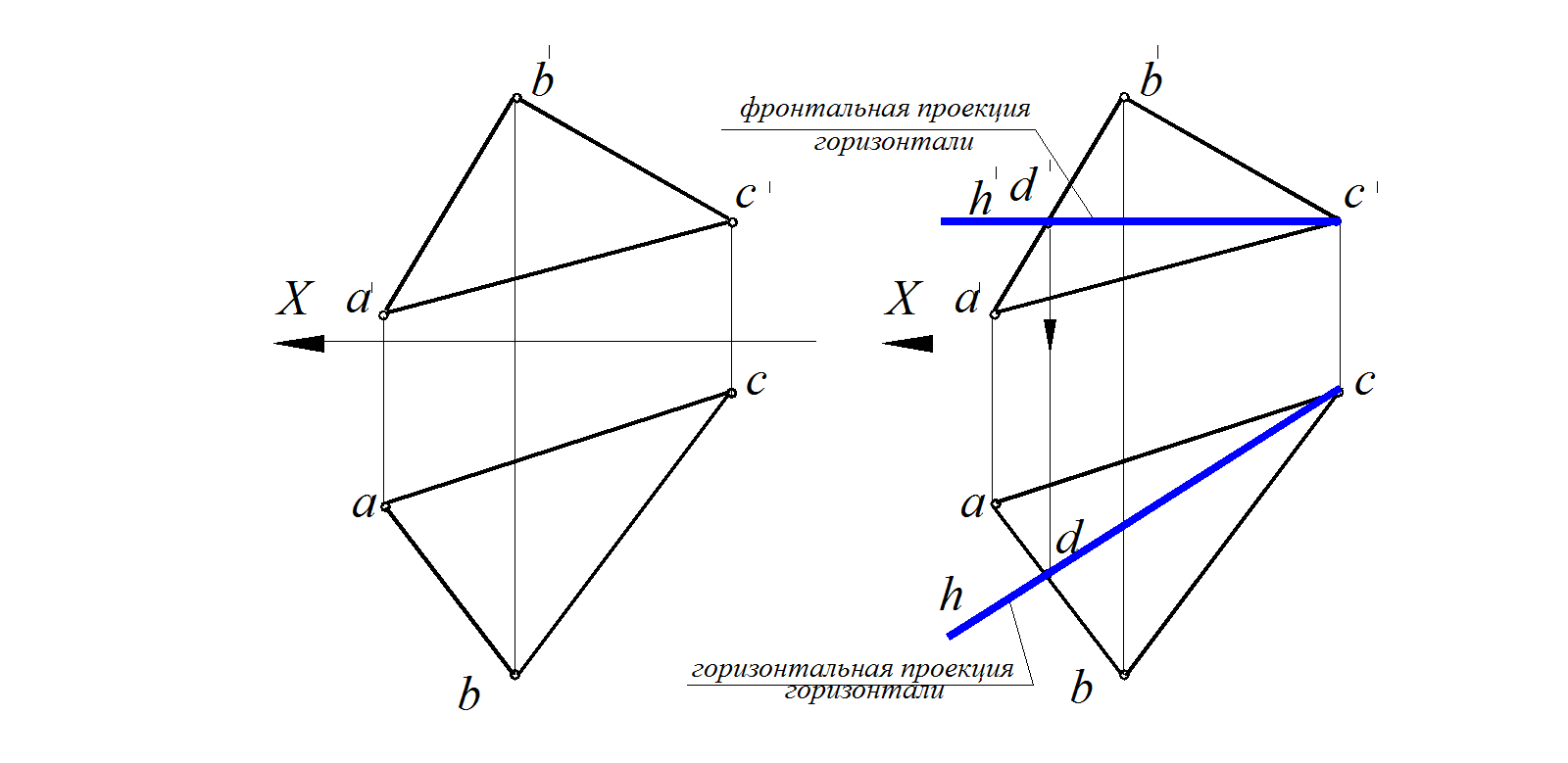
Рис. 81. Построение перпендикуляра к плоскости общего положения:

   а – условие задачи               б– построение горизонтали в плоскости ∆АВС

 

 

                а                                                                                                  б                                 

 

 

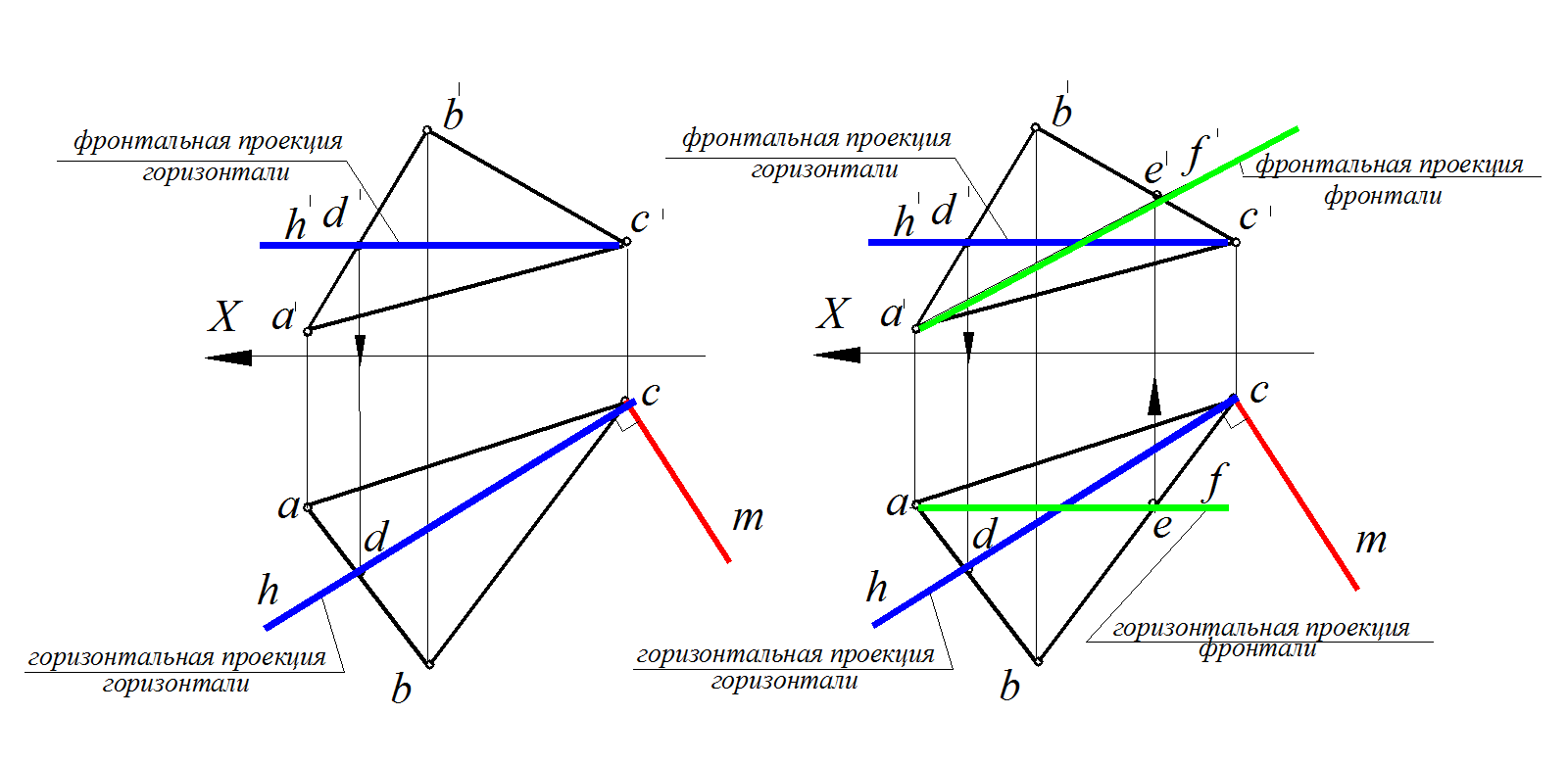
Рис.82. Построение перпендикуляра к плоскости общего положения:

 а –построение горизонтальной проекции перпендикуляра  

 б– построение фронтали в плоскости ∆АВС

 

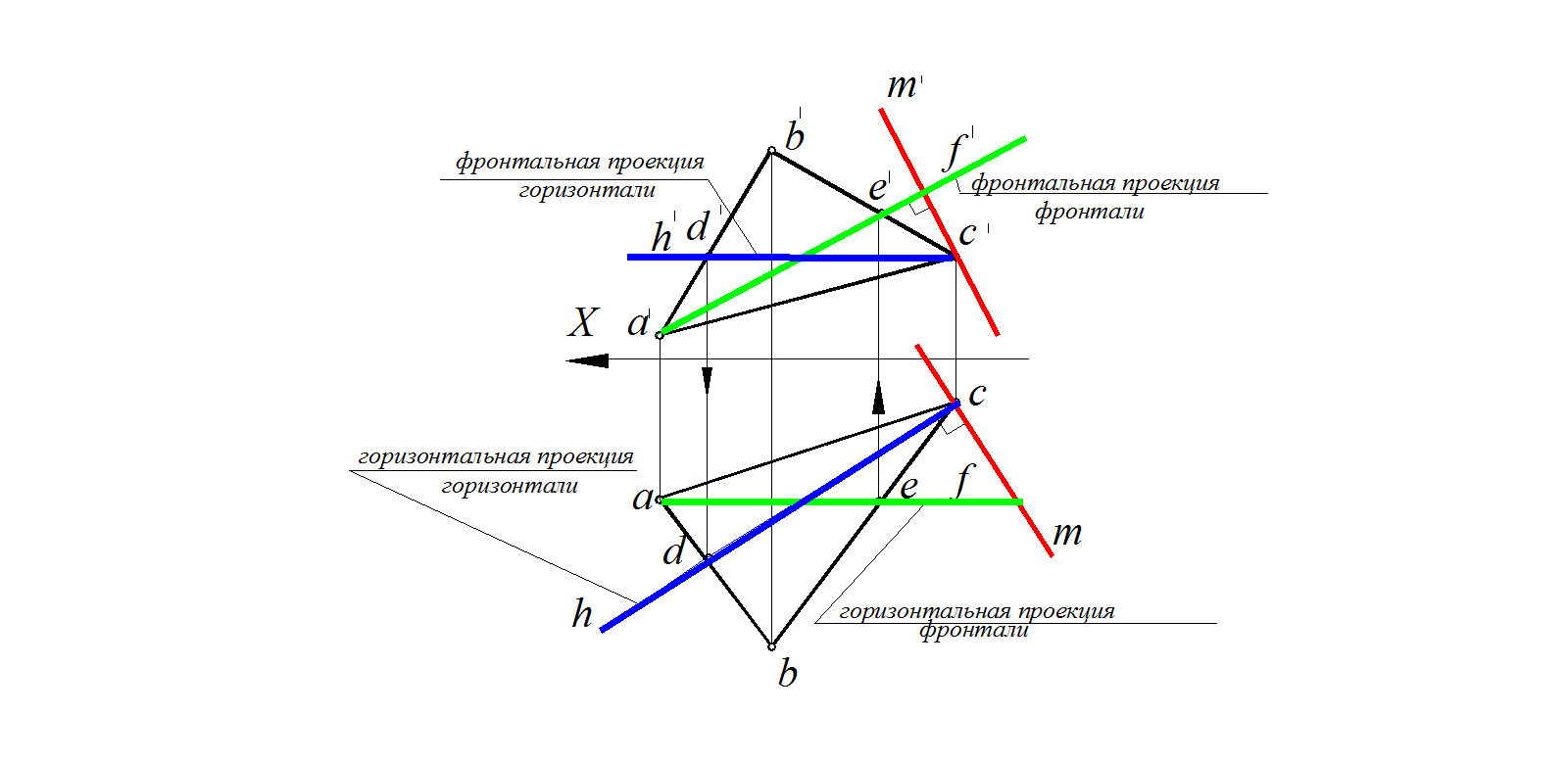
Рис. 83. Построение перпендикуляра к плоскости общего положения

 

Если плоскость задана следами (рис. 84), мы получаем следующий вывод: если прямая перпендикулярна к плоскости, то ее горизонтальная проекция перпендикулярна горизонтальному следу плоскости (нулевой горизонтали), фронтальная проекция перпендикулярна фронтальному следу плоскости (нулевой фронтали). На рис. 84 через точку В проведена прямая, перпендикулярная плоскости Р, заданной на чертеже следами.

 

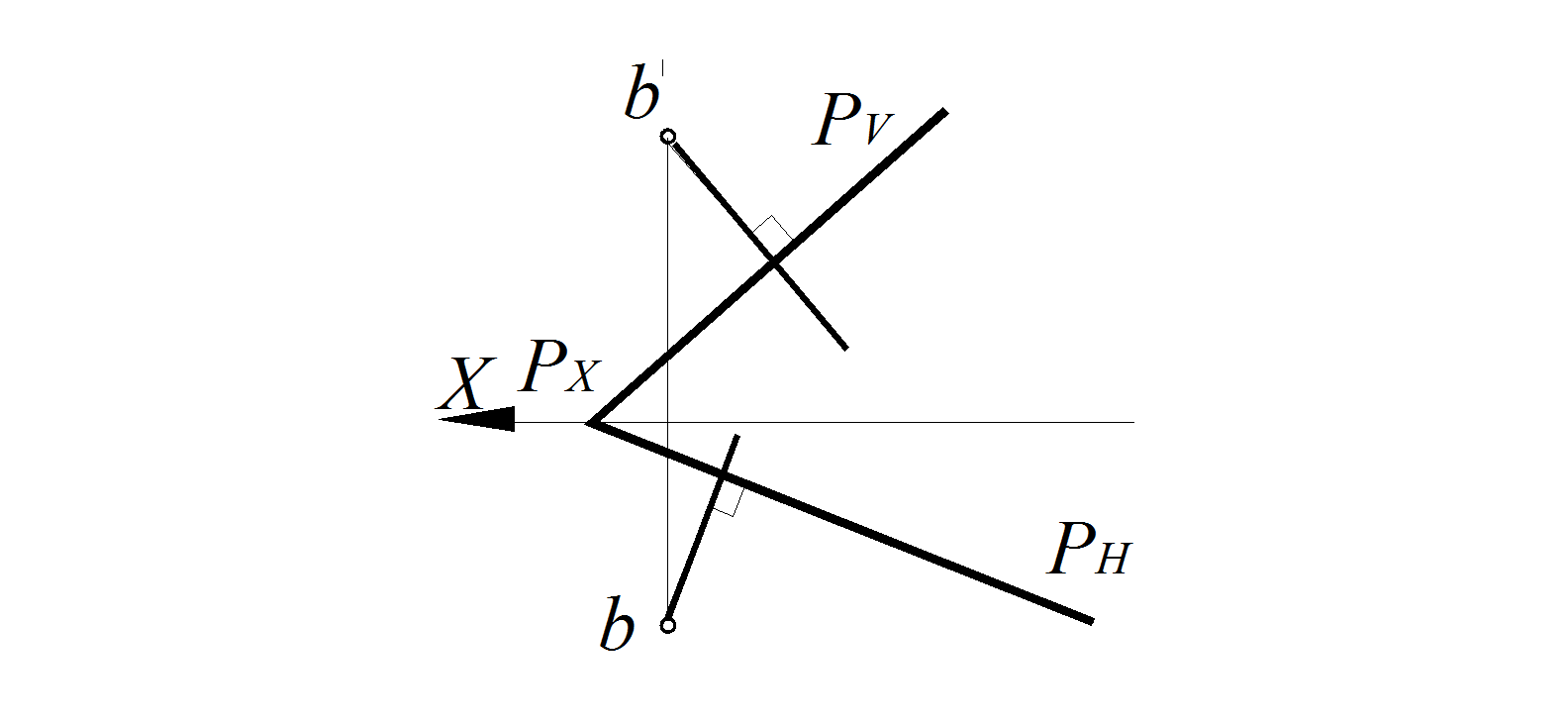
Рис. 84. Прямая, перпендикулярная плоскости Р, заданной следами

Применяя эту теорему можно легко решить обратную задачу – построить плоскость, перпендикулярную заданной прямой (рис. 85).

 

Задача.

Задача.

Через данную прямую MN провести плоскость перпендикулярную данной плоскости ∆АВС. Дополнительным условием здесь служит то, что искомая плоскость должна проходить через прямую MN.

Решение:

1. Анализируем условие задачи: прямая MN общего положения и плоскость общего положения, заданная ∆АВС (рис. 87), стороны ∆АВС являются горизонталью АС и фронталью АВ.

  2. Прямую MN заключаем в плоскость Р ( MN ∩ NE ). NE ⊥ ( ABC ); en⊥ac ; e ' n '⊥a ' b ' .

  Построение здесь облегчено тем, что стороны ∆АВС являются горизонталью АС и фронталью АВ. В ином случае их предварительно необходимо построить.                                                           

 

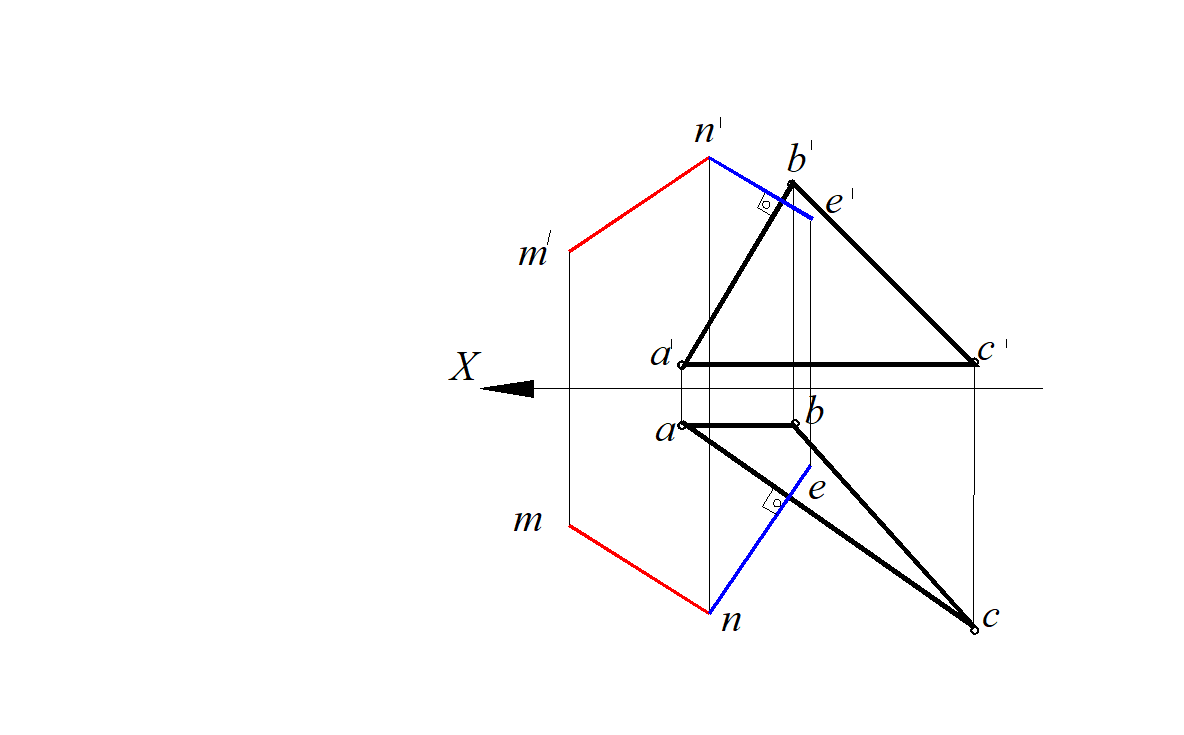
Рис. 87. Построение взаимно перпендикулярных плоскостей:

 

Задача.

Построить плоскость Р, перпендикулярную фронтальной плоскости проекций и плоскости, заданной ∆АВС (рис.88)

Решение:

1. Строим в плоскости ∆АВС фронталь С1. Дополнительным условием здесь является то, что искомая плоскость должна быть еще перпендикулярна плоскости проекций V .

2. Проводим плоскость Р, заданную следами, перпендикулярно фронтали треугольника. Р ⊥V ; Р _v⊥c 1; Р ⊥ (АВС).

 

 

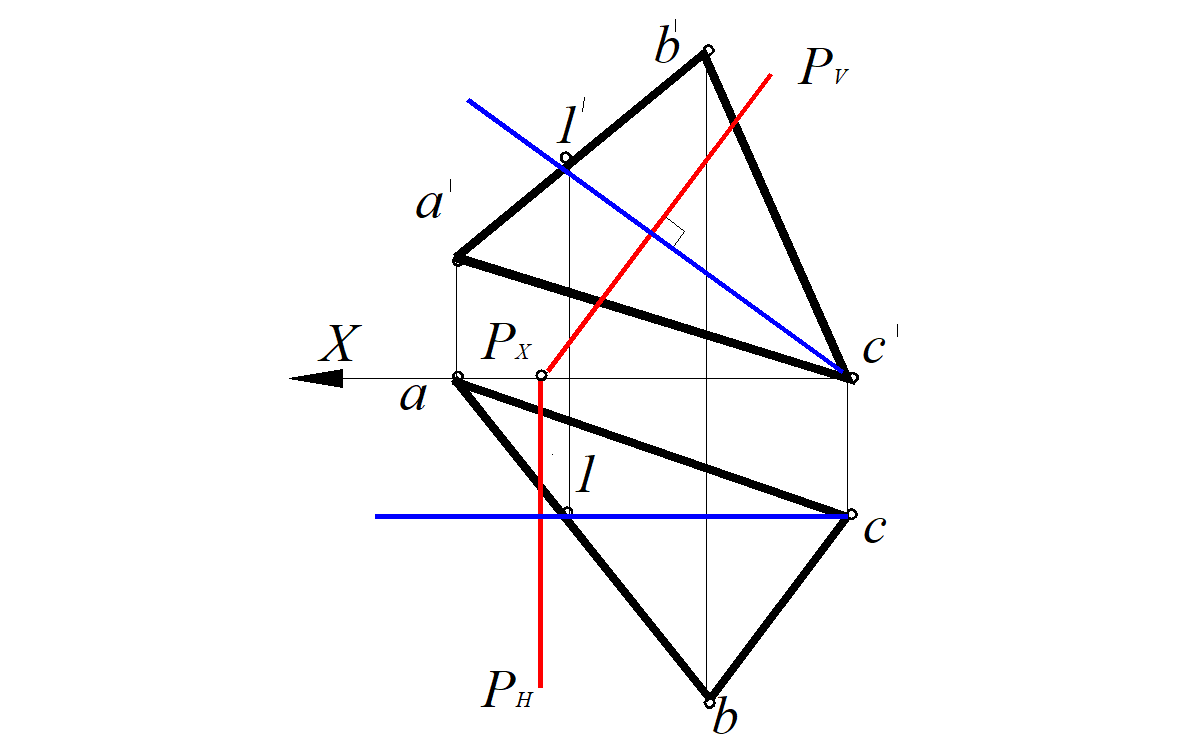
Рис. 88. Построение плоскости перпендикулярной

заданной плоскости ∆АВС и плоскости проекций V

 

Параллельных между собой

При построении используем известный из стереометрии признак: если прямая, не принадлежащая плоскости, параллельна какой-либо прямой в этой плоскости, то она параллельна и самой плоскости.

Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие.

 

Задача 1. Через точку D (рис. 89, а) требуется провести прямую, параллельную плоскости, заданной треугольником ( ABC ), и плоскости проекций H (дополнительное условие).

Решение:

   Очевидно, искомая прямая должна быть параллельна линии пересечения обеих плоскостей, т. е. должна быть параллельна горизонтальному следу плоскости. Горизонтальный след плоскости –это нулевая горизонталь. Горизонтали одной и той же плоскости параллельны между собой.  Для определения направления этого следа можно воспользоваться горизонталью плоскости A ВС А1(h и h ′) , где через точку D проведена прямая, параллельная этой горизонтали.

 

а                                                                                      б

 

 

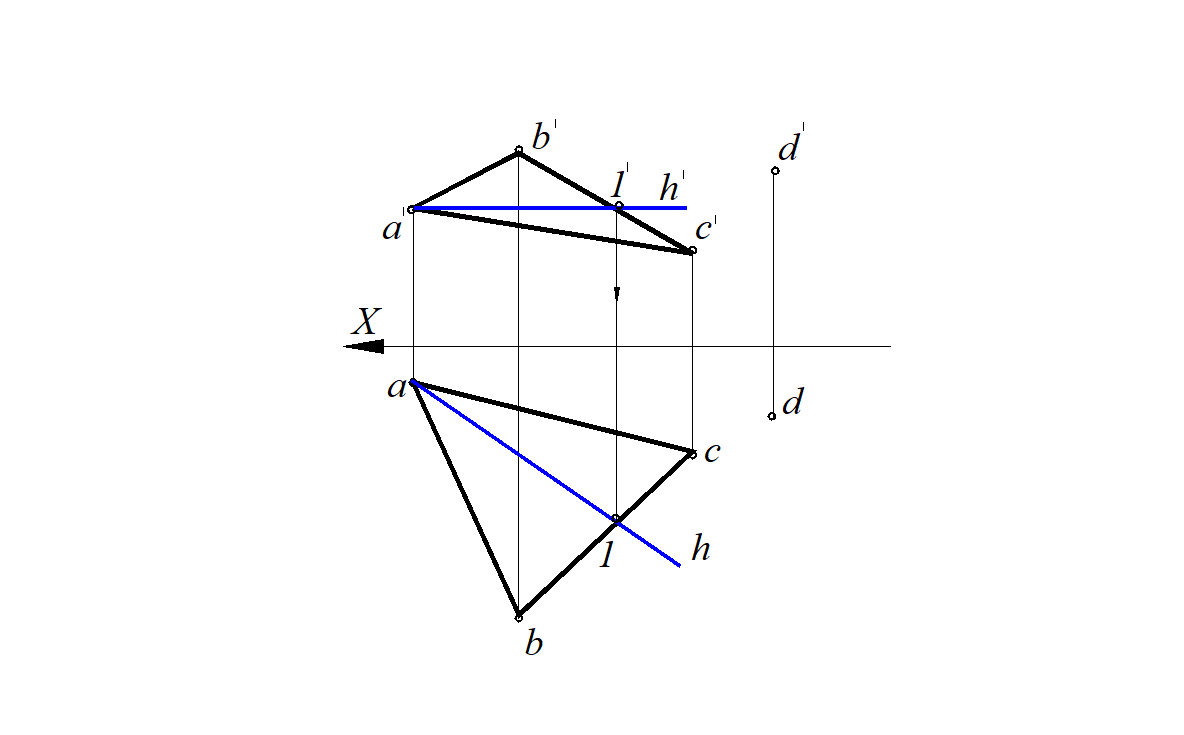
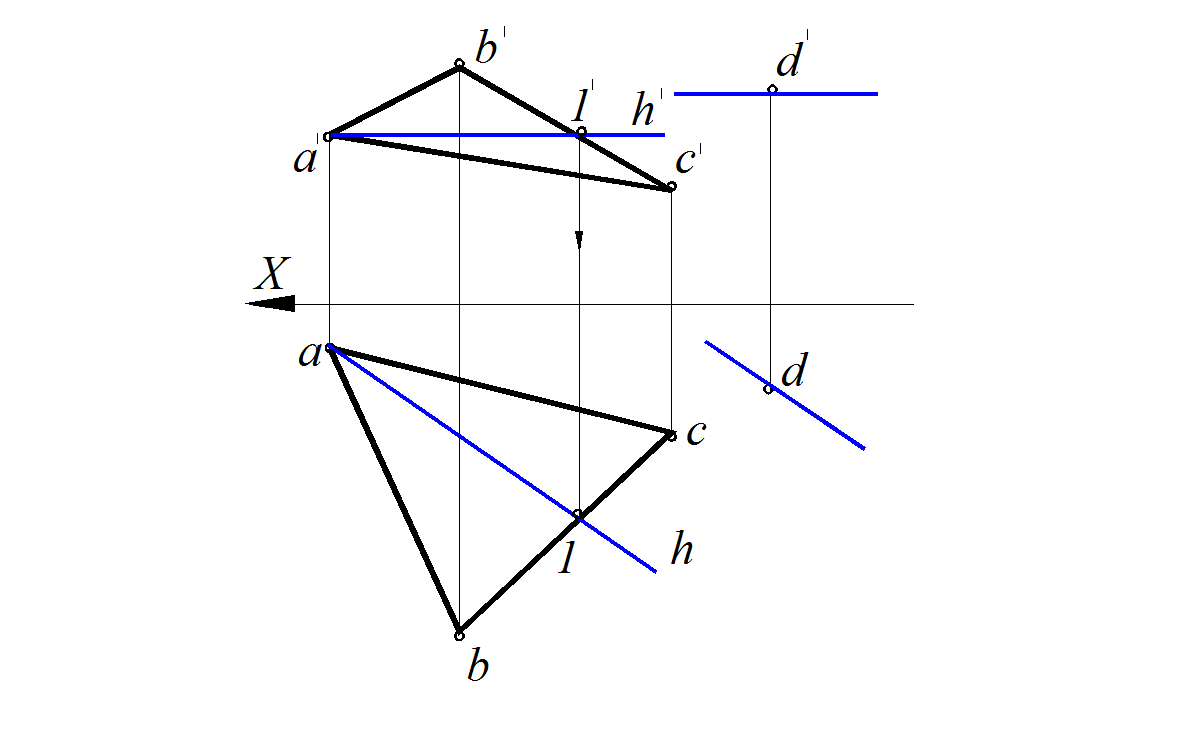
             Рис. 89. Построение взаимно параллельных прямой и плоскости

а – проведение прямой параллельной плоскости Н; б – плоскости параллельной прямой

 

 

Задача 2.

Через прямую СВ провести плоскость, параллельную прямой А D (рис. 90)

 

 

 

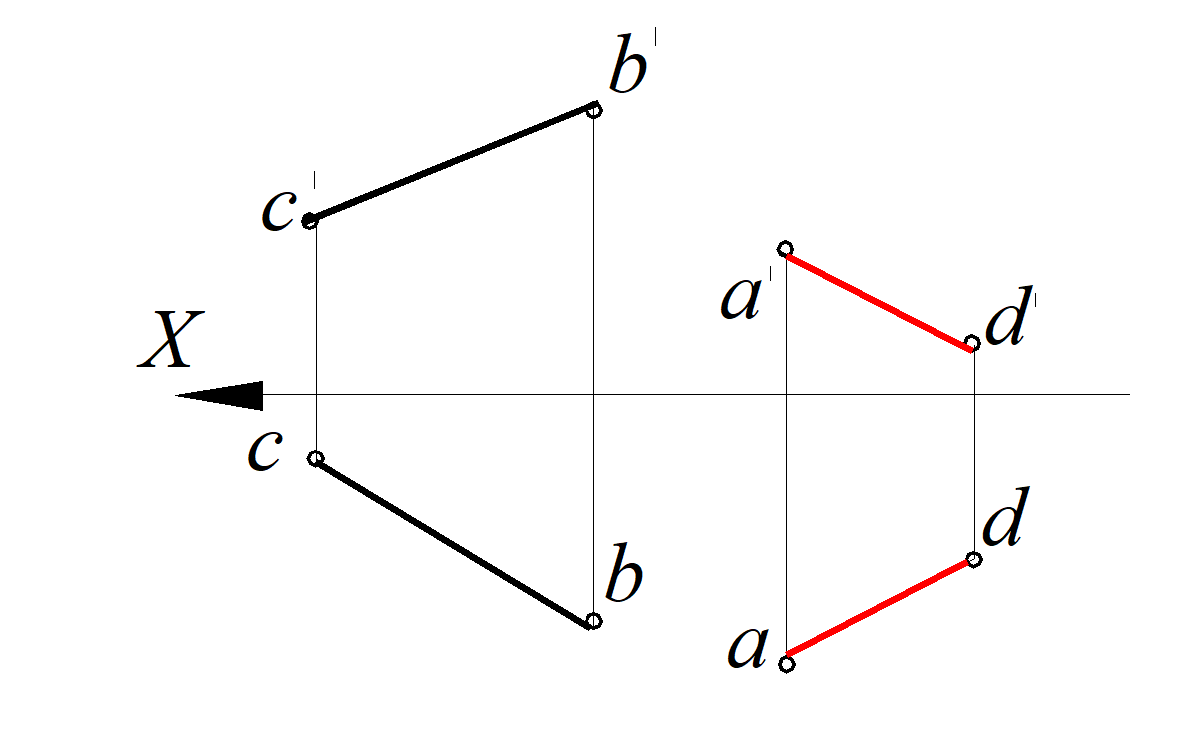
Рис. 90. Условие задачи

 

 

 

.                                                                                   

 

 

 

               

 

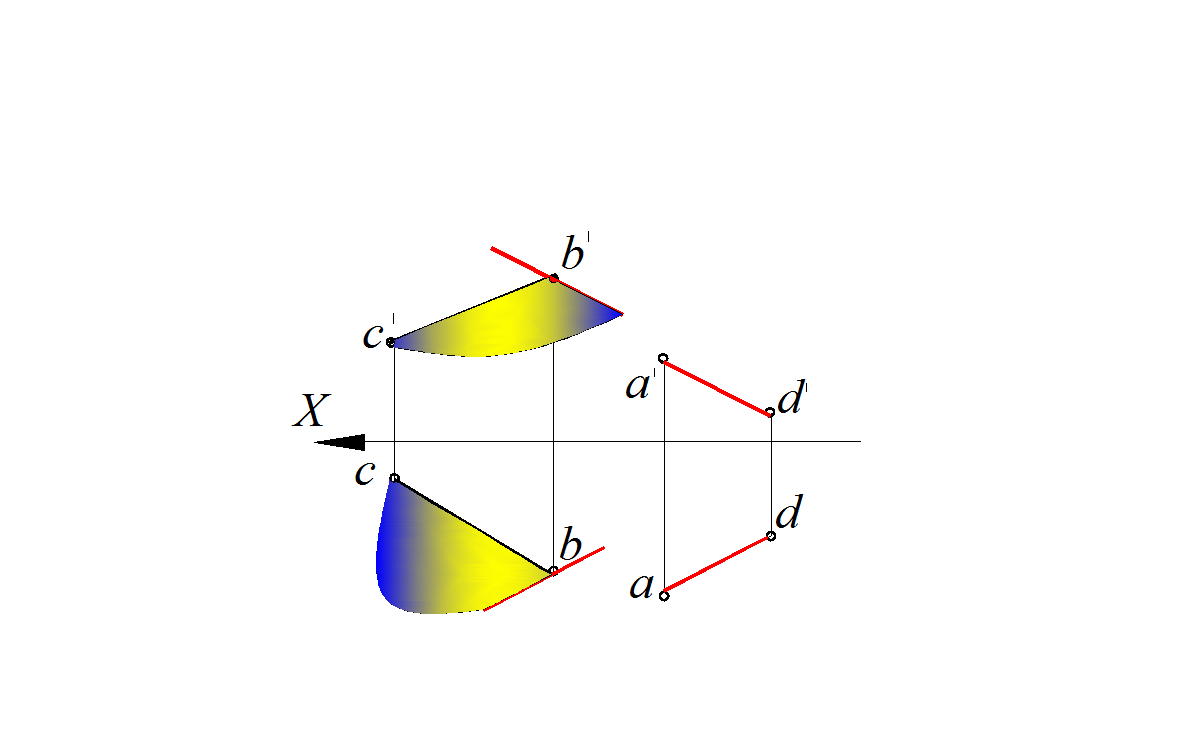
Рис. 91. Построение взаимно параллельных прямой и плоскости

плоскости параллельной прямой

 

 

Решение:

 

Прямые СВ и А D – скрещивающиеся. Если через одну из двух скрещивающихся прямых требуется провести плоскость, параллельную другой, то задача имеет единственное решение. Через точку В проведена прямая, параллельная прямой С D; пересекающиеся прямые АВ и BE определяют плоскость, параллельную прямой CD (рис. 91).

 

Задача.

Через точку D провести плоскость, параллельную плоскости, заданной пересекающимися прямыми A В и АС (рис. 92).

Решение:

Через точку D проводим прямые DE и DN , соответственно параллельные прямым AB и AC , следовательно, плоскость, заданная прямыми DK и Е K , окажется параллельной заданной плоскости. (рис. 93)

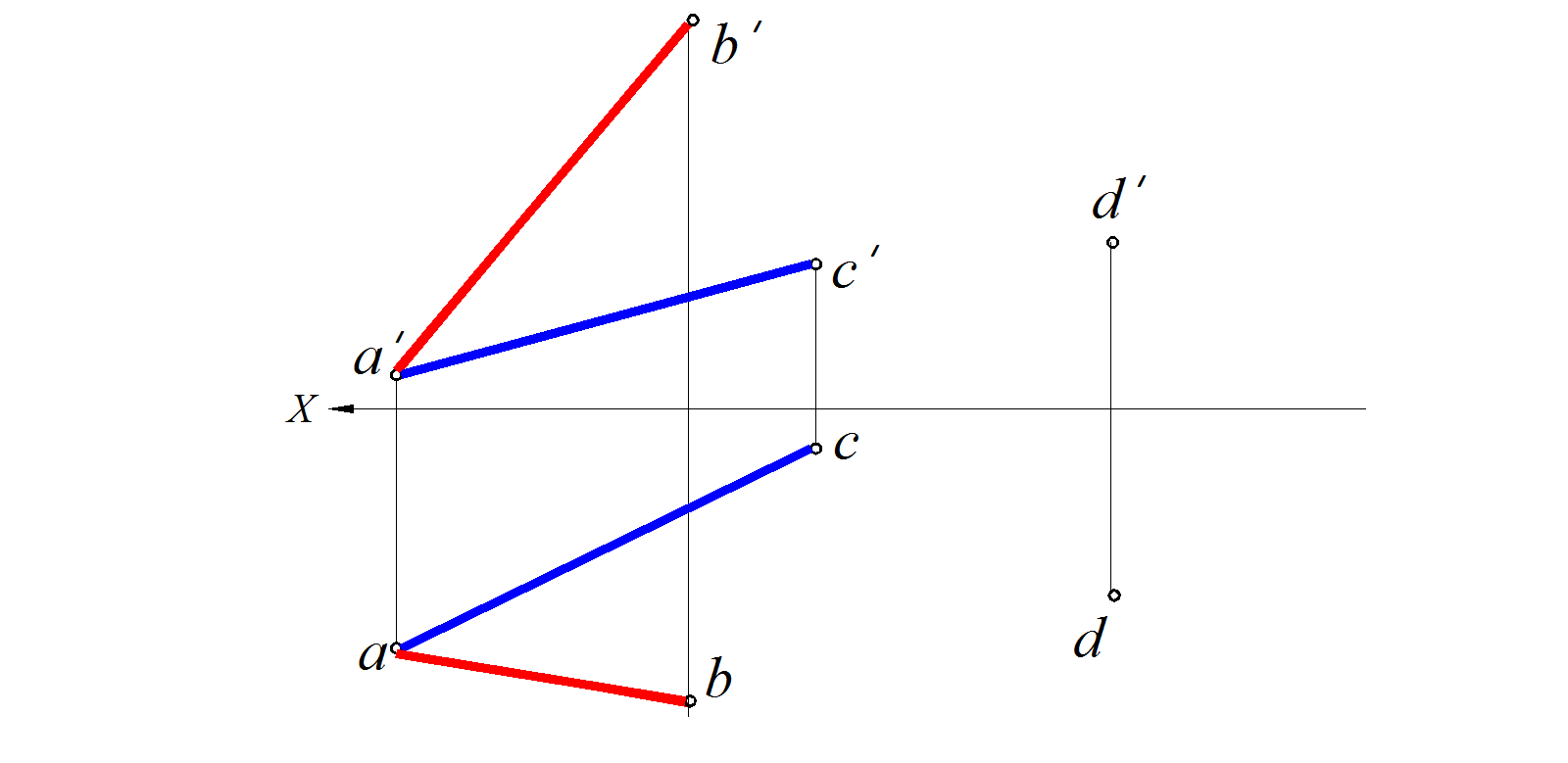
                                             Рис. 92. Условие задачи

 

 

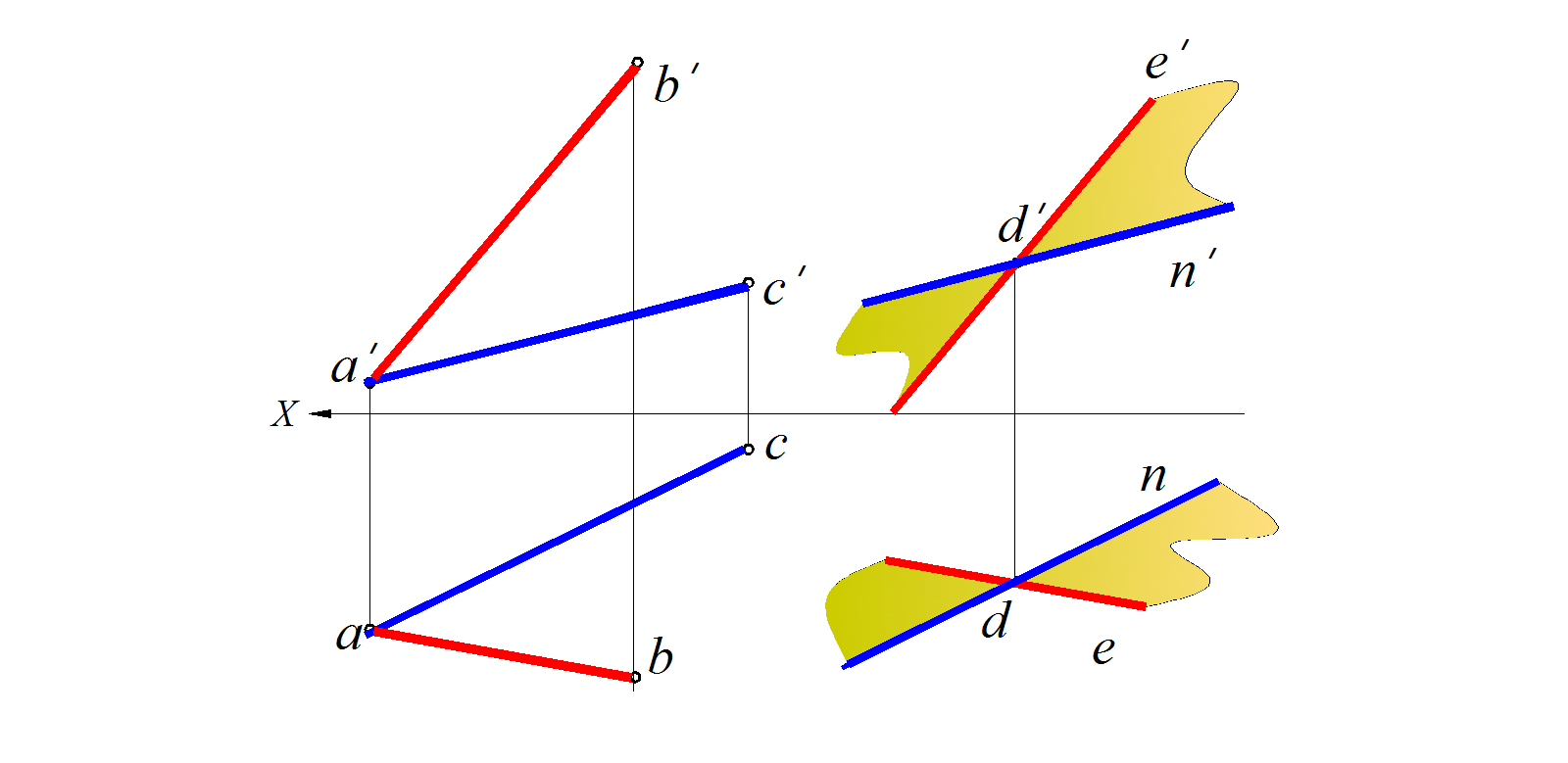
                              Рис. 93. Построение взаимно параллельных плоскостей

 

 

Задача.

Через точку А провести плоскость, параллельную плоскости Q , заданной следами (рис. 94).

      Решение:

Через точку А проведена плоскость Р параллельно заданной плоскости Q. Сначала через точку А проведена прямая AN, заведомо параллельная плоскости Р. Это горизонталь с проекциями an и a ' n ', причем an || P_H ,. Так как точка N является фронтальным следом горизонтали AN , то через эту точку пройдет след Q_V || P_V , а через Q_x – след Q_H || P_H . Плоскости Q и P взаимно параллельны, так как их одноименные пересекающиеся следы взаимно параллельны.

 

 

 

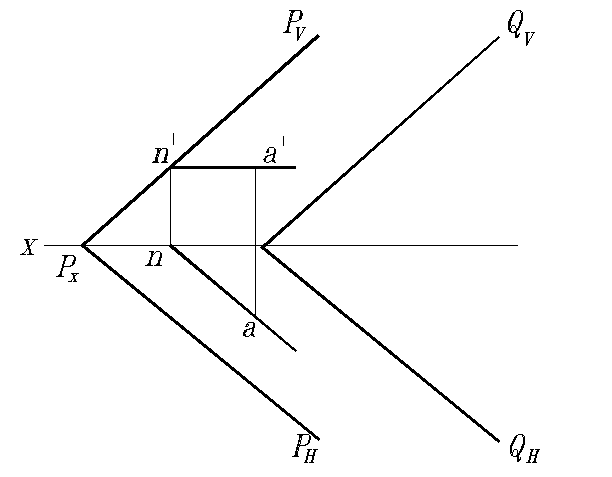
Рис. 94. Построение параллельных плоскостей, заданных следами

 

 

5. Способы преобразования чертежа

 

Метод замены плоскостей проекций. Метод вращения. Основные задачи, решаемые с применением способов преобразования чертежа.

Многие задачи решаются легко и просто, если прямые линии, плоские фигуры (основания, грани, ребра, оси) геометрических тел находятся в частном положении. В начертательной геометрии существует ряд методов, с помощью которых геометрические элементы общего положения переводятся в частное положение – это методы преобразования проекционного чертежа. Любое преобразование проекционного чертежа пред-ставляет собой связанную проективно цепочку геометрических образов, конечная пара в которой образует проекционную систему изображений, позволяющих с максимальной простотой реализовать решение задачи. В курсе начертательной геометрии рассматриваются, как правило, две группы методов – методы перемены плоскостей проекций и методы вращения. Рассмотрим их для преобразования чертежа прямой линии или плоской фигуры общего положения в чертеж с их частным положением.

При использовании метода перемены плоскостей проекций заданную систему плоскостей проекций заменяют на новую так, чтобы в ней исходные объекты оказались в частном положении, не меняя своего расположения в пространстве.

При методе вращения изменяют положение исходных объектов в пространстве так, чтобы они приняли частное положение относительно неизменных плоскостей проекций.

Рассмотрим более подробно указанные методы.

 

 

Все преобразования чертежа существуют для того, чтобы решение задачи стало более упрощенным. Это происходит в тех случаях, когда геометрические фигуры занимают частное положение относительно плоскостей проекций

Задача.

Решение

Анализируем графическое условие задачи: плоскость ΔABC – плоскость общего положения.

Для определения угла α заданной плоскости, необходимо преобразовать комплексный чертеж так, чтобы плоскость ΔABC стал фронтально проецирующей плоскостью в новой системе плоскостей.

Порядок выполнения графической части задачи:

1. Вводим новую плоскость проекции V₁: V₁ ⊥ H₁, V₁ ⊥ ΔABC.

2. Проводим в плоскости ΔABC горизонталь DC.

3. Ось проекции X₁ – горизонтальный след плоскости V₁ – проводим перпендикулярно прямой cd на любом расстоянии от точки d .

4. Проводим из точек a, b и d линии связи к новой оси X₁.

5. Откладываем от оси X₁ по линиям связи Z _С, Z _А, Z_В. Поскольку a ' принадлежит оси X, следовательно, a '₁ принадлежит OX₁.

 

   На новую плоскость проекций V₁ плоскость ΔABC отобразилась в впрямую линию, т. е. стала фронтально проецирующей плоскостью. На новой плоскости проекций V₁ угол наклона плоскости ΔABC к горизонтальной плоскости проекций α отображен без искажения (рис. 32).

 

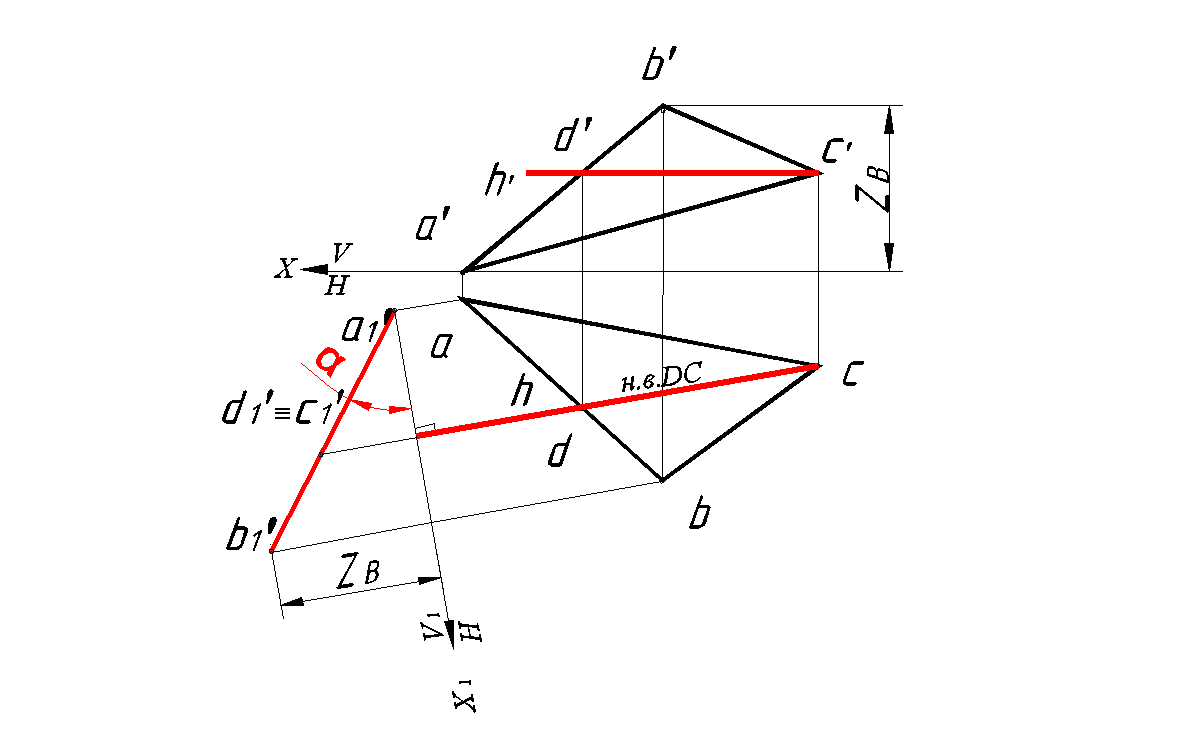
Рис. 105. Определение угла ∠α плоскости ∆АВС

Задача 2.

Определить угол наклона плоскости общего положения к фронтальной плоскости проекций – угол β

Решение:

Для определения угла β заданной плоскости необходимо преобразовать комплексный чертеж так, чтобы плоскость ΔABC стал горизонтально проецирующей плоскостью в новой системе плоскостей.

1. Вводим новую плоскость проекции Н₁: H₁ ⊥ V, Н₁ ⊥ ΔABC.

2. Проводим в плоскости ΔABC фронталь DC.

3. Ось проекции X₁ – фронтальный след плоскости Н₁, проводим перпендикулярно прямой c ′ d ′ на любом расстоянии от точки с ′.

4. Проводим из точек а ′,  b ′ , и d ′ линии связи к новой оси X₁.

5. Откладываем от оси X₁ по линиям связи У_С, У_А, У_В. Поскольку a ′ принадлежит оси X, a₁ принадлежит OX₁.

На новую плоскость проекций Н₁ плоскость ΔABC отобразилась в прямую линию, т. е. стала горизонтально проецирующей плоскостью. На новой плоскости проекций Н₁ угол наклона плоскости треугольника АВС к фронтальной плоскости проекций β отображен без искажения (рис. 106).

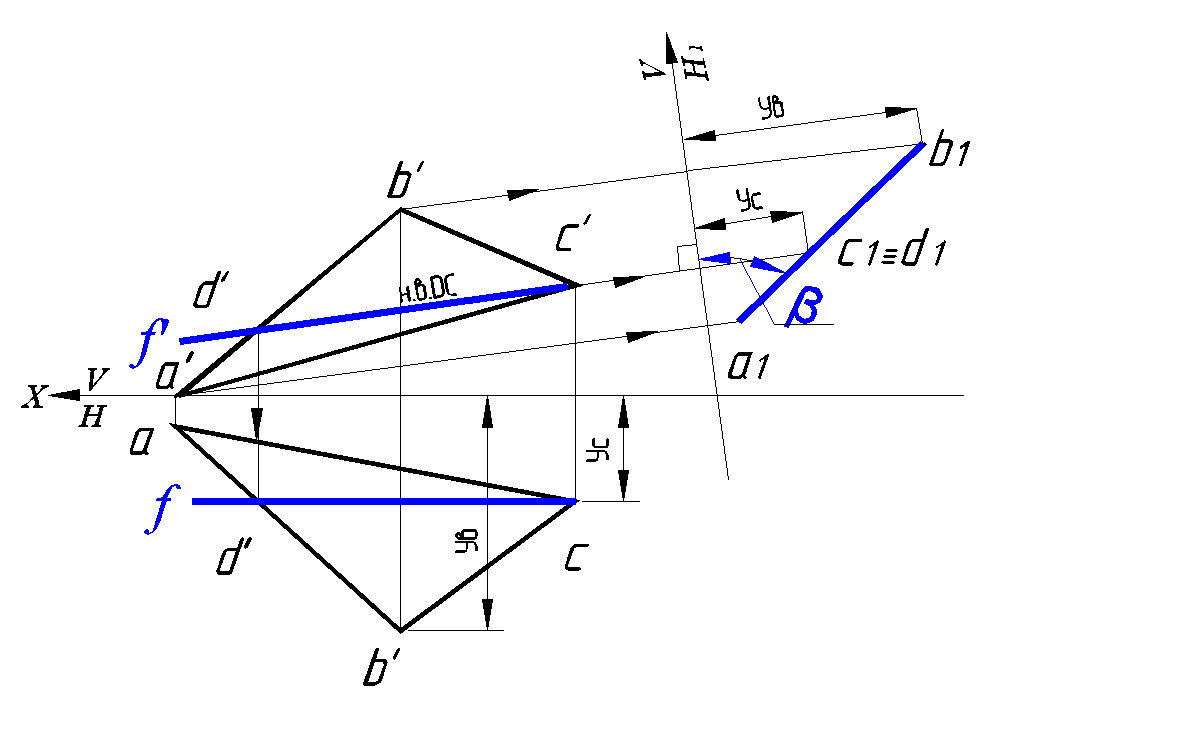
Рис. 106. Определение ∠β плоскости ∆АВС

4. Преобразование плоскости проецирующего положения в плоскость уровня (Определение натуральной величины плоской фигуры)

    Для определения натуральной величины плоской фигуры необходимо преобразовать комплексный чертеж так, чтобы проецирующая плоскость в новой системе плоскостей стала плоскостью уровня.

 

 Задача.

 Преобразовать комплексный чертеж так, чтобы плоскость Δ ABC стала фронтальной плоскостью уровня.

   Решение:

Анализируем графическое условие задачи: плоскость ΔABC – горизонтально проецирующая плоскость

1. Вводим новую плоскость проекции V₁. Условия ввода плоскости V₁: V₁ ⊥ H₁, V₁ ⊥ ΔABC .

2. Ось проекции X₁ – горизонтальный след плоскости V_1. Проводим ось X₁ параллельно горизонтальной проекции плоскости ΔABC на любом расстоянии от нее.

3. Проводим из точек a, b, и c линии связи (перпендикуляры к оси X₁).

4. Откладываем Z _С, Z _А, Z_В по линиям связи соответственно точкам A, B, C от оси X₁.

5. Получаем очки a₁′, b₁′, c₁′ . Соединяя полученные точки, получим новую проекцию плоскости ΔABC равную натуральной величине ΔABC .

 Следовательно, в новой системе плоскостей плоскость занимает положение фронтальной плоскости уровня (рис.107).

 

 

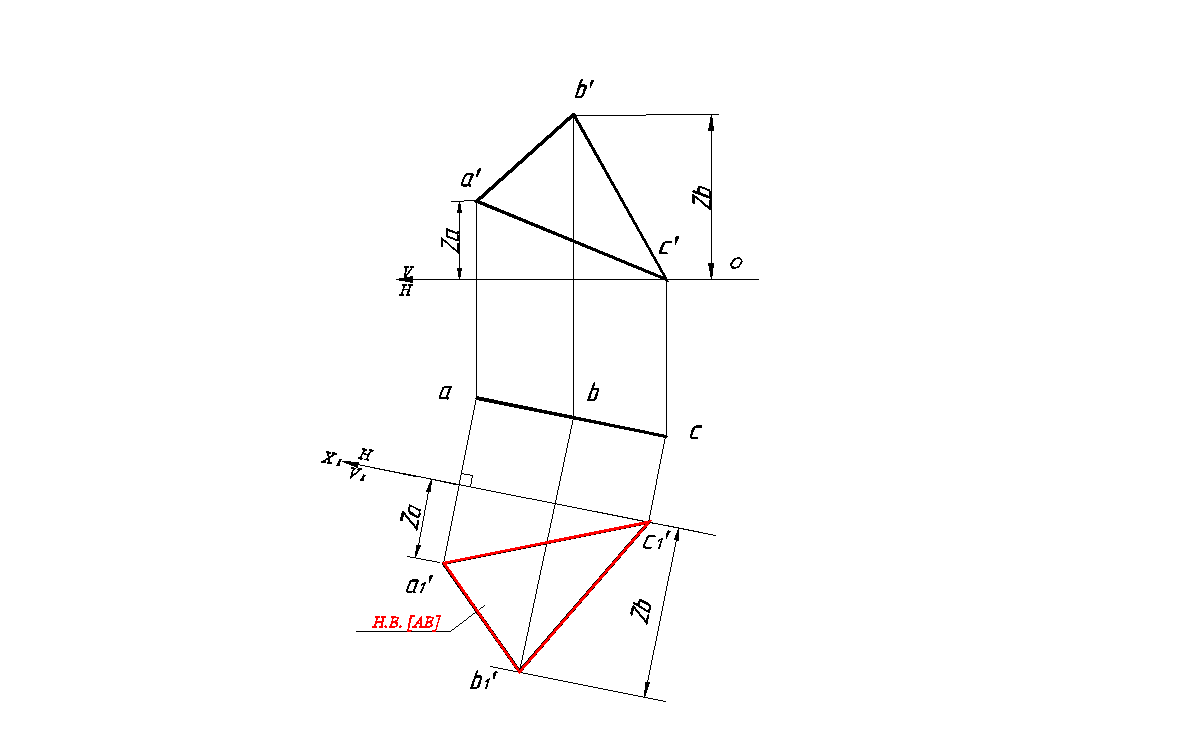
Рис. 107. Преобразование горизонтально проецирующей плоскости во фронтальную плоскость уровня

Задача.

Метод вращения

 

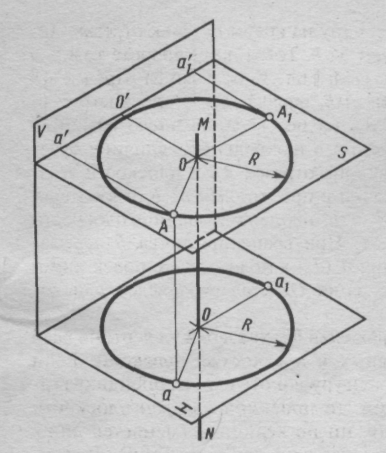
Суть метода заключается в том, что геометрический элемент вращается (перемещается) относительно неподвижных плоскостей проекций, занимая необходимое частное положение. Каждая точка вращаемого элемента перемещается в плоскости (плоскость вращения) перпендикулярной к некоторой неподвижной прямой (оси вращения) по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра (радиус вращения).

Итак, для применения способа вращения в целях преобразования чертежа отметим следующие четыре элемента (рис. 109): ось вращения MN; плоскость вращения точки S _┴ MN; центр вращения S ∩ MN = О; радиус вращения R = | OA |.

 

Рис. 109.  Вращение точки вокруг оси

 

В качестве оси вращения обычно используют прямые, перпендикулярные или параллельные плоскостям проекций. Кроме того, ось может быть задана или выбрана, указана или нет. В зависимости от этого рассматривают различные способы:

– вращение вокруг оси, перпендикулярной к плоскости проекций;

– вращение без указания осей вращения или плоскопараллельное перемещение;

– вращение вокруг прямых, параллельных плоскости проекций;

– вращение плоскости вокруг следа (метод совмещения).

 

Плоскостям проекций

Механизм этого метода удобно рассматривать на примере вращения точки вокруг проецирующей прямой.

Точка А вращается вокруг горизонтально-проецирующей оси MN (рис. 110). Плоскость вращения S параллельна плоскости Н и на фронтальной проекции изображена следом S_V. Окружность, описанная в пространстве точкой А, проецируется на плоскость Н без искажения. Горизонтальная проекция центра вращения О совпадает с горизонтальной проекцией оси MN, а горизонтальная проекция оа радиуса вращения является его натуральной величиной.  Поворот точки А произведен на угол φ против часовой стрелки так, чтобы в новом положении точки А₁ радиус вращения был параллелен плоскости V .

 

 

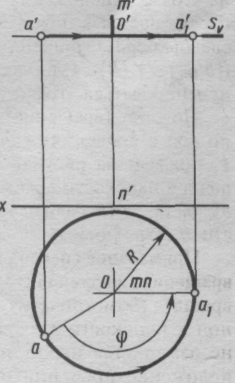
Рис. 110. Вращение точки вокруг горизонтально-проецирующей оси

 

Если точку вращать вокруг фронтально-проецирующей оси, то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная – по прямой параллельно оси х.

Вращение точки вокруг проецирующей прямой применяют при решении некоторых задач. Рассмотрим некоторые из них в качестве примеров.

 

Многогранники

Общие характеристики многогранников. Правильные многогранники (тела Платона). Изображение многогранников на чертеже. Пересечение многогранников плоскостью и прямой. Алгоритм решения задачи. Взаимное пересечение многогранников. Развертки: способ триангуляции, нормального сечения, раскатки.

Нелинейчатые поверхности

Эти поверхности могут быть с образующей переменного или постоянного вида. Широкое применение в инженерной практике получили нелинейчатые поверхности с переменной образующей – каналовые и циклические.

Каналовой называют поверхность, образованную непрерывным перемещением замкнутых плоских сечений (не окружностей) по криволинейной направляющей. Площади этих сечений могут оставаться постоянными или монотонно изменяться в процессе перехода от одного сечения к другому. Чаще эти сечения (P₁, P₂…) параллельны некоторой плоскости или перпендикулярны к направляющей линии m (рис. 132, а).

Циклические поверхности образуются с помощью окружности, центр которой перемещается по криволинейной направляющей. В процессе движения радиус окружности монотонно меняется (рис. 132, б).

Циклическую поверхность можно рассматривать как частный случай каналовой поверхности.

Частным же случаем циклической поверхности является трубчатая поверхность. Здесь образующая – окружность – остается постоянной в процессе перемещения по криволинейной направляющей; плоскость окружности все время остается перпендикулярной к направляющей. Следовательно, трубчатую поверхность можно отнести и к классу по­верхностей с постоянной образующей.

 

           а                                                                б

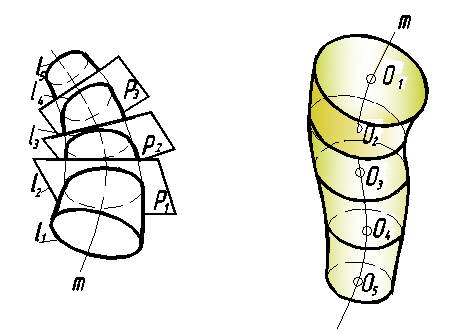
Рис. 132. Нелинейчатые поверхности с переменной образующей:

а – каналовые; б – циклические

 

 

 

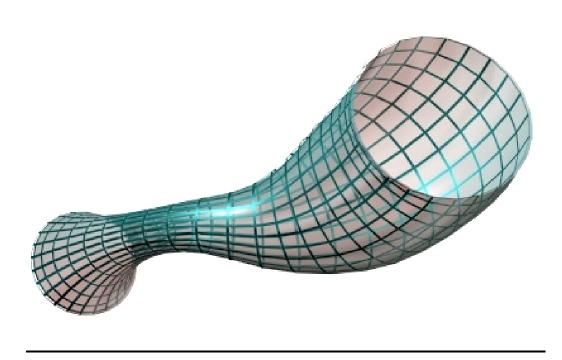
Рис. 133. Нелинейчатые поверхности с переменной образующей:

а – циклическая ; б – трубчатая

 

Винтовые поверхности

Поверхность называется винтовой, если она получается винтовым перемещением образующей. В зависимости от формы образующей винтовые поверхности могут быть линейчатыми и нелинейчатыми. Определитель этой поверхности имеет вид:

 

(a , m) ; [A].

 

Геометрическая часть определителя – образующая a, направляющая винтовая линия m; алгоритмическая часть – А – дополнительные указания о характере винтового перемещения образующей а.  

 

 

Рис. 134. Винтовая поверхность

 

Наибольшее применение имеют винтовые поверхности с прямолинейной образующей и направляющей – винтовой линией постоянного шага. Такие поверхности называют геликоидами. Их характерной особенностью является постоянство угла наклона прямолинейной образующей к направляющей плоскости, за которую принята плоскость, перпендикулярная оси винтовой поверхности. В зависимости от величины этого угла геликоиды называют прямыми (угол равен 90°) и косыми или наклонным (угол произвольный – отличный от 0 и 90°). Чертеж прямой винтовой поверхности приведен на рис. 135, а. По своему образованию эта поверхность является коноидом, т. к. образующая АВ – прямая линия; она во всех положениях параллельна некоторой плоскости (в данном случае перпендикулярной оси винтовой линии); образующая пересекает две направляющие линии, кривую и прямую (ось) и движется вдоль оси вверх. Так как кривая направляющая представляет винтовую линию, то такой коноид называется винтовым или прямым геликоидом.

Изображение косой винтовой поверхности – косого геликоида – приведено на рис. 135, б. Проекции отрезка АО – образующей – изображены в ряде последовательных положений. Точка А перемещается по винтовой линии. Соответствующие положения проекций точки О отмечают на оси, руководствуясь тем, что проекция отрезка АО на ось вращения постоянна по величине (l).

а                                                                  б

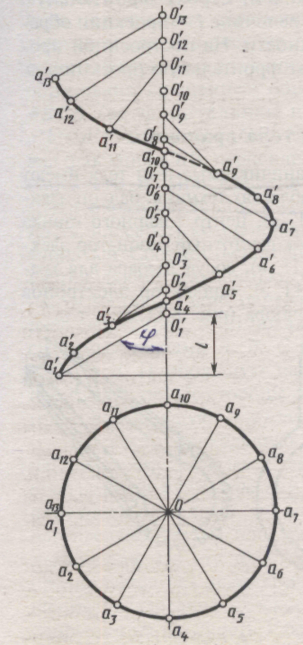
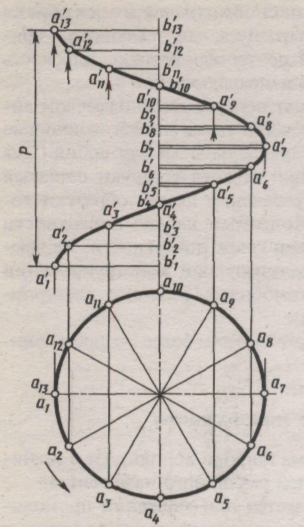
Рис. 135. Геликоид:

а – прямой; б – косой

Поверхности вращения

В числе кривых поверхностей – линейчатых и нелинейчатых – можно выделить обширный класс поверхностей вращения, объединенных одним законом образования. Это поверхности, получаемые при вращении какой-либо образующей (прямой, кривой, плоской или пространственной) вокруг неподвижной прямой – оси вращения.

 

Широкое применение поверхности вращения и ограничиваемые ими тела получили в технике, что объясняется распространенностью вращательного движения и простотой обработки их на станках. Типичными представителями этих поверхностей служат и гончарные изделия. Их образующие, как правило, плоские кривые линии. В состав определителя поверхности вращения входят: образующая m и ось вращения i (рис. 136, а). Каждая точка (А, В, С) образующей m при вращении вокруг оси i описывает окружность, называемую параллелью (рис. 136, б). Самую большую параллель называют экватором (на ней находится точка C), наименьшую (ее описывает точка В) – горлом.

Плоскости, проходящие через ось поверхности вращения, называются меридиональными, а линии, по которым они пересекают поверхность, меридианами. Меридиональную плоскость, параллельную плоскости проекций, называют главной меридиональной плоскостью Р (след Р_Н), а линию пересечения ее с поверхностью вращения – главным меридианом.

Положение точки на поверхности вращения определяется при помощи параллели, проходящей через эту точку. Но это не исключает возможности применять прямолинейные образующие в случае линейчатых поверхностей вращения.

На рис. 136, б на экваторе показаны точка C. Границей видимости точек на фронтальной плоскости служит плоскость главного меридиана Р. С – граничная точка, находится на главном меридиане;

 

 

 

 

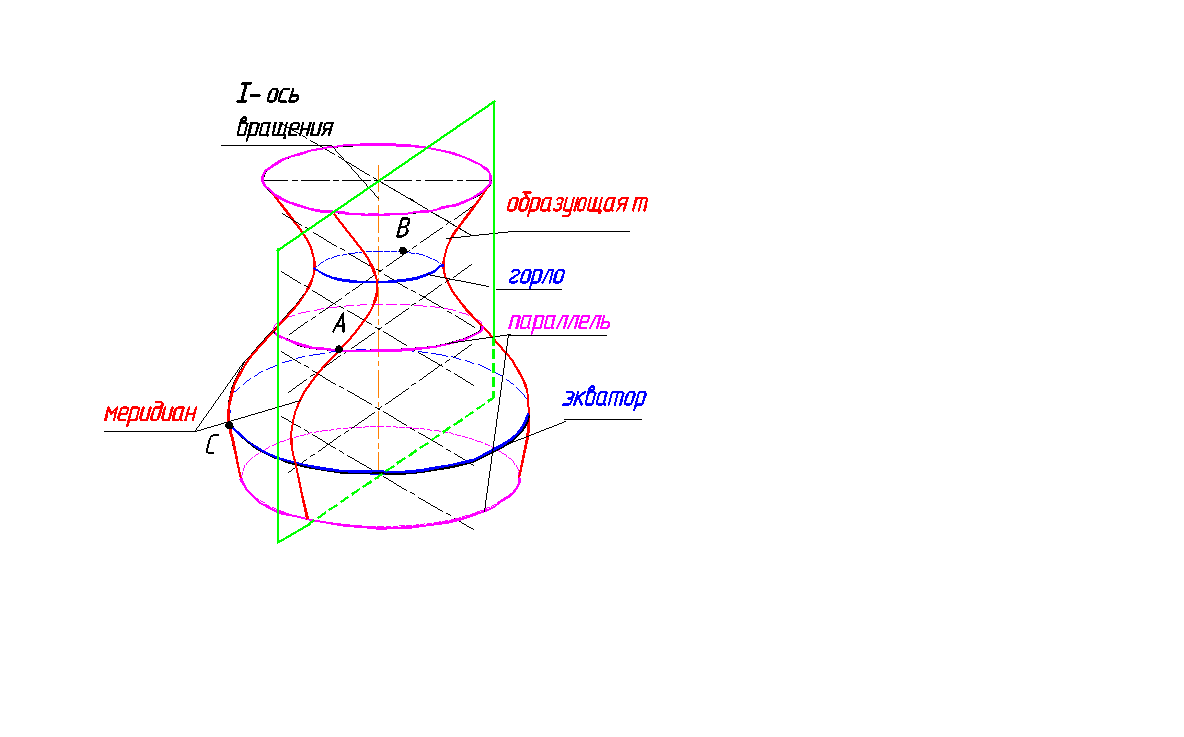
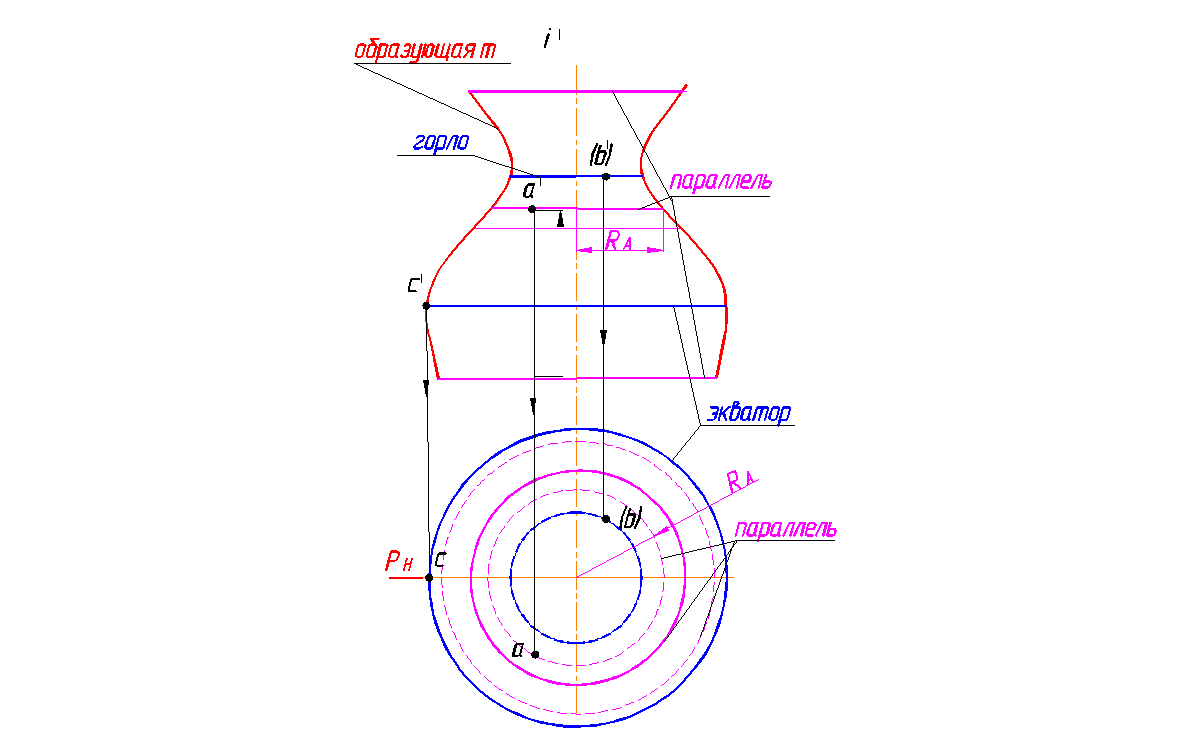
Рис. 136. Поверхность вращения

 

Наиболее удобными для выполнения изображений поверхностей вращения являются случаи, когда их оси перпендикулярны какой-либо плоскости проекций.

Наибольшее распространение получили поверхности вращения – алгебраические второго и четвертого порядка. Рассмотрим некоторые из них.

Тор – поверхность 4-го порядка, образованная вращением окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр.

Разновидности тора: открытый или круговое кольцо (рис. 137, 138); самопересекающийся – окружность пересекает ось (рис. 139); закрытый – окружность касается оси (рис. 140); глобоид - образующей этой поверхности является дуга окружности, ось вращения которой располагается вне очерка окружности с наружной стороны (рис. 141).

Точки на поверхности тора, как и для всех поверхностей вращения, определяют по принадлежности их его параллелям. При этом надо иметь ввиду, что в плоскостях перпендикулярных оси тора, есть два семейства параллелей: линии пересечения плоскостей с наружной поверхностью (точки А и D лежат на такой параллели на рис. 138) и линии пересечения плоскостей с внутренней поверхностью тора (точки В и С).

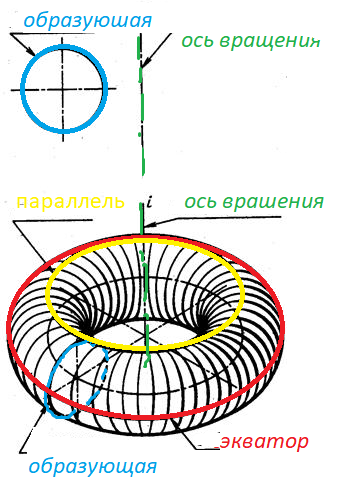
Рис. 137. Тор открытый – пространственная модель

 

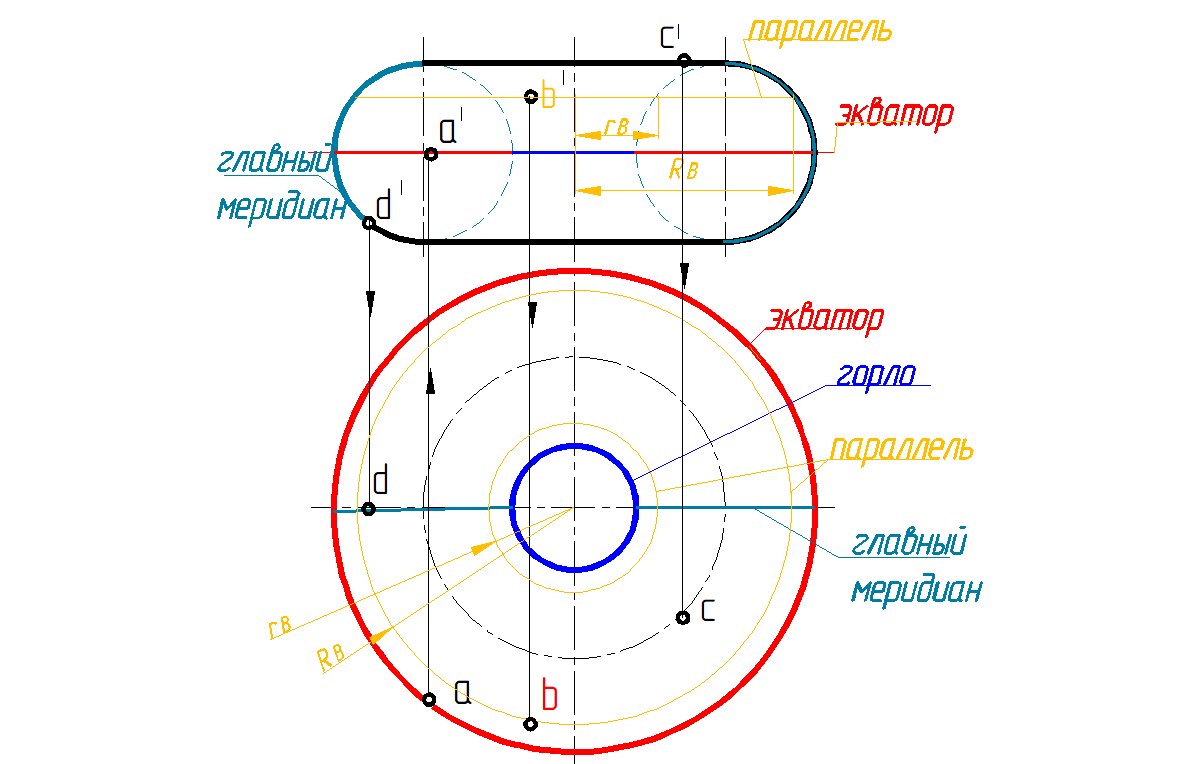
Рис. 138. Тор открытый на эпюре Монжа

 

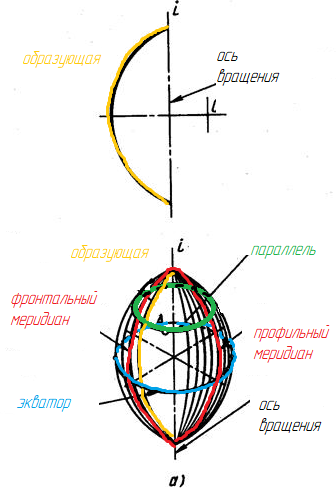
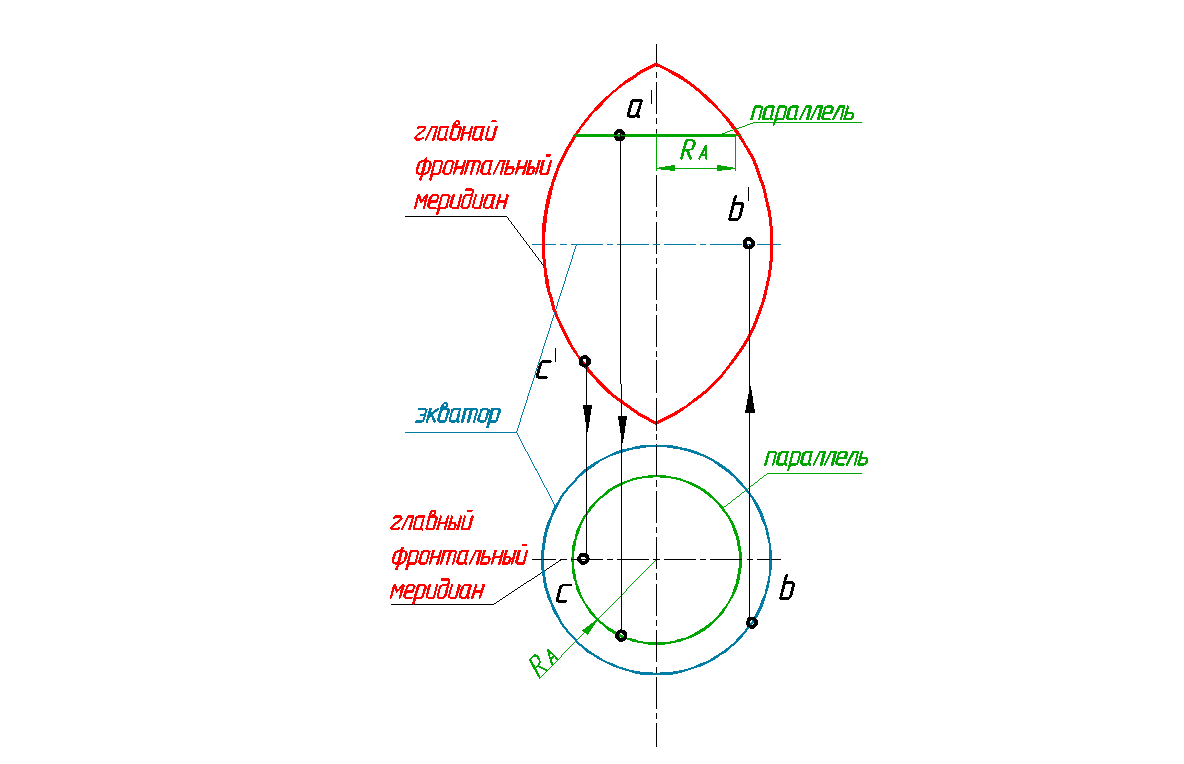
Рис. 139. Самопересекающийся тор

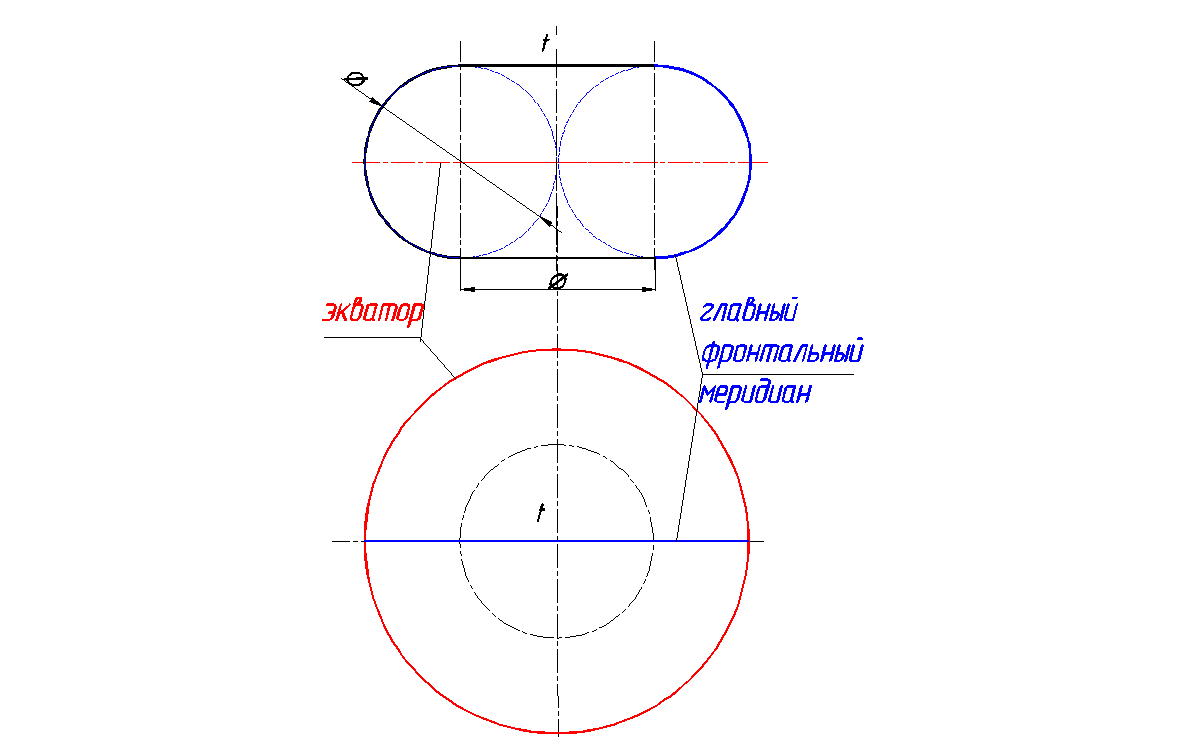
Рис. 140. Закрытый тор

 

 

 

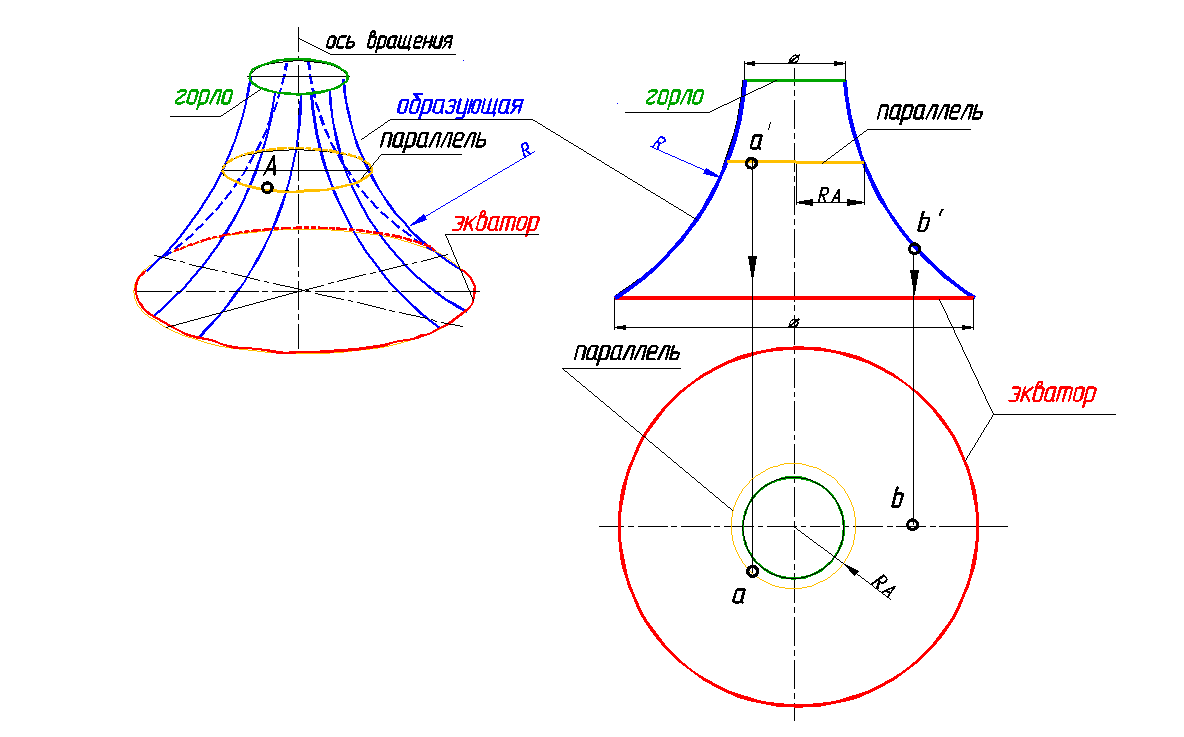
Рис. 141. Глобоид

 

 

Поверхности вращения 2-го порядка образуются вращением кривой 2-го порядка вокруг своей оси: сфера, эллипсоид, гиперболоид, параболоид.

 

Сфера

 

Сфера – поверхность, образующей которой является окружность   с центром на оси вращения (рис. 142). Геометрическое тело, полученное вращением полукруга вокруг диаметра, который одновременно является осью вращения, называется шapом.

Каждая точка поверхности сферы удалена от ее центра на одинаковое расстояние. Если любую точку, принадлежащую поверхности, соединить   с центром сферы, то этот отрезок будет радиусом сферы R.

Если через центр сферы прямой линией соединить две точки, принадлежащие поверхности, то этот отрезок будет диаметром сферы.

 

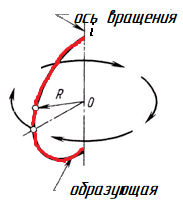
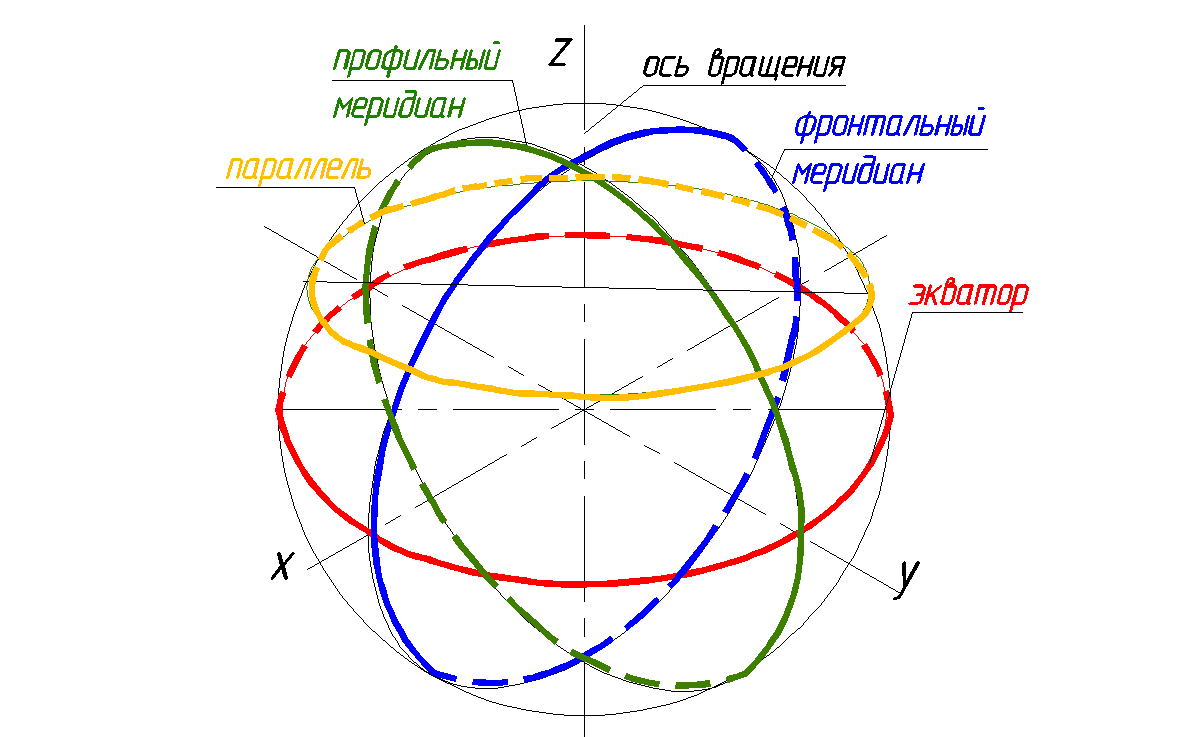
Рис. 142. Сфера

 

 

ОСНОВНЫЕ ПОНЯТИЯ ОБ ОБОБЩЕННЫХ ПОЗИЦИОННЫХ ЗАДАЧАХ

Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности) геометрическим фигурам.

Позиционные задачи занимают важное место в начертательной геометрии. Ранее мы рассматривали такие задачи, связанные с нахождением точки пересечения прямой линии с плоскостью и построением линии пересечения плоскостей. Теперь рассмотрим способы решения позиционных задач с участием кривых линий и поверхностей. Эти задачи называют обобщенными. Задачи с участием прямых линий и плоскостей являются их частными случаями. В общем же случае эти задачи формулируют так:

Построить точки пересечения:

1) плоскости с поверхностью

2) линии с поверхностью

3) поверхности с поверхностью

Задача.

По заданной фронтальной проекции сферы с вырезом построить горизонтальную и профильную проекции (рис. 149).

Решение:

1.Анализ графического условия:

Вырез сферы выполнен плоскостями Р1 и Р2, которые пересекают сферу по окружности. Но эти плоскости перпендикулярными фронтальной плоскости проекций. Поэтому линии пересечения (окружности) на этой плоскости проекций на чертеже отражаются отрезками. Плоскость Р1 пересекая сферу по окружности, отображается на горизонтальной и профильной проекции в виде эллипса Фронтально-проецирующая плоскость Р2 является еще и профильной плоскостью уровня, то есть параллельна профильной плоскости проекций. Поэтому отображается на профильной плоскости проекций без искажения – в виде окружности.

2.Строим характерные точки, лежащие на экваторе –точка В, главном фронтальном меридиане –точки А и Е и главном профильной меридиане- точка С.

3.Строим случайные точки, используя параллели сферы (например, точку N). Соединяем построенные точки, устанавливая при этом видимость линий.

4.Очерк сферы на горизонтальной проекции определяет линия экватора

от точки d до точки d и от точки b до точки b .

5.Очерк сферы на профильной проекции определяет линия главного профильного меридиана от точки с до точки с

 

 

 

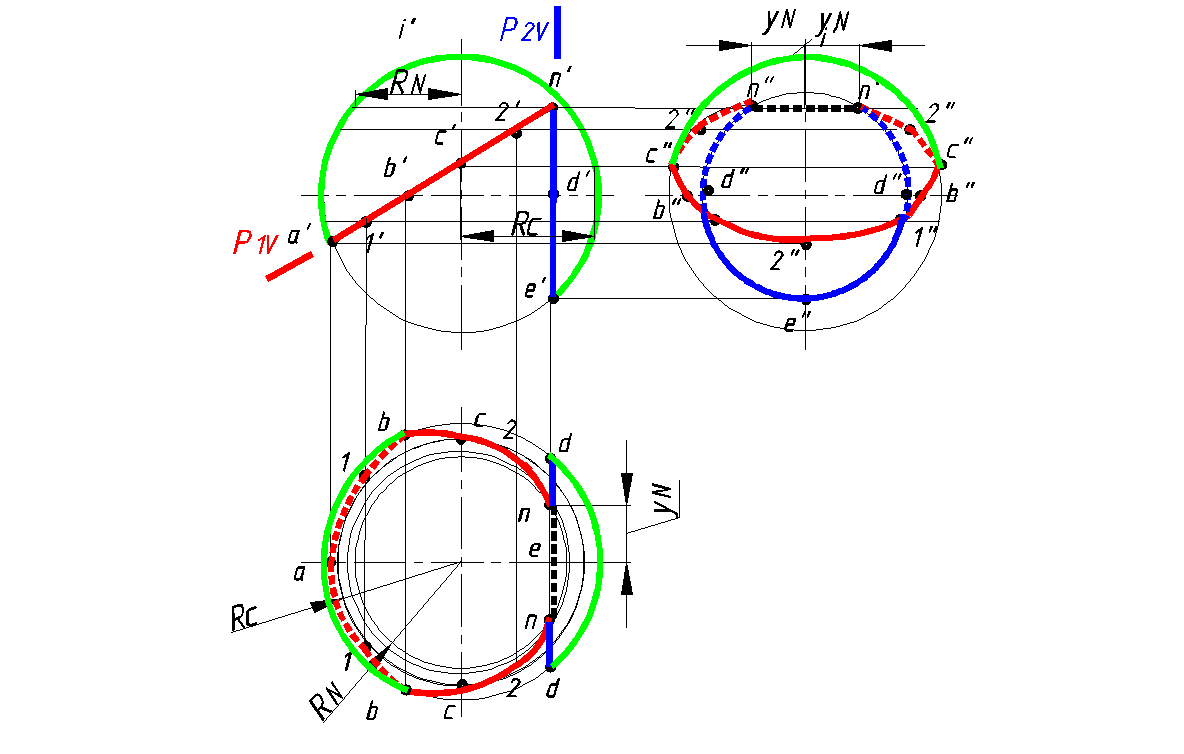
Рис. 149. Сфера с вырезом

 

 Пересечение тора плоскостью

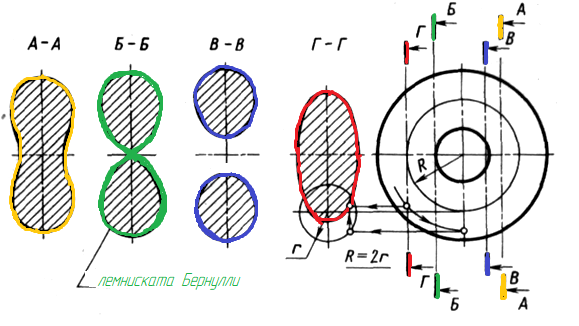
Тор- алгебраическая поверхность четвертого порядка. При пересечении тора плоскостью получаются плоские алгебраические кривые 4-го порядка, общее название которых – кривые Персея (в честь геометра Древней Греции). Вид кривых зависит от расстояния секущей плоскости до оси тора (рис. 150).

Кроме того, тор имеет три семейства окружностей:

Первое - секущие плоскости, проходят через ось тора. В сечении получаются две окружности – образующие тора (меридианы)

 Второе - секущие плоскости проходят перпендикулярно оси вращения. В сечении получаются две окружности – параллели.

 Третье –секущая плоскость качается двух окружностей главного меридиана смешанным образом. В сечении получаются две окружности –круги Вилларсо

 

Рис. 150. Сечения тора – кривые Персея

 

 

Задача.

По заданной фронтальной проекции тора с вырезом построить его горизонтальную проекцию (рис. 151).

Решение:

1.Анализ графического условия:

Вырез тора выполнен плоскостями Р 1 и Р 2. Плоскость Р1 пересекает тор по окружностям радиуса R A и R B .  Эта плоскость перпендикулярна фронтальной плоскости проекций. Поэтому линии пересечения (окружности) на этой плоскости проекций на чертеже отражаются отрезками. Плоскость Р 1 пересекая тор по окружностям, отображается на горизонтальной в виде окружности, так как она является горизонтальной плоскостью уровня. Фронтально проецирующая плоскость Р 2 рассекает тор по кривой Персея, которая отображается на горизонтальной плоскости проекций с искажением

2.Строим характерные точки, лежащие на экваторе и на горле–точка D, главном фронтальном меридиане –точки А, В и N и главном профильной меридиане- точка С.

3.Строим случайные точки, используя параллели тора (например, точку 3). Соединяем построенные точки, устанавливая при этом видимость линий.

4. На горизонтальной проекции определяем очерк тора, оставшийся после выреза. Очерк тора на горизонтальной проекции определяется линией экватора. Линия экватора осталась после выреза от точки D с правой стороны оси вращения. Поэтому на горизонтальной проекции линия экватора определяется от точки d до точки d .

 

 

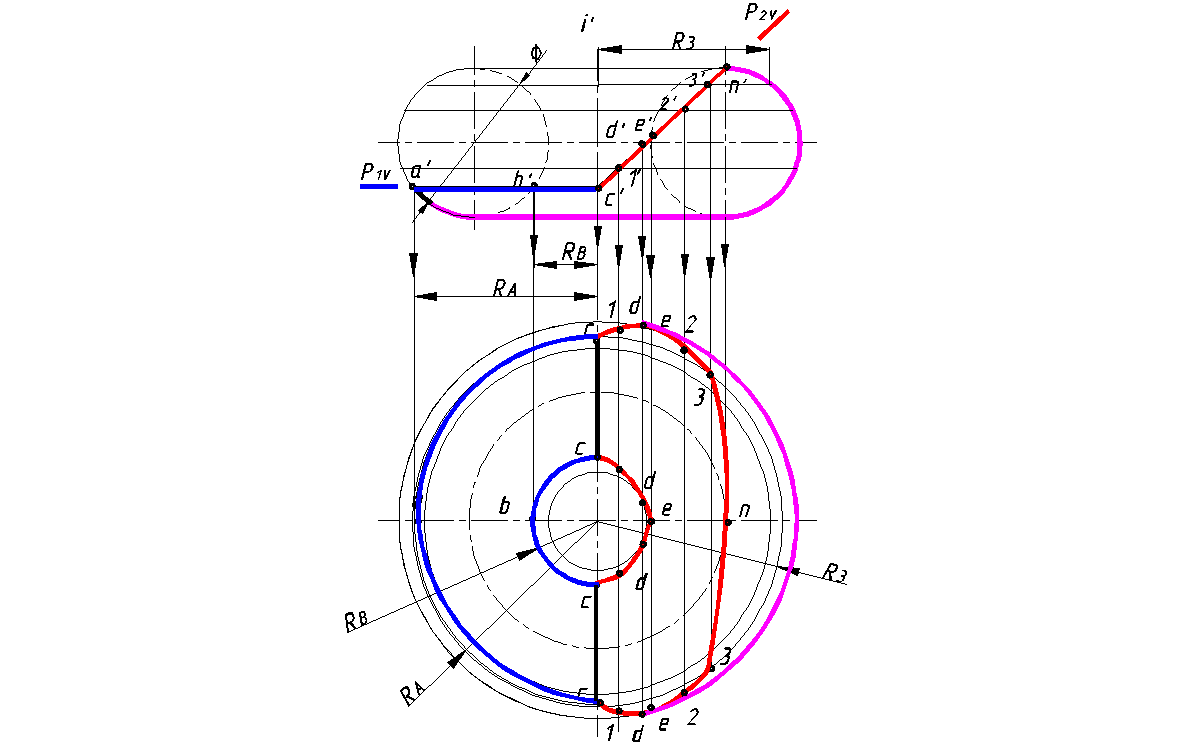
Рис. 151. Построение тора с вырезом

 

Задача.

Определить точки пересечения сферы с фронтально-проецирующей прямой АВ (рис. 153, б).

 

Решение

Так как прямая занимает положение, перпендикулярное плоскости V, то фронтальные проекции искомых точек m ' и n ' совпадут с фронтальной проекцией самой прямой. Горизонтальные проекции точек m и n находим из условия принадлежности их сфере при помощи соответствующих параллелей.

Задача.

Определить точки пересечения прямой общего положения АВ с поверхностью пирамиды (рис. 154).

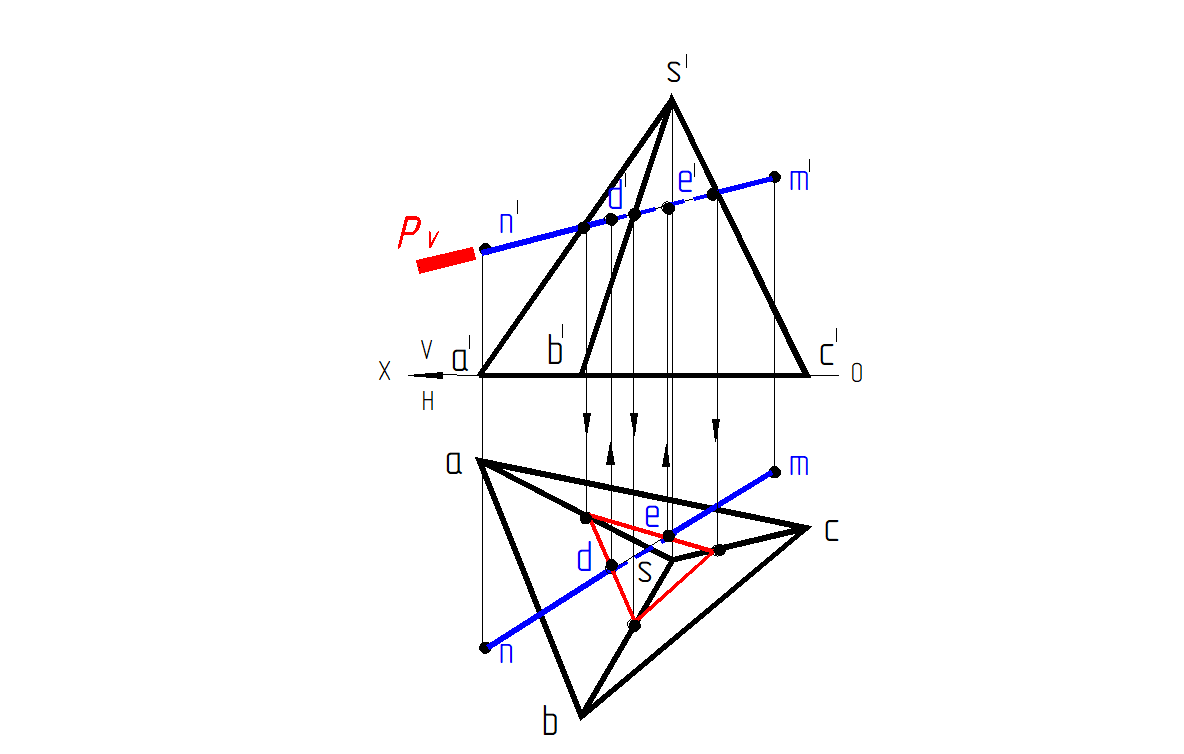
Рис. 154. Определение точек пересечения прямой с поверхностью пирамиды

 

Решение:

1. Через прямую MN фронтально проецирующую плоскость Р (след Р V)

2. Строим сечение пирамиды и проведенной плоскости Р

3. Находим искомые точки D и Е как точки пересечения построенного сечения и заданной прямой

4. Определяем видимость прямой MN относительно пирамиды

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

 

В результате решения таких позиционных задач определяется линия пересечения поверхностей, все точки которой одновременно принадлежат обеим поверхностям. Порядок линии пересечения алгебраических поверхностей равен произведению порядков этих поверхностей.

Построение линии пересечения поверхностей является наиболее распространенной задачей в инженерной практике. Рассмотрим способы их построения, которые встречаются наиболее часто.

Решение задачи всегда начинают с анализа условия, выясняя: какие поверхности пересекаются; какое положение они занимают относительно плоскостей проекций и друг друга; какие линии должны получиться в пересечении поверхностей (плоские, пространственные, характер проекций линии). После этого выбирают рациональный способ решения.

При построении точек линии пересечения поверхностей при любом способе вначале находят те точки, которые называют характерными или опорными:

– принадлежащие очеркам данных поверхностей;

– наиболее удаленные на экстремальное расстояние (min и max) от плоскостей проекций – ближняя и дальняя; высшая и низшая; крайняя левая и правая;

– определяющие границы видимости проекций кривой.

Затем находят промежуточные точки искомой линии.

Построенные точки соединяют между собой, учитывая характер линии пересечения и ее проекций. Следует иметь в виду, что проекции линии пересечения поверхностей должны всегда быть в пределах контура наложения проекций этих поверхностей.

Определяют видимость проекций линии пересечения и взаимную видимость поверхностей.

 

Построение линии пересечения поверхностей,

когда одна из них (или обе) является проецирующей

К проецирующим поверхностям относят плоскости частного положения или цилиндрические поверхности, образующие которых перпендикулярны какой-либо плоскости проекций. Они обладают свойством: все точки, принадлежащие им, проецируются на их следы. Значит одна из проекций (или две) линии пересечения известна – она совпадает со следом проецирующей поверхности.

Задача.

Построить линию пересечения цилиндров вращения

Решение:

1. Анализ графического условия задачи: у пересекающихся цилиндров (рис. 9) поверхности являются проецирующими: горизонтально проецирующей и профильно проецирующей. Линия пересечения будет представлять пространственную кривую 4-го порядка. Горизонтальная проекция отобразится на след горизонтально-проецирующего цилиндра (окружность), а профильная – на след профильно-проецирующего цилиндра.

2. Т. к. поверхности имеют общую фронтальную плоскость симметрии, их фронтальная проекция будет представлять гиперболу (две конкурирующие ветви), которую строим по общему правилу построения кривой линии по точкам, когда две проекции точек известны.

 

 

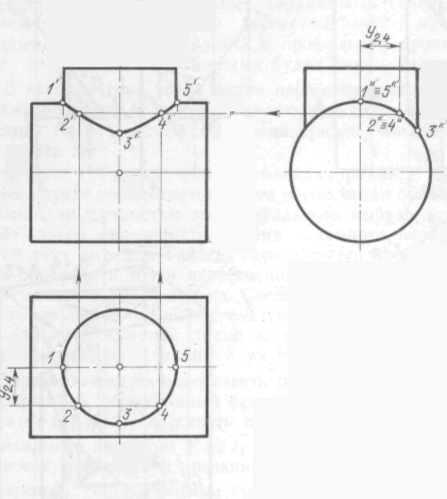
Рис. 155. Пересечение двух проецирующих цилиндров

 

Задача.

Построить линию пересечения заданных поверхностей

Решение:

1. Анализ графического решения задачи (рис. 155):

Цилиндр занимает фронтально проецирующее положение.Фронтальная проекция – окружность – совпадает с фронтальным следом цилиндрической поверхности. Горизонтальную и профильную проекции линии пересечения строим по множеству точек, исходя из условия их принадлежности непроецирующей поверхности (в данном случае конической), используя ее параллели.

2. Начинаем построение с характерных точек: 1, 2, 3, 4, 5, 6. Точки 1 и 6 принадлежат фронтальной образующей конуса; 3 – горизонтальной образующей цилиндра; 2 и 4 – профильным образующим конуса; 5 – профильной образующей цилиндра.

Точка К – одна из промежуточных точек.

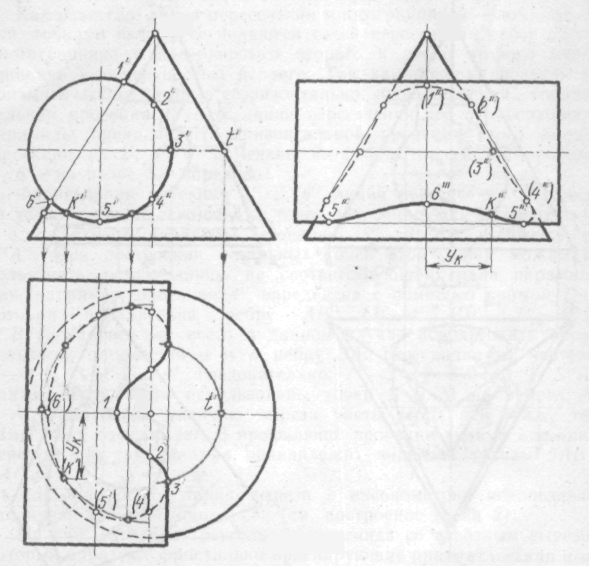
3. Построенные горизонтальные и профильные проекции точек соединяем плавными кривыми, устанавливая при этом их видимость и видимость образующих поверхностей.

Рис. 155. Построение линии пересечения конуса с проецирующим цилиндром

Построение линии пересечения поверхностей, когда

ни одна из поверхностей не является проецирующей

 

В этом случае применяют общий способ построения линии пересечения, который заключается в использовании вспомогательных секущих поверхностей-посредников.

Сформулируем общее правило построения линии пересечения поверхностей:

1) выбирать вид вспомогательных поверхностей;

2) построить линии пересечения вспомогательных поверхностей с заданными поверхностями;

3) найти точки пересечения построенных линий и соединить их между собой плавной кривой.

В качестве вспомогательных поверхностей выбирают такие, линии пересечения которых с заданными поверхностями проецируются на чертеж в графически простые линии – прямые, окружности. В качестве вспомогательных поверхностей можно, например, использовать плоскости или сферы. Рассмотрим их применение.

Задача.

Задача.

Построить линию пересечения заданных поверхностей (рис. 166)

 

Решение :

1. Анализ графического условия: заданые поверхности вращения конус и цилиндр имеют общую фронтальную плоскость симметрии. В обе поверхности вписана сфера. Поэтому линия персечения на фронтальной

проекции распадается на две плоские кривые второго порядка - два эллипса.

2. Горизонтальную проекцию линию персечения находим из принадлежности к поверхности конуса, привязывая точки параллелями.

3. Соединяем точки персечения плавной кривой, определяя ее видимость.

4. Определяем взаимную видимость поверхностей

 

 

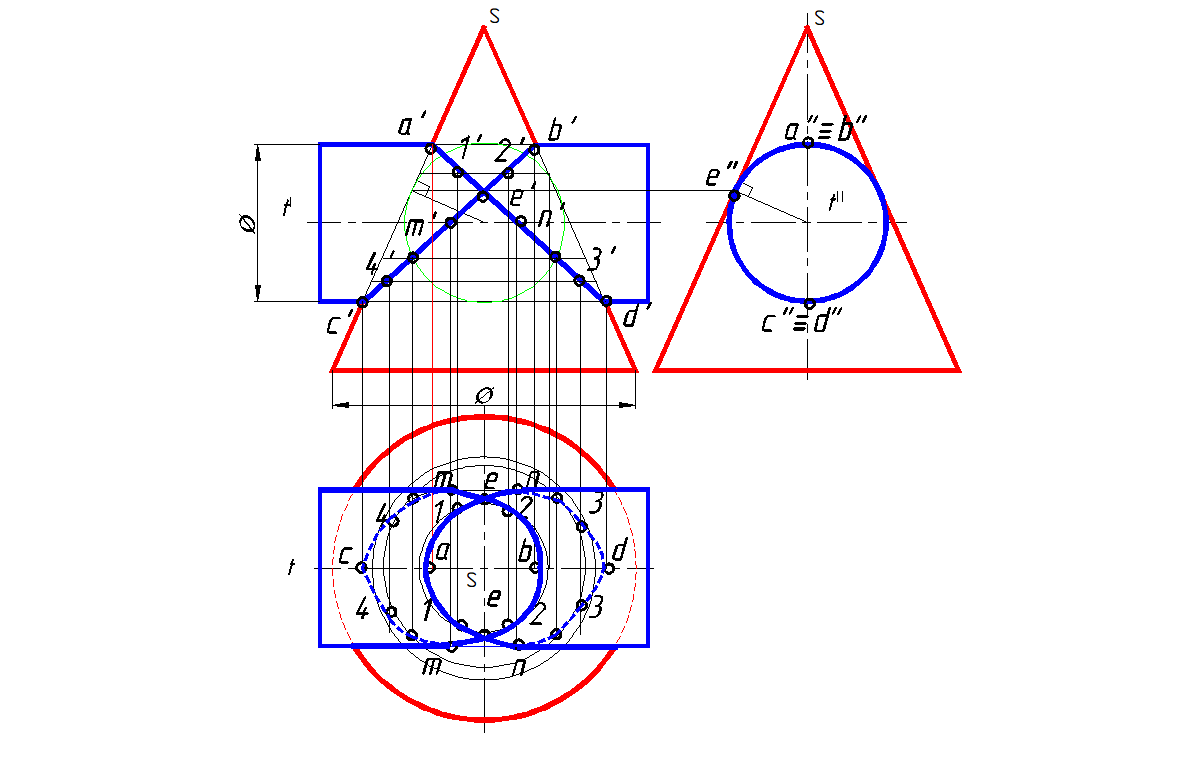
Рис. 166. Поверхности, описанные вокруг одной сферы. Построение

линии пересечения поверхностей

 

 

5. Развертки кривых поверхностей

Понятие развертки

Если поверхность рассматривать как тонкую, нерастяжимую пленку, то некоторые поверхности путем изгибания могут быть совмещены с плоскостью. Такой процесс совмещения поверхности с плоскостью называется развертыванием поверхности. Поверхность, которая может быть совмещена с плоскостью без разрывов и складок, называется развертывающейся, а полученная при этом плоская фигура – ее разверткой.

Построение разверток многогранных поверхностей рассматривалось в предыдущей лекции. Такие развертки называются точными.

К развертывающимся кривым поверхностям относятся только линейчатые поверхности с пересекающимися смежными образующими: конические, цилиндрические и поверхности с ребром возврата. Развертки таких поверхностей называют приближенными. Развертки неразвертывающихся поверхностей (сфера, тор и т. д.) являются условными.

 

Основные свойства развертки

Поверхность и ее развертку можно рассматривать как точечные множества, между которыми установлено взаимно однозначное соответствие. Отсюда можно отметить основные свойства развертки:

 

1) длины соответствующих линий на поверхности и на развертке равны между собой;

2) прямой линии на поверхности соответствует прямая линия на развертке;

3) угол между линиями на поверхности равен углу между соответствующими линиями на развертке;

4) параллельным прямым линиям на поверхности соответствуют параллельные прямые линии на развертке;

5) площадь, ограниченная линией на поверхности, равна площади, ограниченной соответствующей ей линией, на развертке.

 

Чтобы на развертке построить какую-либо точку, принадлежащую развертываемой поверхности, необходимо предварительно через заданную точку на поверхности провести линию. Затем эту линию нанести на развертку, и на ней отметить точку.

 

 

Конических поверхностей

Развертка поверхности кругового цилиндра и конуса известны из школьного курса. Развертка поверхности кругового цилиндра (рис.167) представляет прямоугольник, одна сторона которого равна высоте цилиндра Н, а другая – длине окружности основания цилиндра

l =2πR,

 

где R – радиус окружности основания цилиндра.

Положение точки А на развертке цилиндрической поверхности найдено с помощью образующей, проходящей через нее. Отрезок прямой А1 на развертке равен длине дуги а1 окружности основания цилиндра, т. е.

l ₁ = 2πR φ^о / 360^о.

 

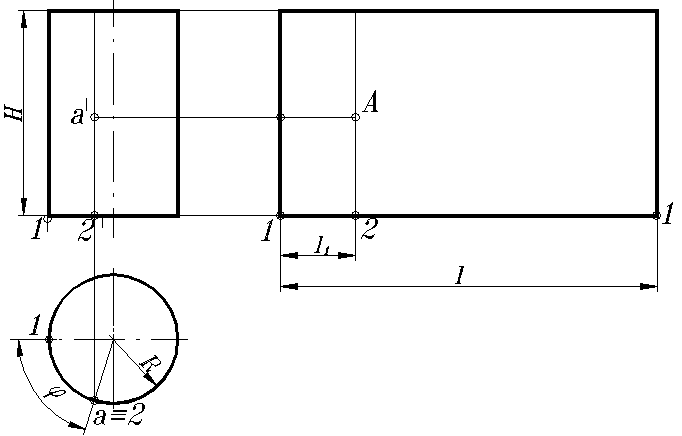
Рис. 167. Развертка поверхности прямого кругового цилиндра

 

Развертка поверхности кругового конуса (рис.168) представляет круговой сектор, радиус которого равен длине образующей конуса, а угол при вершине равен

a^о = 360^о R / L ,

где R – радиус окружности основания конуса;

L – длина образующей этого конуса (рис. 24).

Положение точки А на развертке конуса найдено с помощью образующей S 2, проведенной через нее на поверхности конуса. Угол a₁ на развертке определяется по формуле

 

a^о₁ = a^о φ^о / 360^о.

 

Натуральная величина отрезка образующей SA определена вращением его вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

 

 

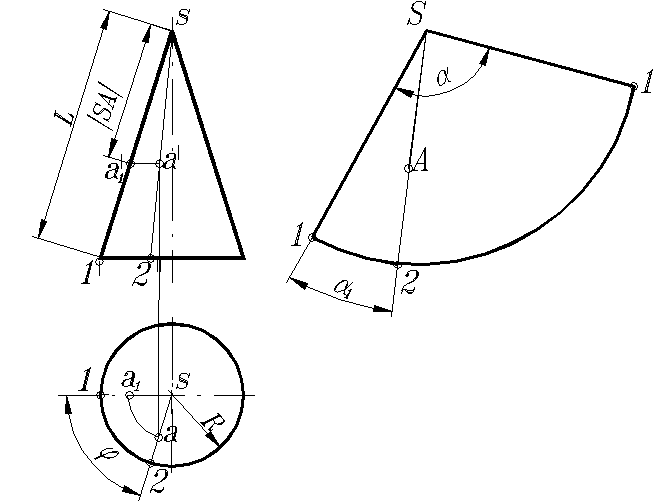
Рис. 168. Развертка поверхности прямого кругового конуса

 

Но такие способы построения разверток ограничены.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Белякова, Е. И . Начертательная геометрия : учеб. пособие для вузов / Е. И. Белякова, П. В. Зеленый ; под ред. П. В. Зеленого. – 3-е изд., испр. – Минск : Новое знание ; М. : ИНФРА-М, 2012. – 265 с. : ил.

2. Белякова, Е. И. Начертательная геометрия. Практикум : учеб. пособие для вузов / Е. И. Белякова, П. В. Зеленый ; под ред. П. В. Зеленого. – 2-е изд., испр. – Минск : Новое знание ; М. : ИНФРА-М, 2012. – 214 с.

3. Нартова, Л. Г. Начертательная геометрия : учеб. для вузов / Л. Г. Нартова, В. И. Якунин. – 3-е изд., стер. – М. : Академия, 2011. – 192 с. : ил.

4. Общие правила выполнения чертежей : ГОСТ 2.301–68… ГОСТ 2.321–84. – М. : Изд-во стандартов, 2004. – 160 с.

5. Чекмарев, А. А . Начертательная геометрия и черчение : учеб. для бакалавров / А. А. Чекмарев. – 4-е изд., испр. и доп. – М. : Юрайт, 2012. – 471 с.

6. Чекмарев, А. А. Начертательная геометрия и черчение : учеб. для вузов / А. А. Чекмарев. – 2-е изд., перераб. и доп. – М. : ВЛАДОС, 2005. – 472 с.

 

Учебное-методическое издание

 

Часть 1

Краткий курс лекций

 

 

Автор-составитель

Аляутдинова Людмила Егоровна

 

 

Ресурсный информационно-образовательный центр

Федеральное государственное автономное образовательное учреждение высшего образования

«Уральский федеральный университет

имени первого Президента России Б.Н.Ельцина»

Нижнетагильский технологический институт (филиал)