Задача. Установлено, что в процессе разрушения горных пород выделяется очень большое количество тепла, которое приводит к нагреву долот до 600 – 1000 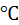 и промывочной жидкости в призабойной зоне пласта. Установить закономерности распределения температуры по глубине скважин и во времени в зависимости от количества тепла, выделяемого в зонах разрушения в единице объема и времени.
и промывочной жидкости в призабойной зоне пласта. Установить закономерности распределения температуры по глубине скважин и во времени в зависимости от количества тепла, выделяемого в зонах разрушения в единице объема и времени.
Дано. Скважина в виде цилиндра заполнена жидкостью, на нижние стенки (торец) действует поток тепла постоянной мощности.
Найти зависимость температуры от глубины скважины и времени T(x,t)
Можно получить уравнение теплопроводности:
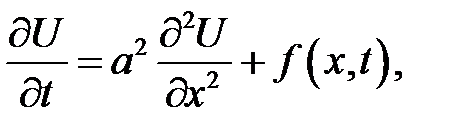 (34.1)
(34.1)
с граничными и начальными условиями:
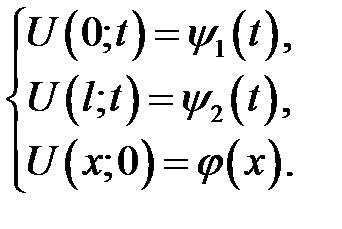
Решение: можно получить уравнение теплопроводности
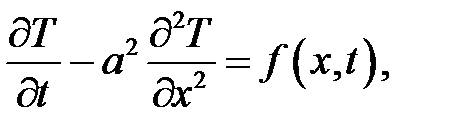
где 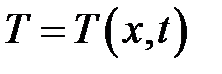 - температура, функция координат, времени;
- температура, функция координат, времени;
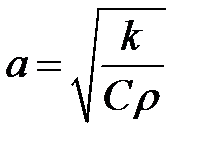 ,
, 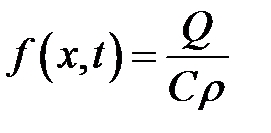 ;
;
k – коэффициент теплопроводности (температуропроводности) глинистого раствора;
С – удельная теплоемкость раствора;
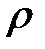 – объемная плотность раствора;
– объемная плотность раствора;
Q – количество тепла, выделенного в единице объема и времени (плотность тепловых источников).
Определим начальное и граничные условия:
граничные условия: 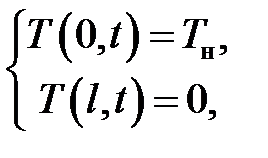
начальное условие: 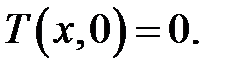
где 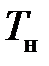 – температура нагрева жидкости на забое за счет выделения тепла;
– температура нагрева жидкости на забое за счет выделения тепла;
l – расстояние вдоль скважины, где нагрев жидкости прекра-щается.
Температуру будем искать в виде:
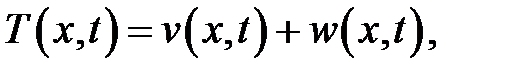
где 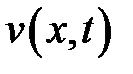 удовлетворяет
удовлетворяет 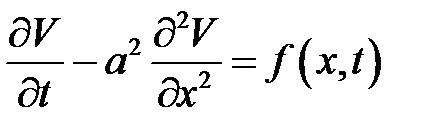 (1) при
(1) при 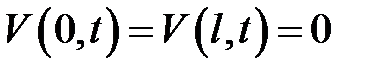 ,
, 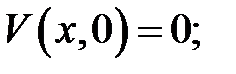
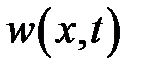 удовлетворяет
удовлетворяет 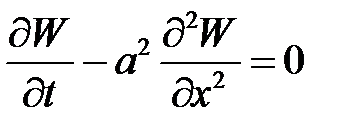 ,
, 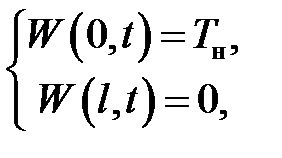
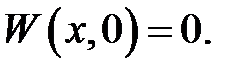
Решим (34.1).
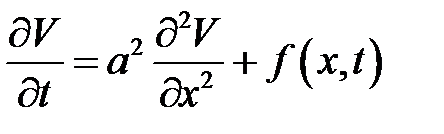 (1)
(1)
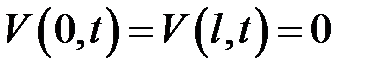 (2)
(2)
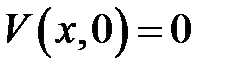 (3)
(3)
 (4)
(4)
— решение уравнения (1).
Разложение по синусам возможно, т.к. х > 0. Найдем 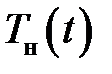 .
.
Условие (2) выполняется автоматически. Пусть функция 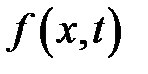 разложима в ряд Фурье:
разложима в ряд Фурье:
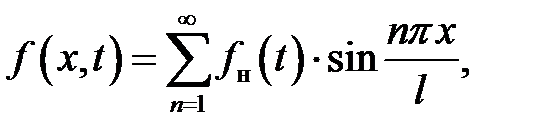 (5)
(5)
где 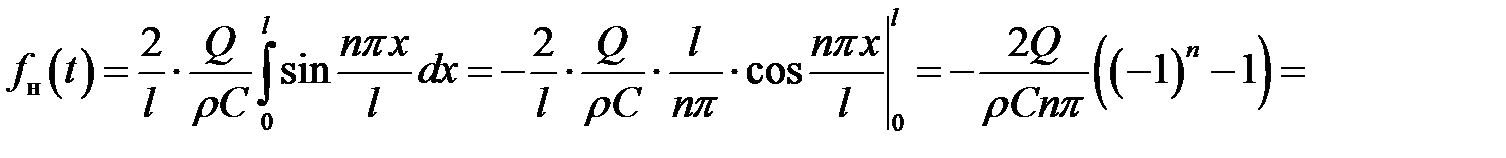
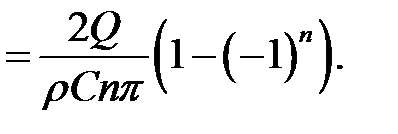
Функция 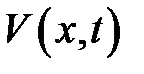 равенства (4) является решением (1) → удов-леворяет (1):
равенства (4) является решением (1) → удов-леворяет (1):
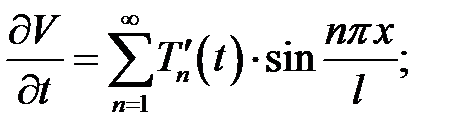
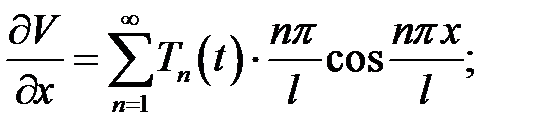
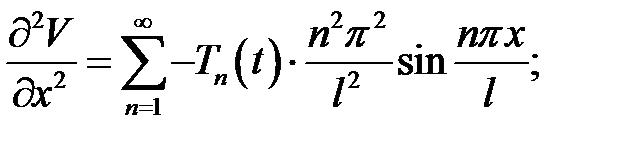
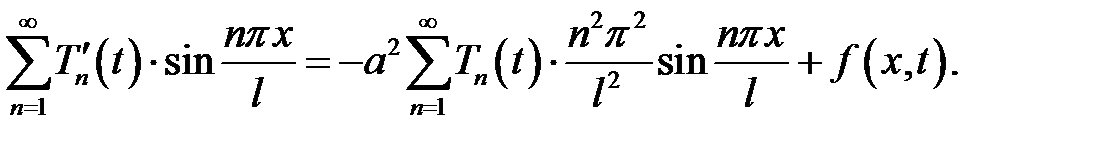
Вместо  подставим его выражение (5):
подставим его выражение (5):
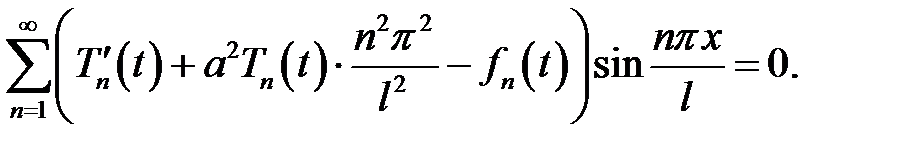
Отсюда необходимо выполнения условия:
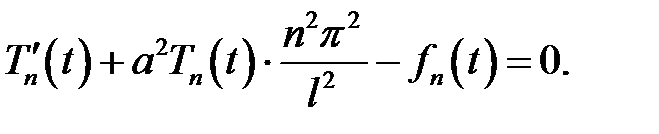
Обозначим  , получим
, получим 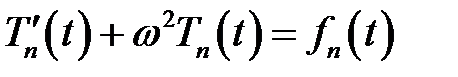 – линейное дифференциальное уравнение первого порядка:
– линейное дифференциальное уравнение первого порядка:
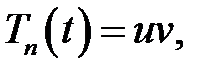
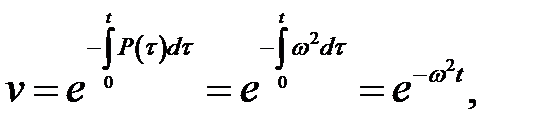 (6)
(6)
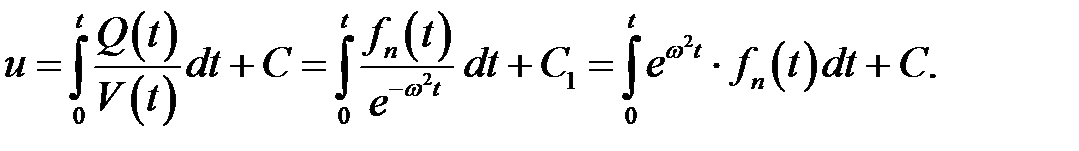
Для определения С воспользуемся уравнением (3):
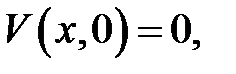
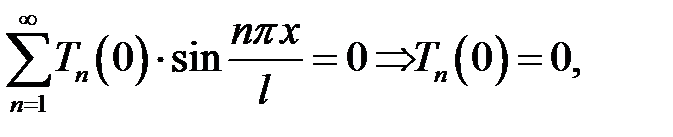
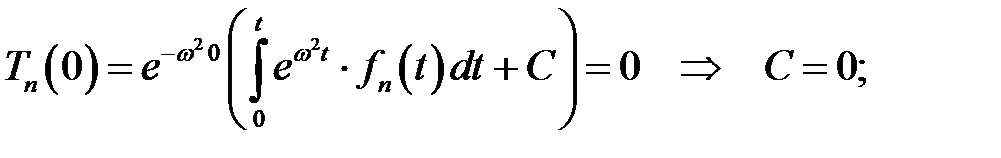
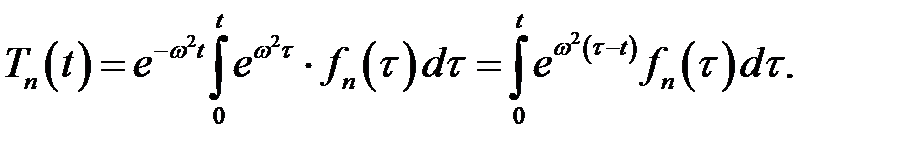
Подставив вместо 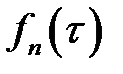 его выражения, получим:
его выражения, получим:
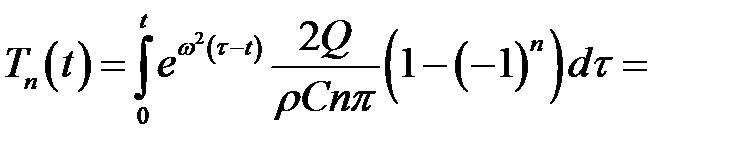
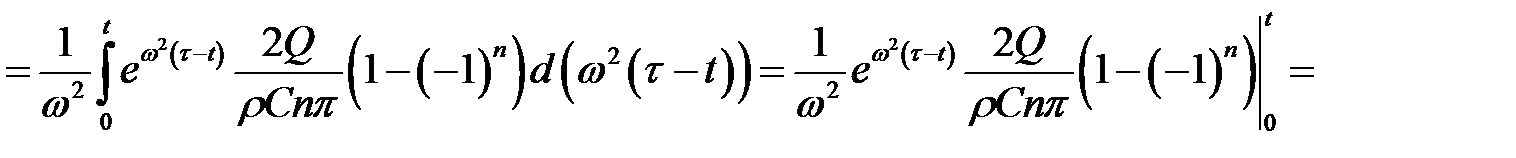
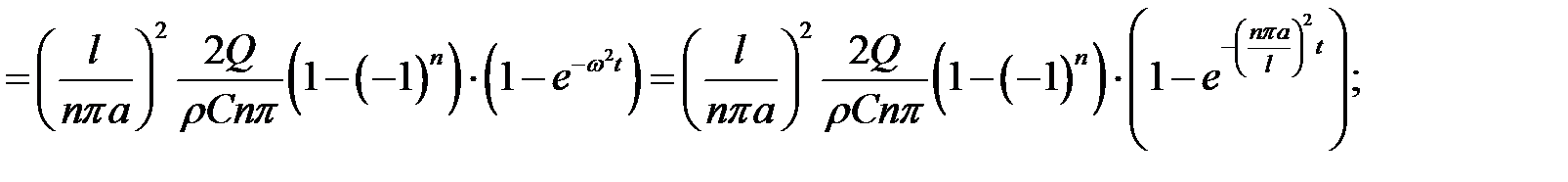
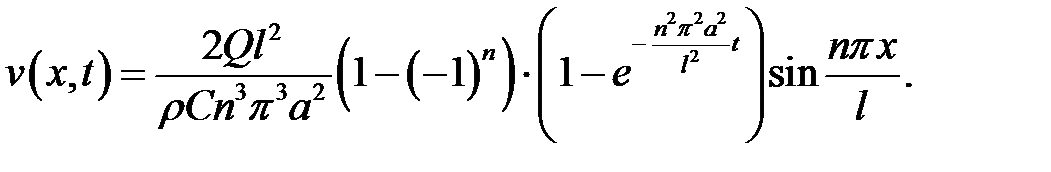 (7) Определим
(7) Определим 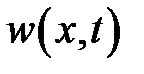 . Решим уравнение
. Решим уравнение 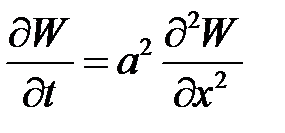 с граничными условиями
с граничными условиями 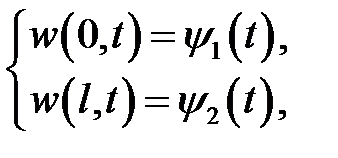 и начальным условием
и начальным условием 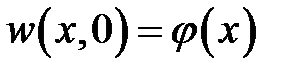 .
.
Решение будем искать в виде:
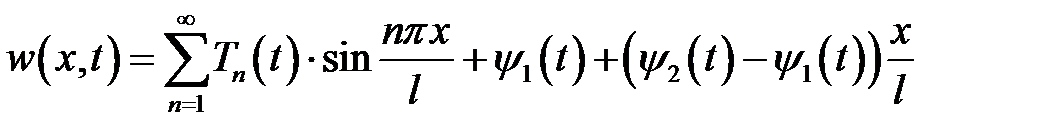 ,
,
Котороеудовлетворяет граничным условиям.
Тогда 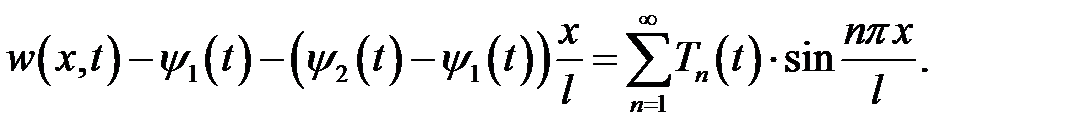 (8)
(8)
По формулам разложения в ряд Фурье:
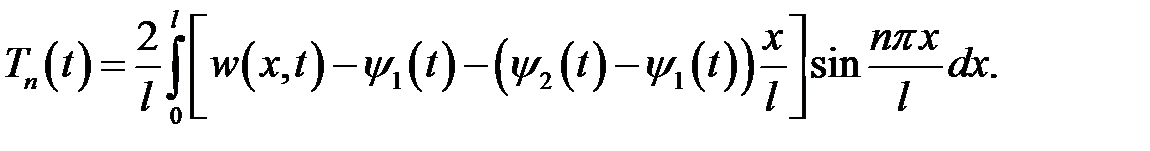 (9)
(9)
Правую часть выражения (9) проинтегрируем по частям, т.е.
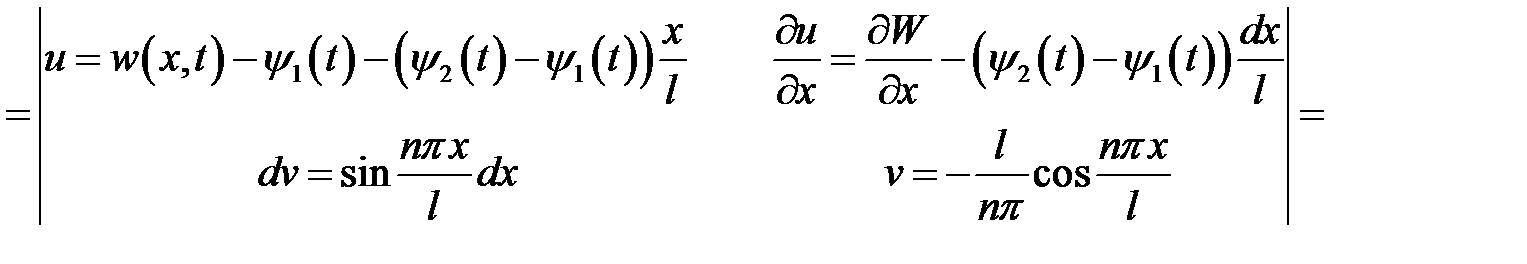

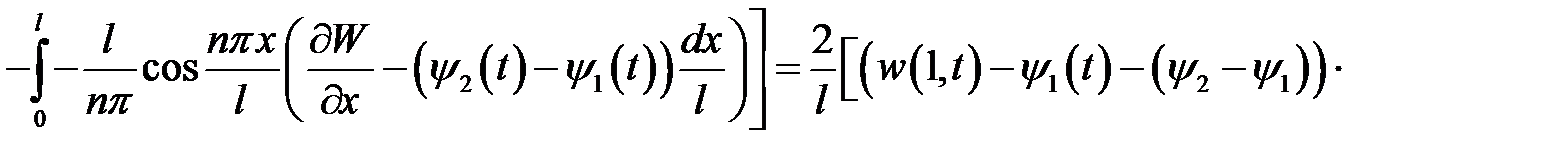
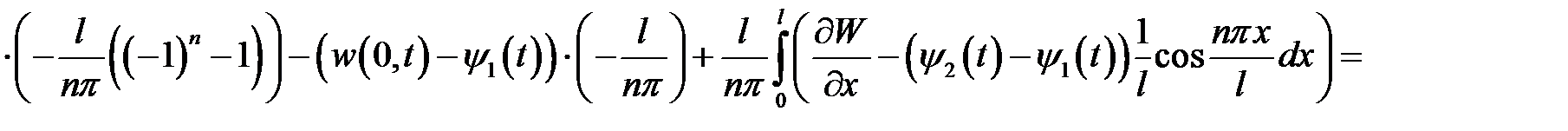
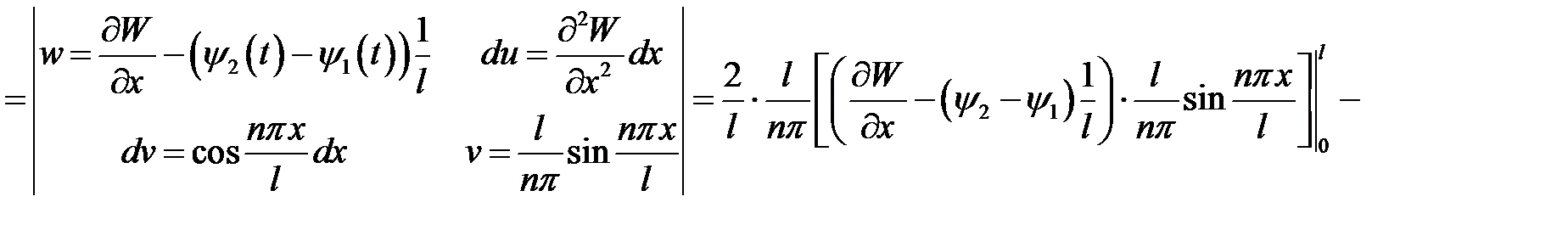
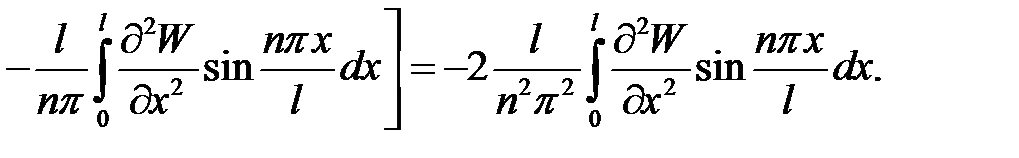
Значит, 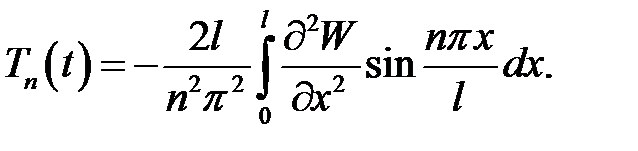
Из (7) → 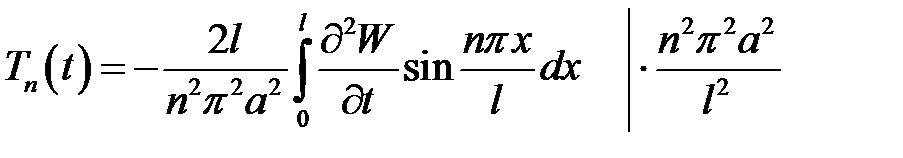
Выражение (8) продифференцируем по t :
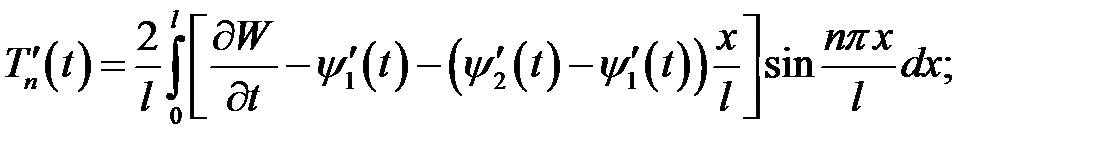
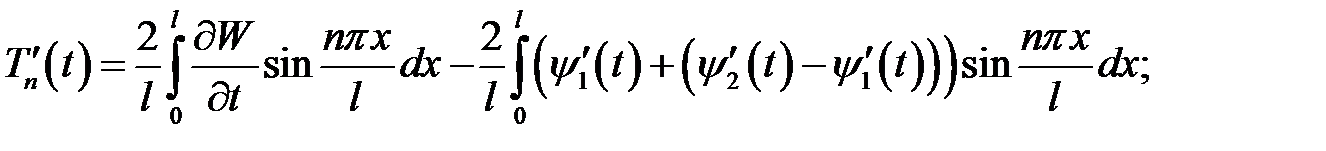
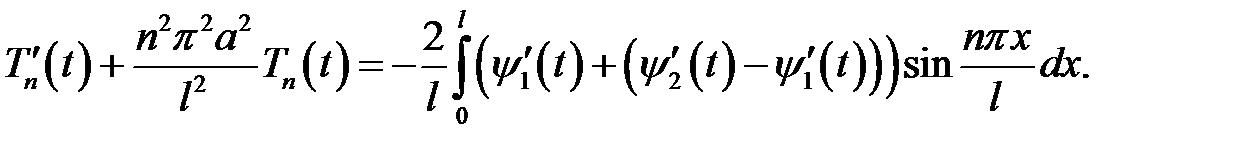
В нашем случае 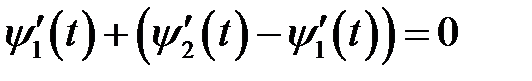 , тогда
, тогда
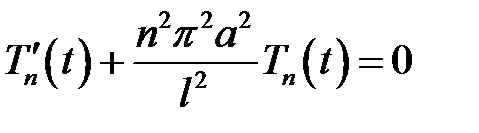 ;
;
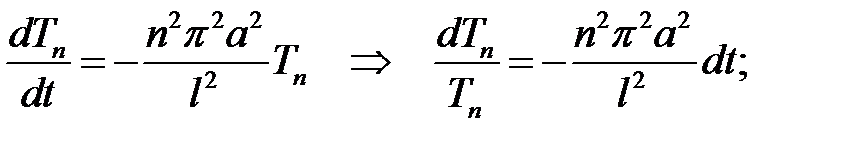
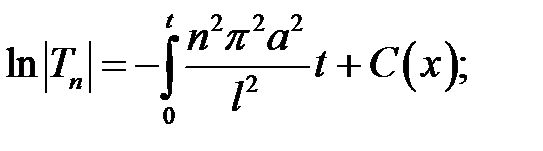
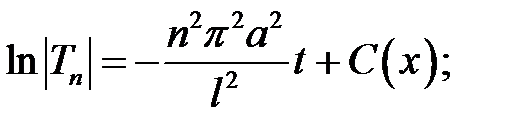
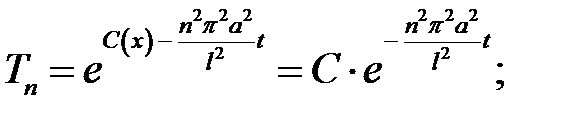
где, очевидно 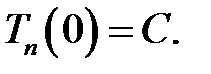
Воспользуемся начальным условием 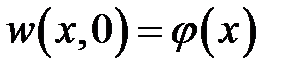 и выражением (8):
и выражением (8):

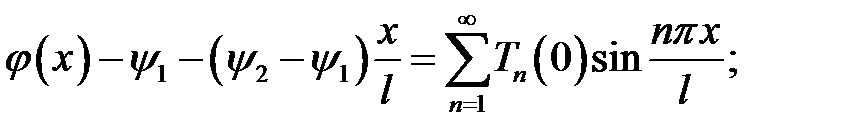
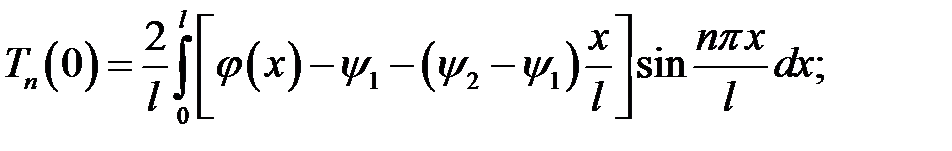
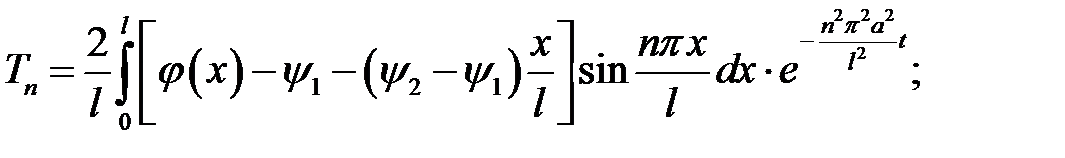
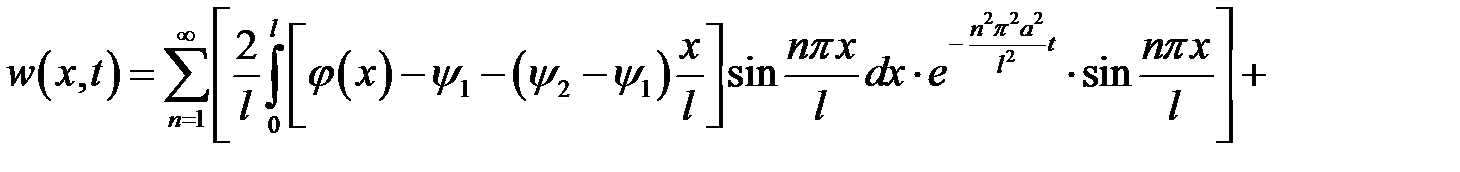
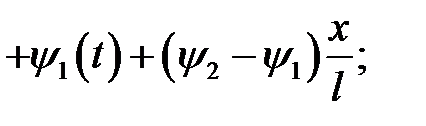
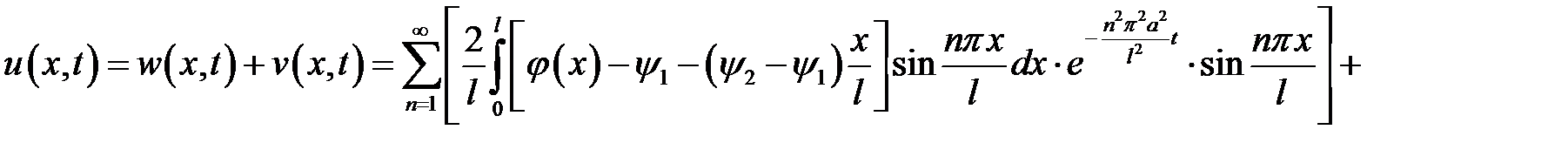
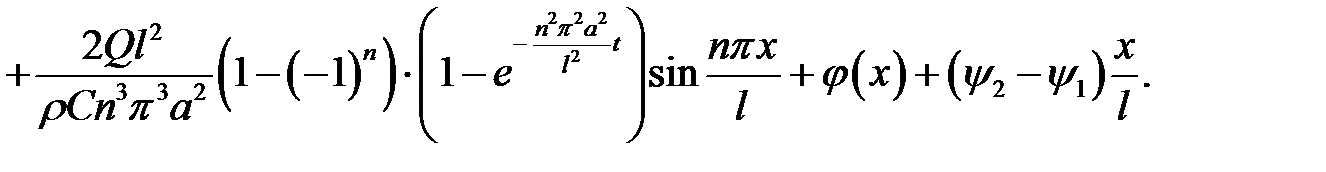
Представим скважину в виде однородного стержня, теплоизо-лированного со всех сторон, кроме нижнего конца, и достаточно тонкого, чтобы считать температуру на всей площади поперечного сечения одинаковой, с граничными и начальными условиями:
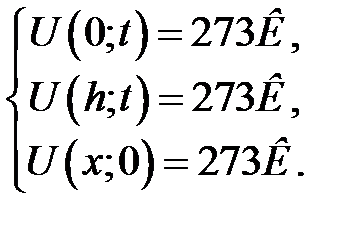
Если стержень нагрет неравномерно, то в нем будет происхо-дить перенос тепловой энергии, и температура в сечениях будет меняться.
В дополнение к этому предположим, что внутри стержня поро-ждается или поглощается тепло вследствие, например, химических реакций. Получим функцию Q – количество тепла, выделяемое единицей объема за единицу времени. Назовем ее плотностью тепловых источников. Вычисляя в системе Mathematica, можем узнать температуру жидкости в призабойной зоне скважины в зависимости от глубины скважины (рис. 33.1).
При консультации с преподавателями специальных дисциплин студенты получили сведения, о том, что нагрев жидкости практи-чески прекращается на глубине примерно равной 2/3 от поверхности земли. Рассматривая скважину глубиной 2500 метров, используя полученные результаты для нахождения температуры промывочной жидкости, определили, что теория не противоречит практике, более того, позволяет более точно вычислять температуру нагрева в любой точке скважины.
Рассмотрение подобных задач является убедительным доказа-тельством для студентов того, что моделирование позволяет пред-сказать ситуацию, имитировать особенности функционирования сис-темы, уменьшает потребности в сложном оборудовании и сложных лабораторных испытаниях, позволяет сократить сроки исследования.

Рис. 34.1. Пример вычисления температуры промывочной жидкости и бурильного инструмента за счет трения при бурении
Дата: 2018-09-13, просмотров: 945.