Для уравнения теплопроводности
Если к уравнению (25.1) добавить одно начальное условие и два граничных, то задача будет иметь единственное решение. Начальное условие:

означает, что при t = 0 температура во всех точках стержня задается функцией  . Если стержень конечен и располагается на участке (О, l) оси Ох, то граничные условия задаются на концах стержня х = 0, х = l, которые могут контактировать с окружающей средой. Когда на поверхности контакта температура стержня U и окружающей среды
. Если стержень конечен и располагается на участке (О, l) оси Ох, то граничные условия задаются на концах стержня х = 0, х = l, которые могут контактировать с окружающей средой. Когда на поверхности контакта температура стержня U и окружающей среды  одинакова, теплообмен между ними исключен. Эксперименты показывают, что при
одинакова, теплообмен между ними исключен. Эксперименты показывают, что при  за время dt через малую поверхность контакта S из стержня в окружающую среду проходит количество тепла:
за время dt через малую поверхность контакта S из стержня в окружающую среду проходит количество тепла:
 (26.1)
(26.1)
где h— коэффициент теплообмена,  . Формулу (26.1) называют законом Ньютона. На разных концах стержня могут быть различные значения h и
. Формулу (26.1) называют законом Ньютона. На разных концах стержня могут быть различные значения h и  , т. к. разные концы стержня могут контактировать с различными внешними средами. Пусть на левом конце эти значения равны
, т. к. разные концы стержня могут контактировать с различными внешними средами. Пусть на левом конце эти значения равны  ,
,  , а на правом —
, а на правом —  ,
,  . На левом конце выходящий из стержня в окружающую среду тепловой поток направлен в отри-цательную сторону, поэтому:
. На левом конце выходящий из стержня в окружающую среду тепловой поток направлен в отри-цательную сторону, поэтому:
 (1)
(1)
(25.3), (1) →  или
или
 (2)
(2)
На правом конце  (3)
(3)
(25.3), (3) →  или
или
 (4)
(4)
Таким образом, мы получили следующие граничные условия:
 (26.2)
(26.2)
где 
 — температуры внешних сред соответственно около левого и правого конца. Перечислим некоторые граничные условия для правого конца.
— температуры внешних сред соответственно около левого и правого конца. Перечислим некоторые граничные условия для правого конца.
а) На конце х = l происходит теплообмен с окружающей сре-дой. В этом случае граничное условие имеет вид:
 .
.
б) На конце х = lподдерживается температура  . Соответ-ствующее граничное условие таково:
. Соответ-ствующее граничное условие таково:

Это равенство можно получить также из условия а), в котором все члены надо разделить на  и положить
и положить  , что соответствует идеальному теплообмену.
, что соответствует идеальному теплообмену.
в) Конец х = l теплоизолирован. Граничное условие запишется в виде:
U x(l, t) = 0.
Оно получается из а) при h l = 0, что означает отсутствие тепло-обмена.
г) Через конец стержня х = l протекает тепловой поток Q(t). Граничное условие имеет вид:

Обоснуем это равенство. По определению тепловым потоком называется величина  — количество тепловой энергии, протекающей через поверхность S за единицу времени.
— количество тепловой энергии, протекающей через поверхность S за единицу времени.
(25.3) →  (5)
(5)
(5) →  (6)
(6)
Введем обозначение:  (7)
(7)
(6),(7) → 
Разделим обе части уравнений (26.2) на k и введем обозначения:
 (26.3)
(26.3)
Получим:


Задача о собственных значениях
Теорема
Уравнение
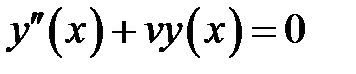 (27.1)
(27.1)
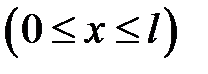
с однородными граничными условиями:
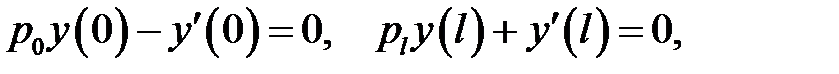 (27.2)
(27.2)
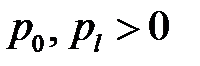 (27.3)
(27.3)
имеет нетривиальное решение только тогда, когда
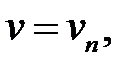 (27.4)
(27.4)
где v n (n = 1, 2, ...) — один из корней уравнения:
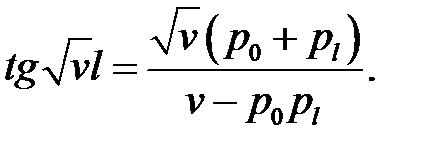 (27.5)
(27.5)
Задача (27.1) — (27.3) имеет следующее решение:
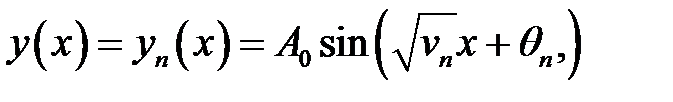 , (27.6)
, (27.6)
где
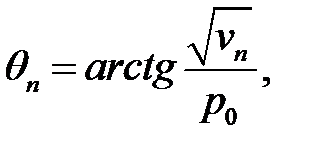 (27.7)
(27.7)
А n— произвольная постоянная.
Доказательство.
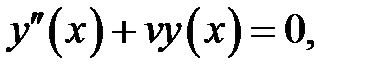 (1)
(1)
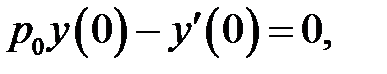 (2)
(2)
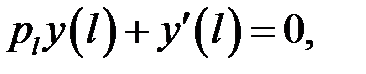 (3)
(3)
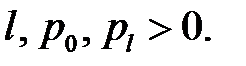 (4)
(4)
Ищем нетривиальное решение, т. е. решение вида:
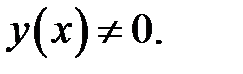 (5)
(5)
Сначала покажем, что решение уравнения (1) возможно только при v > 0, т. е. что случаи v< 0 и v = 0 исключаются.
Предположим, что v< 0. (6)
(6) → можно ввести величину 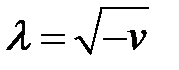 . (7)
. (7)
(7) → 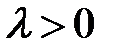 (8)
(8)
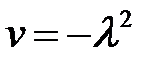 (9)
(9)
(9),(1) → 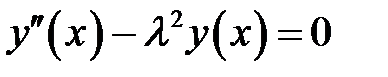 (10)
(10)
(10) → 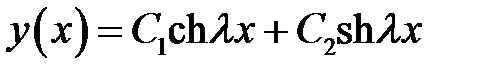 (11)
(11)
(11) → 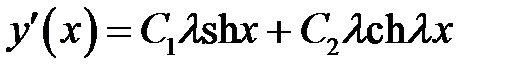 (12)
(12)
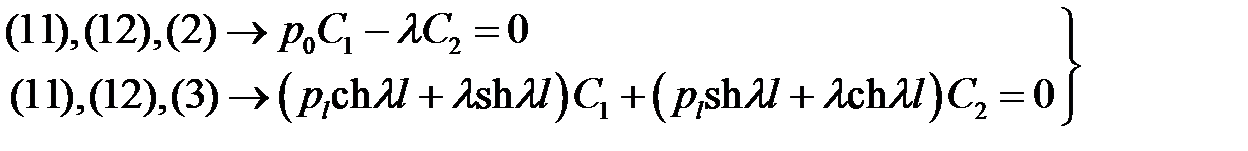 (13)
(13)
Решим эту систему относительно С1 и С2. Для этого вычислим определитель системы:
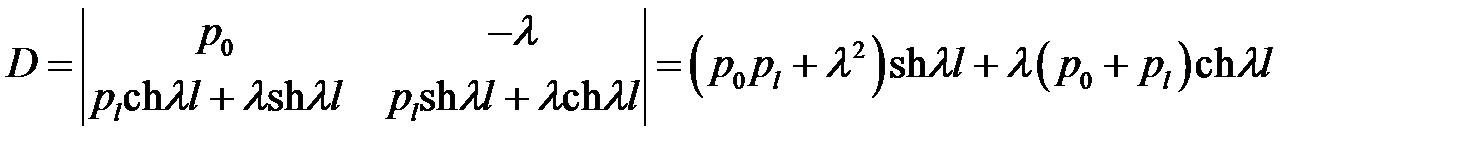 (14)
(14)
(14), (4), (8) →  , т. е.
, т. е. 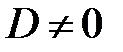 (15)
(15)
(15) → однородная система (13) имеет только тривиальное ре-шение:
С1= 0, С2 = 0. (16)
(16), (11) → 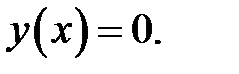
Это противоречит условию (5).
Таким образом, случай (6) отпадает.
Предположим, что v = 0. (17)
(1) → 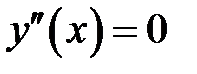 (18)
(18)
(18) → 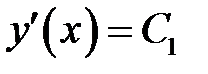 (19)
(19)
(19) → 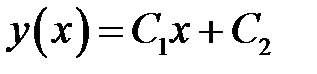 (20)
(20)
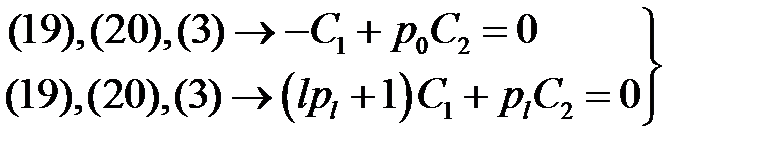 (21)
(21)
Решим эту систему относительно С1, С2. Для этого вычислим определитель:
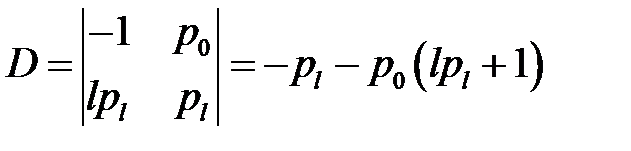 (22)
(22)
(4), (22) → D< 0, т.е. 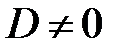 (23)
(23)
(23) → однородная система (21) имеет только тривиальное решение:
С1 = 0, С2 = 0. (24)
(24),(19) → у(х) = 0
Это противоречит условию (5).
Таким образом, случай (17) отпадает.
Вывод: нетривиальное решение уравнения (1) возможно только при v > 0.
Пусть в (1) v> 0 (25)
(25) → можно ввести величину 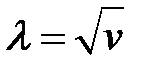 (26)
(26)
(26) → (27)
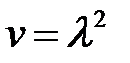 (28)
(28)
(28), (1) → 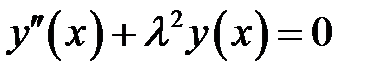 (29)
(29)
(29) → 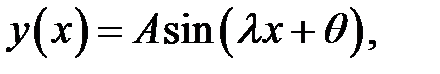 (30)
(30)
где А, 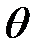 — постоянные интегрирования.
— постоянные интегрирования.
Потребуем, чтобы функция (30) удовлетворяла условиям (2) и (3).
(30) → 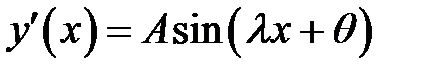 (31)
(31)
(30), (31), (2) → 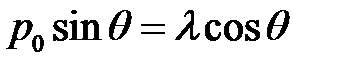
или 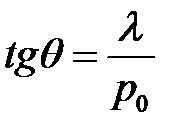 или
или 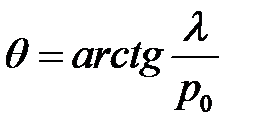 (32)
(32)
(30), (31), (3) → 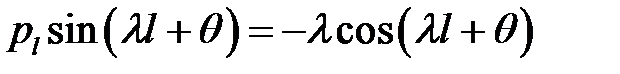
или 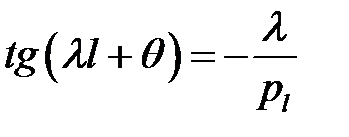 (33)
(33)
или 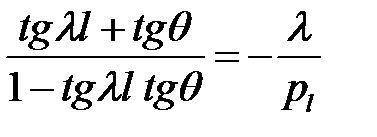 (34)
(34)
(34), (32) → 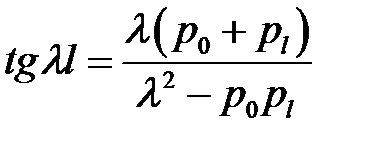 (35)
(35)
(26), (35) → получаем формулу (27.5).
Решим уравнение (35) относительно 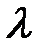 графическим способом. Для этого нарисуем графики левой и правой частей:
графическим способом. Для этого нарисуем графики левой и правой частей:
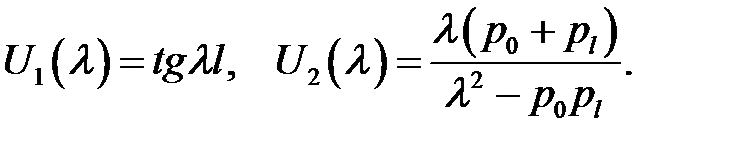
Будем иметь:
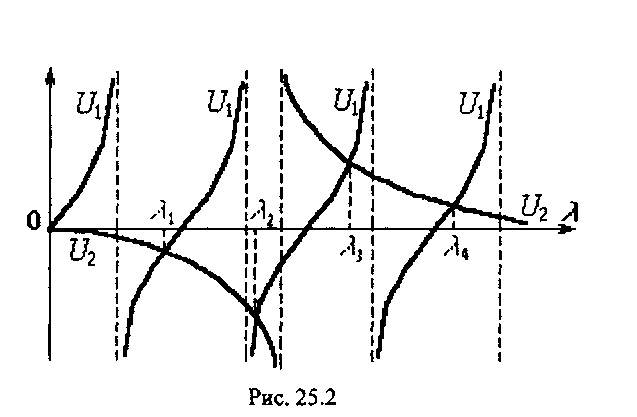
Рис. 25.2
Совпадение графиков, т. е. соблюдение равенства (35), проис-ходит в бесконечном множестве точек пересечения. Абсциссы этих точек дают нам корни уравнения (35):
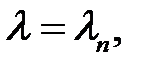 (36)
(36)
где n— номер корня, n =1, 2, ... 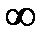 .
.
(36), (26) → 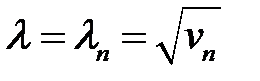 (37)
(37)
(37), (31) → 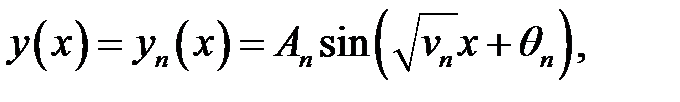
где 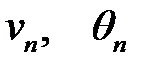 находятся из системы.
находятся из системы.
(32), (37) → 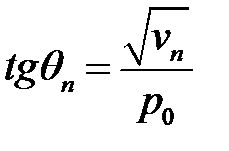 (27.8)
(27.8)
(33), (37) → 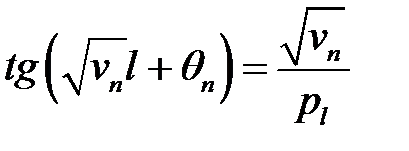 (27.9)
(27.9)
Теорема доказана.
Значения (27.4), при которых уравнение (27.1) имеет нетри-виальные решения, называются собственными значениями, а соответ-ствующие им решения (27.6) — собственными функциями.
Дата: 2018-09-13, просмотров: 962.