В следующих теоремах показывается, как решается волновое уравнение в случае колебаний струны или стержня конечной длины.
Теорема 1
Уравнение
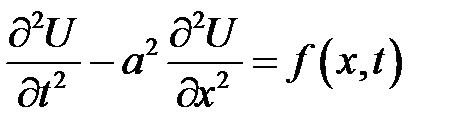 (19.1)
(19.1)
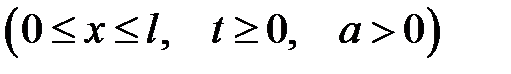
с начальными условиями:
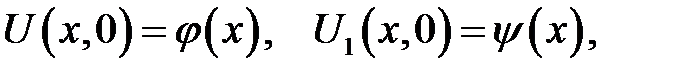 (19.2)
(19.2)
и однородными граничными условиями:
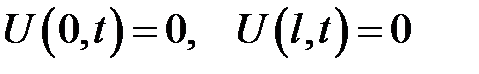 (19.3)
(19.3)
имеет следующее решение:
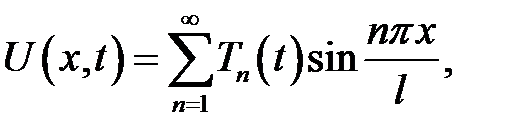 (19.4)
(19.4)
в котором
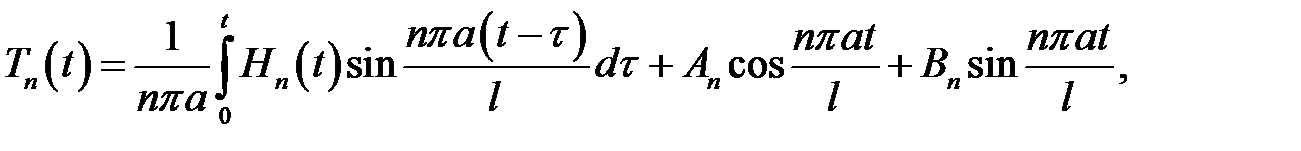 (19.5)
(19.5)
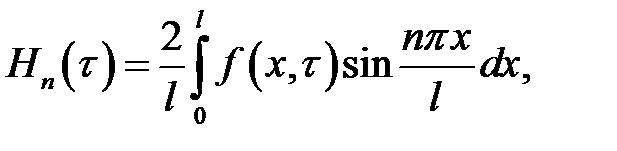 (19.6)
(19.6)
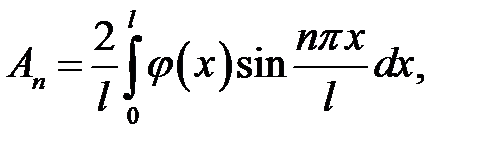 (19.7)
(19.7)
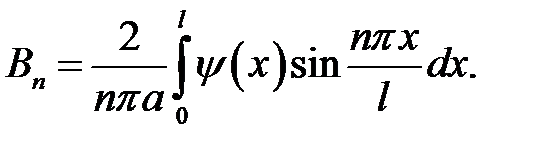 (19.8)
(19.8)
Доказательство.
Дано 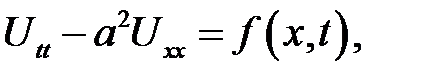 (1)
(1)
где 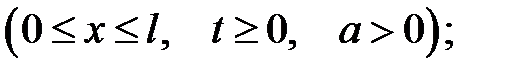
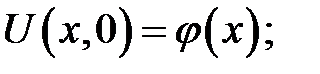 (2)
(2)
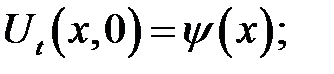 (3)
(3)
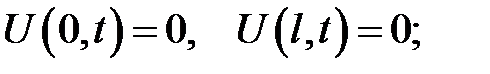 (4)
(4)
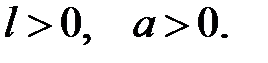 (5)
(5)
Найдем функцию U(x, t), удовлетворяющую условиям (1) — (5). С интервала 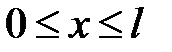 продолжим функции U(x, t), f(x, t) нечетным образом. Как следует из теории рядов Фурье, эти функции можно разложить в ряд по синусам.
продолжим функции U(x, t), f(x, t) нечетным образом. Как следует из теории рядов Фурье, эти функции можно разложить в ряд по синусам.
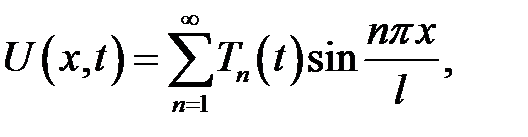 (6)
(6)
Получилась формула (19.4):
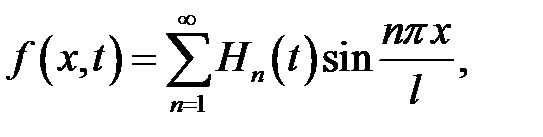 (7)
(7)
(6) → 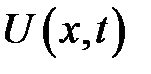 удовлетворяет условиям (4), а также (19.3).
удовлетворяет условиям (4), а также (19.3).
(7) → 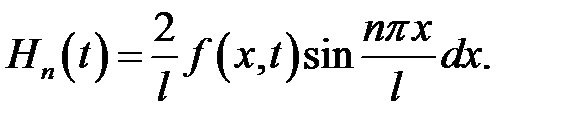
Получилась формула (19.6).
(1), (6), (7) →
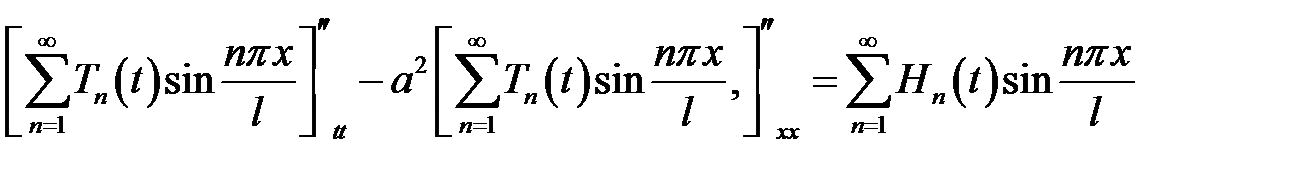
или
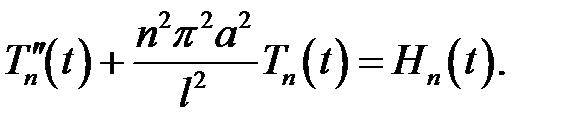 (8)
(8)
Решив это уравнение методом вариации произвольных посто-янных, получим:
(8) → 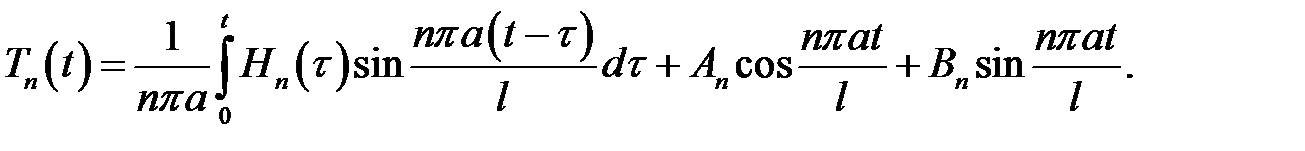 (9)
(9)
Получилась формула (19.5).
Для нахождения 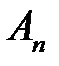 ,
, 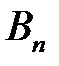 , применим условия (2) и (3).
, применим условия (2) и (3).
(6), (2) → 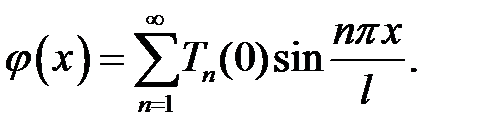 (10)
(10)
(9) → 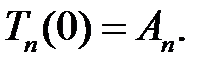 (11)
(11)
(10), (11) → 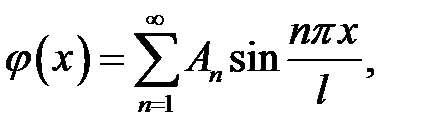 отсюда
отсюда
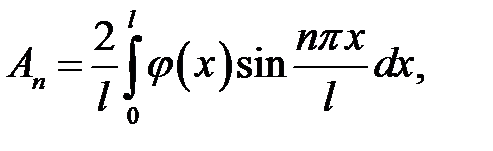 (12)
(12)
Получилась формула (19.7).
(6) → 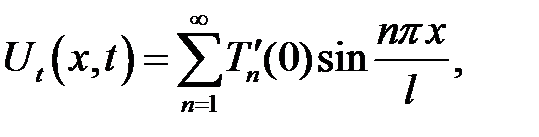 (13)
(13)
(13), (3) → 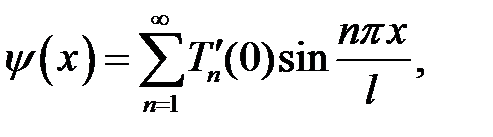 (14)
(14)
(9) → 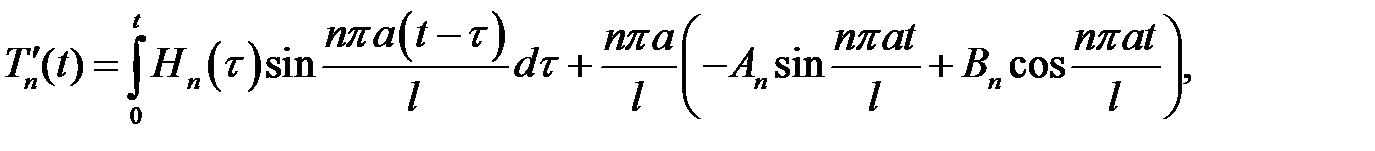 (15)
(15)
(15) → 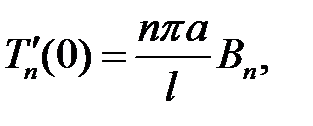 (16)
(16)
(14),(16) → 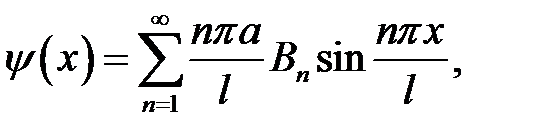 (17)
(17)
(17) → 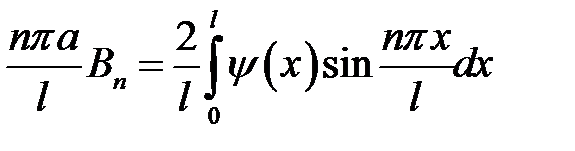 или
или 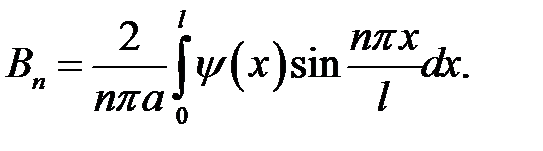
Получилась формула (19.8).
Теорема доказана.
Теорема 2
Уравнение
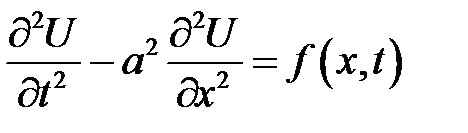 (19.10)
(19.10)
с начальными условиями:
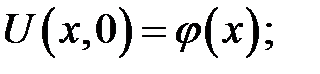
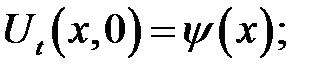 (19.11)
(19.11)
и неоднородными граничными условиями:
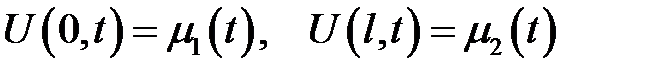 (19.12)
(19.12)
имеет следующее решение:
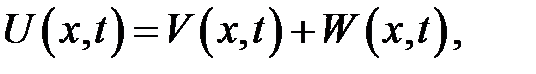
где
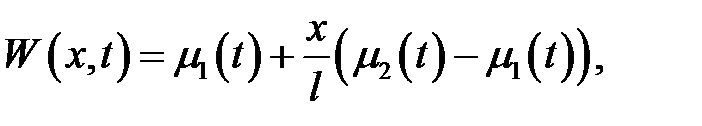
а функция V(x, t) находится из уравнения:
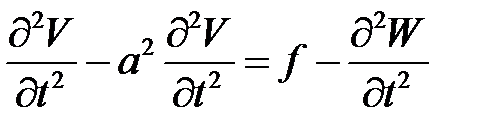
с начальными условиями:
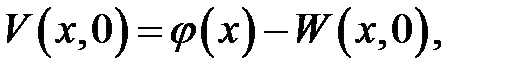
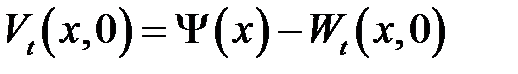
и однородными граничными условиями:
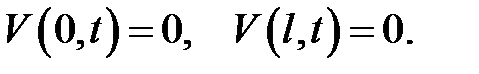
Доказательство.
Даны выражения (19.10) — (19.12).
Будем искать решение уравнения (19.10) в виде:
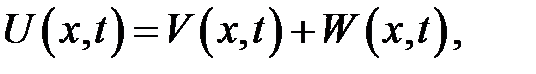 (1)
(1)
где в качестве W возьмем функцию:
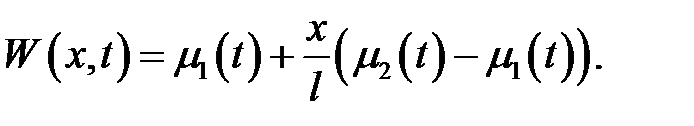 (2)
(2)
(2) → 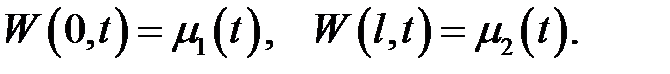 (3)
(3)
(19.10), (1) → 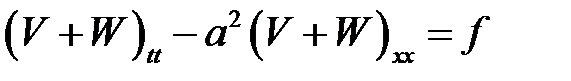
или
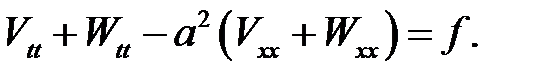 (4)
(4)
(2) → 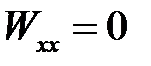
(4) → 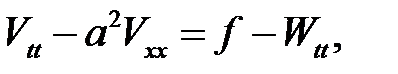
(1) → 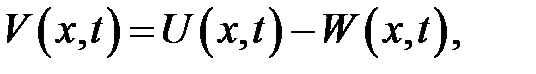 (5)
(5)
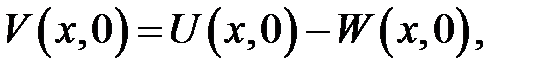
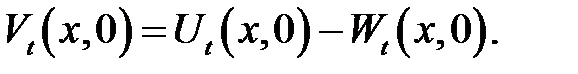
(19.11) → 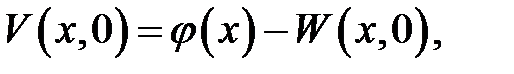
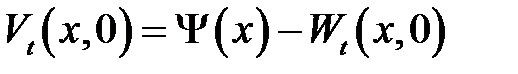 начальные ус-ловия для V(x, t).
начальные ус-ловия для V(x, t).
(5) → 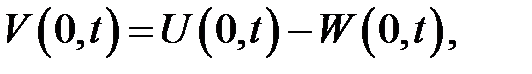
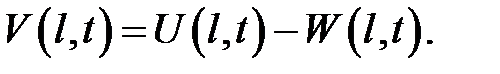
(19.12), (3) → 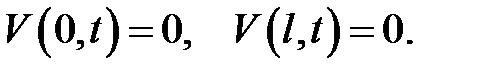
Теорема доказана.
Из теоремы 2 следует, что функция V(x, t) удовлетворяет усло-виям теоремы 1, поэтому V(x, t) находится по формуле (19.4).
Стоячие волны
В теореме 1 пункта 19 приведено решение уравнения колебаний струны длины l с закрепленными концами в виде ряда:
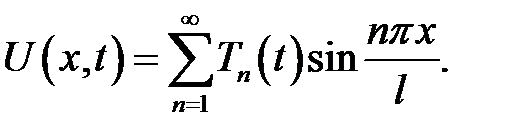 (20.1)
(20.1)
Выясним физический смысл членов ряда (20.1):
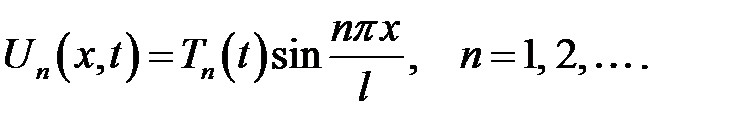 (20.2)
(20.2)
Если зафиксировать время t, то графиком функции U n(x, t) будет синусоида, амплитуда которой равна T n(t). Эта синусоида пересекает интервал 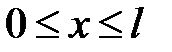 в точках
в точках 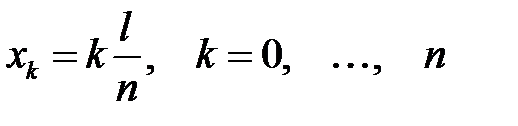 . Как мы видим, х k не зависят от времени. Таким образом с течением времени амплитуда будет меняться, но точки пересечения с осью Ох останутся непо-движными. Это означает, что мы имеем график стоячей волны, назы-ваемой также гармоникой. Ее неподвижные точки называют узлами стоячей волны. Точки, расположенные посередине между узлами, яв-ляются точками экстремума; они называются пучностями стоячей волны. Итак, колебания струны представляют собой сумму или су-перпозицию стоячих волн.
. Как мы видим, х k не зависят от времени. Таким образом с течением времени амплитуда будет меняться, но точки пересечения с осью Ох останутся непо-движными. Это означает, что мы имеем график стоячей волны, назы-ваемой также гармоникой. Ее неподвижные точки называют узлами стоячей волны. Точки, расположенные посередине между узлами, яв-ляются точками экстремума; они называются пучностями стоячей волны. Итак, колебания струны представляют собой сумму или су-перпозицию стоячих волн.
Рассмотрим свободные колебания струны, то есть положим в уравнении
(19.1) 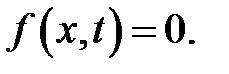 (1)
(1)
По формуле (19.5) найдем амплитуды T n(t), входящие в (20.2).
(1),(19.6) → 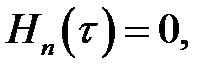 (2)
(2)
(2), (19.5) → 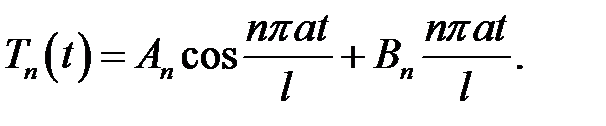 (3)
(3)
Положим 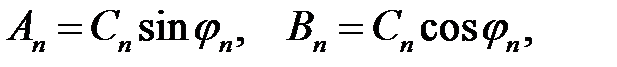 (4)
(4)
(3), (4) → 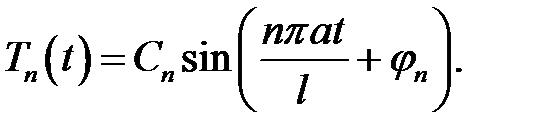 (5)
(5)
(20.2), (5) → 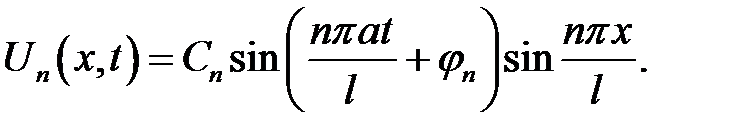 (6)
(6)
Из (6) получаем частоту колебаний n-ой стоячей волны:
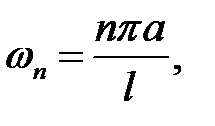 n= 1, 2, 3, … . (20.3)
n= 1, 2, 3, … . (20.3)
Колебания струны мы воспринимаем в виде звука. Каждая сто-ячая волна (20.2) издает звук своей частоты (20.3). Звук, издаваемый стоячей волной, называется простым тоном. Формула (20.1) показы-вает, что звук струны, издаваемый колебанием U(x, t), является нало-жением простых тонов. Можно сказать и так: звук струны разлагается на простые тона. Выделить простые тона можно экспериментально при помощи резонаторов. Повышение частоты колебаний мы вос-принимаем как повышение высоты тона. Тон с самой низкой час-тотой, равной:
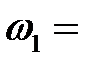 (20.3)
(20.3) 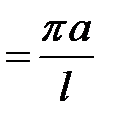
называется основным тоном струны. Так как а = (11.9) 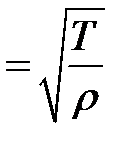 , то:
, то:
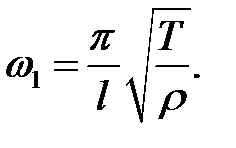
Эта формула показывает, что тон звука тем выше, чем сильнее натяжение и чем короче и легче струна. Тона с более высокими час-тотами 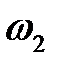 ,
, 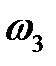 , ... называются обертонами. Они придают окраску, тембр основному тону.
, ... называются обертонами. Они придают окраску, тембр основному тону.
Дата: 2018-09-13, просмотров: 1043.