Если поперечные сечения стержня повернуть вокруг оси на один и тот же угол, то мы получим просто поворот всего стержня как аб-солютно твердого тела. Крутильные колебания были бы невозможны. Поэтому мы будем считать, что во время крутильных колебаний не все сечения поворачиваются на один и тот же угол; кроме того, мы будем предполагать, что

• напряжения, возникающие во время крутильных колебаний, подчиняются закону Гука. Это условие выполняется при небольших углах поворота;

• поперечные сечения во время колебаний остаются плоскими и не смещаются вдоль стержня. Это условие выполняется для круглого стержня, называемого валом.

Направим ось Ох вдоль оси вала. Рассмотрим мысленно некото-рое сечение, перпендикулярное Ох, и через х обозначим абсциссу это-го сечения. Когда вал совершает крутильные колебания, колеблется и это сечение, поворачиваясь то в одну, то в другую сторону вокруг оси Ох. Угол поворота сечения обозначим через .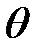

Теорема

Уравнение малых крутильных колебаний однородного вала имеет вид:

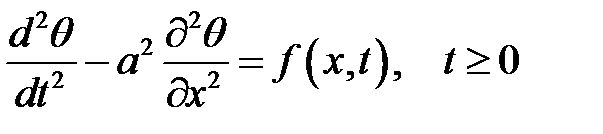                     (23.1)

где 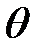 (x, t) — угол поворота в момент времени t поперечного сечения с абсциссой х,

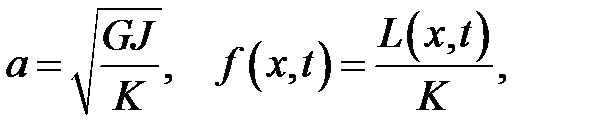
G— модуль сдвига, J— полярный момент инерции поперечного се-чения, К— момент инерции единицы длины стержня, L(x, t) — внешний закручивающий момент, приходящийся на единицу длины.

Доказательство.

Наша цель — для каждого малого элемента (кусочка) вала получить уравнение вращательного движения 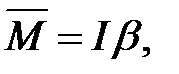         (1)

где М— момент силы, приложенной к этому элементу,

I— момент инерции элемента,

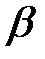— угловое ускорение элемента.

Направим ось Ох вдоль оси вала. Выделим мысленно элемент вала стержня между поперечными сечениями, абсциссы которых х и х + dx. Обозначим эти сечения S(x) и S(x + dx).

Длина этого элемента равна dx (рис. 23.1).                       (2)

Обозначим через К момент инерции единицы длины вала.(3)

Момент инерции выделенного элемента равен:

I = (2), (3) = Kdx.                                                                 (4)

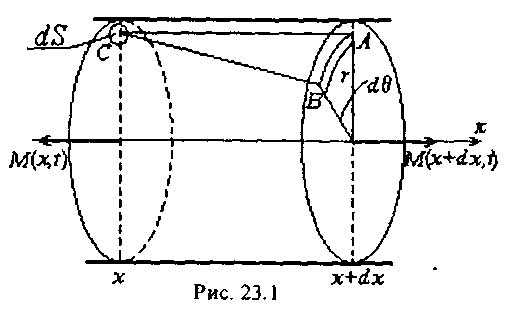
Рис. 23.1

Обозначим через 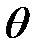 (х, t) угол закручивания в момент t сечения S(x).

Угол поворота всего элемента (с точностью до бесконечно малых первого порядка) равен 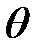 (x, t).                                       (5)

Угловое ускорение выделенного элемента равно:

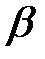 = (5) = 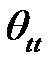.                                                                        (6)

В формуле (1) осталось М— закручивающий момент, вызыва-ющий ускоренное вращение элемента.

Сначала найдем моменты сил, действующих в сечениях S(x) и S(x + dx). Обозначим через dS бесконечно малую площадку в S(x), находящуюся на расстоянии r от оси вращения (рис. 23.1).

В сечении S(x + dx) угол закручивания немного отличается от 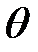 и равен  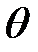+ d .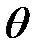

Вследствие дополнительного поворота d 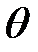 точка А сдвигается на расстояние  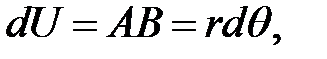                                 (7)

а в сечении S(x) возникает напряжение.

Т. к. 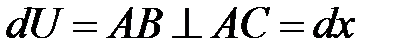, то мы имеем дело с деформацией сдвига:

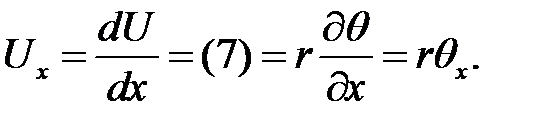                                                     (8)

Этот сдвиг вызывает напряжение на площадке dS, сила которого равна:

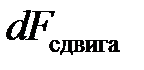= (9.7), (23.2) =  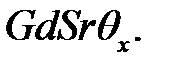                 (23.2)

Момент этой силы:

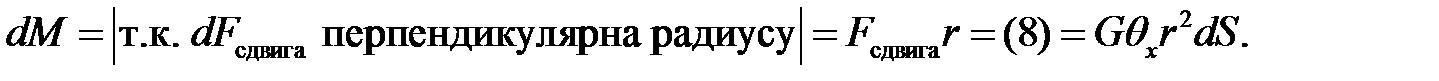(9)

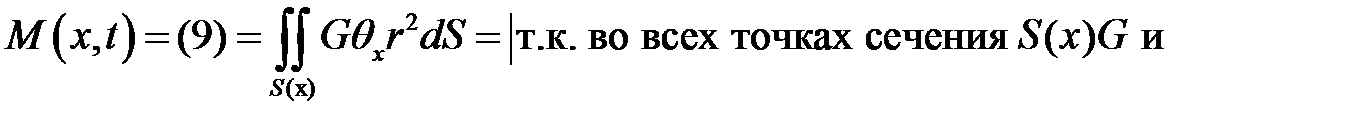
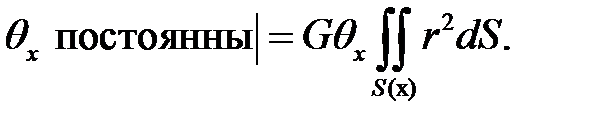                                            (10)

Обозначим 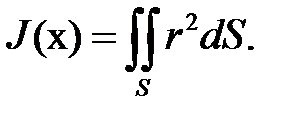— полярный момент инерции сечения S(x).(11)

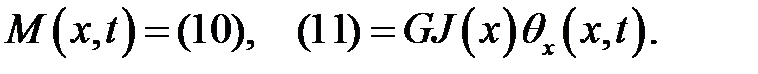              (23.3)

В соседнем сечении S(x + dx) закручивающий момент немного отличается от M(x, t) и равен:

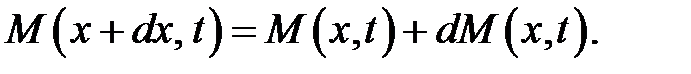                           (12)

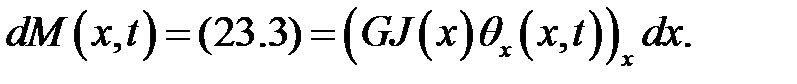                           (13)

Если вал однороден (G = const) и поперечные сечения одина-ковы (J(x) = J = const), то:

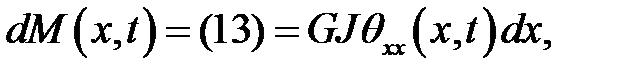                                       (14)

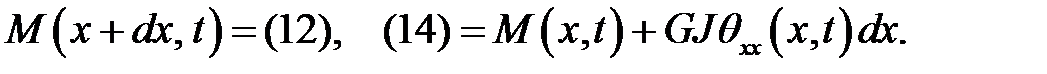               (15)

Пусть кроме этих моментов на вал действует моментвнешних сил, линейная плотность которого L(x, t) (момент на единицу длины).

Спроектируем все моменты на ось Ох (рис.23.1) и найдем сум-марный момент, действующий на наш элемент:

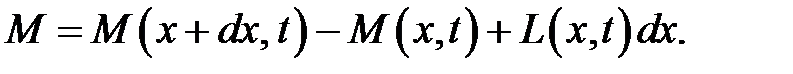                    (16)

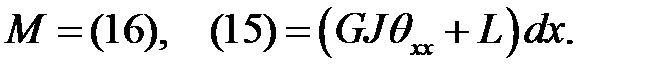                                     (17)

(1), (17), (4), (6) →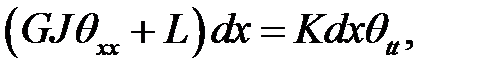  

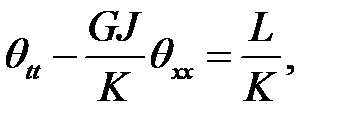                                                             (18)

Введем обозначения 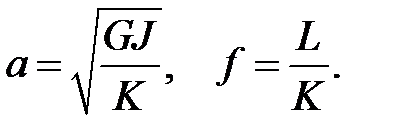                            (19)

(18), (19) →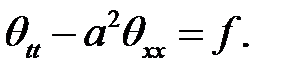

Теорема доказана.