Пусть струна длины l с закрепленными концами (1)
колеблется в вязкой среде. (2)
Требуетcя решить уравнение колебаний (11.1) такой струны при произвольных начальных условиях 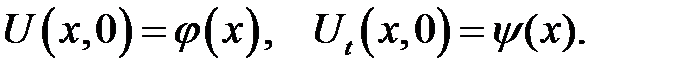
(1) → 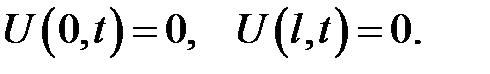
(2) → внешней силой, действующей на струну, оказывается сила сопротивления среды.
Будем считать, что плотность силы сопротивления пропорцио-нальна скорости сечений струны 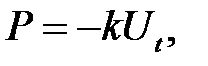 (3)
(3)
где k— коэффициент, пропорциональный вязкости.
(11.2),(3) → 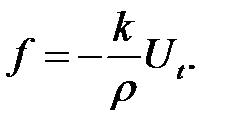 (4)
(4)
Введем обозначение 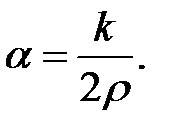 (5)
(5)
(4),(5) → 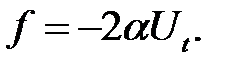 (6)
(6)
(11.1),(6) → 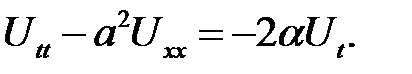
Итак, требуется решить следующую задачу: найти решение ура-внения:
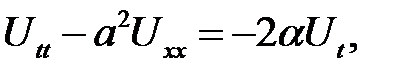 (21.1)
(21.1)
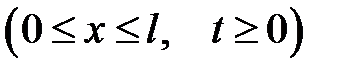
с дополнительными условиями:
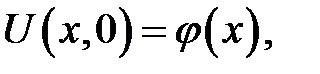 (21.2)
(21.2)
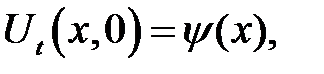 (21.3)
(21.3)
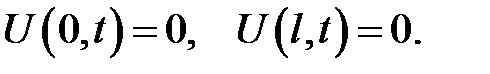 (21.4)
(21.4)
Теорема
Если
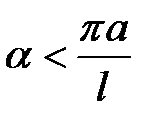 (21.5)
(21.5)
(то есть, при малой вязкости) задача (21.1) — (21.4) имеет следующее решение:
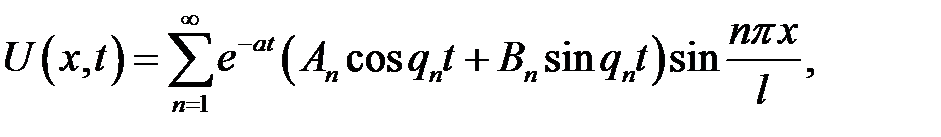 (21.6)
(21.6)
где
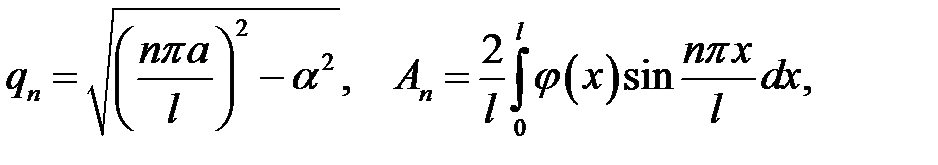 (21.7)
(21.7)
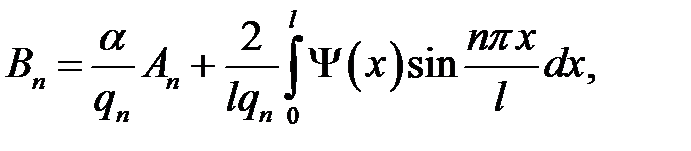 n = 1, 2, … . (21.8)
n = 1, 2, … . (21.8)
Доказательство.
Решение задачи (21.1) — (21.4) будем искать в виде суммы стоя-чих волн:
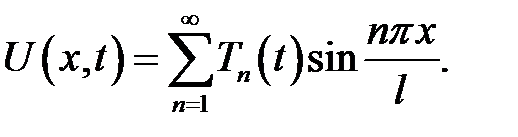 (1)
(1)
где Tn(t) - амплитуда стоячих волн.
(1) →условия (21.4) выполняются.
(21.1),(1) →
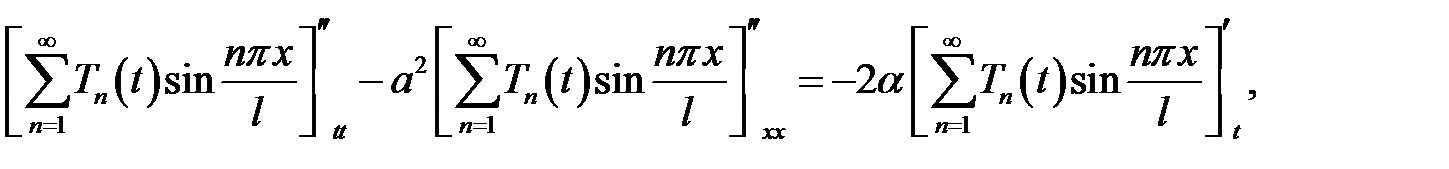
Отсюда 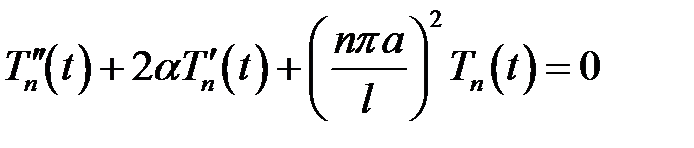 (n = 1, 2, … .) (2)
(n = 1, 2, … .) (2)
Характеристическое уравнение 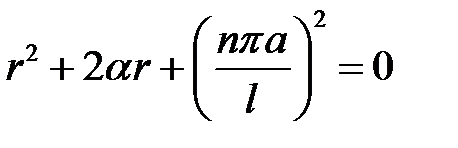
имеет корни 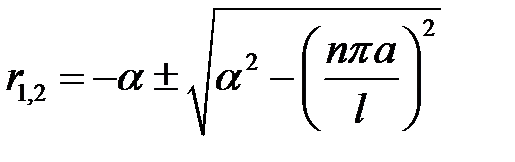 (3)
(3)
(21.5) → 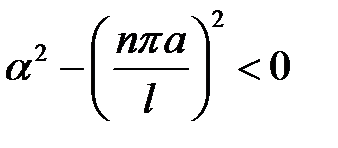 при n =1, 2, ... . (4)
при n =1, 2, ... . (4)
(4) → мы можем ввести обозначение 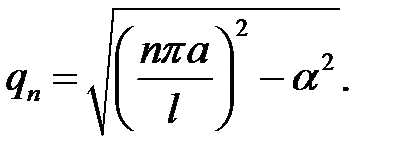 (5)
(5)
(5), (3) → 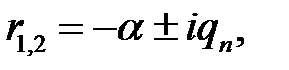 (6)
(6)
(2),(6) → 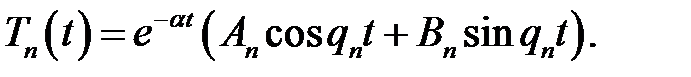 (7)
(7)
При 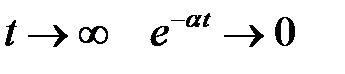 , поэтому Tn(t) → 0. Таким образом, ампли-туды Tn(t) стоячих волн затухают.
, поэтому Tn(t) → 0. Таким образом, ампли-туды Tn(t) стоячих волн затухают.
(1),(7) → 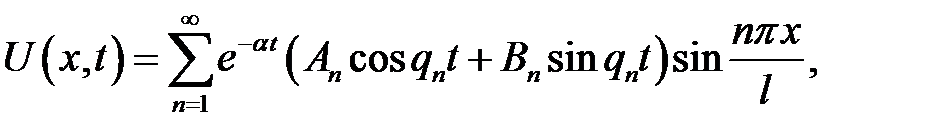 (8)
(8)
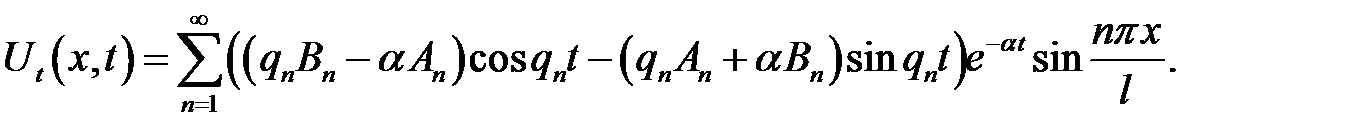 (9)
(9)
(8), (21.2) → 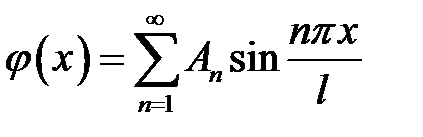 отсюда
отсюда
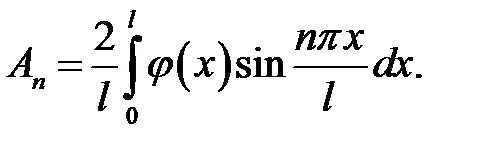
(9), (21.3) → 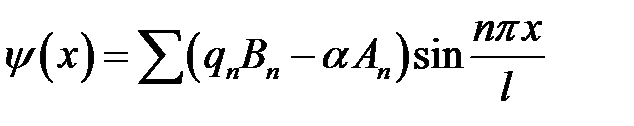 отсюда
отсюда
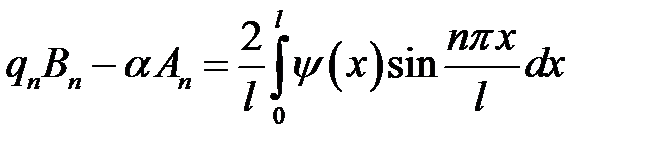
или
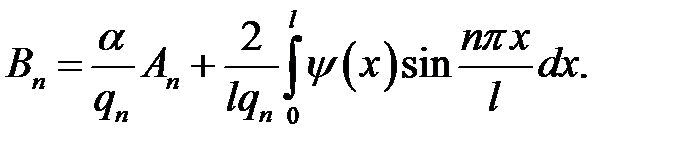
Теорема доказана.
Уравнение продольных колебаний стержня
Если стержень растянуть или сжать вдоль продольной оси, а затем отпустить, то он будет совершать продольные колебания. Мы будем считать, что:
• напряжения, возникающие во время колебаний, подчиняются закону Гука 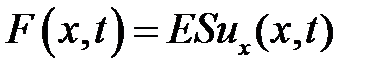 . Это условие выполняется при неболь-ших деформациях;
. Это условие выполняется при неболь-ших деформациях;
• поперечные сечения во время колебаний остаются плоскими и параллельными друг другу. Это условие выполняется, когда попереч-ные размеры стержня невелики по сравнению с его длиной.
Направим ось Ох вдоль стержня. Выделим мысленно некоторое поперечное сечение, то есть сечение, перпендикулярное оси Ох. Пусть, когда стержень в покое и к нему не приложены никакие усилия, это сечение имеет абсциссу х. Можно сказать, что х— это номер или имя, которое мы дали нашему сечению. Когда в стержне происходят продольные колебания, колеблется и это сечение, сме-щаясь с течением времени то в одну, то в другую сторону вдоль оси Ох. Величину смещения обозначим через U.
Теорема
Продольные колебания однородного стержня описываются ура-внением:
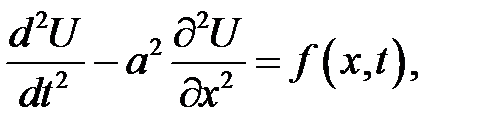 (22.1)
(22.1)
где U(x, t) — продольное смещение в момент времени t поперечного сечения, абсцисса которого была х в состоянии покоя,
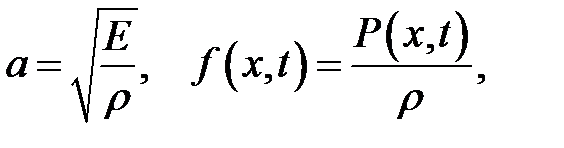 (22.2)
(22.2)
Е— модуль Юнга, 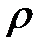 — объемная плотность, Р(х, t) — внешняя сила, приходящаяся на единицу объема и направленная вдоль стержня.
— объемная плотность, Р(х, t) — внешняя сила, приходящаяся на единицу объема и направленная вдоль стержня.
Доказательство.
Наша цель — получить уравнение движения 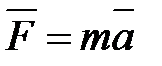 для каждого малого элемента стержня. Выделим мысленно кусочек стержня (х, х + dx), площадь поперечного сечения которого S. Его масса равна
для каждого малого элемента стержня. Выделим мысленно кусочек стержня (х, х + dx), площадь поперечного сечения которого S. Его масса равна
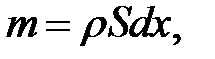 (22.3).
(22.3).
где 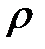 — объемная плотность. Если через U обозначить смещение этого кусочка в направлении оси Ох, то ускорение в этом направ-лении будет равно:
— объемная плотность. Если через U обозначить смещение этого кусочка в направлении оси Ох, то ускорение в этом направ-лении будет равно:
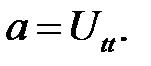 (22.4)
(22.4)
Теперь остается вычислить силу F в х-направлении, которая вызывает ускоренное движение кусочка. Пусть под действием сосед-них участков наш кусочек к моменту времени t удлинился на dU (рис.22.1). По формуле (9.6) продольная сила, действующая в сечении х, равна:
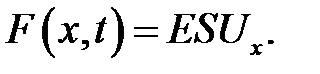 (22.5)
(22.5)
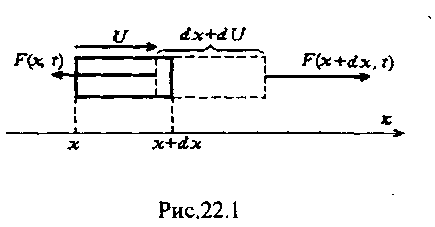
Рис. 22.1
В этот же момент времени в сечении с номером x + dx сила немного отличается от F(x, t) и равна:
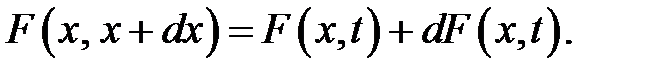
Из (22.5) получаем приращение силы при переходе от сечения х к сечению x + dx, при t = const:
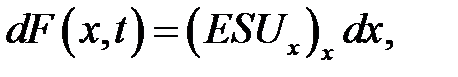
поэтому
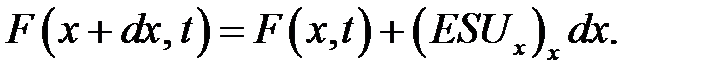 (22.6)
(22.6)
Пусть кроме этих внутренних сил на стержень действует внеш-няя продольная сила с плотностью Р(х, t) (сила на единицу объема). Спроектируем все силы на ось Ох и найдем суммарную силу, дей-ствующую на наш кусочек (рис. 22.1):
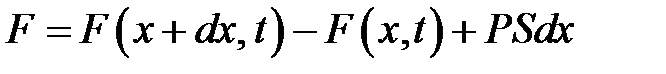
или, если сюда подставить (22.6),
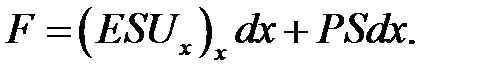 (22.7)
(22.7)
Комбинируя равенства (22.3), (22.4), (22.7), получим:
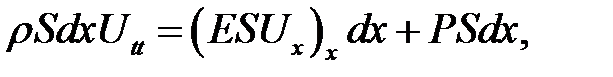
или, после сокращения на 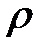 Sdx :
Sdx :
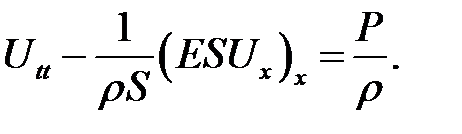
Если E, S одинаковы по всей длине, то:
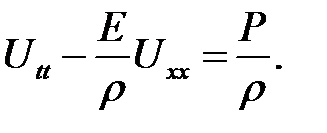
Введя обозначения
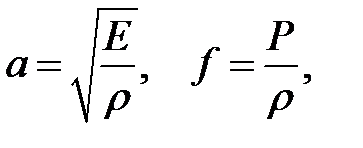
получим:
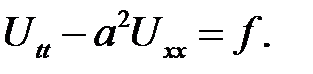
Теорема доказана.
Чтобы определить движение реального стержня, то есть найти единственное решение уравнения движения (22.1), нужно указать, в каких механических условиях находится стержень. К этим условиям относятся начальные и граничные условия. В качестве начальных условий обычно берут начальные смещения 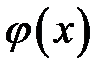 сечений стержня и начальные скорости
сечений стержня и начальные скорости 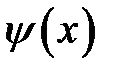 этих сечений
этих сечений
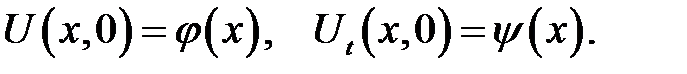
Если стержень ограничен и располагается на участке 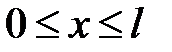 , то граничными условиями служат условия на концах стержня. Рассмот-рим примеры граничных условий.
, то граничными условиями служат условия на концах стержня. Рассмот-рим примеры граничных условий.
1. Концы стержня закреплены 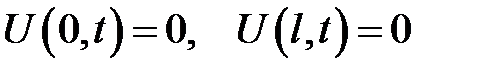 .
.
2. Левый конец закреплен, на правый действует сила F(t):
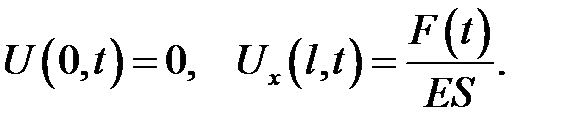 (22.8)
(22.8)
В самом деле, равенство (22.5) дает F(x, t) = ESUx. Подставив сюда координату правого конца х = l, получим условие (22.8) на этом конце, в котором F(t) = F(l, t).
3. Левый конец закреплен, правый свободен:
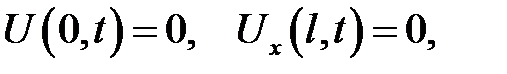 (22.9)
(22.9)
так как на правом конце F(l, t) = 0, поэтому из (22.8) вытекает (22.9).
Дата: 2018-09-13, просмотров: 1501.