Теорема
Собственные функции
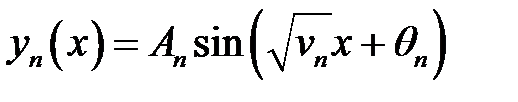 (28.1)
(28.1)
задачи (27.1) — (27.3) удовлетворяют условию:
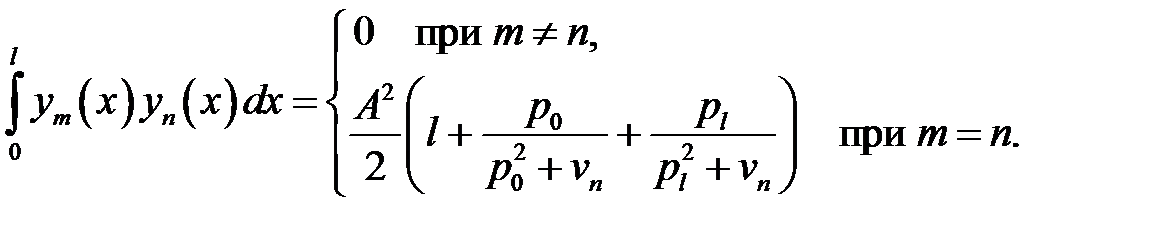 (28.2)
(28.2)
Доказательство.
Дано
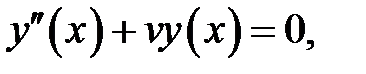 (1)
(1)
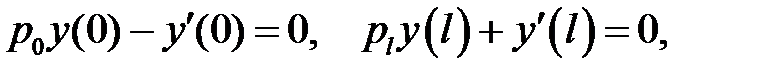 (2)
(2)
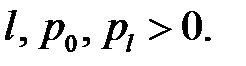 (3)
(3)
Тогда:
(2) → 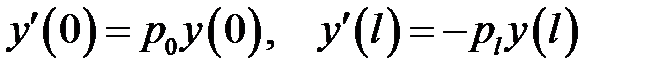 (4)
(4)
Задача (1) — (3) совпадает с задачей (27.1) — (27.3), поэтому:
(27.6) → 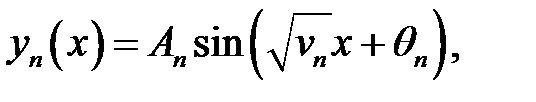 (5)
(5)
(1) → 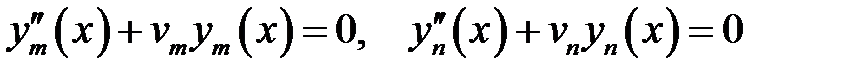
или 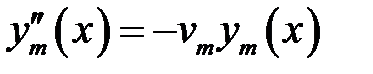 (6)
(6)
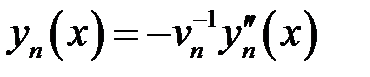 (7)
(7)
Вычислим интеграл в формуле (28.2).
Пусть 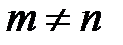 . (8)
. (8)
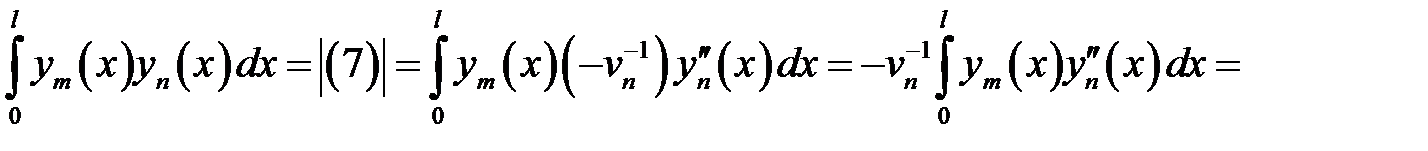
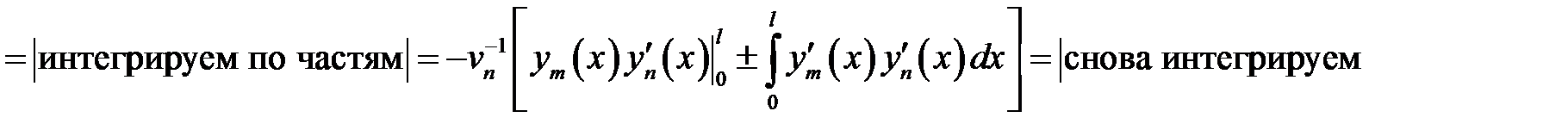
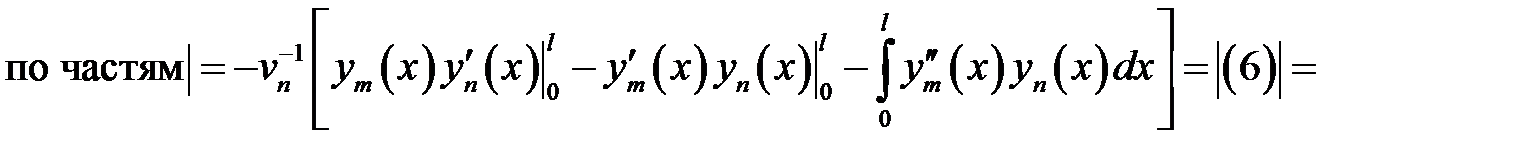
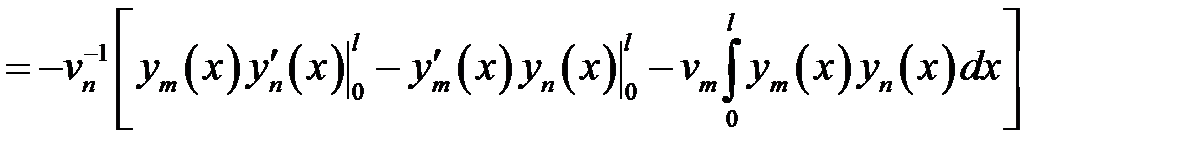 (9)
(9)
(9) →
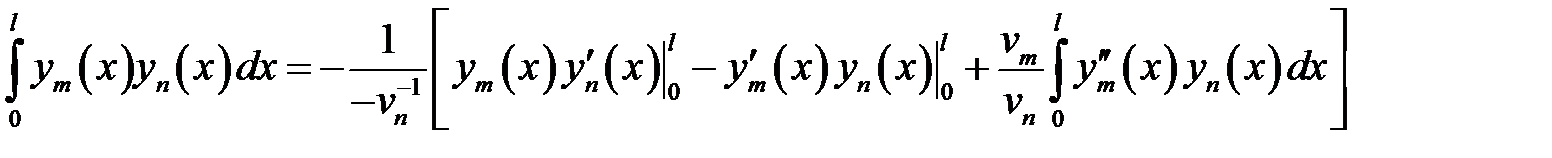
или 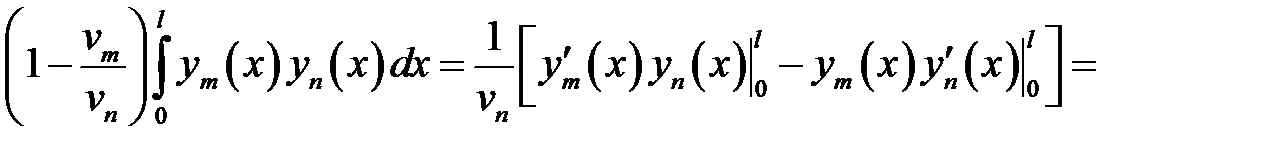
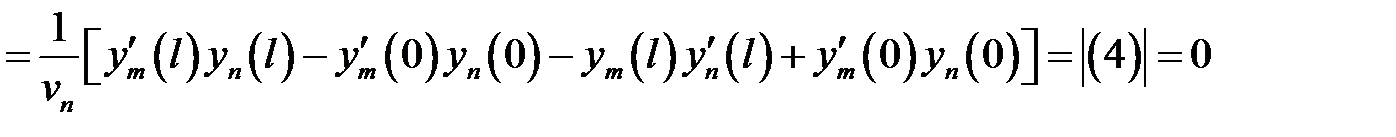 , т.е.
, т.е.
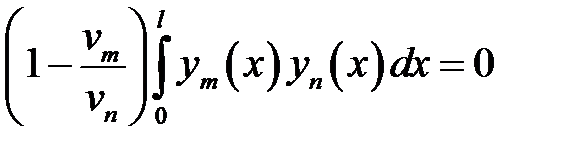 (10)
(10)
(8) → 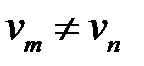 (11)
(11)
(10), (11) → 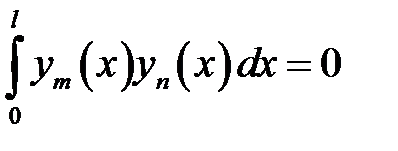 .
.
Пусть m = п
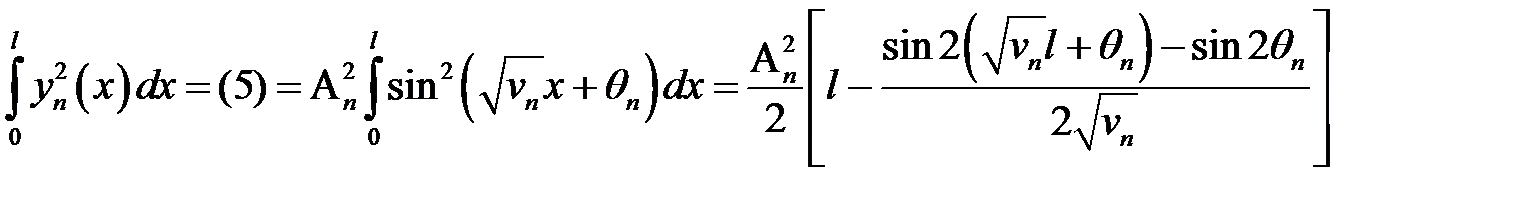 (12)
(12)
Решение однородного уравнения теплопроводности
Теорема 1
Уравнение
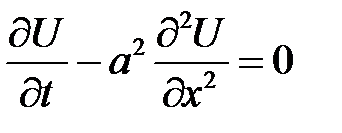
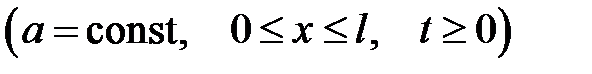
с начальным условием:
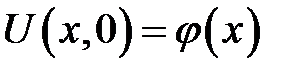
и однородными граничными условиями:
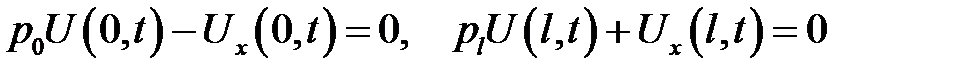
имеет следующее решение:
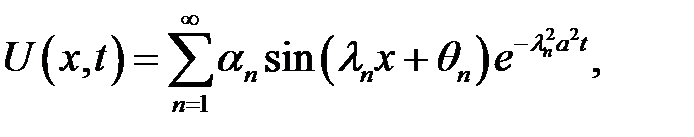
в котором 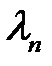 ,
, 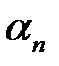 ,
, 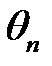 находятся из равенств:
находятся из равенств:
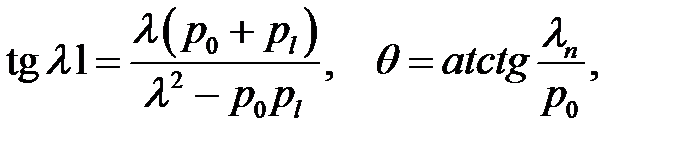
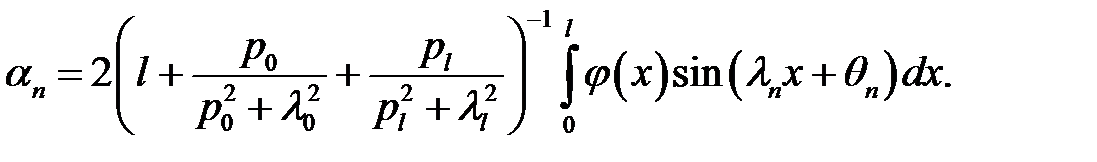
Доказательство.
Дано:
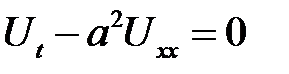 (1)
(1)
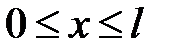 (2)
(2)
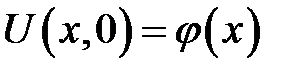 (3)
(3)
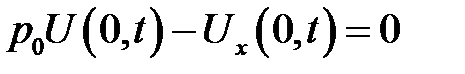 (4)
(4)
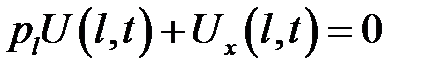 (5)
(5)
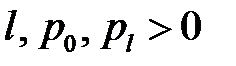 (6)
(6)
Частное решение однородного уравнения (1), удовлетворяющее однородным условиям (4), (5), будем искать в виде:
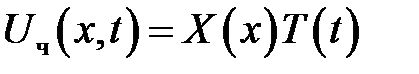 (7)
(7)
(1), (7) → 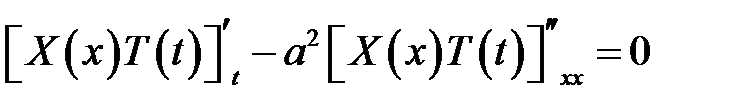
или
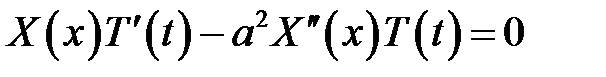
или 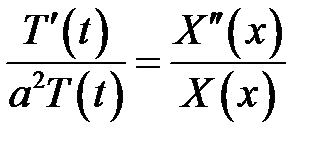 (8)
(8)
Здесь левая часть, не содержащая х, равна правой части, не со-держащей t. Значит, левая часть не может содержать t, правая часть не может содержать х. Таким образом, как левая, так и правая части не содержат ни х, ни t, т. е. обе части являются константами.
(8) → 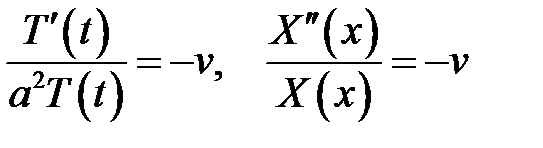 , где v = const (9)
, где v = const (9)
(9) → 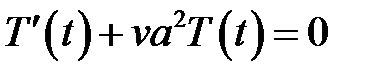 (10)
(10)
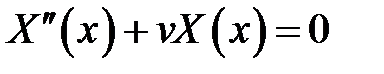 (11)
(11)
(4), (7) → 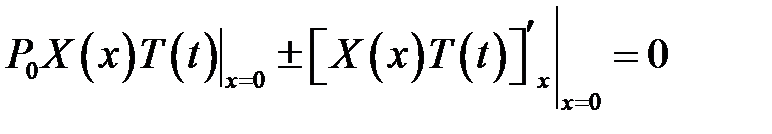
или
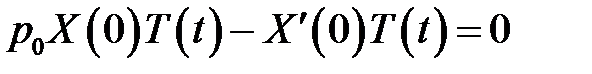
или 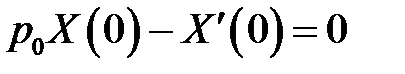 (12)
(12)
(5), (7) → 
или
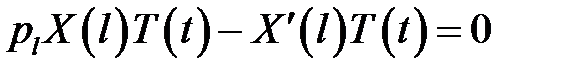
или 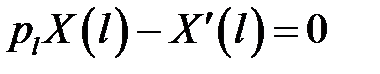 (13)
(13)
Задача (11) — (13), (2), (6) совпадает с задачей (27.1) — (27.3), поэтому в (11) v> 0 и если положить 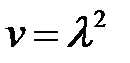 , (14)
, (14)
получим:
(27.5), (14) → 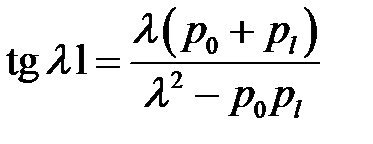 (15)
(15)
Решив это уравнение, найдем корни 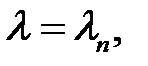 (n = 1, 2, ..,
(n = 1, 2, .., 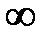 ):
):
(27.7), (14), (15) → 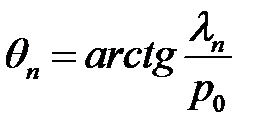 (16)
(16)
(27.6), (14), (15), (16) → 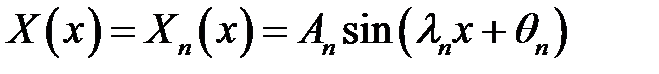 (17)
(17)
(10), (14), (15) → 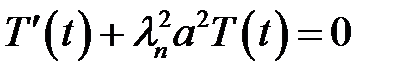 , отсюда
, отсюда
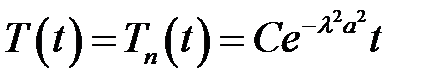 (18)
(18)
(7), (17), (18) → 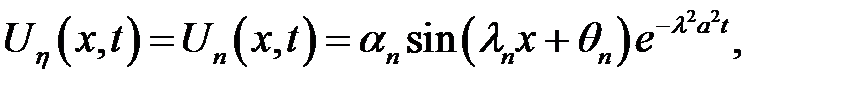 (19)
(19)
где обозначено 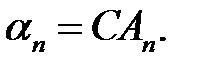
Итак, мы нашли функции 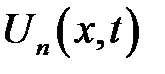 , которые удовлетворяют равен-ствам (1), (3), (4). Тогда этим же равенствам будет удовлетворять функция:
, которые удовлетворяют равен-ствам (1), (3), (4). Тогда этим же равенствам будет удовлетворять функция:
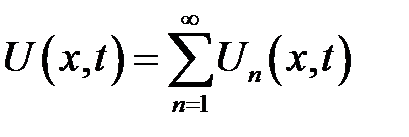 (20)
(20)
(20), (19) → 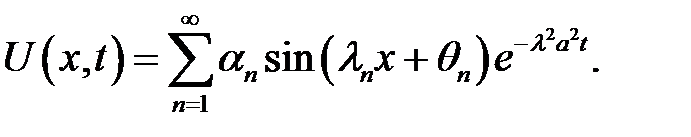 (21)
(21)
Здесь 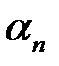 — произвольные постоянные. Поэтому мы можем взять такие
— произвольные постоянные. Поэтому мы можем взять такие 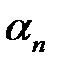 , чтобы выполнялось условие (3). Будем иметь:
, чтобы выполнялось условие (3). Будем иметь:
(21), (3) → 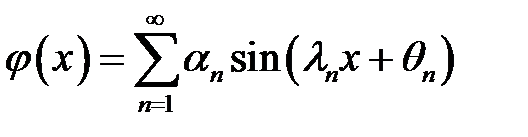 (22)
(22)
Введем обозначение 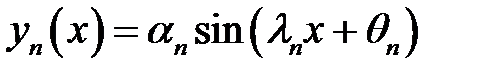 (23)
(23)
(22), (23) → 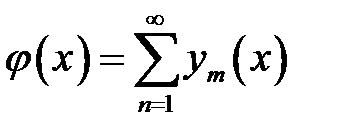 (24)
(24)
Умножим обе части равенства на у n(х).
(24) → 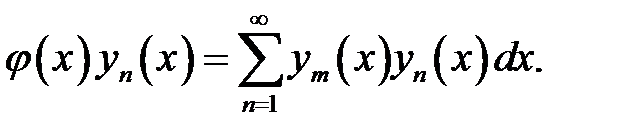 (25)
(25)
Проинтегрируем обе части по интервалу 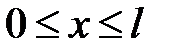 :
:
(25) → 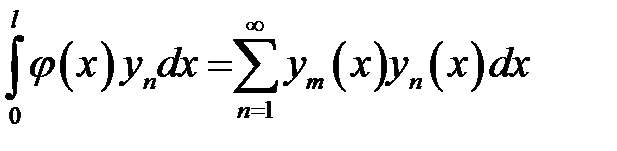 (26)
(26)
Функции (23) имеют вид (28.1), поэтому они ортогональны.
(26), (28.2) →
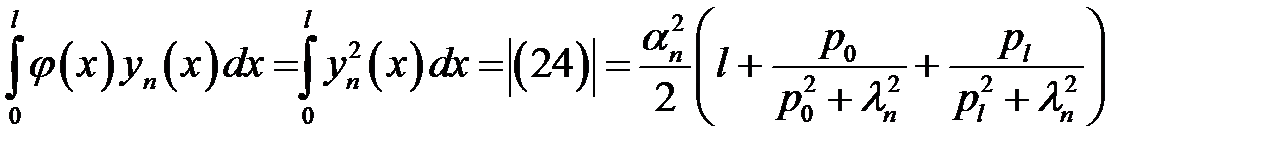 (27)
(27)
(27), (23) → 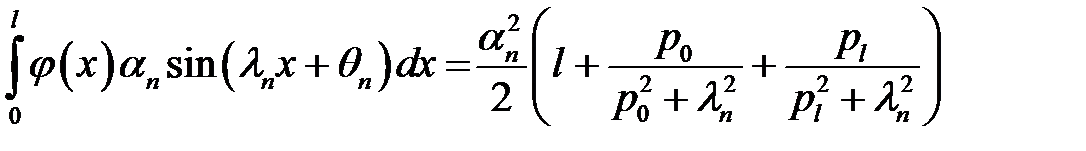
или
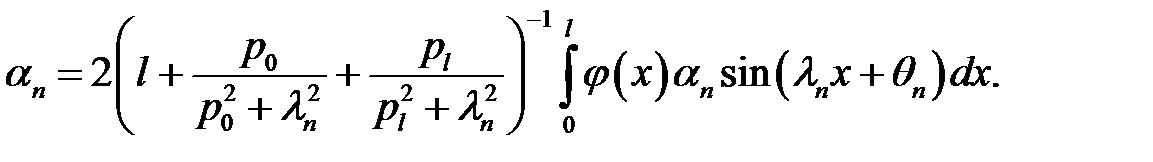
Теорема доказана.
Теорема 2
Уравнение
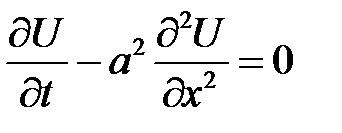
с начальным условием:
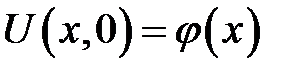
и неоднородными граничными условиями:
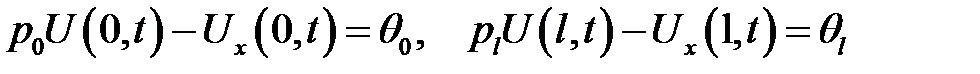
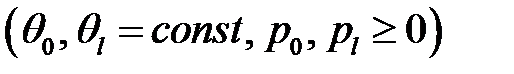
имеет следующее решение:
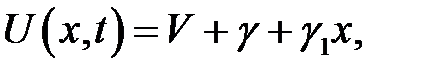
где 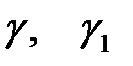 находятся из системы:
находятся из системы:
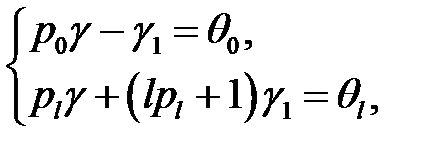
а функция V(x, t) есть решение уравнения с начальным условием:
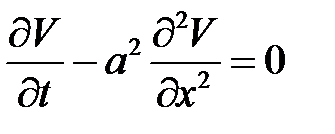 ,
,
с начальным условием:
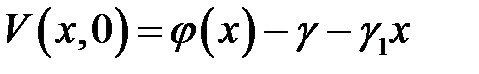
и однородными граничными условиями:
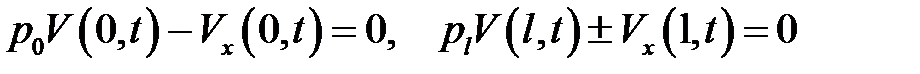 .
.
Доказательство.
Дано:
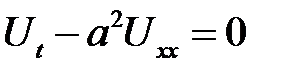 (1)
(1)
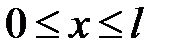 (2)
(2)
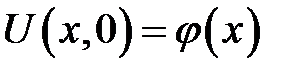 (3)
(3)
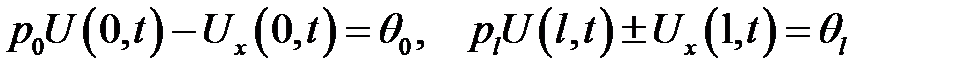 (4)
(4)
где 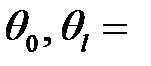 const
const
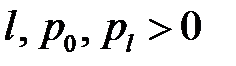 (5)
(5)
Решение уравнения (1) будем искать в виде:
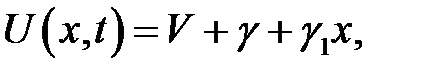 (6)
(6)
где 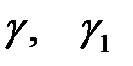 = const (7)
= const (7)
(6),(7) → 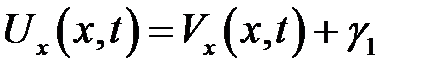 (8)
(8)
(4), (6), (8) → 
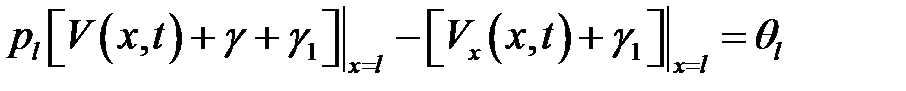
или
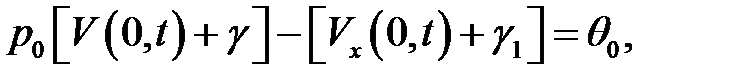
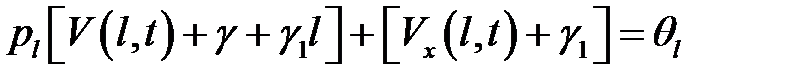
или
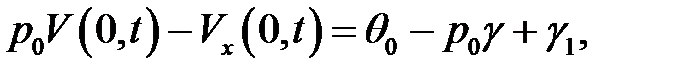
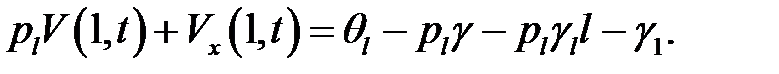 (9)
(9)
Возьмем такие значения  , чтобы правые части равнялись нулю (10)
, чтобы правые части равнялись нулю (10)
(9), (10) → 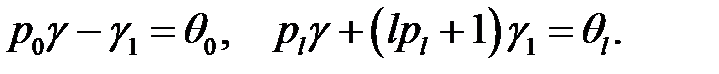 (11)
(11)
(11) → находим 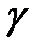 и
и 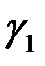
(9), (10) → 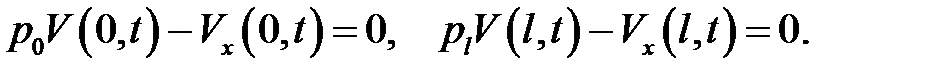 (12)
(12)
(12) → V(x, t) удовлетворяет однородным граничным условиям
(1), (6) → 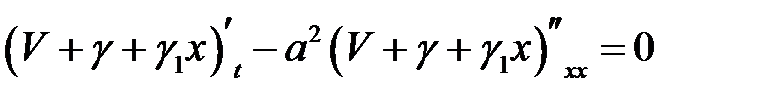
или
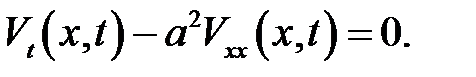
(6) → 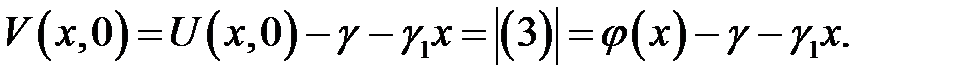
Теорема доказана.
Основные понятия метода сеток
Решение уравнений математической физики в аналитической форме (то есть в виде ряда или интеграла) возможно в редких слу-чаях. Одним из методов приближенного решения является метод се-ток (он же метод конечных разностей). Пусть переменная х изменя-ется в интервале [а, b]. Нанесем п– 1 точек а<х1<х2< ... <x n -1<b и положим х0 = а, х n = b. Множество точек {х0, х1, х2, …, х n} называется одномерной сеткой, а сами точки называются узлами сетки. Рассто-яние между соседними узлами 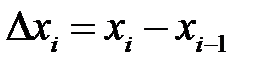 называется шагом сетки. Если не все
называется шагом сетки. Если не все 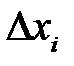 , одинаковы, то сетку называют неравномерной. Если все
, одинаковы, то сетку называют неравномерной. Если все 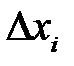 , одинаковы,
, одинаковы, 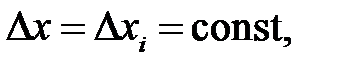 то сетку называют равномерной. В этом случае
то сетку называют равномерной. В этом случае 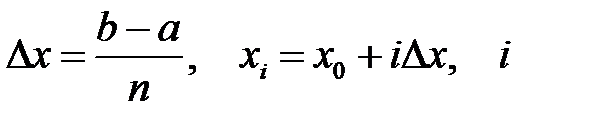 = 1, ..., п. Функцию
= 1, ..., п. Функцию 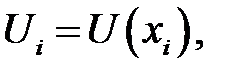 определенную в узлах сетки, называют сеточной функцией.
определенную в узлах сетки, называют сеточной функцией.
Пусть область изменения двух переменных (х, t) есть прямо-угольник 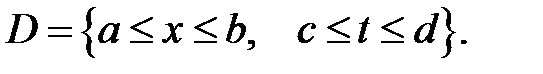 Через точки
Через точки 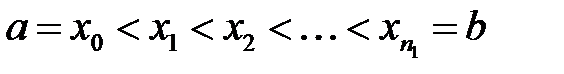 проведем прямые х = х i, а через точки
проведем прямые х = х i, а через точки  проведем прямые t = t j. Получим множество точек пересечения (х i, t j), называемое двумерной прямоугольной сеткой. Пусть U— сеточная функция, определенная на двумерной сетке. Будем обозначать через
проведем прямые t = t j. Получим множество точек пересечения (х i, t j), называемое двумерной прямоугольной сеткой. Пусть U— сеточная функция, определенная на двумерной сетке. Будем обозначать через 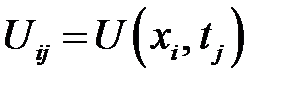 значение сеточной функции в узле (х i, t j).
значение сеточной функции в узле (х i, t j).
Аппроксимация производных
Разложим функцию U(x) в ряд Тейлора в окрестности точки х:
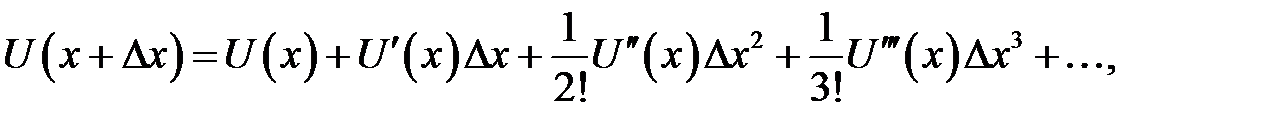 (31.l)
(31.l)
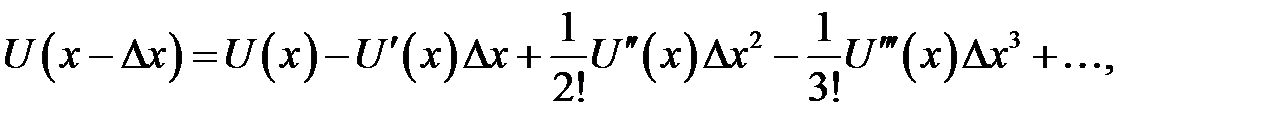 (31.2)
(31.2)
С помощью этих разложений найдем формулы приближенного вычисления производных. Из (31.1) находим:
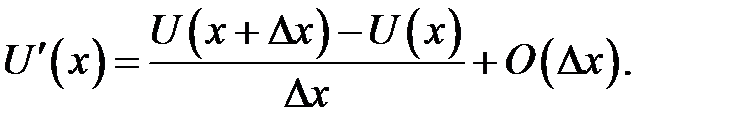 (31.3)
(31.3)
Дробь, стоящая в правой части, называется правым разностным отношением. Из ряда (31.2) находим:
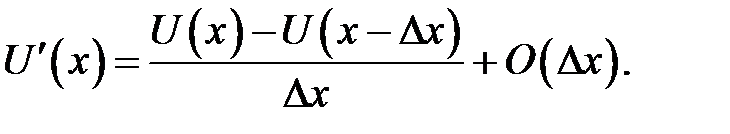 (31.4)
(31.4)
Дробь в правой части называется левым разностным отноше-нием. Если из ряда (31.1) вычесть ряд (31.2), получится новый ряд, из которого найдем:
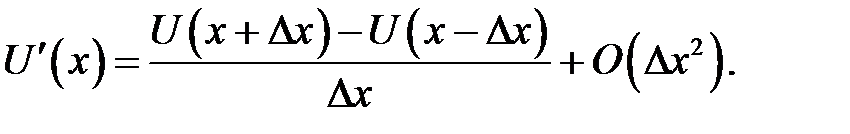 (31.5)
(31.5)
Дробь в правой части называется центральным разностным от-ношением. Из трех последних формул формула (31.5) дает большую точность. Более точные формулы приближенного вычисления правой и левой производной можно получить следующим образом. Возьмем разложение:
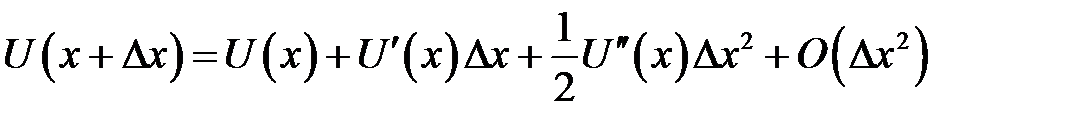 (31.6)
(31.6)
и заменим  на 2
на 2  . Получим:
. Получим:
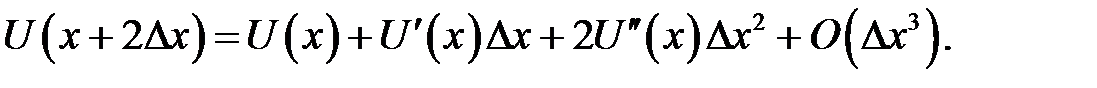 (31.7)
(31.7)
Равенство (31.6) умножим на –4 и прибавим к (31.7). Мы найдем:
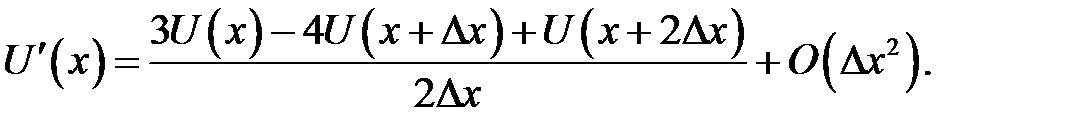 (31.8)
(31.8)
Если заменить 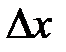 на –
на – 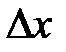 , то:
, то:
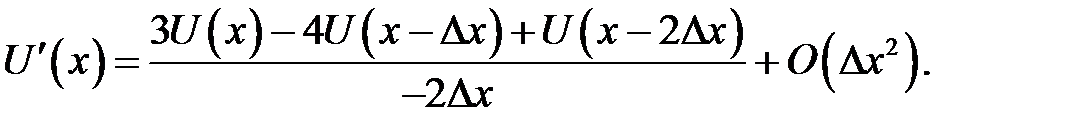 (31.9)
(31.9)
По формулам (31.8), (31.9) вычисляются соответственно левая и правая производные в точке х.
Сложим ряды (31.1) и (31.2). Из полученного ряда найдем:
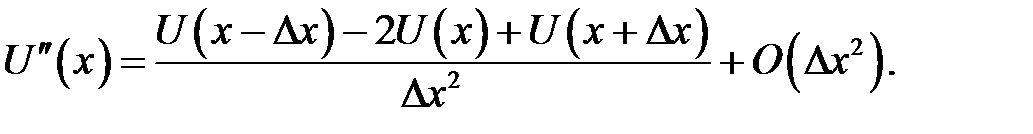 (31.10)
(31.10)
Теперь посмотрим, как вычисляются эти производные в узлах равномерной одномерной сетки, когда дана сеточная функция 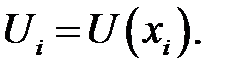 В силу равенств
В силу равенств 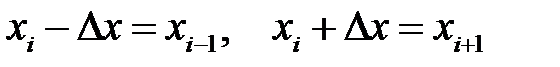 по формулам (31.3) — (31.5) и (31.10) получаем соответственно:
по формулам (31.3) — (31.5) и (31.10) получаем соответственно:
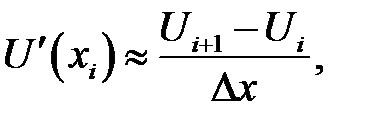
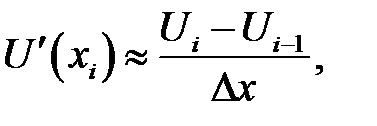
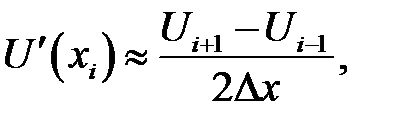
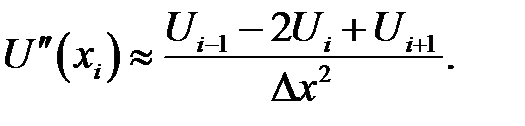 (31.11)
(31.11)
Правые части этих формул аппроксимируют (приближенно заменяют) производные разностными отношениями. В аппроксимациях первой производной участвуют значения сеточной функции в двух узлах. Поэтому говорят, что для вычисления первой производной применяется двухточечный шаблон или шаблон, состоящий из двух узлов. Вообще, множество узлов, координаты которых участвуют при вычислении производной, называется шаблоном данной производной. Последняя аппроксимация в (31.11) показывает, что для вычисления второй производной применяется трехточечный шаблон.
Дата: 2018-09-13, просмотров: 1059.