Пусть один конец вала х = 0 закреплен, а на другой конец х = I насажен массивный диск, момент инерции которого равен J1. В начальный момент диск закручен на малый угол 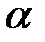 и отпускается без начальной скорости. Найдем
и отпускается без начальной скорости. Найдем 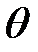 (х, t) — угол поворота сечений вала.
(х, t) — угол поворота сечений вала.
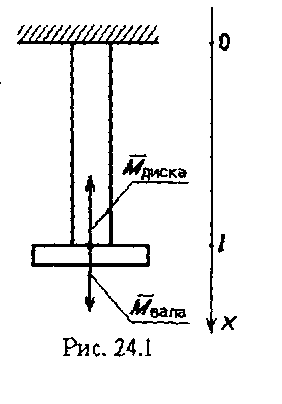
Рис. 24.1
Решение.
Прежде всего составим два начальных и два граничных условия и решим затем уравнение (23.1).
Конец вала х = 0 неподвижен, поэтому 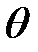 (0, t) = 0. (1)
(0, t) = 0. (1)
Это первое граничное условие.
Начальная угловая скорость всех сечений равна нулю
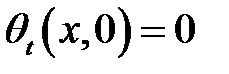 (2)
(2)
При t = 0 конец вала х = l закручен на угол 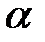 , так что
, так что
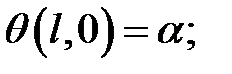 (3)
(3)
Равенства (2) и (3) задают начальные условия. Вследствие того, что нижний конец вала закручен, в сечениях действует сила сдвига. Найдем ее.
Возьмем сечение S(x) и на нем бесконечно малый участок dS, располагающийся на расстоянии r от оси вала. Тогда
(23.2) → 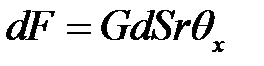 (4)
(4)
есть сила сдвига, действующая на участок dS, поэтому сила, действу-ющая на все сечение S(x) равна:
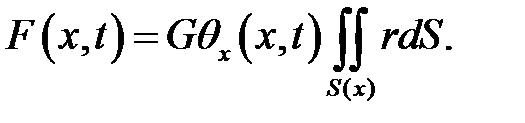 (5)
(5)
Введем обозначение 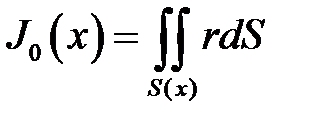 (6)
(6)
полярный статический момент сечения S(x).
(5), (6) → 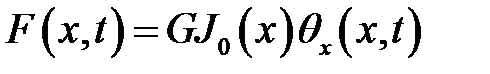 или
или
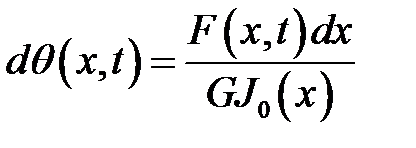 (7)
(7)
Будем считать, что поперечные сечения вала одинаковы,S(х) = S, тогда:
(6) → 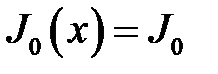 . (8)
. (8)
Будем также считать, что при t= 0 во всех сечениях действует одна и та же сила:
F(x,0) = F. (9)
(7),(8),(9) → 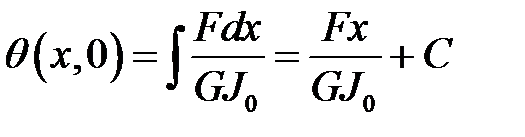 (10)
(10)
(10), (1) → 0 = С (11)
(10),(11) → 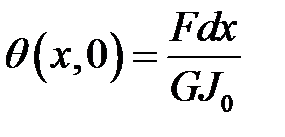 (12)
(12)
(12),(3) → 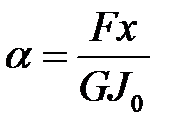 или
или 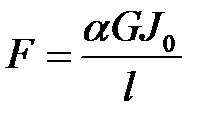 (13)
(13)
(12), (13) → 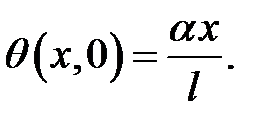
Это второе граничное условие.
В сечении х = l, где соединяются вал и диск (рис. 24.1), имеем:
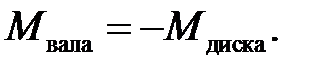 (14)
(14)
Но 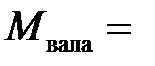 (23.3) =
(23.3) = 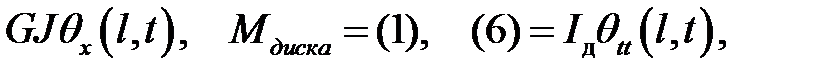 (15)
(15)
где Iд— момент инерции диска, 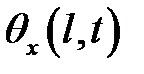 — угловое ускорение диска.
— угловое ускорение диска.
(14), (15) → 
или
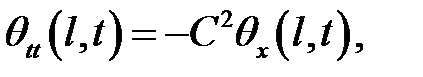 (16)
(16)
где обозначено 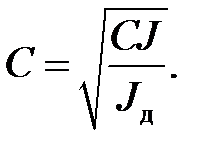 Выражение (16) дает второе граничное условие. Теперь будем искать решение уравнения свободных кру-тильных колебаний.
Выражение (16) дает второе граничное условие. Теперь будем искать решение уравнения свободных кру-тильных колебаний.
Теорема
Уравнение
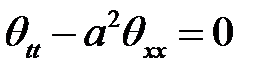
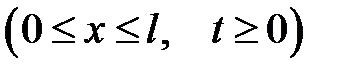
с начальными условиями:
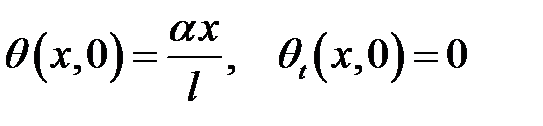
и граничными условиями
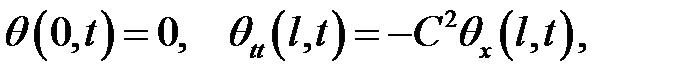
имеет следующее решение:
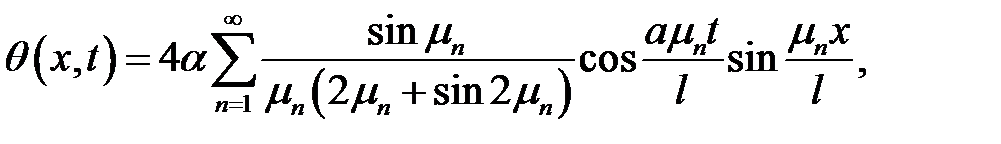
в котором 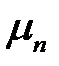 — положительные корни уравнения:
— положительные корни уравнения:
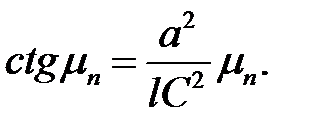
Доказательство.
Дано 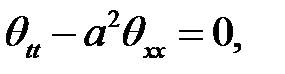 (1)
(1)
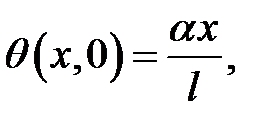 (2)
(2)
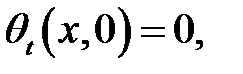 (3)
(3)
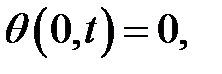 (4)
(4)
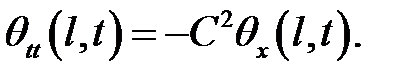 (5)
(5)
Искомую функцию представим в виде:
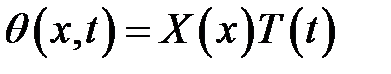 (6)
(6)
(1), (6) → 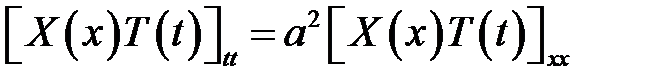
или
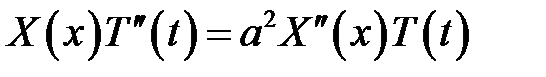
или
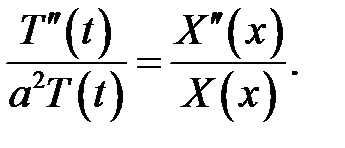 (7)
(7)
Здесь левая часть не содержит переменной х, правая часть не содержит t. Поэтому они совпадают только тогда, когда они не зависят ни от х ни от t, т. е. когда они постоянны.
Обозначим их общую постоянную через 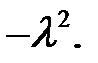 (8)
(8)
(Докажите самостоятельно, что из условий, налагаемых на Х(х), следует отрицательность общей постоянной).
(7), (8) → 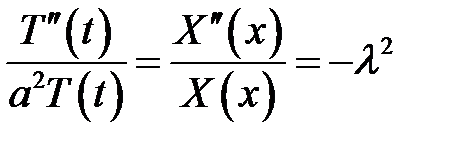
или
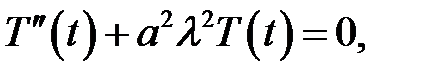 (9)
(9)
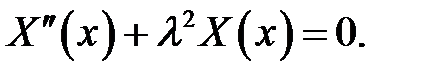 (10)
(10)
Для решения уравнения (10) воспользуемся граничными условиями (4) и (5).
(4),(6) → 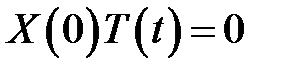 (11)
(11)
В виду того, что T(t) — переменная величина, т. е. не всегда T(t) = 0, то:
(11) → 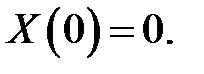 (12)
(12)
(5), (6) → 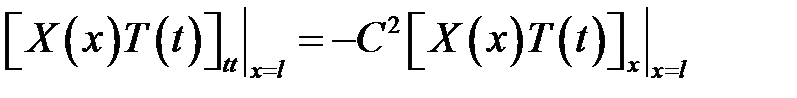
или
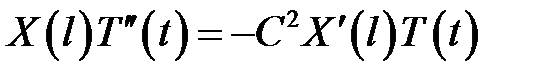 (13)
(13)
(9), (13) → 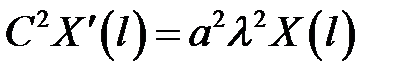 (14)
(14)
Равенства (12), (14) задают граничные условия для уравнения (10).
(10) → общее решение 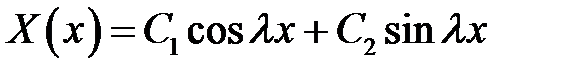 (15)
(15)
(12), (15) → С1=0 (16)
(15), (16) → 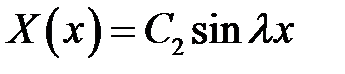 (17)
(17)
(14), (17) → 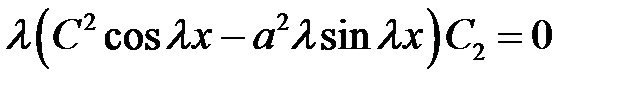 (18)
(18)
Так как 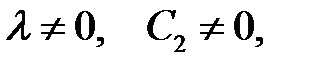 (иначе (17) →
(иначе (17) → 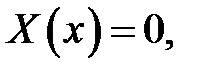
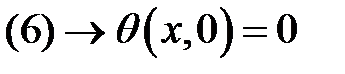 — противоречит условию (2), то (18) →
— противоречит условию (2), то (18) → 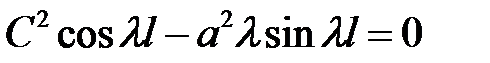 или
или
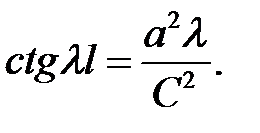 (19)
(19)
Уравнение (19) позволяет найти 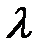 .
.
Покажем, что решением (19) является бесконечная последова-тельность чисел 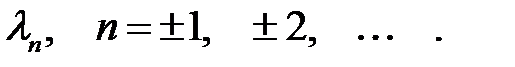
Положим 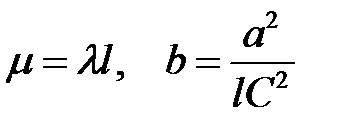 (20)
(20)
(19),(20) → 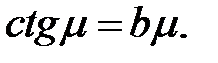 (21)
(21)
Выражение (21) показывает, что если положительное число 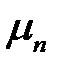 является решением уравнения (21), то и число
является решением уравнения (21), то и число 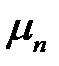 также будет решением. Поэтому нам достаточно найти положительные корни этого уравнения. Построим графики функций
также будет решением. Поэтому нам достаточно найти положительные корни этого уравнения. Построим графики функций 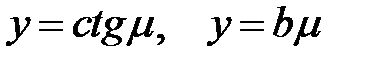 (рис. 24.2).
(рис. 24.2).
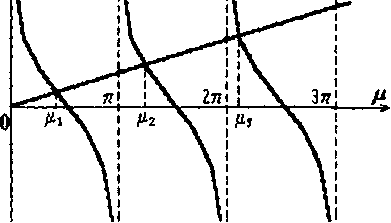
Рис. 24.2
Опустив перпендикуляры на ось О 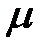 , получаем корни уравнения (14)
, получаем корни уравнения (14) 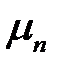 , где n— номер корня, n = 1, 2,.... Соответствующим отрицательным корням
, где n— номер корня, n = 1, 2,.... Соответствующим отрицательным корням 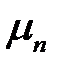 припишем отрицательные номера, положим
припишем отрицательные номера, положим 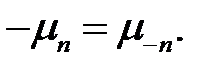 (22)
(22)
Современными компьютерными методами можно найти любой корень уравнения (14) с любой точностью.
Далее будем предполагать, что 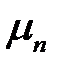 нам известны.
нам известны.
Теперь вместо 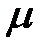 будем подставлять корни
будем подставлять корни 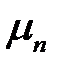 . Соответствующие значения, зависящие от
. Соответствующие значения, зависящие от 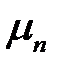 , будем обозначать индексом n.
, будем обозначать индексом n.
(20) → 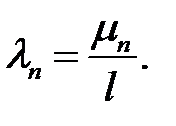 (23)
(23)
(23), (17) → 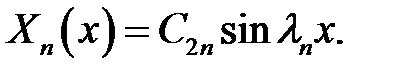 (24)
(24)
Это есть решение уравнения (10) при 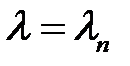 .
.
(9), (23) → 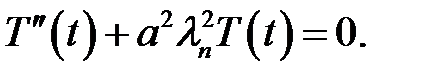 (25)
(25)
(25) → находим общее решение, соответствующее корню 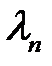
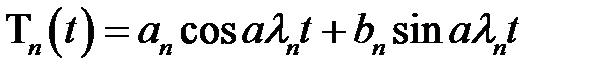 (26)
(26)
(6), (24), (26) → 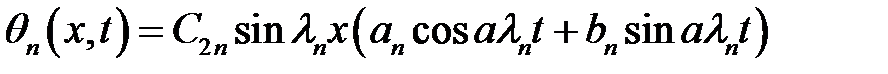 (27)
(27)
Обозначим 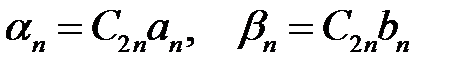 (28)
(28)
(27), (28) → 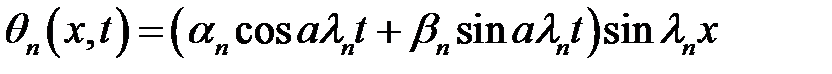 (29)
(29)
Чтобы удовлетворить начальным условиям (2), (3) решение ищем в виде суммы:
(29) → 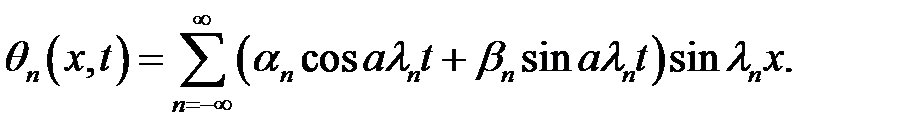 (30)
(30)
Сгруппируем в пары члены с номерами n и –n
(30)→ 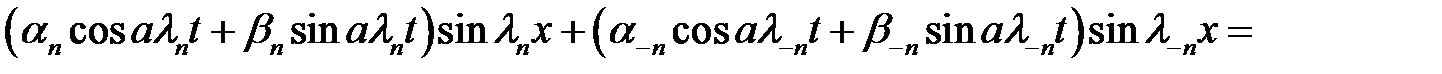
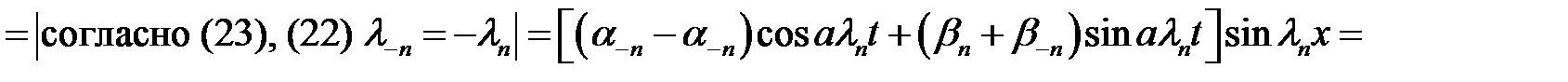
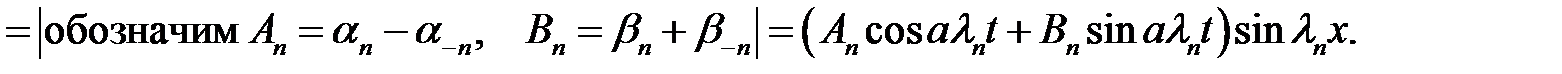 (31)
(31)
(30), (31) → 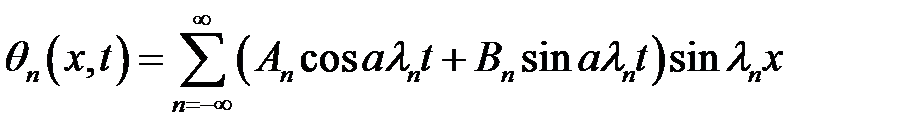 (32)
(32)
Для определения An, B n воспользуемся начальными условиями.
(2), (32) → 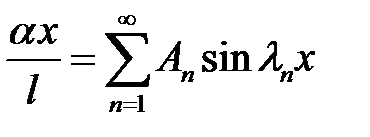 (33)
(33)
(3), (32) → 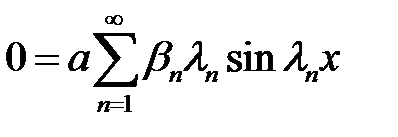 (34)
(34)
На [0, l] функции 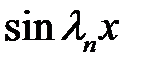 не ортогональны, т. е. если
не ортогональны, т. е. если
 .
.
Продифференцируем (33) и (34) по х:
(33) → 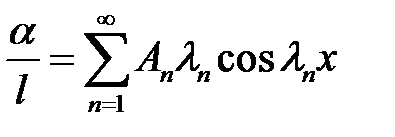 (35)
(35)
(34) → 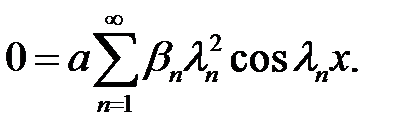 (36)
(36)
Покажем, что функции 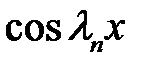 ортогональны на [0, l]. Пусть
ортогональны на [0, l]. Пусть 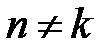 .
.
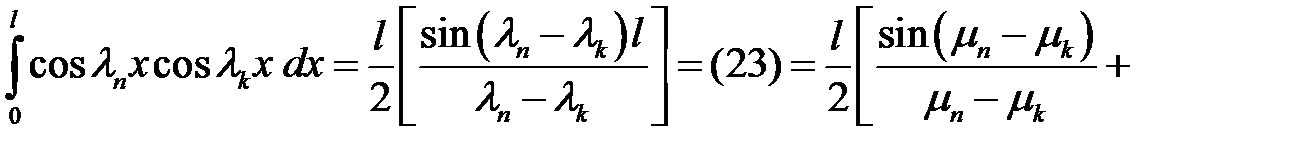
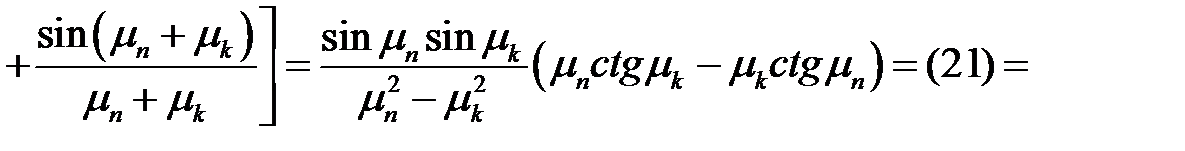
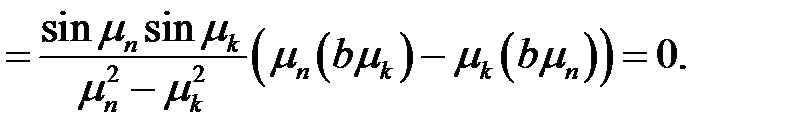 (37)
(37)
Таким образом, ортогональность доказана.
Пусть п = k.
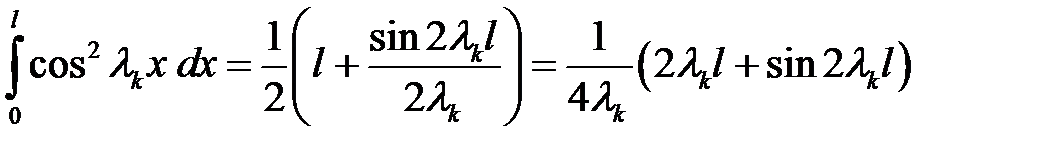 (38)
(38)
(38) → 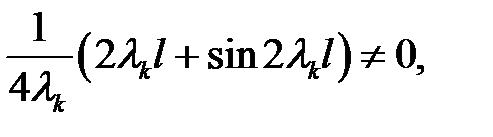 (39)
(39)
т. к. это значение получено интегрированием функции 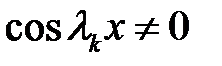 . Итак
. Итак
(37), (38) → 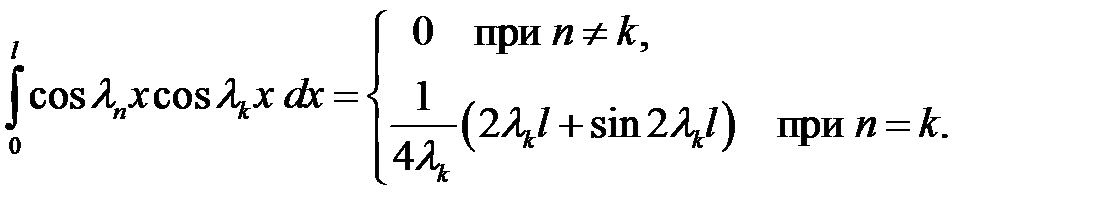 (40)
(40)
Обе части равенства (36) умножим на 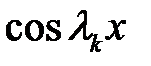 и проинтегрируем в интервале [0, l].
и проинтегрируем в интервале [0, l].
(36) → 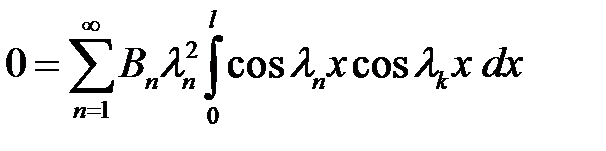 (41)
(41)
(40), (41) → 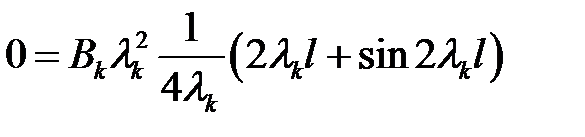 (42)
(42)
(39), (42) → 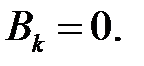 (43)
(43)
Обе части равенства (35) умножим на 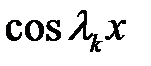 и проинтегрируем в интервале [0, l].
и проинтегрируем в интервале [0, l].
(35) → 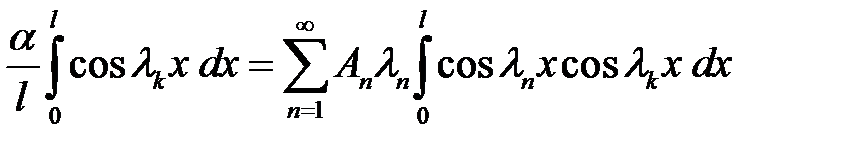 (44)
(44)
(44), (40), (23) → 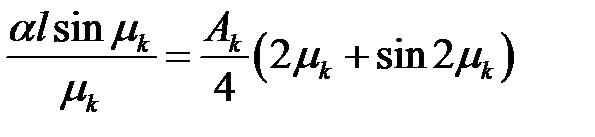 или
или
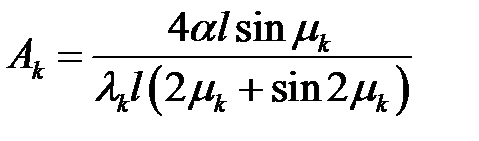 (45)
(45)
(32), (43), (45) → 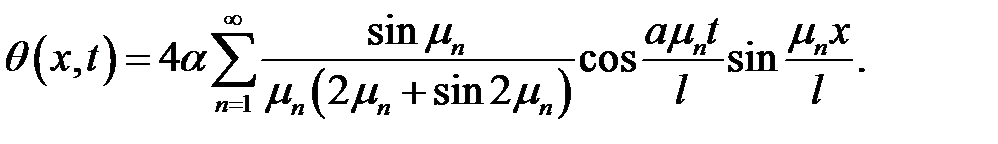
Теорема доказана.
Дата: 2018-09-13, просмотров: 930.