Формулы (31.11) показывают, как при помощи сеточной функции производные аппроксимируются разностными отношениями. Рассмотрим несколько примеров применения этих формул для решения дифференциальных уравнений.
Пример 1.
Решить обыкновенное дифференциальное уравнение второго порядка:
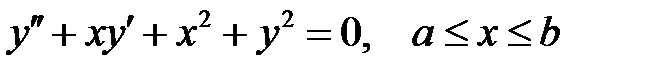(31.1)
с граничными условиями:
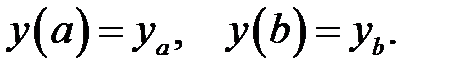
Разобьем участок [а, b] на п равных частей. Получится равно-мерная сетка с шагом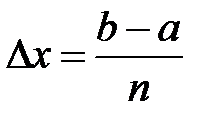 
. Так как х0 = а, то координаты точек деления (узлов сетки) будут равны 
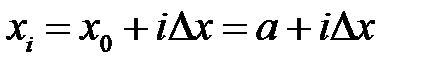, где i = 1, ..., n. Из граничных условий получаем 
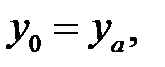у n= у b. В дифференциальном уравнении (32.1) заменим производные разностнымиотношениями. Получим:
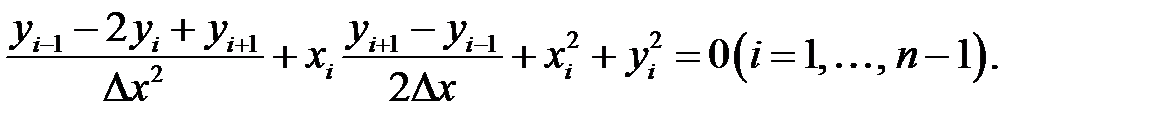
Эта система так называемых сеточных уравнений содержит п– 1 неизвестных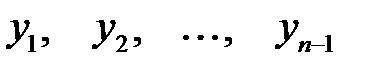 
. Так как число уравнений равно числу неизвестных, то система имеет решение.
Пример 2.
Решить волновое уравнение
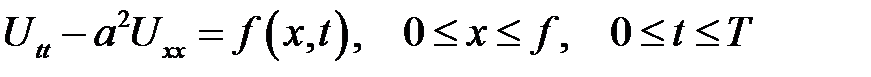(32.2)
с начальными условиями:
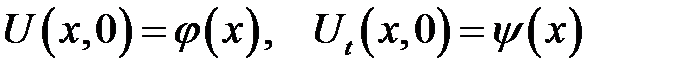
и граничными условиями:
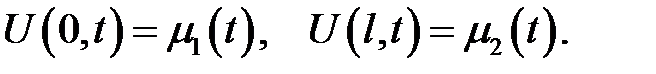
Область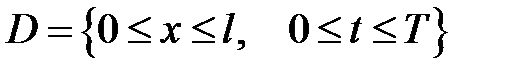 
покрываем равномерной сеткой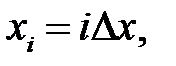 
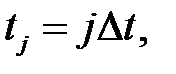где 
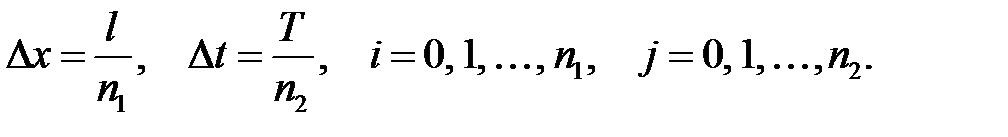Приме-ним формулу (31.10) для вычисления частных производных второго порядка:
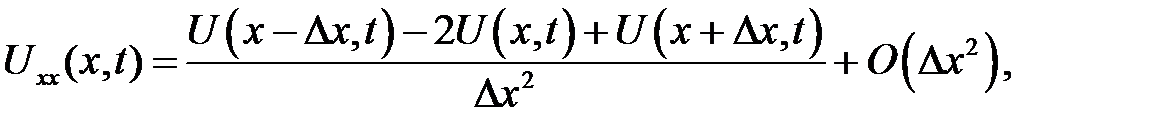
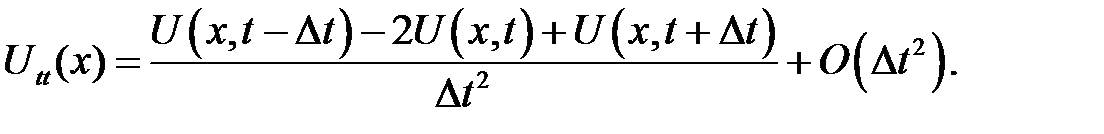
Введя сеточную функцию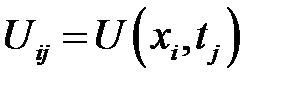 
, будем иметь:
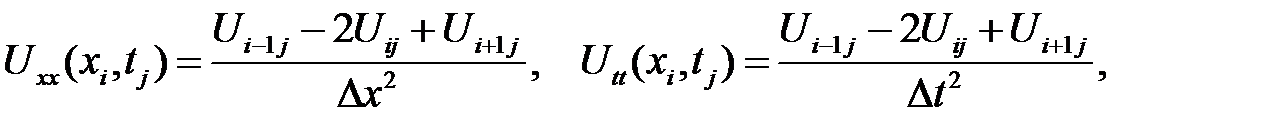
поэтому волновое уравнение (32.2) заменится на следующую систему сеточных уравнений:
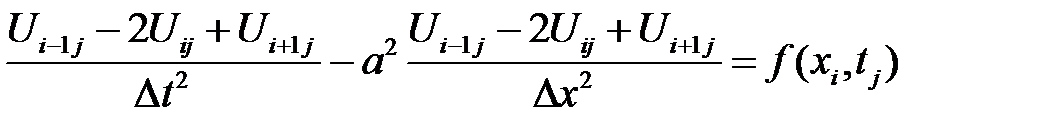
(i = 1, …, n1-1, j = 1, …, n2-1)
где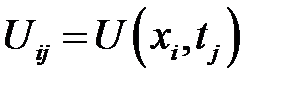 
. Присоединив сюда начальные и граничные условия:
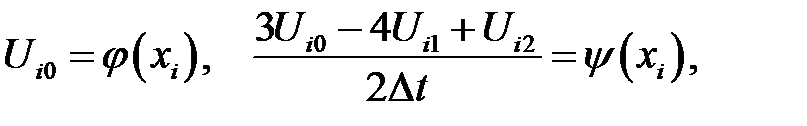i = 1, …, n1-1,
получим систему уравнений, позволяющую найти значения U(x, t) в узлах сетки.
Пример 3.
Решить уравнение теплопроводности
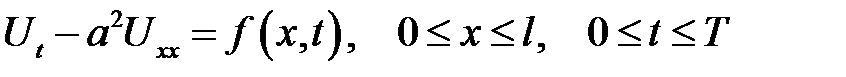(32.3)
с начальным условием:
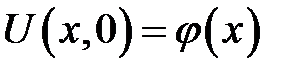
и граничными условиями:
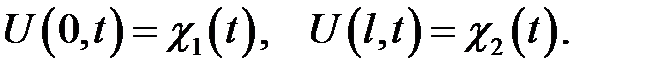
Область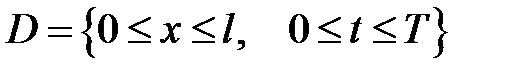 
покроем такой же сеткой, как в примере 2. Уравнение (32.3) заменится на систему:
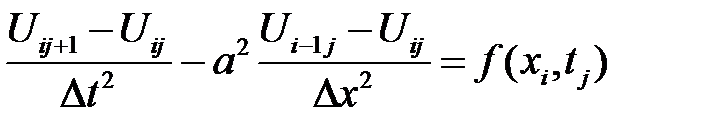(i = 1, …, n1-1, j = 1, …, n2-1)
с дополнительными условиями:
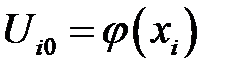(i = 1, …, n1-1),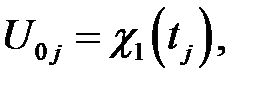 
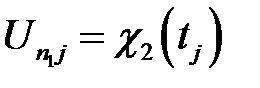(ij = 1, …, n2-1)
Теперь, на основе полученного опыта, мы можем сформули-ровать суть метода сеток: область изменения независимых перемен-ных покрывается сеткой (системой точек, называемых узлами), со-ставляется и решается система сеточных уравнений, соответ-ствующая данному дифференциальному уравнению. В результате мы найдем значения искомой функции во всех узлах сетки.
Задачи
33.1. Однородная струна, закрепленная на концах х = 0, х = l , имеет в начальный момент времени форму параболы, симметричной относительно перпендикуляра, проведенного через точку х = 
. Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
Решение.
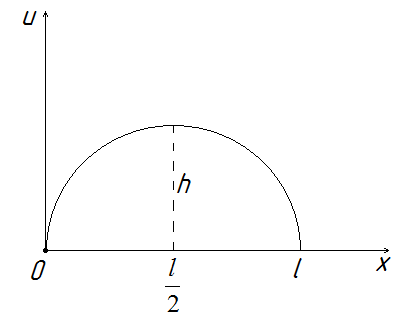
Рис.33.1
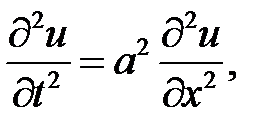
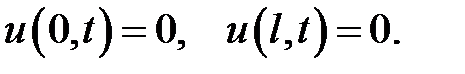
Начальные условия: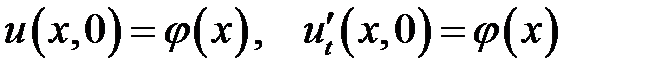 
.
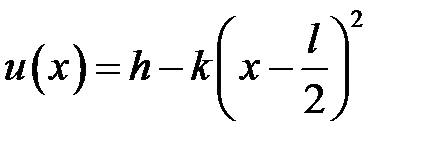, при х = 0 должно быть 
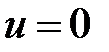. Тогда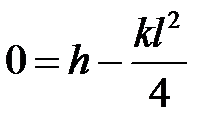 
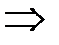
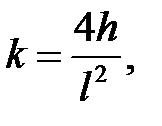
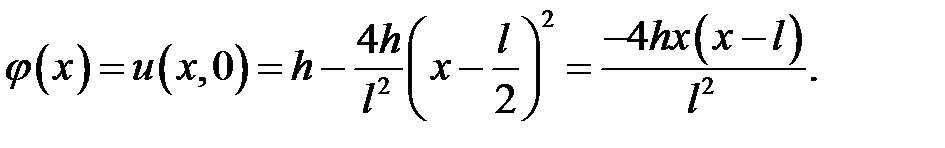
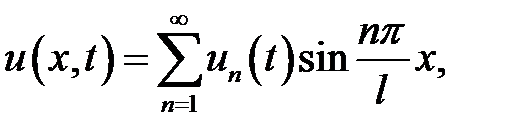
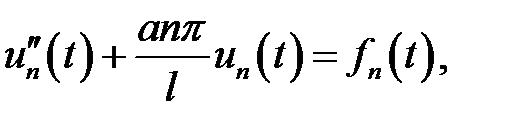
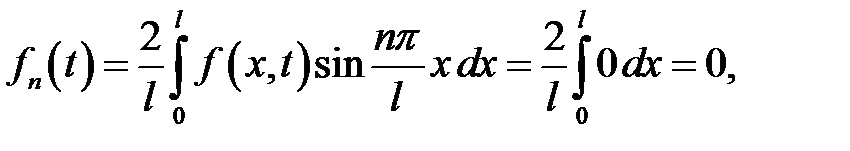
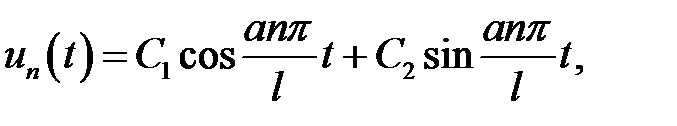
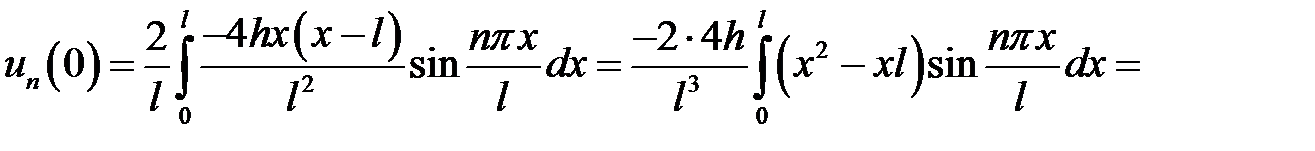
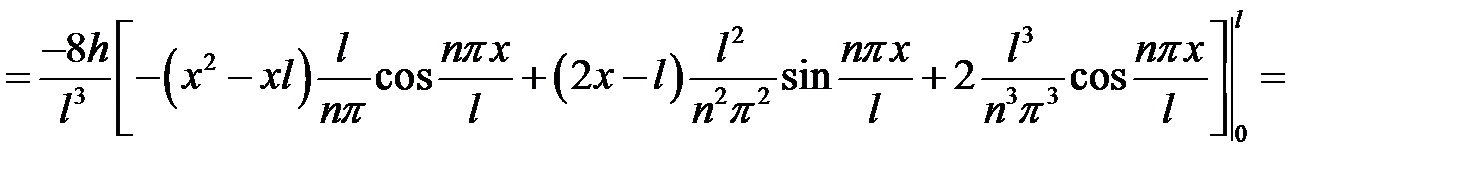
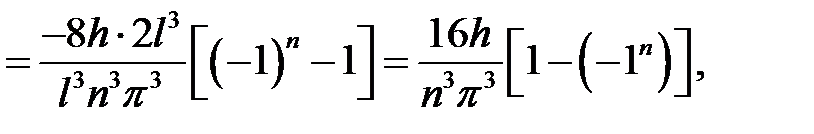
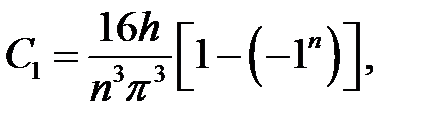
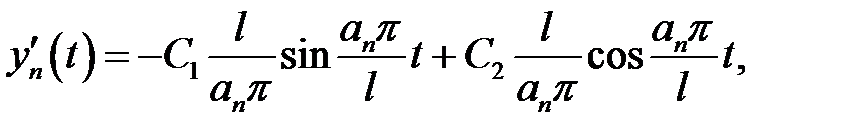
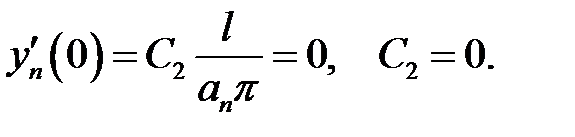
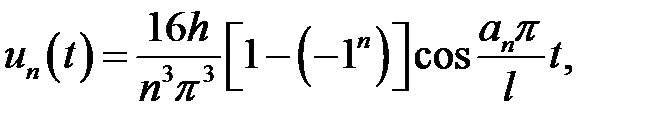
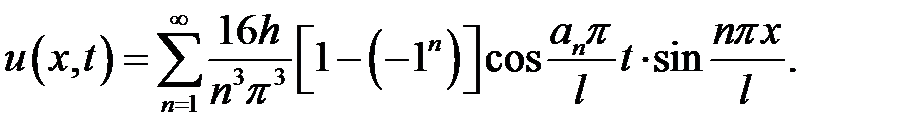
Если n – четное,  ,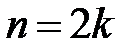
то  ,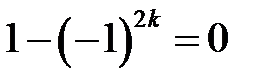
| Если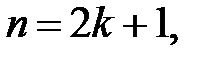 
то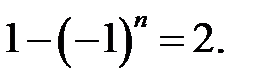 
|
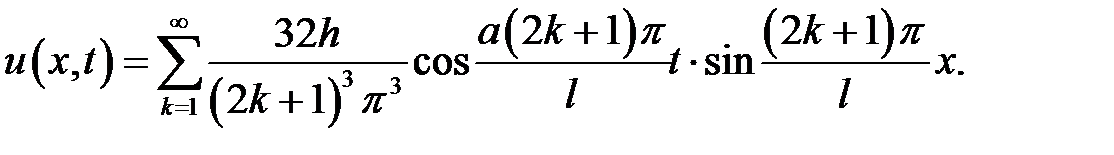
33.2. Однородная струна, закрепленная на концах х = 0, х = l, имеющая в начальный момент времени форму параболы, симмет-ричной относительно перпендикуляра, проведенного через точку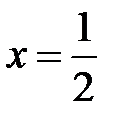 
. Определить смещение точек струны от прямолинейного поло-жения равновесия, предполагая, что начальные скорости отсутст-вуют.
Ответ: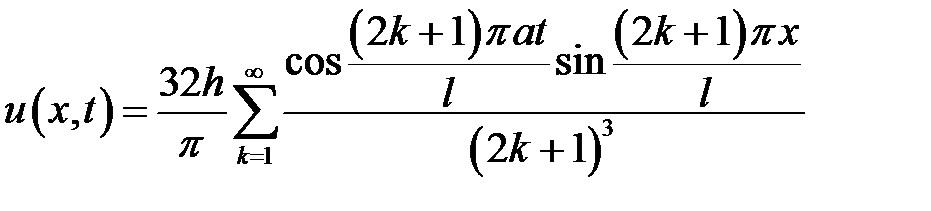 
, где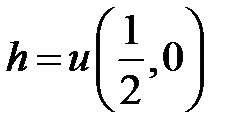 
.
33.3. Однородная струна, закрепленная на концах х = 0, х = l, имеющая в начальный момент времени форму
,
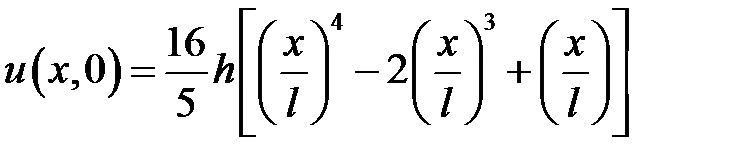где h> 0 — достаточно малое число, начала колебаться без начальной скорости. Найти свободные колебания струны.
Ответ: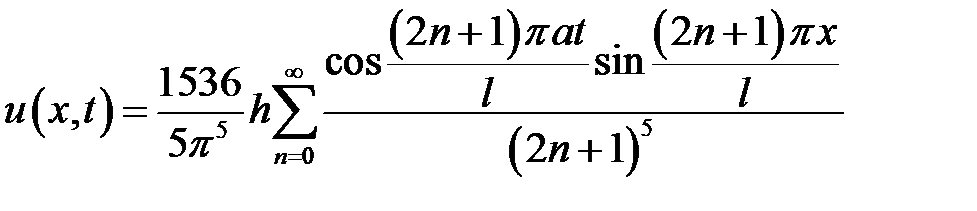 
.
33.4. Однородная струна длиной l натянута между точками х = 0 и х = l. В точке х = 0 струна оттягивается на небольшое расстояние h от положения равновесия и в момент времени t = 0 отпускается без начальной скорости. Определить отклонение u(x, t) струны для любого момента времени.
Ответ: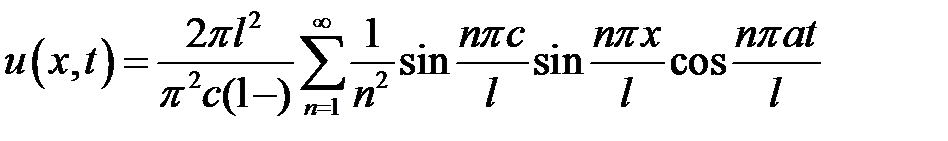 
.
33.5. Струна, закрепленная на концах х = 0 и х = l, в начальный момент имеет форму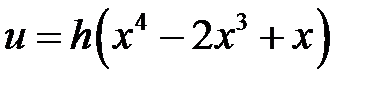 
. Найти форму струны для лю-бого момента времени t, если начальные скорости отсутствуют.
Ответ: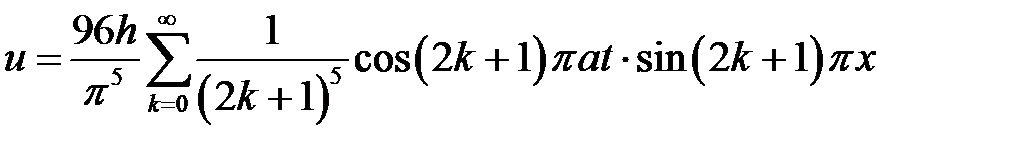 
.
33.6. Найти решение уравнения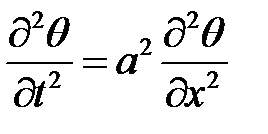 
, удовлетворяющее ус-ловию 
, 
, 
, 
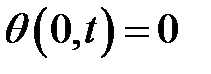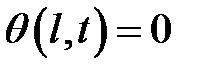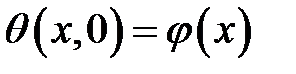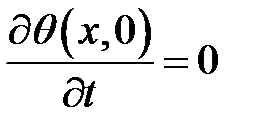, где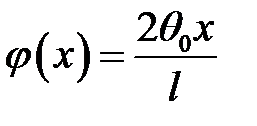 
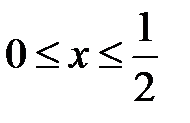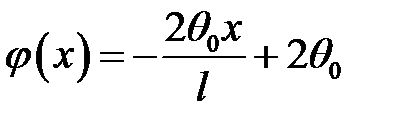при 
, 
при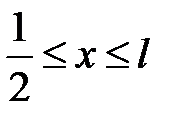 
.
Ответ: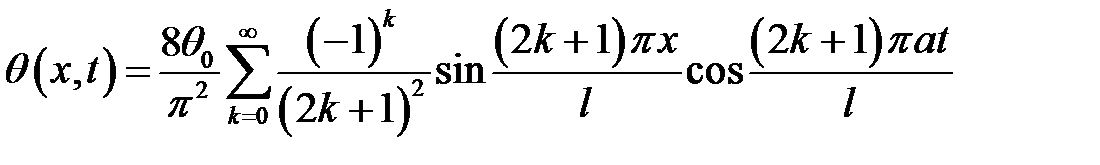 
.
33.7. Найти закон колебаний струны, начальная форма смещения которой на рисунке 33.2, а начальная скорость всех точек ее равна 0.
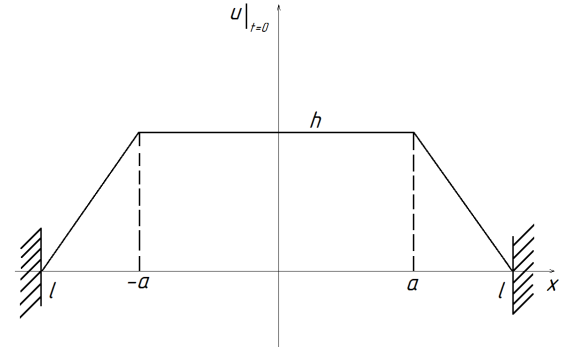
Рис.33.2
Ответ: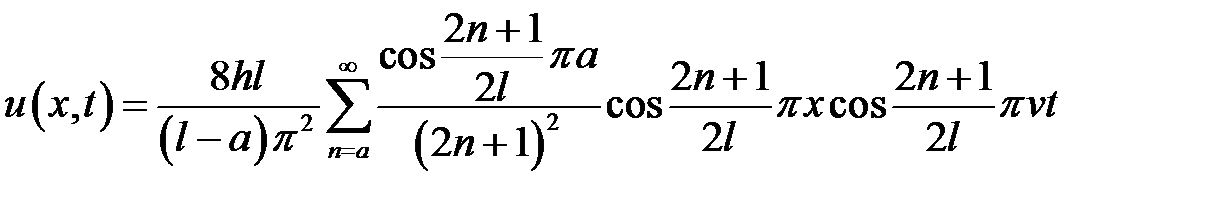 
.
33.8. Однородная струна длиной l закрепленная на обоих концах находится в прямолинейном положении равновесия. В некоторый мо-мент времени принимаемый за начальный, она получает в точке х = с удар от молоточка, который сообщает этой точке скорость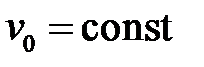 
. Найти отклонение u(x, t) струны для любого момента времени
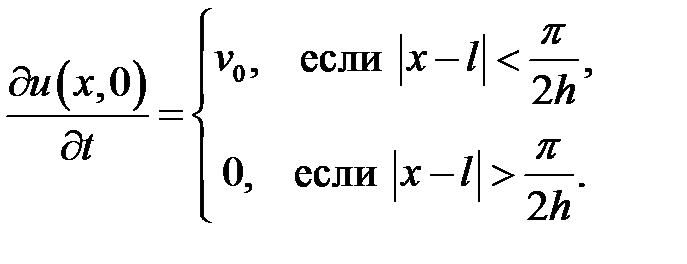
Ответ: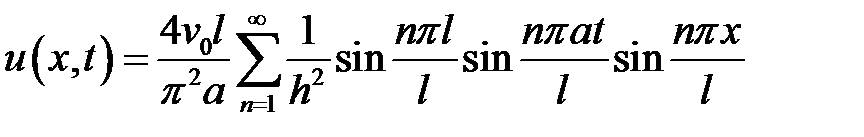 
.
33.9. Задача 2.7.
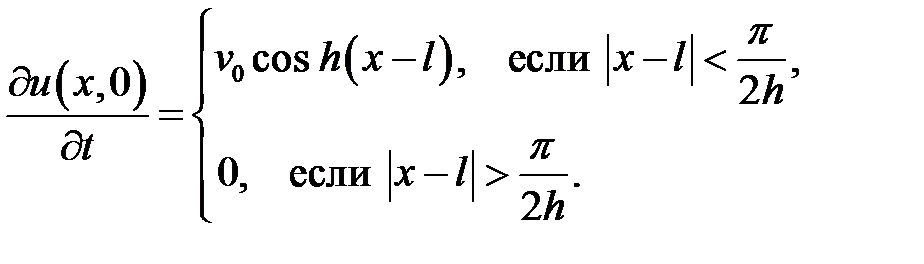
Ответ: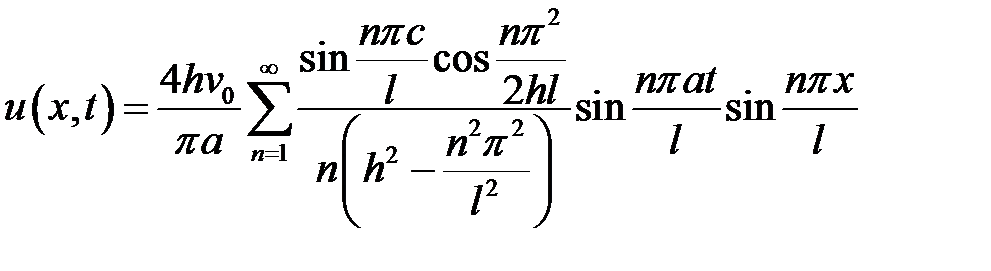 
.
33.10. Решить
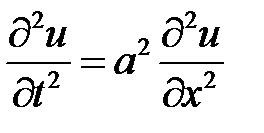
при условиях:
, 
, 
, 
.
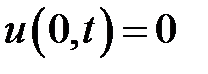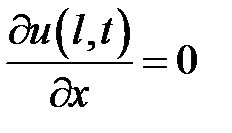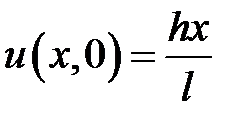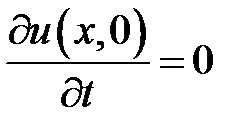Ответ: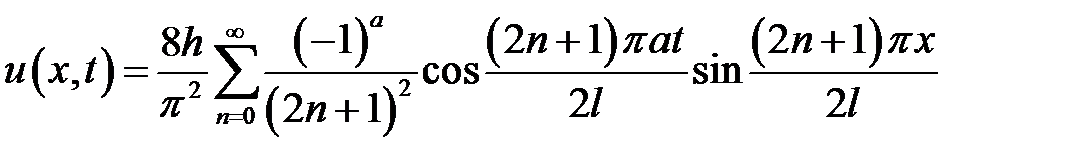 
.
33.11. Однородный стержень длиной 2l под действием сил, при-ложенных к его концам, укоротился на величину 2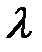 
. При t = 0 он освобожден от действующих внешних сил. Определить смещение u(x, t) сечения стержня с абсциссой х в момент t (средняя точка оси стержня имеет абсциссу х = 0).
Ответ: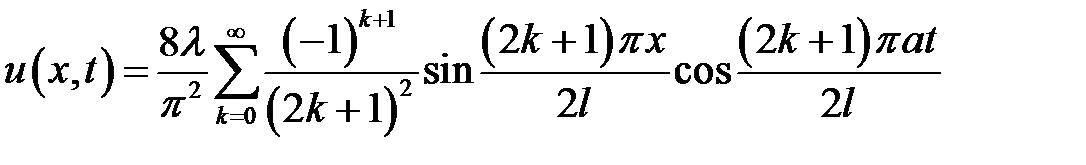 
.
33.12. Один конец стержня длины l закреплен, а на другой дей-ствует растягивающая сила P. Найти продольные колебания стержня, если при t = 0 сила P не действует.
Ответ: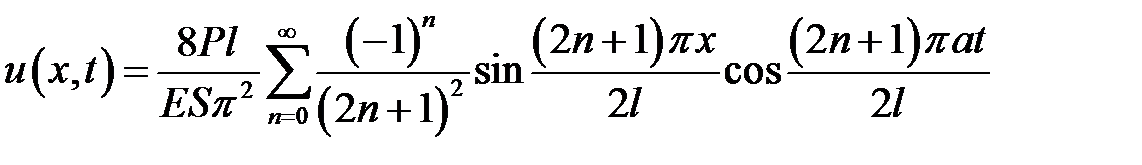 
,
где Е— модуль упругости материала,
S— площадь поперечного сечения стержня.
33.13. Решить
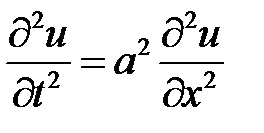
при условиях:
, 
, 
, 
.
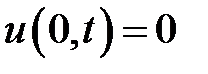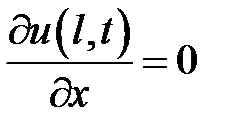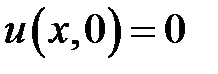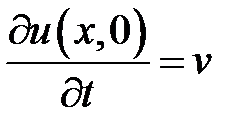Ответ: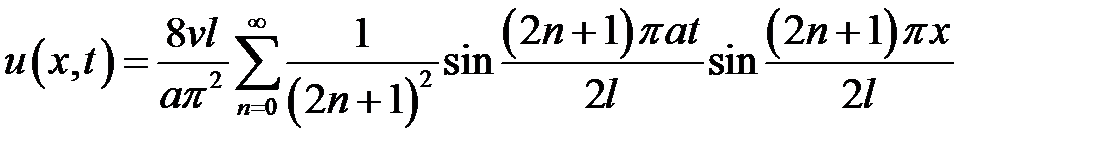 
.
33.14. Решить
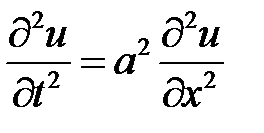
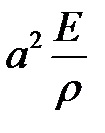
при условиях:
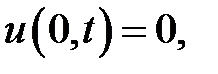
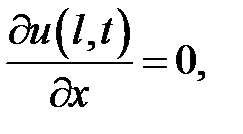
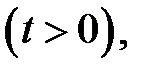
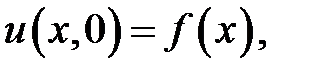
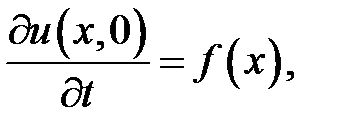
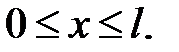
Ответ: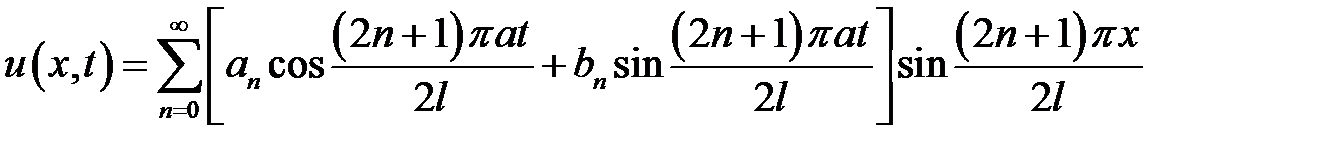 
,
где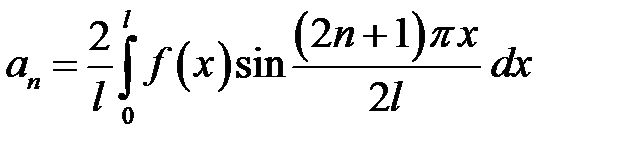 
,
.
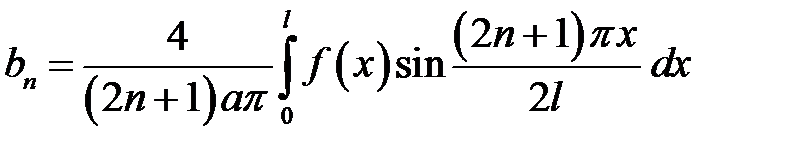33.15. Один конец стержня закреплен, а на второй действует сила Q. Найти продольные колебания стержня, если в начальный момент сила перестает действовать.
Ответ: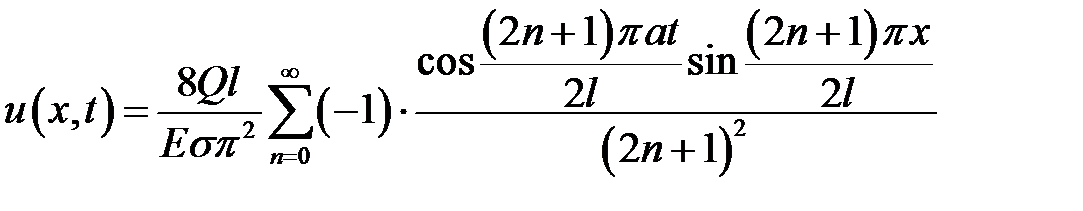 
,
где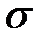 
— площадь поперечного сечения стержня.
33.16. Изучить свободные продольные колебания однородного ци-линдрического стержня длиной l, у которого оба конца свободны.
Ответ:
,
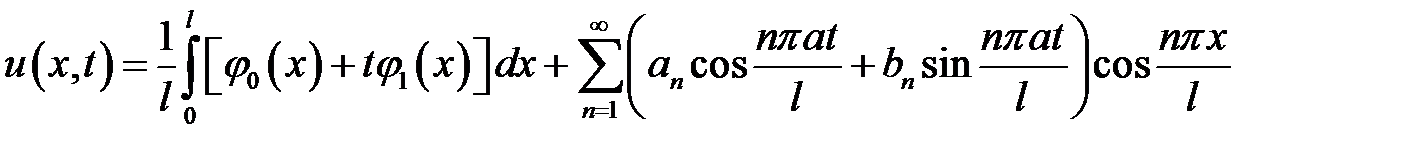где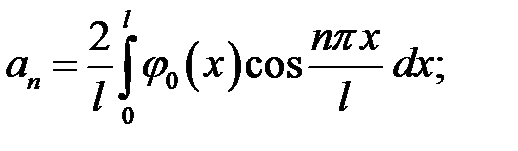 
.
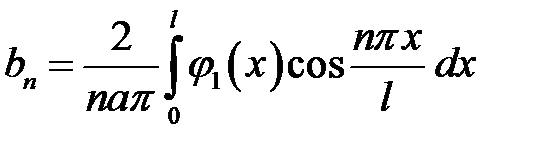Указание. Задача приводится к интегрированию уравнения:
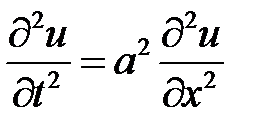
при условиях:
, 
, 
, 
, 
.
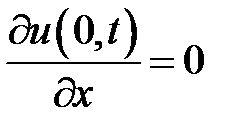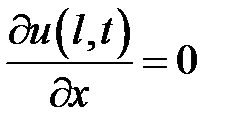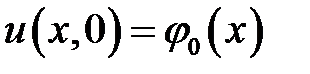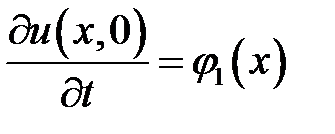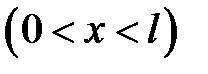33.17. Однородный стержень длиной 2l сжат силами, приложен-ными к его концам, так, что он укоротился до длины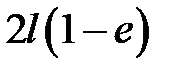 
. При t = 0 нагрузка снимается. Показать, что смещение u сечения с абсцис-сой х стержня определяется формулой:
,
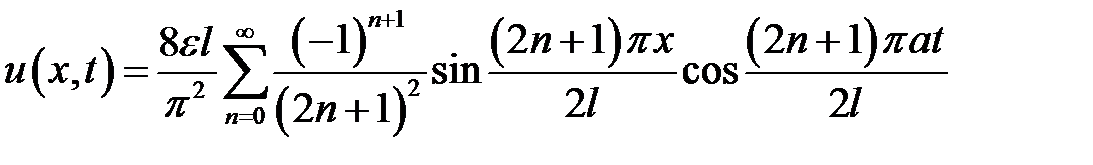если точка х = 0 находится по середине стержня и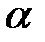 
— скорость продольных волн в стержне.
Указание. Проинтегрировать уравнение задачи 2.15 при усло-виях:
, 
, 
, 
.
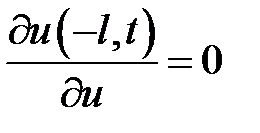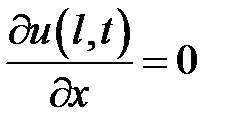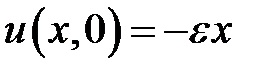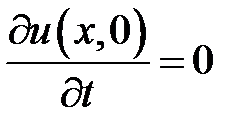33.18. Исследовать свободные колебания закрепленной струны, колеблющейся в среде, сопротивление которой пропорционально первой степени скорости.
Ответ: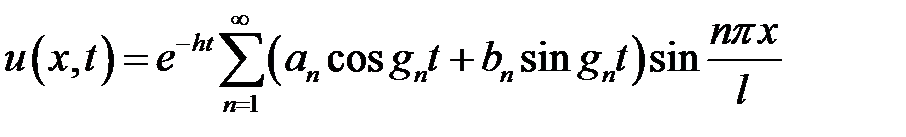 
,
где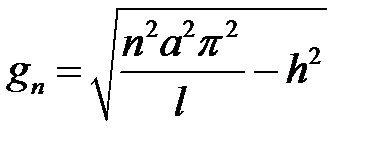 
,
,
.
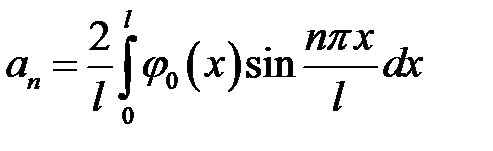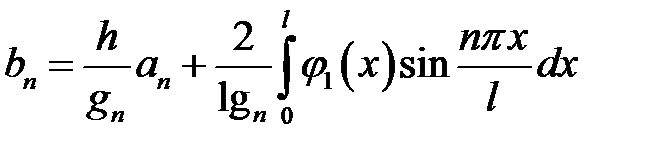Указание. Применить метод разделения переменных к интегрированию уравнения:
,
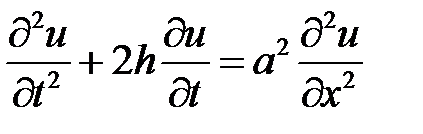где h – малое положительное число, при условиях:
, 
, 
, 
.
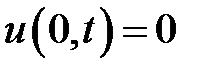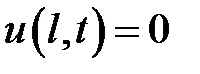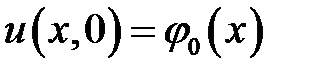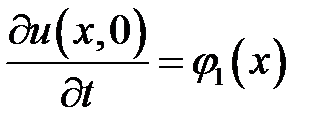33.19. Изучить вынужденные поперечные колебания струны, за-крепленной на концах х = 0 и подверженной на концах х = l действию возмущающей гармонической силы, вызывающей смещение, равное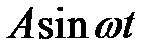 
.
Ответ: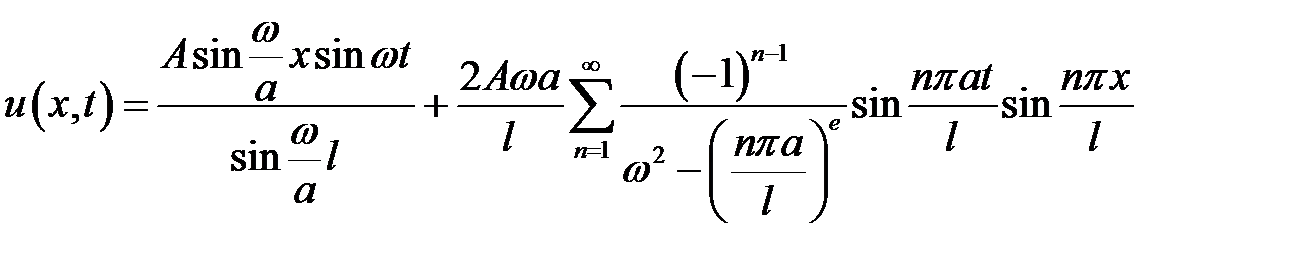 
.
Указание. Задача приводится к интегрированию уравнения:
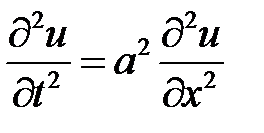(1)
при условиях:
, 
, 
, 
.
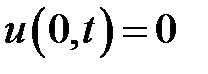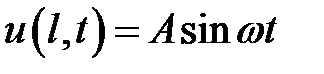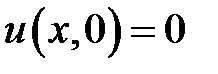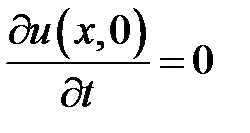Решение задачи следует искать в виде суммы u = v + w, где w— решение уравнения (1), удовлетворяющее краевым условиям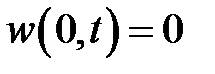 
, 
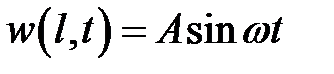, а v – решение уравнения (1) при условиях: 
, 
, 
, 
.
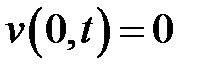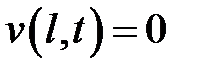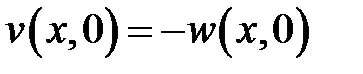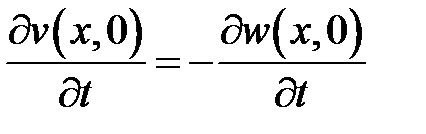33.20. Стержень длиной l, конец которого х = 0 закреплен, находится в состоянии покоя. В момент времени t = 0 к свободному концу приложена сила Q (на единицу площади), направленная вдоль стержня. Найти смещение u(x, t) стержня в любой момент времени t > 0.
Ответ: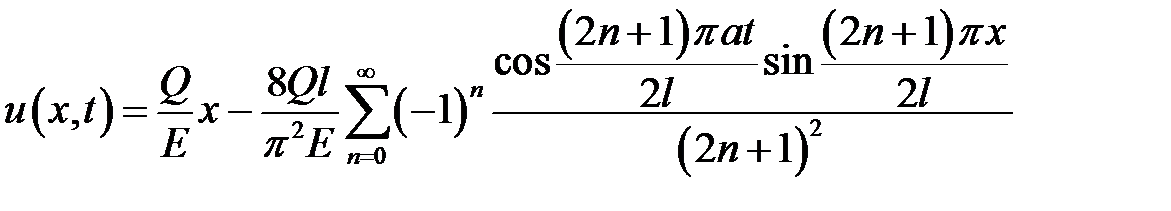 
.
Указание. Задача приводится к решению уравнения:
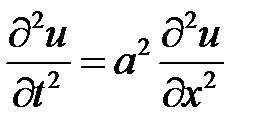
при условиях:
, 
, 
, 
.
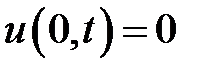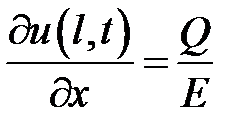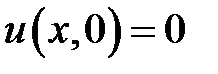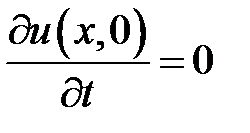См. также указания к задаче 2.18.
33.21. Изучить продольные колебания однородного цилиндри-ческого стержня, один конец которого заделан, а к другому концу приложена сила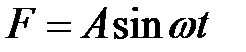 
, направление которой совпадает с осью стержня.
Ответ: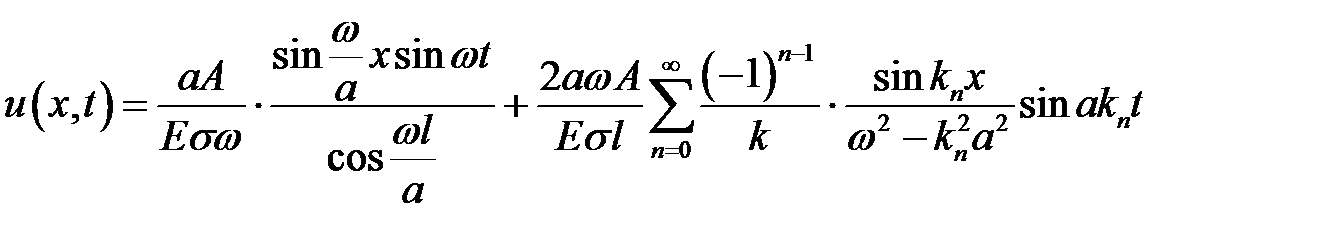 
,
где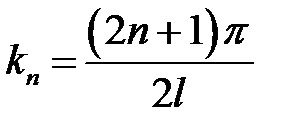 
, причем 
.
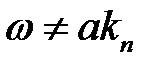Указание. Задача приводится к решению уравнения:
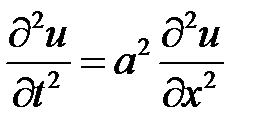
при условиях:
, 
, 
, 
.
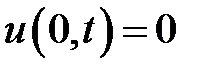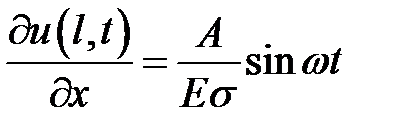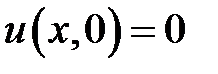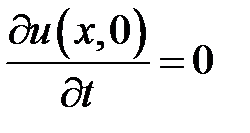См. также указание к задаче 2.18.
33.22. Стержень подвешен вертикально и защемлен так, что смещение во всех точках равно нулю. В момент времени t = 0 стержень освобождается, оставаясь закрепленным в верхней точке. Изучить вынужденные колебания стержня.
Ответ: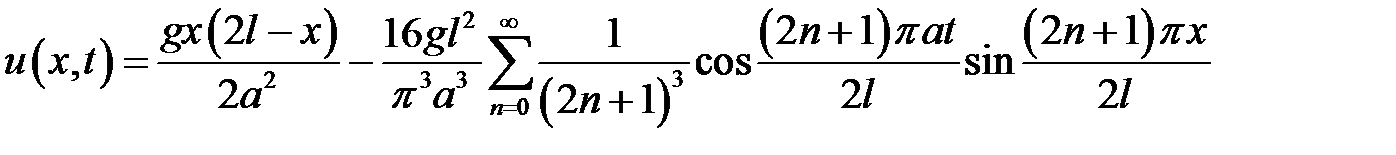 
,
где g – ускорение силы тяжести.
Указание. Задача приводится к интегрированию уравнения:
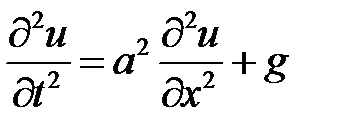(2)
при условиях:
, 
, 
, 
.
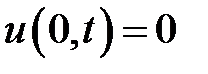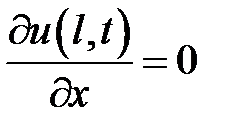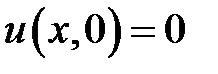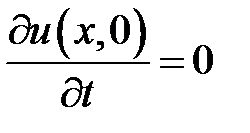Решение задачи следует искать в виде суммы u = v + w, где v есть решение неоднородного уравнения (2), удовлетворяющее крае-вым условиям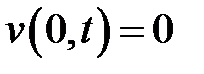 
, 
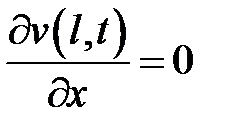, причем v следует искать в виде 
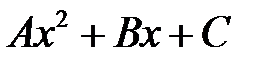, а w есть решение однородного уравнения при условиях: 
, 
, 
, 
.
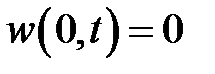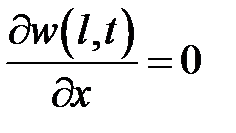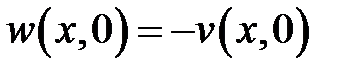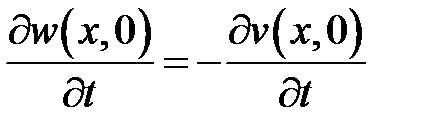33.23. Решить уравнение
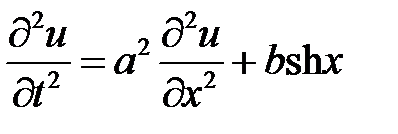
при нулевых начальных и краевых условиях:
, 
.
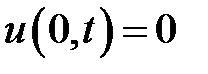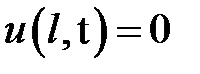Ответ: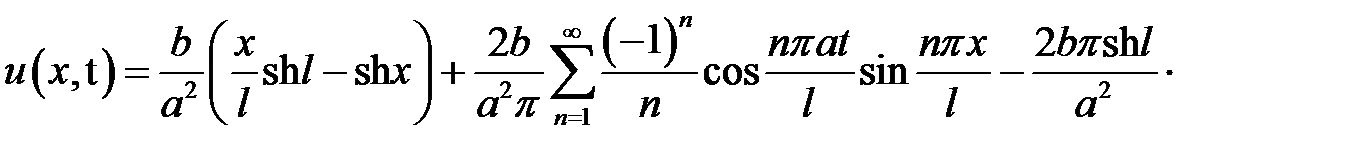 
.
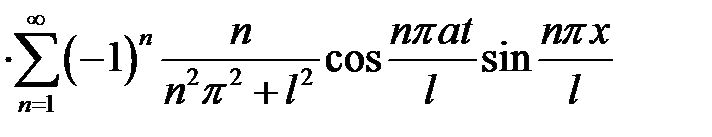Указание. Решение следует искать в виде суммы:
,
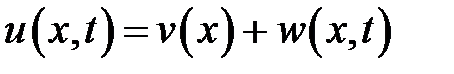где u(x) есть решение уравнения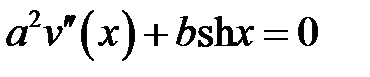 
, удовлетворяющее краевым условиям: 
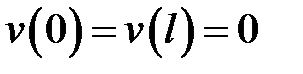, а w – решение уравнения 
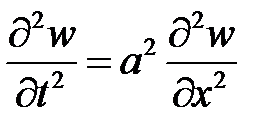при условиях: 
, 
, 
, 
.
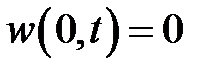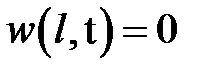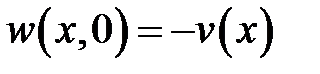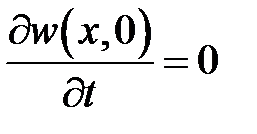33.24. Решить уравнение
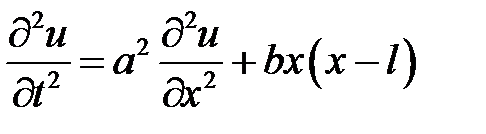
при нулевых начальных и краевых условиях: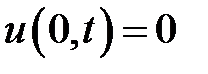 
, 
.
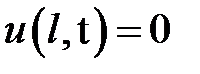Ответ: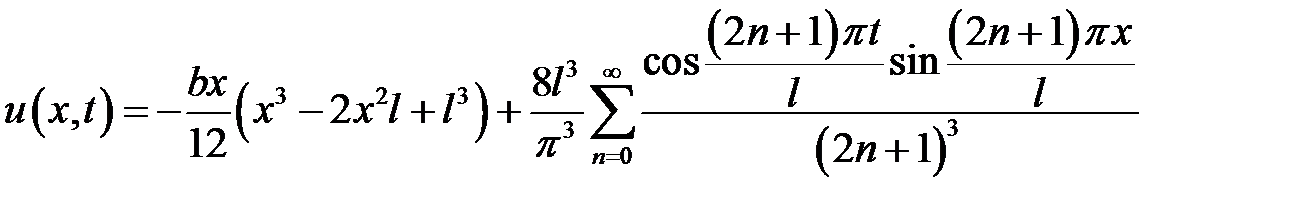 
.
33.25. Решить уравнение
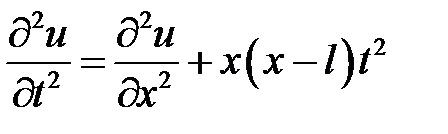
при нулевых начальных и краевых условиях: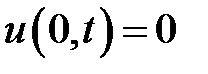 
, 
.
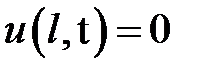Ответ:
.
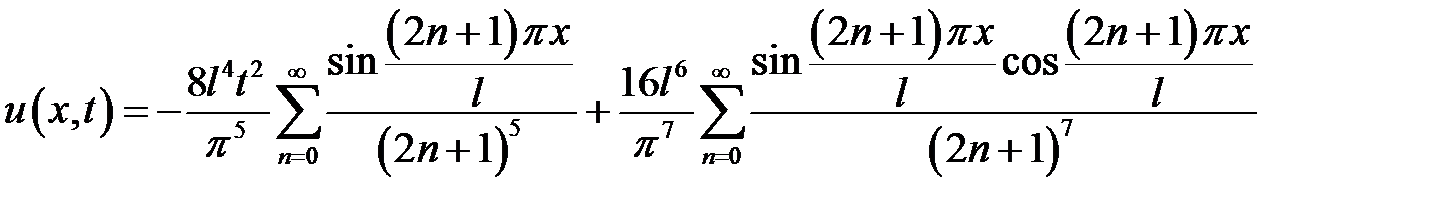33.26. Решить задачу о колебании струны 0 <x<l с закреплен-ными концами, если начальные скорости равны нулю, а начальное отклонение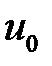 
имеет форму 
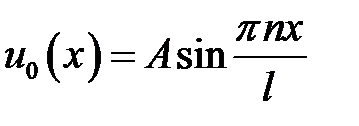, n— целое.
Ответ: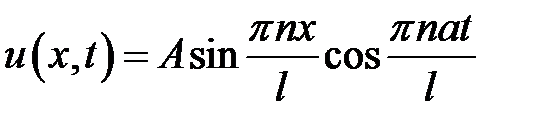 
.
33.27. Струна с закрепленными концами в t = 0 находится в покое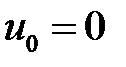 
. Начальная скорость 
, 
.
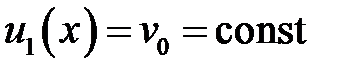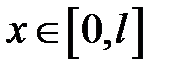Ответ: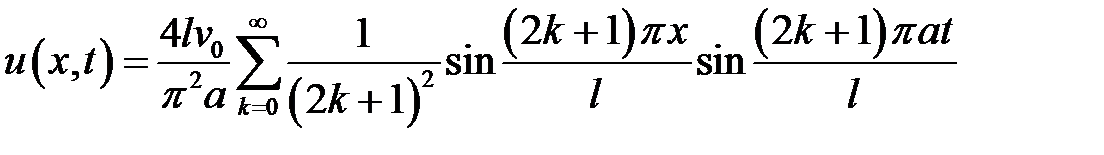 
.
33.28.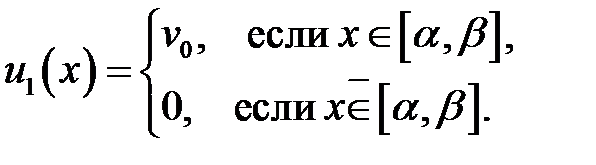 
Ответ: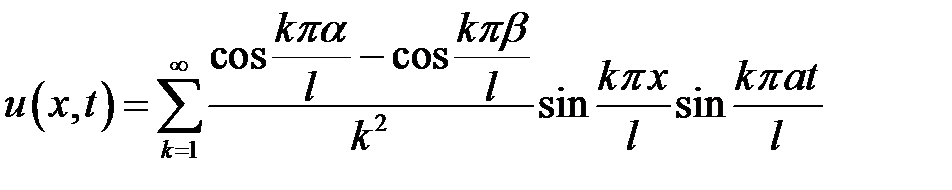 
.
33.29. Найти функцию, гармоническую в кольце 1 <r< 2, т. к.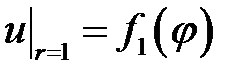 
, 
, 
, 
.
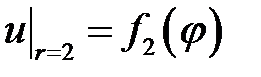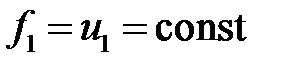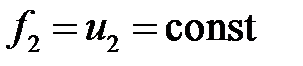Ответ: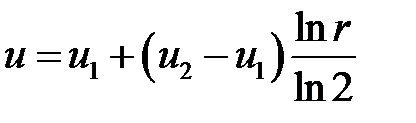 
.
33.30.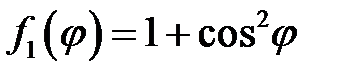 
, 
.
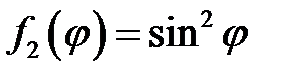Ответ: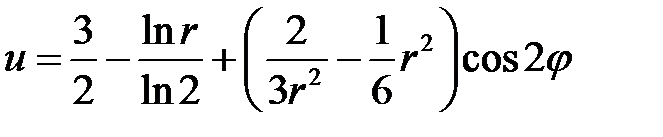 
.
33.31. Найти решение уравнения Лапласа для внутренней части кольца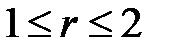 
, 
, 
.
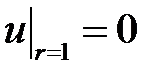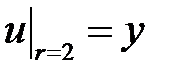Ответ: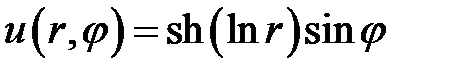 
.
Дата: 2018-09-13, просмотров: 2187.
