Возьмем однородный стержень длины l, теплоизолированный со всех сторон, кроме, быть может, своих концов, и достаточно тонкий, чтобы считать температуру на всей площади каждого поперечного сечения одинаковой. Если стержень нагрет неравномерно, то в нем будет происходить перенос тепловой энергии, и температура в сечениях будет меняться. Расположим стержень на участке 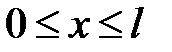 оси Ох. Пусть S(x) — площадь поперечного сечения, абсцисса которого равна х. Обозначим через U(x, t) температуру в сечении S(x) в момент времени t.

Теорема

Температура стержня U(x, t) в момент времени t в сечении, аб-сцисса которого равна х, описывается уравнением:

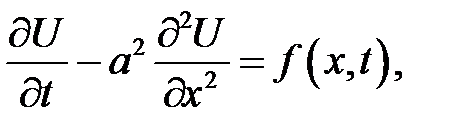                             (25.1)

где

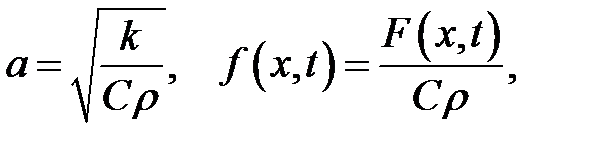
k— коэффициент теплопроводности, С— удельная теплоемкость, 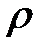— объемная плотность, F(x, t) — плотность тепловых источников.

Уравнение (25.1) называется уравнением теплопроводности стержня или уравнением линейной теплопроводности.

Доказательство.

Наша цель — составить уравнение баланса тепловой энергии 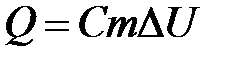— при получении тепла Q тело массы m и удельной теплоемкости С повышает свою температуру на 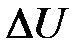. Выделим мысленно кусочек стержня (х, х + dx) (рис. 25.1). Тогда его масса будет равна:

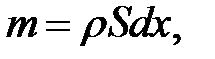                                       (25.2)

где 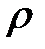— плотность, S— площадь сечения, Sdx— объем кусочка. Теперь займемся нахождением Q— количества тепла, получаемого нашим кусочком за время dt. Известно, что количество тепла Q(x, t), протекающее через сечение S(x) за время dt:

а) пропорционально промежутку времени dt,

б) пропорционально площади сечения S(x),

в) пропорционально разности температур, приходящейся на единицу длины 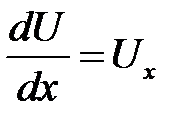. Следовательно, за время dt через S(x) прой-дет количество тепла:

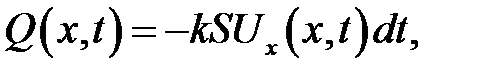                            (25.3)

где k— коэффициент теплопроводности, k > 0. Формула (25.3) называется законом Фурье. Знак минус объясняется тем, что тепло течет от горячих мест к холодным. Или, более подробно: если тем-пература сечений стержня увеличивается в направлении от левого конца к правому, то есть 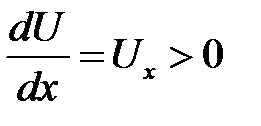, то тепловой поток будет на-правлен в обратную сторону, то есть Q< 0. В дальнейшем будем считать, что тепловой поток, проходящий сквозь наш кусочек, направлен в правую сторону. В этом случае получается, что через сечение S(x) тепло Q(x, t) входит в наш кусочек, а тепло Q(x + dx, t) через сечение S(x + dx) выходит. В общем случае количество тепла, вышедшее через S(x + dx), немного отличается от Q(x, t) и равно:

Q(x + dx, t) = Q(x, t) + dQ(x, t).

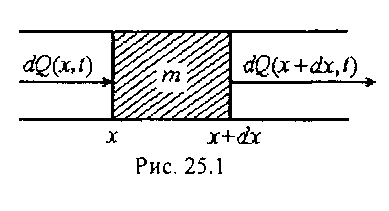
Рис. 25.1

Тогда внутри кусочка останется количество тепла:

Q(x, t) – Q(x + dx, t) = -dQ(x, t).

или

Если стержень однороден и все поперечные сечения одинаковы, то:

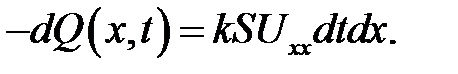
В дополнение к этому предположим, что внутри стержня порож-дается или поглощается тепло вследствие, например, химических реакций или из-за прохождения тока. Чтобы определить это тепло, введем функцию F(x, t) — количество тепла, выделяемое единицей объема за единицу времени. Эту функцию называют плотностью тепловых источников. Тогда за время dt в нашем кусочке объемом Sdx выделится дополнительное количество тепла FdtSdx, и суммарное количество тепла будет равно:

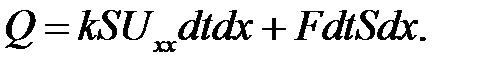                      (25.4)

Подставим (25.2) и (25.4) в уравнение теплового баланса. Полу-чим:

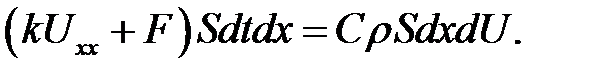                            (25.5)

Разделим на :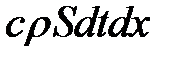

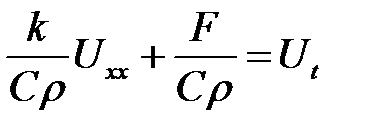
и введем обозначения:

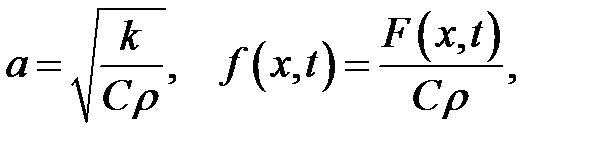
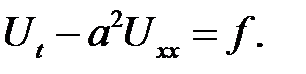
Теорема доказана.