Определение. Квадратичная форма 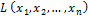 называ ется положительно (отрицательно) определённой, если на любом ненулевом наборе значений переменных она принимает положительное (отрицательное) значение.

Ясно, что для того, чтобы квадратичная форма была положительно (отрицательно) определённой, необходимо и достаточно, чтобы в её каноническом виде присутствовали квадраты всех её переменных и все коэффициенты при квадратах переменных были положительны (отрицательны).

Например, квадратичная форма 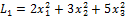 является положительно определённой, а форма  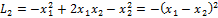- отрицательно определённой.

Теорема 1. Для того, чтобы квадратичная форма L = Х 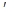АХ была положительно (отрицательно) определённой, необходимо и достаточно, чтобы все собственные значения 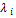матрицыА были положительны (отрицательны).

Приведение формы к каноническому виду – дело трудоёмкое, и, поэтому, сказанное выше малоэффективно.

Оказывается, можно провести анализ квадратичной формы на положительную (отрицательную) определённость, не приводя форму к каноническому виду. В ряде случаев для установления знакоопределённости квадратичной формы применяется критерий Сильвестра.

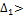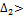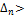Теорема 2 (критерий Сильвестра). Для того, чтобы квадратичная форма была положительно определённой, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е.  0,  0, …,  0, где

 = .

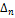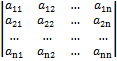Доказательство. Необходимость. Пусть 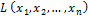 положительна определена. Тогда существует подстановка Х = СУ с невырожденной матрицейС, преобразующая форму в 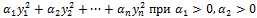, …, 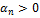.Тогда

и det 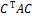 = |  | 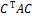= 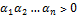. Но de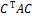t  = det 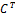detAdetC = detА 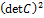. Следовательно, detА = 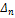˃ 0.

Теперь рассмотрим часть формы .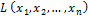

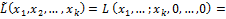
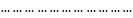
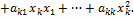
Эта форма, рассматриваемая как форма от 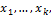 положительно определена, ибо её значения при не равных одновременно нулю  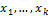суть значения формы  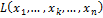при не равных одновременно нулю значениях для 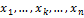. Поэтому

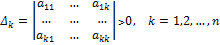 – 1.

Достаточность. Пусть  при 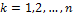. Тогда форма  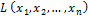может быть преобразована к каноническому виду посредством преобразования переменных с верхней квазитреугольной матрицей и каноническая форма будет равна

.

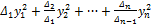Все коэффициенты при квадратах новых переменных положительны. Следовательно, форма положительно определена.

Теорема доказана.

Пример 8.Исследовать на знаковую определённость квадратичную форму

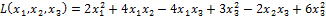Решение. Первый способ. Выпишем матрицу квадратичной формы:

А = .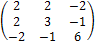

Для матрицы А характеристическое уравнение:

.

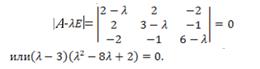Решая уравнение, находим 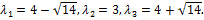 Так как корни характеристического уравнения матрицы А положительны, то на основании теоремы 1 квадратичная форма L – положительно определённая.

Второй способ. Так как главные миноры матрицы А

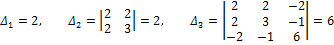
положительны, то по критерию Сильвестра данная квадратичная форма положительна определённая.

Для проверки приведём квадратичную форму к каноническому виду:

.

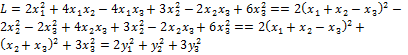Очевидно, что форма положительно определена, так как в её каноническом виде все коэффициенты положительны.

Канонический вид квадратичной формы не является однозначно определённым, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако, полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.

Теорема 3 (закон инерции квадратичных форм). Если квадратичная форма преобразована двумя способами к каноническому виду, то число квадратов новых переменных с положительными коэффициентами будет одинаково, так же как и число квадратов новых переменных с отрицательными коэффициентами. Другими словами, число положительных и отрицательных коэффициентов не зависит от способа приведения формы к каноническому виду.

Например, квадратичную форму 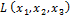 =  применив невырожденное линейное преобразование 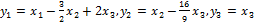 можно привести к виду  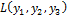= 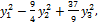а также применив невырожденное линейное преобразование

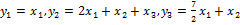 можно привести к виду

=

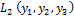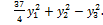
Как видно, число положительных и отрицательных коэффициентов сохранилось.

Контрольные вопросы к главе 5

1. Что называется квадратичной формой?

2. Что называется матрицей квадратичной формы?

3. Когда квадратичная форма L( 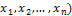 имеет канонический вид?

4. Сформулируйте теорему Лагранжа.

5. Что такое базис квадратичной формы?

6. Дайте классификацию квадратичных форм.

7. Сформулируйте закон инерции квадратичных форм.

ЗАКЛЮЧЕНИЕ

Учебное пособие предназначено для студентов экономических специальностей. Оно содержит необходимый подготовительный материал для прохождения курса «Математическое программирование».

Пособие состоит из пяти глав, содержит необходимый теоретический материал и соответствующие типовые примеры.

Читатель, желающий углубить свои знания в области систем линейных уравнений, может получить ответы на большинство вопросов, возникающих при практической реализации методов решения, в работах [1-13].

Список литературы

1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979.

2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 2000.

3. Боревич З.И. Определители и матрицы. – М.: Наука, 1988.

4. Высшая математика для экономистов: Учебник для вузов. Под редакцией Н.Ш. Кремера. – М.: ЮНИТИ - ДАНА, 2007.

5. Гусак А.А. Высшая математика. – Мн.: ТетраСистемс, 1998.

6. Данько П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1999.

7. Ефимов Н.В. Квадратичные формы. Матрицы. – М.: Наука, 1975.

8. Кострыкин А.И. Введение в алгебру. – М.: Наука, 1977.

9. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. – М.: Дело, 2003.

10. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1975.

11. Письменный Д.Т. Конспект лекций по высшей математике. – М.: Айрис Пресс, 2010.

12. Сборник задач по высшей математике для экономистов: Учебное пособие. Под редакцией В.И. Ермакова. – М.: ИНФРА-М, 2004.

13. Березина Н.А.Линейная алгебра. Конспект лекций, Ильин В.А., Позняк Э.Г. Линейная Алгебра. [Электронный ресурс] URL: http://mexalib.com/