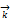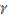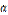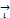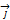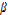|
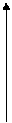 Рассмотрим в пространстве прямоугольную систему координатО
Рассмотрим в пространстве прямоугольную систему координатО 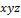 . Выделим на координатных осях O
. Выделим на координатных осях O 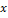 , Oy и Oz единичные векторы (орты), обозначаемые
, Oy и Oz единичные векторы (орты), обозначаемые 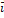 ,
, 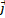 ,
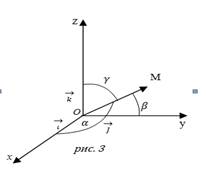
, 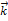 соответственно (см. рис. 3).
соответственно (см. рис. 3).
|
|
|

 Выберем произвольный вектор
Выберем произвольный вектор  =
= 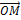 . Обозначим проекции вектора
. Обозначим проекции вектора  =
= 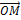 на оси O
на оси O 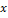 , Oy и Oz соответственно через
, Oy и Oz соответственно через 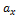 ,
,  и
и 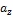 .
.
|
|



|
|
|
|
 =
= 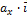 +
+  +
+  (3.2.1).
(3.2.1).
|
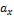 ,
,  и
и 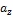 называются координатами вектора
называются координатами вектора  .
.
| |
 = (
= ( 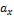 ;
;  ;
; 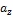 ).
).
На основе теоремы о длине диагонали прямоугольного параллелепипеда получаем
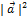 =
=  +
+  +
+ 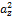 (3.2.2).
(3.2.2).
Отсюда получим
|  | =
| =  (3.2.3).
(3.2.3).
(3.2.3) – это формула для вычисления модуля (длины) вектора  =
= 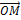 .
.
Пусть углы вектора  с осями O
с осями O 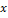 , Oy и Ozсоответственно равны α, β, γ. По свойству проекции вектора на ось, имеем
, Oy и Ozсоответственно равны α, β, γ. По свойству проекции вектора на ось, имеем
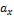 = |
= |  |
| 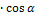 ,
,  = |
= |  |
| 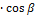 ,
, 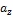 = |
= |  |
|  (3.2.4)
(3.2.4)
Из формул (3.2.4) вытекает, что
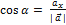 ,
,  ,
, 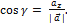
Числа 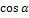 ,
, 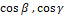 называются направляющими косинусами вектора
называются направляющими косинусами вектора 
Подставим выражения (3.2.4) в равенство (3.2.2), получаем
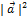 =
= 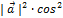 α +
α + 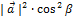 +
+ 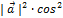 γ.
γ.
Сократив на 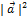 ≠ 0, получим соотношение
≠ 0, получим соотношение
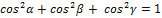 .
.
Заметим, что координатами единичного вектора  являются числа
являются числа 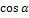 ,
, 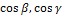 , т.е.
, т.е. 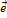 = (
= ( 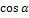 ;
;  ;
; 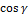 ).
).
Пусть 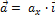 +
+ 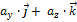 ,
, 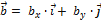 +
+ 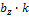 .
.
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можем записать:
1.  ±
±  =(
=( 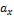 ±
±  +
+
+( 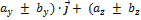 )
) 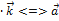 ±
±  = =(
= =( 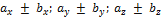 ).
).
Т.е. при сложении (вычитании) векторов их одноимённые координаты складываются (вычитаются).
2. 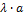 =
=  +
+ 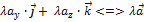 = =(
= =( 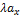 ;
; 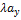 ;
; 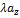 ). Т.е. при умножении вектора на число координаты вектора умножаются на это число.
). Т.е. при умножении вектора на число координаты вектора умножаются на это число.
Два вектора  и
и  равны (
равны ( 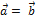 ) тогда и только тогда, когда выполняются равенства:
) тогда и только тогда, когда выполняются равенства: 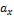 =
= 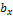 ,
,  =
= 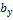 ;
; 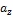 =
= 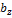 .
.
Выясним условия коллинеарности векторов  и
и  , заданных своими координатами.
, заданных своими координатами.
 ||
|| 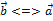 =
= 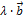 , где
, где 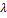 – некоторое число. Следовательно
– некоторое число. Следовательно
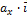 +
+  +
+  =
= 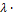 (
( 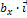 +
+ 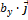 +
+  ) =
) = 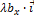 +
+ 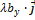 +
+ 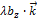 .
.
Отсюда получим
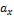 =
= 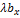 ,
,  =
= 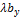 ,
, 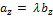 ,
,
т.е.
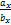 =
= 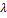 ,
, 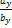 =
= 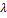 ,
,  =
= 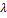 или
или 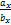 =
= 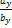 =
=  .
.
Таким образом, проекции коллинеарных векторов пропорциональны.
Найдём координаты вектора  =
= 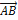 , если известны координаты точекА (
, если известны координаты точекА ( 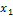 ,
, 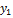 ,
, 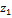 ) и В (
) и В ( 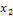 ,
,  ,
, 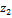 ). Имеем (см. рис. 4):
). Имеем (см. рис. 4):
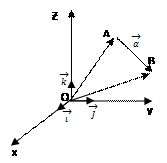
Рис. 4.
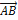 =
= 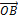 -
- 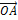 = (
= ( 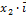 +
+  +
+ 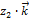 ) – (
) – ( 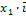 +
+ 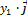 +
+ 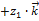 ) = (
) = ( 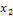 -
- 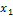 )
) 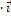 + (
+ (  -
- 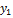 )
) 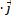 + (
+ ( 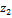 -
- 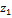 )
) 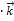
Следовательно: 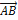 = (
= ( 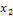 -
- 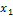 ;
;  -
- 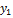 ;
; 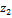 -
- 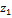 ).
).
|
Скалярным произведением двух ненулевых векторов  и
и  называется число, равное произведению их длин на косинус угла между ними.
называется число, равное произведению их длин на косинус угла между ними.
Скалярное произведение векторов  и
и  обозначается одним из символов
обозначается одним из символов  ,
, 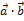 или
или 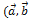 ):
):
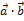 = |
= |  |
| 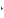 |
|  |
| 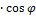 , (3.3.1)
, (3.3.1)
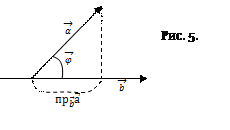 где
где  = (
= (  ).
).
Так как |  |
| 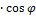 =
= 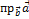 , (см. рис. 5),
, (см. рис. 5),
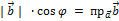 , то получаем:
, то получаем:
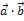 =|
=|  |
|  = =|
= =|  |
| 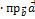 (3.3.2)
(3.3.2)
Свойства скалярного произведения:
1. 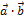 =
= 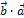 (свойство переместительности);
(свойство переместительности);
2. 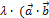 ) = (
) = ( 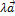 )
) 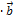 =
= 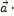 (
(  ) (свойство сочетательности);
) (свойство сочетательности);
3. 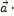 (
( 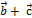 ) =
) = 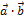 +
+  (свойство распределительности);
(свойство распределительности);
4. Скалярный квадрат вектора равен квадрату его длины: 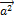 =
= 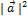 .В частности:
.В частности: 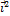 =
= 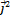 =
= 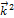 = 1.
= 1.
5. Если векторы 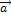 и
и 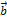 (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если
(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если 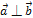 , то
, то 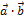 = 0. Справедливо и обратное утверждение: если
= 0. Справедливо и обратное утверждение: если 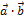 = 0 и
= 0 и 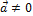 ,
, 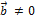 , то
, то 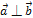 .
.
Пример 1. Найти длину вектора 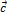 = 4
= 4  + 5
+ 5  , если |
, если |  | = 3, |
| = 3, | 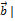 = 4, (
= 4, (  ) =
) =  .
.
Решение:
| 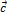 | =
| = 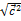 =
= 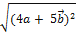 =
= 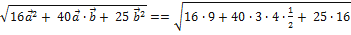 =
=  = 28
= 28
Векторы  и
и 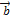 , скалярные произведения которых равно нулю, называются ортогональными.
, скалярные произведения которых равно нулю, называются ортогональными.
Если векторы  и
и 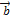 заданы своими координатами
заданы своими координатами  = (
= ( 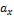 ;
;  ;
; 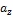 ),
),  = (
= ( 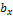 ;
; 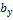 ;
; 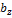 ), то
), то
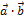 =
= 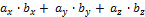 (3.3.3).
(3.3.3).
Формула (3.3.3) легко выводится из свойств скалярного произведения.
Пример 2.Показать,что четырёхугольник с вершинами А (-5; 3; 4), В (-1; -7; 5), С (6, -5, -3), D (2; 5; -4) есть квадрат.
Решение. Находим векторы.
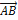 = (4; - 10; 1),
= (4; - 10; 1), 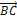 = (7; 2; -8),
= (7; 2; -8), 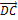 = (4; -10; 1),
= (4; -10; 1),  = (7; 2; -8).
= (7; 2; -8).
Сравнивая координаты этих векторов, заключаем, что
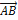 =
= 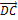 ,
, 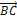 =
= 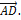
Так как
| 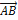 | =
| = 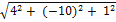 =
= 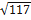 , |
, | 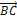 | =
| = 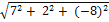 =
= 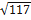 ,
,
то
| 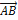 | = |
| = | 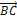 | = |
| = | 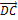 | = |
| = |  |.
|.
А поскольку
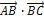 = 4
= 4 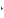 7 + (-10)
7 + (-10) 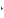 2 + 1
2 + 1 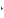 (-8) = 0,
(-8) = 0,
то 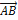 ^
^ 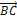
Следовательно, четырёхугольник ABCD есть квадрат.
Найдём проекцию вектора  на направление, заданное вектором
на направление, заданное вектором  . Из формул (3.3.2), (3.3.3), и (3.2.3) следует, что
. Из формул (3.3.2), (3.3.3), и (3.2.3) следует, что
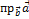 =
= 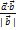 (
(  =
= 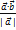 ), т.е.
), т.е. 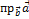 =
= 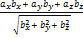 (3.3.4).
(3.3.4).
Пример 3. Даны векторы  = (3; -6; -1);
= (3; -6; -1);  = (1; 4; -5);
= (1; 4; -5); 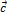 = (3; -4; 12).
= (3; -4; 12).
Найти  ,
, 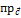 (
( 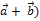 .
.
Решение. Применим формулу (3.3.4)
 =
=  =
= 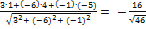

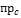 (
( 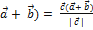 =
= 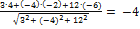 .
.
Дата: 2019-12-10, просмотров: 468.