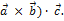Рассмотрим произведение векторов , составленное следующим образом: ( Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным произведением трёх векторов. Смешанное произведение представляет собой некоторое число.

Геометрически смешанное произведение интерпретируется как число, равное объёму параллелепипеда, построенного на векторах  как на ребрах. Смешанное произведение векторов положительно, если данные векторы образуют правую тройку, и отрицательно – если левую.

Свойства смешанного произведения:

1. 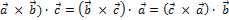, т.е. смешанное произведение не меняется при циклической перестановке векторов.

2. ( 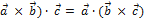, т.е. смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения. Замечание:это позволяет записывать смешанное произведение векторов ( в виде 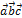 без знаков векторного, скалярного умножения.

3. 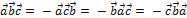, т.е. смешанное произведение меняет знак на противоположный при перемене мест любых двух векторов – сомножителей.

Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

4. Смешанное произведение ненулевых векторов 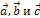 равны нулю тогда и только тогда, когда они компланарны.

Доказательство: если 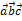 = 0, то  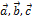- компланарны.

Допустим, что это не так. Можно было бы построить параллелепипед с объёмом V¹ 0. Но так как 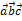 = ± V, то получили бы, что 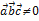. Это противоречит условию: .

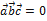Обратно, пусть векторы 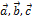 – компланарны. Тогда вектор  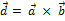будет перпендикулярен плоскости, в которой лежат векторы 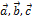, и следовательно, 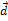^ 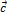. Поэтому 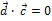, т.е.  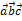= 0.

Пусть векторы 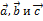 заданы своими координатами 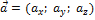, 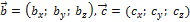. Найдём их смешанное произведение, используя формулу (3.4.2) и свойства скалярного произведения:

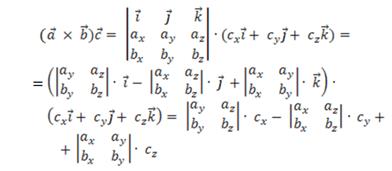
Воспользуясь свойствами определителей, полученную формулу можно записать и так:

(3.5.1).

Векторы  компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е. когда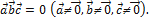

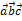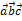Нетрудно показать, что объём параллелепипеда, построенного на векторах  вычисляется как V = ï ï, а объём треугольной пирамиды, построенной на этих же векторах равен V = ï ï.

Пример 5. Найти объём 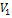 тетраэдра ABCD с вершинами в точках

А ( 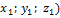, В ( , D ( .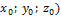

Решение. Найдём векторы трёх рёбер тетраэдра, исходящих из какой-либо его вершины, например вершины D:

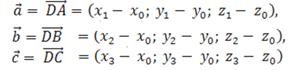
Построим параллелепипед на векторах 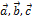, принимая за его основание параллелограмм, построенный на векторах  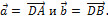За основание тетраэдра примем грань АВС. Площадь этой грани равна половине площади Sпараллелограмма :

Так как высота у параллелепипеда и тетраэдра одна и та же, то обозначив её через h, получим:

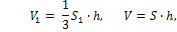
где V – объём параллелепипеда.

Из этих формул следует, что

Принимая во внимание формулу (3.5.1), получим

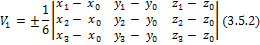
Пример 6. Показать, что точки А (3; -4; 1), В (2; -3; 7); С (1; -4; 3), D (4; -3; 5) лежат в одной плоскости.

Решение. Если точки

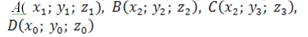
лежат в одной плоскости, то объём тетраэдра АВС D равен нулю. Из формулы (3.5.2) получаем необходимое и достаточное условие компланарности четырёх точек:

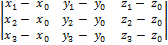 = 0.

Подставляя координаты точек А, В, С, D в определитель, стоящий в правой части формулы, получаем

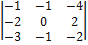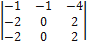= =  = 0.

Контрольные вопросы к главе 3

1. Дать определение скалярного произведения двух векторов.

2. Какие значения могут получиться в результате скалярного произведения?

3. Перечислите свойства скалярного произведения.

4. Чему равно скалярное произведение вектора самого на себя?

5. Как вычислить скалярное произведение, если векторы заданы своими координатами в ортонормированном базисе?

1. Сформулируйте необходимое и достаточное условие перпендикулярности двух векторов.

6. Как найти угол между векторами?

Тесты к главе 3

1.Чему равно скалярное произведение двух векторов, если длина первого равна 1, длина второго – 2, а угол между векторами — 60⁰?

a) 1;

b) 2;

с) 0.5.

2. Скалярное произведение двух векторов равно 0. Чему равен угол между векторами, еслидлина первого вектора -7, а второго -9?

a) 63;

b) 0⁰;

с) 90⁰.

3. Длина вектора равна 3 см. Чему равен скалярный квадрат вектора ?

a) 1;

b) 3;

с) 9.

4. Чему равно скалярное произведение двух векторов, если координаты первого {2; 1}, а координаты второго{1; 2} ?

a) 0;

b) 6;

с) 4.

5. Перпендикулярны ли два вектора, если координаты первого – {4; 2}, а координаты второго {-2; 4}?

a) нет;

b) да;

с) недостаточно данных.