Пусть  – линейное (векторное) пространство. Введём в данном пространстве метрику, т.е. способ измерять длины и углы. С этой целью введём понятие скалярного произведения.

Определение. Скалярным произведением двух векторов

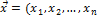) и 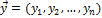 называется число

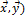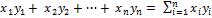(  = (4.4.1)

Скалярное произведение имеет следующие свойства:

1. (

2. (

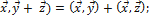
3. ( 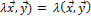 для любого действительного числа ;

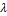4. ( 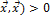, если 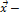ненулевой вектор; ( 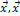) = 0, если  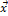– нулевой вектор.

Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным свойствам, называется евклидовым пространством.

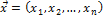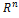Длина (норма) вектора в  определяется так:

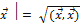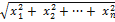⃒  = (4.4.2)

Длина (норма) вектора  обладает следующими свойствами:

1. 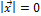 тогда и только тогда, когда ;

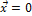2. , где ;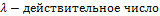

3. 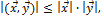(неравенство Коши – Буняковского);

4. 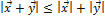, (неравенство треугольника).

Угол 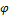 между двумя векторами  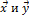определяется равенством

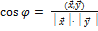,где 0 ≤ < .

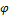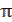Два вектора называются ортогональными, если их скалярное произведение равно нулю. Нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен .

Базис (или вообще система векторов) 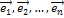n-мерного евклидова пространства называется ортонормированным, если

( .

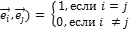Процессом ортогонализации системы векторов 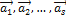 называется переход от этой системы к новой системе 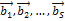, построенной следующим образом: 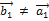;  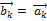-  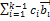(k = 2, 3, …, s), где  =  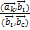(i = 1, 2, …, k – 1), есл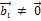и , и  – любое число.

Пример 4. В четырёхмерном пространстве дан базис 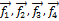. С помощью векторов этого базиса построить ортонормированный базис того же пространства.

Решение. Сначала построим в заданном пространстве какой-нибудь ортогональный базис .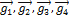

Положим 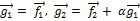. Подберём действительное число  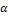так, чтобы выполнялось условие 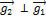. Умножив скалярное на  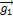обе части последнего равенства, получим

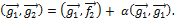
Так как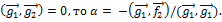

Далее, в равенстве 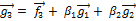 подберём  и 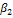 так, чтобы выполнялись условия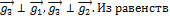

.

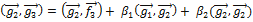Получим

= - ( .

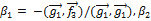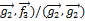Наконец, из равенства

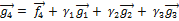 находим , .

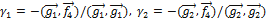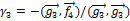Итак, при сделанном выборе α, , , 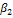, , 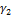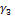векторы 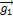, , 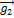,  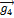попарно ортогональны. Значит, векторы

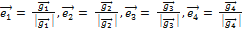 образуют ортонормированный базис.

Справедлива следующая теорема.

Теорема. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

Примером ортонормированного базиса является система n единичных векторов

Определение. Ортогональным дополнением подпространства L пространства 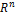называется совокупность  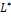всех векторов , каждый из которых ортогонален ко всем векторам из L.

Можно доказать, что:

a) 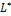является линейным подпространством пространства

б) сумма размерностей Lи 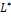 равна n;

в) пространство  есть прямая сумма подпространств L и 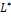, т.е.  = L .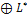

Пример 5. Построить ортогональный базис ортогонального дополнения 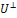 подпространства .

Решение. Приведём матрицу к ступенчатому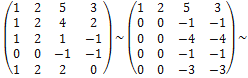

.

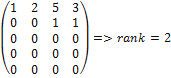Пусть 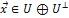=> 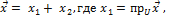dimV=4;

U = < 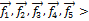 = < 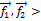, –линейно независимы; следовательно dimU = 2, 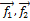– базис подпространства U может быть дополнен до базиса V векторами .

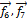V = U 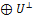,  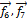– базис подпространства .

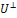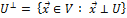, т.е. (  = 0. Пусть .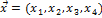

Тогда

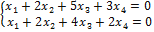
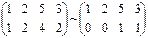
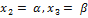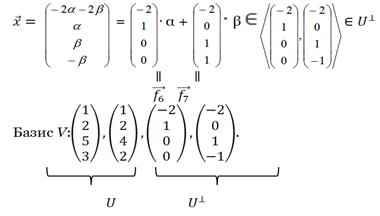
Пусть ; Тогда 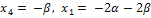. Следовательно