Отметим, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Пример 4. Квадратичная форма.
L( 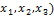 = 7
= 7 
после преобразования
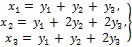
перейдёт в форму с матрицей
С 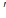 АС=
АС= 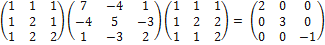 ,
,
т.е. в форму 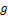 (
( 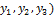 = 2
= 2 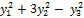 , которая имеет диагональную матрицу.
, которая имеет диагональную матрицу.
Определение. Квадратичная форма L( 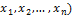 имеет канонический вид, если матрица квадратичной формы диагональна, т.е. в записи квадратичной формы отсутствуют произведения разных переменных:
имеет канонический вид, если матрица квадратичной формы диагональна, т.е. в записи квадратичной формы отсутствуют произведения разных переменных:
L( 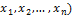 = =
= = 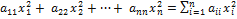
Теорема(теорема Лагранжа). Любая квадратичная форма при помощи невырожденного линейного преобразования переменных может быть приведена к каноническому (диагональному) виду.
Сформулируем предварительно два вспомогательных утверждения.
Лемма 1. Произведение двух (или нескольких) последовательно выполненных невырожденных линейных преобразований переменных является также невырожденным преобразованием.
Доказательство. Действительно, невырожденность преобразований Х = СУ и У = DZ означает, что матрицы С и D невырожденные. Но тогда матрица CD, т.е. матрица линейного преобразования Х = С(DZ) = (CD)Z, также невырожденная.
Лемма 2. Если у квадратичной формы (5.1.2) имеется хотя бы один ненулевой коэффициент, то надлежащим невырожденным линейным преобразованиям переменных Х = СУ она может быть преобразована в форму, у которой коэффициент при 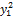 отличен от нуля.
отличен от нуля.
Доказательство. 1) Пусть 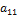 ≠ 0. В этом случае сама форма L обладает требуемым свойством и никакого преобразования делать не надо (можно сделать тождественное преобразование).
≠ 0. В этом случае сама форма L обладает требуемым свойством и никакого преобразования делать не надо (можно сделать тождественное преобразование).
2) Предположим, что 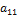 = 0, но при некотором
= 0, но при некотором 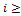 2 отличен от нуля коэффициент при
2 отличен от нуля коэффициент при  , т.е.
, т.е. 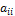 ≠ 0. В этом случае достаточно изменить нумерацию переменных, т.е. сделать преобразование вида
≠ 0. В этом случае достаточно изменить нумерацию переменных, т.е. сделать преобразование вида

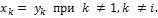
Это преобразование невырожденное (здесь легко усматривается обратное преобразование), и после его выполнения получим
L = … + 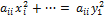 +…
+…
Выписанный член 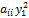 не имеет себе подобных, а потому он сократиться не может. Таким образом, поскольку
не имеет себе подобных, а потому он сократиться не может. Таким образом, поскольку 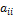 ≠ 0, для рассматриваемого случая лемма доказана.
≠ 0, для рассматриваемого случая лемма доказана.
3) Остаётся рассмотреть случай, когда 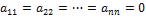 , т.е. когда все диагональные коэффициенты равны нулю. По условию форма имеет хоть один ненулевой коэффициент. Пусть
, т.е. когда все диагональные коэффициенты равны нулю. По условию форма имеет хоть один ненулевой коэффициент. Пусть 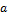 ij ≠ 0 (
ij ≠ 0 ( 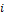 ≠j). Чтобы свести рассматриваемый случай к случаю 2, нам достаточно сделать какое-нибудь невырожденное преобразование, только бы появился квадрат одной из переменных с ненулевым коэффициентом. Сделаем, например, преобразование
≠j). Чтобы свести рассматриваемый случай к случаю 2, нам достаточно сделать какое-нибудь невырожденное преобразование, только бы появился квадрат одной из переменных с ненулевым коэффициентом. Сделаем, например, преобразование
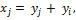

(в частности, 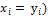 . Преобразование, видно, что невырожденное (обратным для него будет преобразование
. Преобразование, видно, что невырожденное (обратным для него будет преобразование 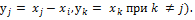 После выполнения преобразования получим
После выполнения преобразования получим
L = … + 2 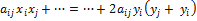 +
+
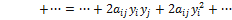
Член  является здесь единственным членом с
является здесь единственным членом с 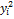 , поэтому после приведения подобных членов он не сократится. Полученная нами форма содержит, таким образом, квадрат переменной с ненулевым коэффициентом (
, поэтому после приведения подобных членов он не сократится. Полученная нами форма содержит, таким образом, квадрат переменной с ненулевым коэффициентом (  ≠ 0), и значит к ней применимо рассуждение пункта 2. Для завершения доказательства леммы 2 остаётся сослаться на лемму 1.
≠ 0), и значит к ней применимо рассуждение пункта 2. Для завершения доказательства леммы 2 остаётся сослаться на лемму 1.
А теперь переходим к доказательству теоремы Лагранжа.
Доказательство теоремы проведём индукцией по числу переменных 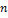 . При
. При 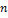 = 1 утверждение теоремы справедливо тривиальным образом: всякая квадратичная форма от одной переменной имеет вид
= 1 утверждение теоремы справедливо тривиальным образом: всякая квадратичная форма от одной переменной имеет вид 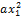 и является, следовательно, диагональной (всякая матрица 1-го порядка диагональна).
и является, следовательно, диагональной (всякая матрица 1-го порядка диагональна).
Предположим теперь, что 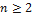 и что для форм от
и что для форм от 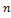 -1 переменных теорема уже доказана. Пусть L
-1 переменных теорема уже доказана. Пусть L 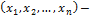 квадратичная форма от
квадратичная форма от 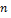 переменных. Если все коэффициенты формы – нули, то доказывать нечего (сама форма уже диагональна с нулевыми коэффициентами при квадратах). Пусть не все её коэффициенты нули. Если
переменных. Если все коэффициенты формы – нули, то доказывать нечего (сама форма уже диагональна с нулевыми коэффициентами при квадратах). Пусть не все её коэффициенты нули. Если  то согласно лемме 2 можно совершить невырожденное линейное преобразование переменных так, чтобы после преобразования формы коэффициент при квадрате первой переменной был отличен от нуля. Можно считать поэтому, что уже с самого начала
то согласно лемме 2 можно совершить невырожденное линейное преобразование переменных так, чтобы после преобразования формы коэффициент при квадрате первой переменной был отличен от нуля. Можно считать поэтому, что уже с самого начала 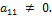
Выделим в форме (5.1.2) все члены содержащие  :
:


Здесь 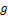 является формой от
является формой от  Преобразуем теперь выписанную сумму так, чтобы все члены с
Преобразуем теперь выписанную сумму так, чтобы все члены с  вошли в квадрат линейного выражения:
вошли в квадрат линейного выражения: 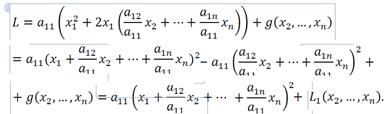
Здесь 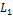 , как и
, как и 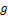 является квадратичной формой от
является квадратичной формой от 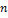 -1 переменных
-1 переменных 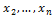 .
.
Сделаем преобразование переменных
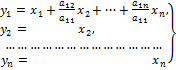 (5.2.1).
(5.2.1).
Преобразование (5.2.1) невырожденное. В нём новые переменные выражены через старые. Найдём для (5.2.1) обратное преобразование:
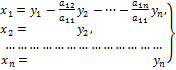 (5.2.2).
(5.2.2).
После выполнения преобразования (5.2.1) квадратичная форма примет вид:

По индуктивному предположению существует невырожденное линейное преобразование
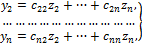 ,
,
при котором форма 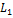 приводится к диагональному (каноническому) виду
приводится к диагональному (каноническому) виду
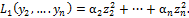
Для исходной формы Lвслед за преобразованием (5.2.2) выполнили следующее преобразование переменных:
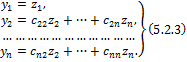 .
.
Определитель этого преобразования
 =
=  ≠ 0,
≠ 0,
следовательно, преобразование (5.2.3) невырожденное. После его выполнения вслед за преобразованием (5.2.2) форма L приобретает вид:

Таким образом, после выполнения двух невырожденных линейных преобразований форма L приняла диагональный (канонический вид). Теорема доказана.
Пример 5. Привести к каноническому виду квадратичную форму
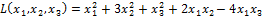 .
.
Решение. Имеем
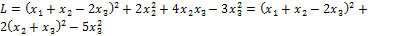 .
.
Следовательно, при помощи преобразования
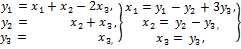
форма приводится к виду
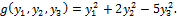
А теперь приведём пример приведения к каноническому виду квадратичной формы в случае, когда все диагональные коэффициенты равны нулю.
Пример 6. Привести форму 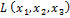 = 2
= 2 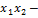 6
6 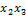 + 2
+ 2  к каноническому виду. Найти матрицу перехода от исходного базиса к базису, в котором форма имеет канонический вид.
к каноническому виду. Найти матрицу перехода от исходного базиса к базису, в котором форма имеет канонический вид.
Решение. Так как в форме нет членов с квадратом переменной, то делаем вспомогательное преобразование с целью получить квадрат:
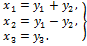 .
.
Получаем

Выполним то же самое в матричном виде
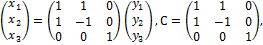
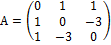
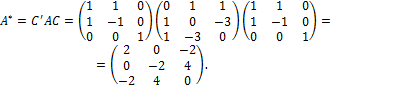
Теперь выделим полный квадрат при переменной 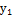 .
.
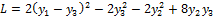 .
.
Заменим переменные по формулам

Получаем

Выполним переход от переменных 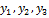 к переменным
к переменным  в матричном виде
в матричном виде
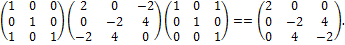
Теперь выделим полный квадрат при переменной  .
.

Введём переменные
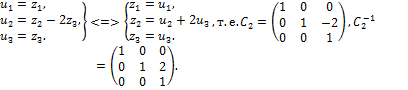
Имеем
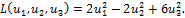
Это – форма канонического вида.
Выполним последний шаг в матричном виде:
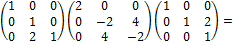
 .
.
А теперь найдём искомую матрицу:
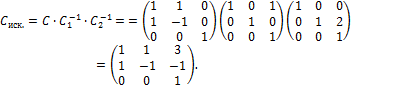
Проверка:
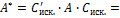
 .
.
В упрощении квадратичной формы от канонического вида можно пойти дальше – к нормальному виду. Нормальным видом называется такой канонический вид квадратичной формы, в котором коэффициенты при квадратах неизвестных (переменных) равны  1.
1.
Справедлива следующая теорема.
Теорема. Для любой квадратичной формы существует базис, в котором она имеет нормальный вид.
Пример 7. Продолжим пример 6 и приведём форму к нормальному виду.
Решение. Достаточно перейти от последнего базиса к новому, положив

Дата: 2019-12-10, просмотров: 322.