Определение. Пусть 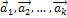 – векторы линейного пространства
– векторы линейного пространства  ,
, 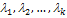 - скаляры. Вектор
- скаляры. Вектор
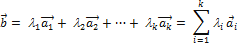
называется линейной комбинацией векторов 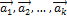 .
.
Определение. Множество всех линейных комбинаций векторов 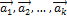 называется линейной оболочкой системы векторов
называется линейной оболочкой системы векторов 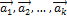 и обозначается символом <
и обозначается символом < 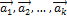 >.
>.
Можно также определить линейную оболочку любого подмножества S 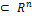 , принимаяпод <S> пересечение всех подпространств, содержащих данное множество S векторов из
, принимаяпод <S> пересечение всех подпространств, содержащих данное множество S векторов из  .
.
Теорема 1.Пусть  – линейное пространство и
– линейное пространство и 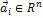 , i = 1, 2, …, k. Линейная оболочка <
, i = 1, 2, …, k. Линейная оболочка < 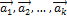 > является линейным подпространством пространства
> является линейным подпространством пространства  .
.
Доказательство. Пусть 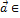 <
< 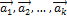 > и
> и  . Покажем, что
. Покажем, что 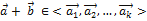 и l
и l 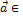 <
< 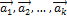 >.
>.
Действительно,
 ,
,
тогда
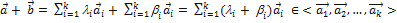 и
и
 ,
,
что и требовалось доказать.
Определение. Система векторов 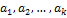 называется линейно зависимой, если среди векторов системы существует вектор, являющийся линейной комбинацией остальных.
называется линейно зависимой, если среди векторов системы существует вектор, являющийся линейной комбинацией остальных.
Существует также эквивалентное определение линейной зависимости векторов.
Определение. Система векторов  называется линейно зависимой, если найдётся набор чисел
называется линейно зависимой, если найдётся набор чисел 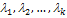 , не все из которых равны нулю, такой, что выполняется равенство
, не все из которых равны нулю, такой, что выполняется равенство
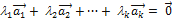 . (4.2.1)
. (4.2.1)
В противном случае система 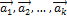 называется линейно независимой.
называется линейно независимой.
Из приведённых выше определений следует, что векторы  линейно независимы, если равенство (4.2.1) справедливо лишь при
линейно независимы, если равенство (4.2.1) справедливо лишь при  , и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел
, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 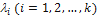 отлично от нуля.
отлично от нуля.
Примером линейно независимых векторов являются два неколлинеарных вектора 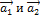 на плоскости. Действительно, условие (4.2.1)
на плоскости. Действительно, условие (4.2.1) 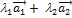 =
= 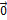 будет выполняться лишь в случае, когда
будет выполняться лишь в случае, когда 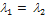 , ибо если, например,
, ибо если, например, 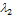 ¹ 0, то
¹ 0, то 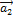 =
= 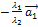 и векторы
и векторы 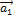 и
и 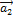 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
коллинеарны. Однако любые три вектора плоскости линейно зависимы.
Отметим некоторые свойства векторов линейного пространства.
1. Если среди векторов 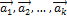 имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если например,
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если например, 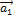 =
= 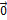 , то равенство (4.2.1) справедливо при
, то равенство (4.2.1) справедливо при 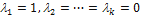 .
.
2. Если часть векторов 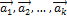 являются линейно зависимыми, то и все эти векторы – линейно зависимые. Действительно, если, например, векторы
являются линейно зависимыми, то и все эти векторы – линейно зависимые. Действительно, если, например, векторы 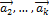 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 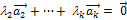 , в котором не все числа равны нулю. Но тогда с теми же числами
, в котором не все числа равны нулю. Но тогда с теми же числами 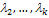 и
и 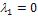 будет справедливо равенство (4.2.1).
будет справедливо равенство (4.2.1).
Пример 1. Выяснить, являются ли векторы 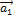 = (1, 3, 1, 3),
= (1, 3, 1, 3), 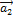 = (2, 1, 1, 2) и
= (2, 1, 1, 2) и 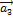 = (3, -1, 1, 1) линейно зависимыми.
= (3, -1, 1, 1) линейно зависимыми.
Решение. Составим векторное равенство  . Записывая
. Записывая 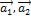 ,
, 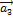 в виде вектор-столбцов, получим
в виде вектор-столбцов, получим
 +
+ 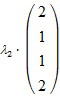 +
+ 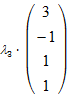 =
=  .
.
Задача свелась к решению системы:
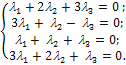
Решая систему методом Гаусса, приведём её к виду:

откуда найдём бесконечное множество её решений: (t, 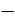 2t, t), где t– произвольное действительное число.
2t, t), где t– произвольное действительное число.
Для данных векторов условие (4.2.1) выполняется не только при 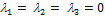 ,например, также при
,например, также при 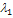 = 1;
= 1; 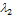 =
= 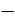 2;
2; 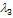 = 1. Следовательно, эти векторы – линейно зависимые.
= 1. Следовательно, эти векторы – линейно зависимые.
Определение. Линейное пространство 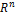 называется n-мерным, если в нём существует nлинейно независимых векторов, а любые из (n + 1) векторов уже являются зависимыми.
называется n-мерным, если в нём существует nлинейно независимых векторов, а любые из (n + 1) векторов уже являются зависимыми.
Определение. Размерностью линейного пространства называют максимальное число содержащихся в нём линейно независимых векторов. Число nназывается размерностью пространства  и обозначается
и обозначается  .
.
Определение. Совокупность nлинейно независимых векторов n-мерного пространства  называется базисом.
называется базисом.
Теорема (о базисе линейного пространства). Каждый вектор  линейного пространства
линейного пространства  можно представить и притом единственным образом в виде линейной комбинации векторов базиса.
можно представить и притом единственным образом в виде линейной комбинации векторов базиса.
Доказательство. Пусть векторы 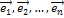 образуют произвольный базис n-мерного пространства
образуют произвольный базис n-мерного пространства  . Так как любые из (n + 1) векторов n-мерного пространства
. Так как любые из (n + 1) векторов n-мерного пространства  зависимы, то будут зависимы, в частности, векторы
зависимы, то будут зависимы, в частности, векторы 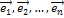 и рассматриваемый вектор
и рассматриваемый вектор  . Тогда существуют такие не равные одновременно нулю числа
. Тогда существуют такие не равные одновременно нулю числа 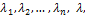 что
что
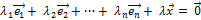 .
.
При этом 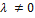 , ибо в противном случае, если
, ибо в противном случае, если 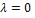 и хотя бы одно из чисел
и хотя бы одно из чисел 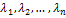 было бы отлично от нуля, то векторы
было бы отлично от нуля, то векторы 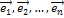 были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,
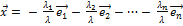 или
или
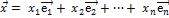 , (4.2.2),
, (4.2.2),
где 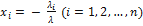 .
.
Это выражение 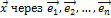 единственное, так как если допустить какое-либо другое выражение, например,
единственное, так как если допустить какое-либо другое выражение, например,
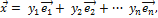
то, вычитая из него почленно (4.2.2), получим
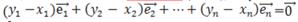 ,
,
откуда из условия линейной независимости векторов 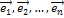 следует, что
следует, что
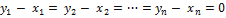
или
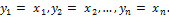
Равенство (4.2.2) называется разложением вектора  по базису
по базису 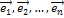 , а числа
, а числа 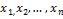 – координатами вектора
– координатами вектора  относительно этого базиса. В силу единственности разложения (4.2.2) каждый вектор однозначно может быть определён координатами в некотором базисе.
относительно этого базиса. В силу единственности разложения (4.2.2) каждый вектор однозначно может быть определён координатами в некотором базисе.
Справедлива следующая теорема.
Теорема. Если 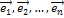 – система линейно независимых векторов линейного пространства и любой вектор
– система линейно независимых векторов линейного пространства и любой вектор  линейно выражается через
линейно выражается через 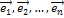 , то пространство является n-мерным, а векторы
, то пространство является n-мерным, а векторы 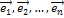 – его базисом.
– его базисом.
Пример 2. Даны векторы 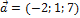 ,
,  в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 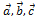 образуют базис, и найти координаты
образуют базис, и найти координаты 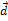 в этом базисе.
в этом базисе.
Решение. Векторы 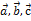 образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор
образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор 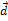 нельзя разложить по данному базису.
нельзя разложить по данному базису.
D = 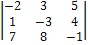 = 290.
= 290.
Так как D = 290 ≠ 0, то векторы 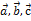 линейно независимы и образуют базис. Следовательно, вектор
линейно независимы и образуют базис. Следовательно, вектор 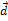 можно единственным образом разложить по данному базису:
можно единственным образом разложить по данному базису: 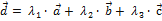 . Здесь
. Здесь 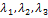 - координаты вектора
- координаты вектора 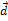 в базисе (
в базисе ( 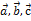 ). В координатной форме получим систему:
). В координатной форме получим систему:
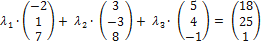 или
или 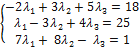 .
.
Найдём координаты вектора 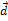 в этом базисе.
в этом базисе.
а) решение по формулам Крамера:
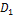 =
= 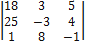 = 580;
= 580;  =
= 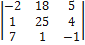 = -290;
= -290; 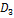 =
= 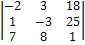 = 1450
= 1450
По формулам Крамера находим координаты вектора 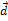 :
:
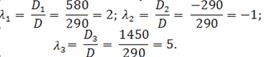 ,
,
следовательно, 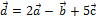 или
или 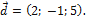
б) решение методом Гаусса:
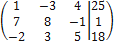 ~
~ 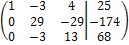 ~
~  ~
~ 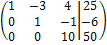
Последней матрице соответствует следующая система:
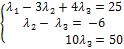
Решая эту систему, находим 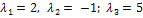 , т.е.
, т.е. 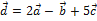 .
.
Раздел 4.3. Преобразование координат при переходе к новому базису
Пусть в пространстве  имеются два базиса: старый
имеются два базиса: старый 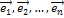 и новый
и новый 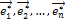 . Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
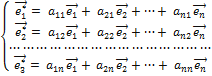 (4.3.1)
(4.3.1)
Сознательно применили необычную индексацию: здесь в матрице коэффициентов второй индекс обозначает номер строки и первый – номер столбца.
Матрица
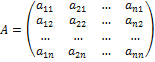
называется матрицей перехода от старого базиса 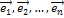 к новому
к новому 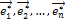 .
.
Коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица А – невырожденная, так как в противном случае её столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 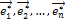 к старому базису
к старому базису 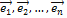 осуществляется с помощью обратной матрицы А-1.
осуществляется с помощью обратной матрицы А-1.
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор  имеет координаты (
имеет координаты ( 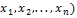 относительно старого базиса и координаты (
относительно старого базиса и координаты ( 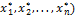 относительно нового базиса, т.е.
относительно нового базиса, т.е.
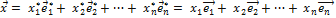 (4.3.2).
(4.3.2).
Подставив значения 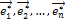 из системы (4.3.1) в левую часть (4.3.2), получим после преобразований:
из системы (4.3.1) в левую часть (4.3.2), получим после преобразований:

а в матричной форме
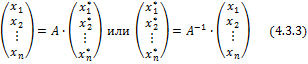 .
.
Пример 3. Дан вектор  . Разложить этот вектор по новому базису, связанному со старыми базисом уравнениями
. Разложить этот вектор по новому базису, связанному со старыми базисом уравнениями
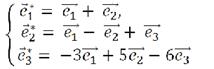
Решение. Матрица перехода от старого базиса 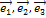 к новому базису
к новому базису 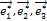 имеет вид
имеет вид
А = 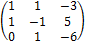 =>
=> 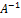 =
= 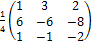 (проверить самостоятельно!)
(проверить самостоятельно!)
По формулам (4.3.3) находим:
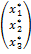 =
=  =
= 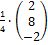 =
= 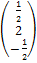 .
.
Следовательно, вектор  в новом базисе может быть представлен в виде:
в новом базисе может быть представлен в виде:
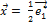 + 2
+ 2 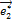 -
- 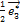 .
.
Дата: 2019-12-10, просмотров: 374.