Рассмотрим два линейных пространства:  размерности n
размерности n 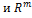 размерности m .
размерности m .
Определение. Если задан закон по которому каждому вектору 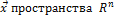 ставится в соответствие единственный вектор
ставится в соответствие единственный вектор 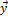 из
из 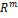 ,
,
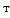 о говорят, что задан оператор(преобразование) Ã(
о говорят, что задан оператор(преобразование) Ã( 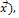 действующий из
действующий из 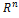 в
в 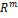 , и записывают
, и записывают 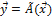 .
.
Оператор (преобразование) называется линейным, если для любых векторов 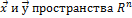 и любого числа
и любого числа 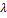 выполняются соотношения:
выполняются соотношения:
1. Ã( 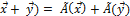 –свойство аддитивности оператора;
–свойство аддитивности оператора;
2. Ã( 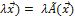 – свойство однородности оператора.
– свойство однородности оператора.
Вектор  =Ã(
=Ã(  называется образом вектора
называется образом вектора  , а если сам вектор
, а если сам вектор  – прообразом вектора
– прообразом вектора  Если пространства
Если пространства  и
и  совпадают, то оператор Ã отображает пространство
совпадают, то оператор Ã отображает пространство  в себя. В этом параграфе мы будем рассматривать именно такие операторы.
в себя. В этом параграфе мы будем рассматривать именно такие операторы.
Выберем в пространстве  базис
базис 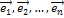 и запишем разложение вектора
и запишем разложение вектора  по данному базису:
по данному базису:
 .
.
В силу линейности оператора Ã получаем
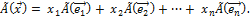
Поскольку Ã( 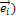 (i = 1, 2…, n) – также вектор из
(i = 1, 2…, n) – также вектор из 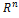 , то его можно разложить по базису
, то его можно разложить по базису 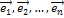 . Пусть
. Пусть
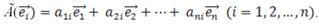 (4.5.1).
(4.5.1).
Тогда
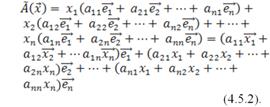 .
.
С другой стороны, вектор 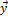 = Ã(
= Ã( 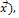 имеющий в том же базисе
имеющий в том же базисе 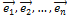 координаты
координаты 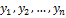 , можно записать так:
, можно записать так:
à 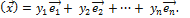 (4.5.3).
(4.5.3).
Ввиду единственности разложения вектора по базису равны правые части равенства (4.5.2) и (4.5.3), откуда
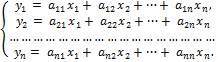
Матрица А = ( 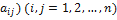 называется матрицей оператора Ã в базисе
называется матрицей оператора Ã в базисе 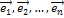 , а ранг r матрицы А – рангом оператора Ã.
, а ранг r матрицы А – рангом оператора Ã.
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. И обратно: всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.
Связь между вектором 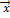 и его образом
и его образом 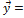 Ã(
Ã( 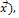 можно выразить в матричной форме уравнением
можно выразить в матричной форме уравнением
У = АХ, (4.5.4),
гдеА – матрица линейного оператора,
Х = 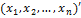 , У =
, У = 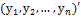 ; матрицы – столбцы из координат векторов
; матрицы – столбцы из координат векторов  и
и 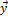 .
.
Пример 6. Линейный оператор Ã в базисе 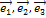 задан матрицей
задан матрицей
А = 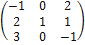 . Найти
. Найти 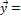 Ã
à 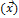 , где
, где  =
= 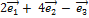 .
.
Решение. По формуле (4.5.4) имеем
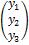 =
= 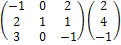 =
= 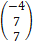 .
.
Следовательно, 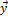 =
= 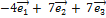 .
.
Определим действия над линейными операторами.
Суммой двух линейных операторов 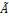 и
и  называется оператор (
называется оператор ( 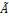 +
+ 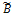 ), определяемый равенством :(
), определяемый равенством :( 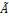 +
+  )(
)( 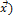 =
= 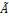 (
( 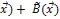 .
.
Произведением линейного оператора Ã на число 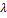 называется оператор
называется оператор 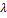 Ã, определяемый равенством:
Ã, определяемый равенством: 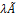 (
( 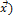 =
= 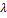 (
( 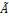 (
( 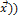 .
.
Произведением линейных операторов 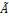 и
и  называется оператор
называется оператор  , определяемый равенством:
, определяемый равенством:  (
( 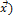 =
= 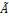 (
(  (
( 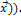
Можно убедиться в том, что операторы ( 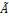 +
+  ),
), 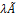 ,
,  , полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
, полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
Линейный оператор называется нулевым Õ, если он переводит все векторы пространства  в нулевые векторы: Õ(
в нулевые векторы: Õ( 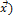 =
= 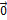 .
.
Линейный оператор называется тождественным Ẽ, если он преобразует любой вектор  в самого себя, т.е. Ẽ(
в самого себя, т.е. Ẽ( 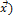 =
=  .
.
Теорема. Матрицы А и 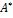 линейного оператора Ã в базисах
линейного оператора Ã в базисах
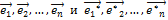 связаны соотношением
связаны соотношением
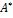 =
= 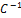 АС, (4.5.5),
АС, (4.5.5),
где С – матрица перехода от старого базиса к новому.
Доказательство. Аналогом формулы (4.5.4) в новом базисе 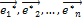 является равенство
является равенство
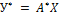 (4.5.6)
(4.5.6)
Так как С – матрица перехода от старого базиса к новому, то в соответствии с формулой (4.3.3)
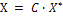 (4.5.7),
(4.5.7),
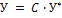 (4.5.8).
(4.5.8).
Умножив равенство (4.5.7) слева на матрицу А, получим АХ = АС 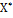 или с учётом (4.5.4) У = АС
или с учётом (4.5.4) У = АС  . Следовательно, учитывая (4.5.8) получим С
. Следовательно, учитывая (4.5.8) получим С 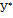 = АС
= АС 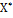 или
или 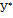 =
= 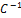 АС
АС  . Сравнивая последнее выражение с (4.5.6), получим доказываемую формулу (4.5.5).
. Сравнивая последнее выражение с (4.5.6), получим доказываемую формулу (4.5.5).
Пример 7. Линейный оператор Ã в базисе 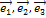 имеет матрицу
имеет матрицу
А = 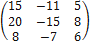 .
.
Найти его матрицу в базисе
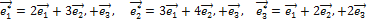 .
.
Решение. Матрица перехода С = 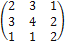 . Матрица
. Матрица 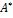 оператора Ã в новом базисе:
оператора Ã в новом базисе: 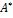 =
=  А
А 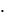 С. Так как
С. Так как
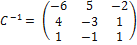 ,
,
то по формуле (4.5.5):
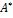 =
=  А
А  С=
С=  .
.
Дата: 2019-12-10, просмотров: 354.