Определение. Квадратичной формой называется однородный многочлен L( 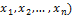 второй степени от
второй степени от 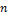 переменных.
переменных.
Примерами квадратичных форм являются
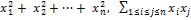 ,
,

Согласно данному определению коэффициентами квадратичной формы могут быть любые числа (в том числе и комплексные). Если все коэффициенты квадратичной формы вещественны, то она называется вещественной. Если же в качестве коэффициентов квадратичной формы допускаются комплексные числа, то она называется комплексной квадратичной формой.
Укажем для квадратичных форм одну специальную форму записи. Считая, что в формеL( 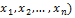 уже выполнено приведение подобных членов, обозначим коэффициент при
уже выполнено приведение подобных членов, обозначим коэффициент при 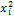 через
через  , а коэффициент при
, а коэффициент при 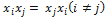 через
через
2 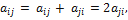
так что
 (5.1.1)
(5.1.1)
Для члена, содержащего 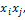 мы получим тогда следующую симметричную форму записи:
мы получим тогда следующую симметричную форму записи:
2 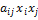 =
= 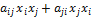 .
.
Вся квадратичная форма может быть записана теперь в виде L( 
= 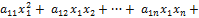
+ 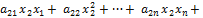
… … … … … … … … … … … … … … …
+ 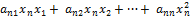 . (5.1.2).
. (5.1.2).
Определение. Квадратичной формой от вещественных переменных  называют функцию L(
называют функцию L( 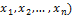 , заданную равенством
, заданную равенством
L( 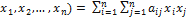 ,
, 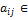 R (5.1.3)
R (5.1.3)
Ясно, что коэффициенты 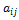 квадратичной формы L в записи (5.1.2) определены однозначно. Составленная из них матрица
квадратичной формы L в записи (5.1.2) определены однозначно. Составленная из них матрица
А = 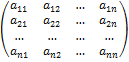
называется матрицей квадратичной формы.
Ввиду условия (5.1.1) элементы матрицы А, расположенные симметрично относительно главной диагонали, равны между собой. Следовательно, А  =А (или
=А (или 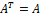 ), т.е. А –симметричная матрица.
), т.е. А –симметричная матрица.
Очевидно, что для любой симметричной матрицы А всегда можно указать такую квадратичную форму, что её матрица совпадает с А. Если две квадратичные формы имеют одну и ту же матрицу, то эти формы могут отличаться друг от друга только обозначением переменных, что не имеет существенного значения. Две такие квадратичные формы можно считать одинаковыми. Таким образом, квадратичные формы определяются своими матрицами.
В матричной записи квадратичная форма имеет вид:
L = X 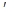 AX, (5.1.4),
AX, (5.1.4),
где X = 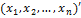 — матрица-столбец (вектор-столбец) переменных.
— матрица-столбец (вектор-столбец) переменных.
В самом деле:
L =( 
=( 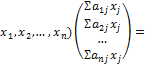
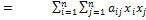 , что доказывает равносильность формул (5.1.3) и (5.1.4).
, что доказывает равносильность формул (5.1.3) и (5.1.4).
Пример 1. Дана квадратичная форма L( 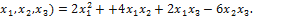 Записать ее в матричном виде.
Записать ее в матричном виде.
L( 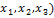 , = 2
, = 2 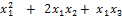 +
+
+ 2 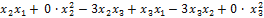 .
.
Следовательно,
L( 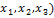 = (
= ( 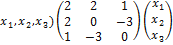 .
.
Ранг матрицы А называют рангом квадратичной формы. В случае, когда ранг матрицы равен числу переменных, форма называется невырожденной.
Пусть теперь нам задано линейное преобразование переменных
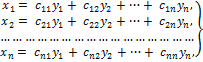 (5.1.5),
(5.1.5),
выражающее переменные  через систему переменных
через систему переменных 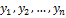 . Если через С мы обозначим матрицу преобразования (5.1.5), а через Х и У – столбцы из старых и новых переменных соответственно, то преобразование (5.1.5) примет следующую матричную форму:
. Если через С мы обозначим матрицу преобразования (5.1.5), а через Х и У – столбцы из старых и новых переменных соответственно, то преобразование (5.1.5) примет следующую матричную форму:
Х = СУ. (5.1.6).
Будем рассматривать исключительно невырожденные линейные преобразования переменных, т.е. будем предполагать, что detС = ⃒С⃒ ≠ 0. В этом случае для преобразования (5.1.6) существует обратное преобразование
У = 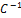 Х, (5.1.7),
Х, (5.1.7),
выражающее новые переменные через старые.
Подставив выражение для  из преобразования (5.1.5) в квадратичную форму L(
из преобразования (5.1.5) в квадратичную форму L( 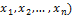 , получим
, получим
L( 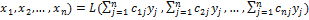 .
.
После выполнения всех необходимых действия правая часть превратится в квадратичную форму 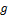 (
( 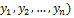 от новых переменных
от новых переменных 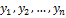 . В этом случае, будем говорить, что форма
. В этом случае, будем говорить, что форма 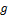 (
( 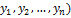 получена из L(
получена из L( 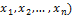 в результате линейного преобразования переменных (5.1.5).
в результате линейного преобразования переменных (5.1.5).
Очевидно, если полученную форму 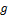 (
( 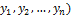 подвергнуть обратному линейному преобразованию переменных (5.1.7), то мы вернёмся к исходной квадратичной форме L(
подвергнуть обратному линейному преобразованию переменных (5.1.7), то мы вернёмся к исходной квадратичной форме L( 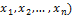 .
.
Пример 2. Подвергнем форму L( 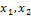 ) =
) = 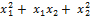 преобразованию
преобразованию
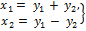 .
.
Решение. Получим форму
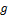 =
= 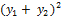 +(
+( 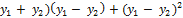 = 3
= 3 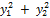 .
.
Подвергая её обратному преобразованию
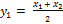 ,
, 
приходим к исходной форме
3 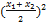 +
+ 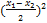 =
= 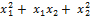 .
.
Выясним, как меняется матрица квадратичной формы при линейном преобразовании переменных.
Подвергнем форму (5.1.4) преобразованию (5.1.6). Так как X=(СУ)  = =У
= =У 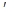 С
С 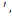 то мы получим
то мы получим
L = X 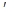 AX = У
AX = У 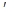 С
С 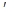 АСУ = У
АСУ = У 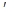 ( C
( C 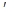 AC )У =
AC )У = 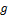 (
( 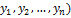 .
.
Рассмотрим квадратную матрицу 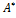 = С
= С 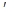 АС. Так как
АС. Так как
( 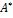 )
)  = (C
= (C 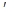 AC)
AC)  =C
=C 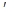 A
A  C
C 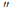 = C
= C 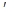 AC =
AC = 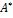 ,
,
то матрица 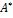 симметрична, а значит она и является матрицей квадратичной формы
симметрична, а значит она и является матрицей квадратичной формы 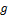 = У
= У 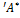 У. Таким образом, можно сформулировать следующую теорему.
У. Таким образом, можно сформулировать следующую теорему.
Теорема. Если в квадратичной форме с матрицей А сделано линейное преобразование переменных с матрицей С, то полученная квадратичная форма будет иметь матрицу С 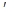 AC.
AC.
Пример 3. Дана квадратичная форма L(  = 2
= 2 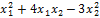 . Найти квадра-тичную форму
. Найти квадра-тичную форму 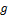 (
( 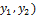 , полученную из данной линейным преобразованием.
, полученную из данной линейным преобразованием.
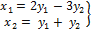 .
.
Решение. Матрица данной квадратичной формы А =  , а матрица линейного преобразования С =
, а матрица линейного преобразования С = 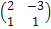 . Следовательно, по теореме матрицей искомой квадратичной формы
. Следовательно, по теореме матрицей искомой квадратичной формы
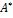 =
= 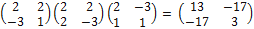 .
.
Таким образом, квадратичная форма имеет вид 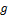 (
( 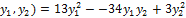 .
.
Дата: 2019-12-10, просмотров: 363.