Определение. Вектор 
≠ 
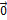называется собственным вектором линейного оператора Ã, если найдётся такое число 
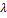, что
Ã(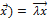 
(4.6.1).
Само число 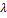называется собственным значением или характеристическим числом линейного оператора (преобразования) Ã, соответствующим вектору .
Равенство (4.6.1) можно записать в матричной форме:
А = 
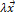или (А – 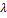Е) = 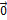(4.6.2).
В развёрнутом виде получим:
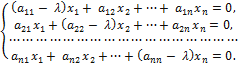
Полученная однородная система всегда имеет нулевое решение = = 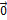=(0, 0, …, 0). Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы
⃒А- 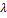Е⃒= 
.
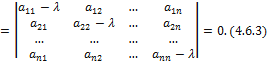Определитель⃒А- 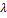Е⃒является многочленом n-ой степени относительно 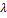. Этот многочлен называется характеристическим многочленом оператора Ã или матрицы А.
Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, пусть ⃒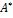 
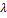- Е⃒— характеристический многочлен, полученный в новом базисе 
, а С– матрица перехода от старого базиса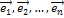 
к новому. С учётом (4.5.5) получим
= 
= 
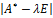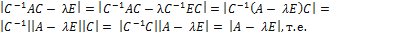
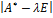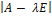независимо от выбора базиса.
Пример 8. Найти собственные значения и собственные векторы линейного оператора Ã заданного матрицей.
А = 
.
Решение. Составляем характеристическое уравнение
⃒ 
= 
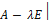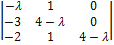= 0 или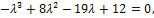 
откуда и находим собственные значения линейного оператора Ã:
.
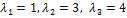Находим собственный вектор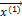 
= ( 
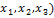, соответствующий собственному значению 
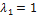. Для этого решаем матричное уравнение
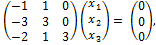
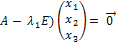или 
( 
или 
для чего и находим общее решение и фундаментальную систему решений однородной системы линейных уравнения (ОСЛУ):
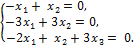
Приведём матрицу системы к ступенчатому виду:
.
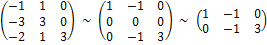Так как r(A) =r(Ã) = 2 < 3 = n, то система неопределенна. В качестве главных переменных можно выбрать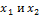 
, а в качестве свободной переменной - 
.
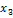Запишем систему, соответствующую полученной матрице:
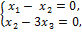
откуда получим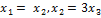 
. Обозначив 
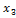через с, получим, что векторы 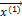= (3с, 3с, c) = c(3, 3, 1) при любом с ≠ 0 являются собственными векторами линейного оператора Ã с собственным значением 
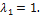Фундаментальная система решений состоит из одного вектора (3, 3, 1), который является собственным вектором, соответствующим собственному значению :
.
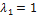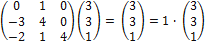Аналогично можно убедиться в том, что векторы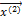 
= ( 
= 
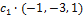при любом 
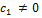являются собственными векторами линейного оператора Ã с собственным значением 
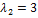, а векторы 
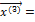(0, 0, 
) = 
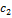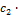(0, 0, 1) при любом 
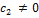являются собственными векторами линейного оператора Ã с собственным значением 
.
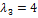Наиболее простой вид принимает матрица А линейного оператора Ã, имеющего n линейно независимых собственных векторов 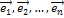с собственными значениями, соответственно равными 
.
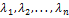Теорема 1. Матрица А линейного оператора Ã в некотором базисе диагональна тогда и только тогда, когда все базисные векторы являются собственными векторами линейного оператора Ã, при этом диагональные элементы матрицы линейного оператора являются собственными значениями линейного оператора.
Доказательство. Пусть базисные векторы 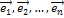являются собственными векторами линейного оператора Ã. Тогда Ã( 
= 
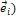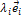(i= 1, 2, …, n) или с учётом (4.5.1)
Ã(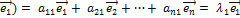 
,
Ã(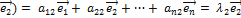 
,
…………………………….………………………………………
Ã(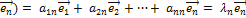 
,
откуда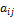 
= 0, если i≠ j, и 
= 
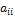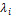, если i= j. Таким образом, матрица линейного оператора Ã в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
= 
.
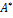Верно и обратное: если матрица А линейного оператора Ã в некотором базисе является диагональной, то все векторы этого базиса – собственные векторы оператора Ã.
Теорема 2. Собственные векторы линейного оператора, отвечающие его различным значениям, линейно независимы.
Доказательство. Докажем утверждение по индукции. Пусть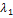 
≠ 
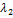– собственные значения оператора Ã, а 
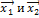– соответствующие имсобственные векторы. Предположим, что они линейно зависимы, тогда существует 
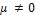такое, что
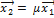. (4.6.4).
Подействуем на обе части последнего равенства оператором Ã.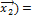
Ã( 
à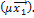 
Учитывая линейность Ã и то, что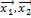 
– собственные векторы, получим
(4.6.5).
Подставим в (4.6.5) выражение для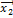 
из (4.6.4)
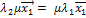или 
) 
.
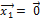Учитывая, что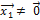 
( 
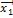– собственный вектор) и 
получаем
,
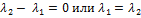что противоречит тому, что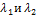 
– различные собственные значения.
Допустим, что любой набор собственных векторов 
, отвечающих различным собственным значениям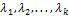 
оператора Ã, линейно независим. Докажем, что тогда и любой набор 
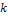+1 собственных векторов, отвечающих различным собственным значениям, линейно независим.
Предположим, что это неверно, т.е. существует ненулевой набор чисел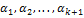 
таких, что
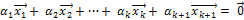(4.6.6).
Очевидно, что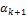 
≠ 0, иначе (4.6.6) означало бы линейную зависимость векторов . Преобразуем (4.6.6):
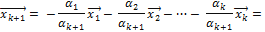
(4.6.7).
Ясно, что
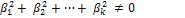(4.6.8).
Подействуем на обе части (4.6.7) оператором Ã.
Учитывая линейность Ã и то, что 
, - собственные векторы оператора Ã, получаем
(4.6.9).
Подставим в левую часть (4.6.9) выражения для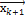 
из (4.6.7)
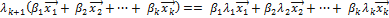
или
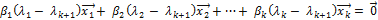. (4.6.10)
Учитывая, что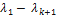 
≠ 0,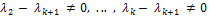 
и (4.6.8), получаем из (4.6.10), что векторы линейно зависимы, а это противоречит индуктивному предположению.
Из этих теорем ещё не следует, что для любого линейного оператора должен существовать базис, в котором матрица оператора диагональна, т.е. базис пространства, составленный из собственных векторов линейного оператора. Приведём контрпример.
Пример 9. Линейный оператор Ã в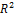 
в базисе 
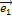= (1, 0), 
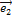= (0, 1)имеет матрицу
А =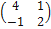 
.
Доказать, что для оператора Ã не существует базиса, в котором его матрица диагональна.
Решение. Найдём собственные значения оператора Ã.
⃒ 
= 
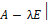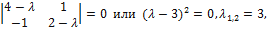
т.е. оператор Ã имеет только одно собственное значение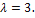 
Найдём собственные векторы, отвечающие этому собственному значению. Для этого решаем матричное уравнение
= 
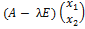или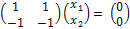 
.
Найдём фундаментальную систему решений ОСЛУ:
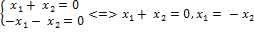
Обозначив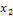 
черезс, получим, что векторы 
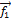= (-c, с) = c 
(-1, 1) при любом с ≠ 0 являются собственными векторами линейного оператора Ã с собственным значением 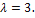Фундаментальная система решений состоит из одного вектора (-1, 1), который является собственным вектором. Значит, имеется только один линейно независимый собственный вектор (-1, 1), а из него не построить базис пространства 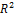(т.к. dim 
.
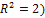Следствие (из теоремы 1). Если линейный оператор Ã в n-мерном вещественном пространстве имеет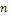 
различных вещественных собственных значений 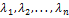, то каждому собственному значению соответствует только один линейно независимый собственный вектор и эти векторы образуют базис пространства и матрица оператора А в этом базисе имеет вид
.
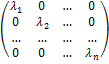Пример 10. Привести матрицу А линейного оператора Ã к диагональному виду.
А = .
Решение. В примере 8 были найдены собственные значения матрицы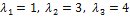 
и соответствующие им собственные векторы 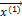= (3, 3, 1), 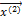= (-1, -3, 1) и 
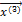= (0, 0, 1). Так как координаты этих векторов не пропорциональны, то они линейно независимы. Поэтому в базисе, состоящем их этих собственных векторов 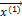, , 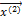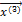матрица А будет иметь диагональный вид:
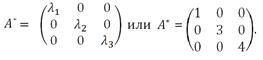
Это легко проверить, взяв, например, в качестве базиса линейно независимые собственные векторы 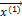=(3, 3, 1), 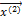= (-1, -3, 1) и 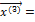(0, 0, 1). Матрица С перехода от старого базиса к новому в этом случае имеет вид:
С =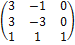 
.
Тогда в соответствии с (4.5.5) матрица 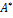в новом базисе 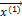, , 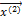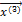примет вид:
= 
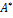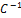АС=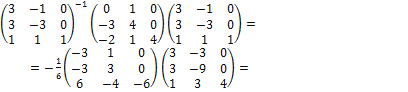 
.
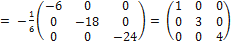Контрольные вопросы к главе 4
1. Что называется n-мерным вектором?
2. Какими свойствами обладают операции над n-мерными векторами?
3. Приведите примеры линейных пространств.
4. Что называется линейной комбинацией векторов?
5. Что такое размерность линейного пространства?
6. Что называется базисом векторов n-мерного пространства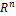 
?
Тесты к главе 4
- Для того чтобы число λ было собственным вектором собственным подпространством векторным пространством собственным значением линейного
оператора А, необходимо и достаточно, чтобы оно являлось степенью корнем значением элементом характеристического многочлена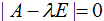 
,
где А – матрица оператора, а Е – обратная матрица матрица единичная матрица нулевая матрица той же размерности.
- Множество всех собственных значений называется
| рангом |
| спектром |
| следом |
| порядком |
| характером |
| определителем |
- Если
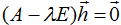, то для линейного оператора с матрицей А
вектор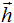 
является
| направляющим |
| присоединенным |
| собственным |
| ортогональным |
| базисным |
| проекцией |
- Если
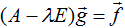, где – присоединенный вектор i-го порядка к собственному вектору 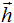, то вектор 
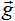является
| нулевым вектором |
| собственным вектором |
| присоединенным вектором (i–1)-го порядка к собственному вектору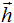
|
| тоже присоединенным вектором i-го порядка к собственному вектору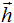
|
| присоединенным вектором (i+1)-го порядка к собственному вектору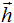
|
| вектором, коллинеарным вектору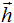
|
4. Собственные векторы линейного оператора, соответствующие различным собственным значениям, непременно являются
| равными |
| попарно различными |
| базисом в пространстве, где действует оператор |
| попарно ортогональными |
| линейно зависимыми |
| линейно независимыми |
- Найти значение а, при котором
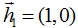и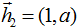 
являются базисом
из собственных векторов линейного оператора, заданного матрицей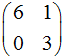 
Ответ введите, заполнив форму:
+ –
- Найти собственные значения линейного оператора, заданного
матрицей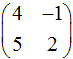 
. В качестве ответа выбрать их сумму.
Введите ответ: 0 1 2 3 4 5 6 7 8 9 10
- Одно из собственных значений линейного оператора, заданного
матрицей,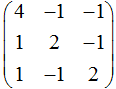 
равно 2.
В ответе выбрать другое собственное значение.
Введите ответ:
0 1 2 3 4 5 6 7 8 9 10
Глава 5. Квадратичные формы
Дата: 2019-12-10, просмотров: 266.
