Раздел 4.1. n – мерный вектор и векторное пространство
Определение. Упорядоченная совокупность n чисел (  ) называется n-мерным вектором. Числа
) называется n-мерным вектором. Числа  называются компонентами (координатами) вектора.
называются компонентами (координатами) вектора.
Векторы 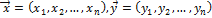 равны, если они совпадают покоординатно:
равны, если они совпадают покоординатно:
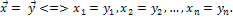
Операция сложения и умножения n-мерных векторов вводятся по аналогии с обычными векторами, т.е. покоординатно. Свойства обычных векторов, которые мы доказывали, становятся, таким образом, определениями для n-мерных векторов. Итак, пусть 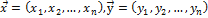 ∈
∈  ,
,
l - число. Тогда по определению

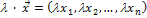
Операции над n-мерными векторами обладают теми же алгебраическими свойствами, что и операции над векторами на плоскости и в пространстве:
1. Сложение векторов коммутативно: 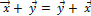 .
.
2. Сложение векторов ассоциативно:  .
.
3. Существует нулевой вектор 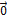 = (0, 0, …, 0) такой, что
= (0, 0, …, 0) такой, что 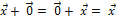 .
.
4. Для любого вектора 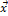 существует противоположный вектор (-
существует противоположный вектор (- 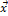 ) такой, что
) такой, что 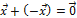 .
.
5. Умножение на число ассоциативно: l( 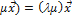 .
.
6. Умножение на число дистрибутивно относительно сложения чисел: (l 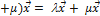 .
.
7. Умножение на число дистрибутивно относительно сложения векторов: l(  .
.
8. 1 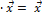 для любого вектора
для любого вектора 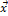 .
.
Все эти свойства следуют непосредственно из определений операций. Существование противоположного вектора -  позволяет внести вычитание векторов:
позволяет внести вычитание векторов:  =
= 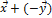 = (
= ( 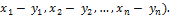
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведённым выше свойствам, называется линейным (или векторным) пространством.
Примеры линейных пространств.
1. Пространство 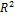 – геометрических векторов на плоскости.
– геометрических векторов на плоскости.
2. Пространство 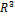 – геометрических векторов в трёхмерном пространстве.
– геометрических векторов в трёхмерном пространстве.
3. Множество матриц 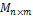 (R) относительно операций сложения матриц и умножения матрицы на число образует линейное пространство.
(R) относительно операций сложения матриц и умножения матрицы на число образует линейное пространство.
4. 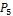 (R) – множество многочленов с вещественными коэффициентами степени не выше 5-й образует линейное пространство относительно операций сложения многочленов и умножения многочлена на вещественное число.
(R) – множество многочленов с вещественными коэффициентами степени не выше 5-й образует линейное пространство относительно операций сложения многочленов и умножения многочлена на вещественное число.
Из приведённых примеров видно, что элементы линейных пространств могут быть совершенно различной природы (векторы, матрицы, многочлены).
Отметим простейшие свойства линейных пространств, следующие из определения.
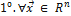 , 0
, 0 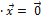 ;
;
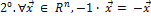 ;
;
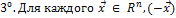 определен однозначно.
определен однозначно.
Доказательство 
 , т.е.
, т.е. 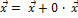
Прибавим к обеим частям -  :
:
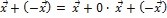 , тогда
, тогда
 , т.е. 0
, т.е. 0 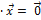
Доказательство  :
:
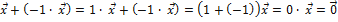 .
.
Тогда мы имеем
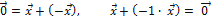 =>
=> 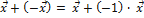 .
.
Прибавим к обеим частям -  :
:
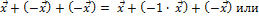

 => -
=> - 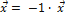 .
.
Доказательство 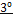 : Допустим противное, т.е. что существует такой элемент
: Допустим противное, т.е. что существует такой элемент  , у которого два противоположных элемента -
, у которого два противоположных элемента -  и -
и -  , т.е.
, т.е.
- 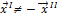 и
и  ,
, 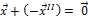 ,
,
тогда
- 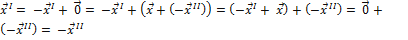 .
.
Получили, что - 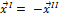 , что противоречит нашему допущению.
, что противоречит нашему допущению.
Замечание. В определении линейного пространства поле вещественных чисел можно заменить на произвольное числовое поле Р (например С-поле комплексных чисел или Z-поле целых чисел). В этом случае говорят о линейном пространстве над полем Р. Если поле Р =R, линейное пространство называют вещественным.
Определение. Линейным подпространством векторного пространства  называется непустое множество L
называется непустое множество L 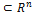 , обладающее следующими свойствами:
, обладающее следующими свойствами:
1) 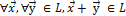 ;
;
2)  .
.
Примеры:
- 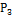 (R) является подпространством пространства
(R) является подпространством пространства 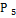 (R).
(R).
- Множество матриц вида
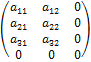 ,
, 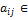 R
R
является линейным подпространством пространства 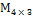 (R).
(R).
Очевидно, ноль–пространство - 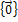 и
и  всегда являются подпространствами
всегда являются подпространствами  , они называются его несобственными подпространствами. Если у пространства есть и другие подпространства, то они называются собственными.
, они называются его несобственными подпространствами. Если у пространства есть и другие подпространства, то они называются собственными.
Определение. Суммой двух линейных подпространств 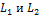 векторного пространства
векторного пространства 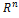 называется совокупность S=
называется совокупность S= 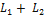 всех векторов из
всех векторов из  , каждый из которых представляется в виде
, каждый из которых представляется в виде 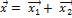 , где
, где 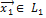 и
и 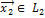 .
.
Определение. Пересечением двух линейных подпространств 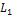 и
и 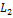 векторного пространства
векторного пространства  называется совокупность D=
называется совокупность D= 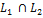 всех векторов из
всех векторов из  , каждый из которых принадлежит как
, каждый из которых принадлежит как 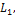 так и
так и 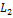 .
.
Определение. Прямой суммой двух линейных подпространств 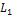 и
и 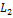 векторного пространства
векторного пространства  называется сумма этих подпространств при условии, что их пересечение состоит лишь из нулевого вектора, т.е.
называется сумма этих подпространств при условии, что их пересечение состоит лишь из нулевого вектора, т.е. 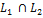 =
= 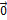 .
.
В случае прямой суммы будем писать
S = 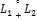 или S=
или S= 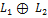 .
.
Дата: 2019-12-10, просмотров: 384.