Раздел 3.1. Векторы. Основные понятия
Вектор – это направленный отрезок. Если А – начало вектора, а В – его конец, то вектор обозначается 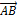 или
или  . Вектор
. Вектор 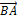 называется противоположным вектору
называется противоположным вектору 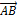 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , обозначается -
, обозначается -  .
.
Длиной или модулем вектора 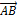 называется длина отрезка и обозначается |
называется длина отрезка и обозначается | 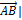 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 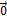 . Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором и обозначается через
. Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором и обозначается через 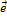 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается 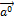 .
.
Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записываются
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записываются  ||
||  .
.
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора  и
и  называются равными (
называются равными (  =
=  ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трёх векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Для суммы двух векторов есть правило треугольника, а также правило параллелограмма.
Произведением вектора  на число
на число 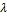 называется вектор
называется вектор 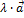 или (
или ( 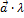 ),который имеет длину |
),который имеет длину | 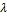 |
| 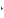 |
|  |, коллинеарен вектору
|, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если
, если 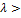 0 и противоположное направление, если
0 и противоположное направление, если 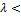 0.
0.
Из определения произведения вектора на число следуют свойства этого произведения:
1) если  =
= 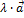 , то
, то  ||
||  . Наоборот, если
. Наоборот, если  ||
||  , (
, (  ≠
≠ 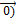 ,то при некотором
,то при некотором 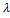 верно равенство
верно равенство  =
= 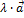 ;
;
2)  = |
= |  |
|  , т.е. каждый вектор равен произведению его модуля на орт.
, т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1. 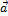 +
+ 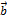 =
= 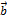 +
+ 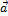 ,
,
2. ( 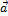 +
+ 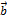 ) +
) + 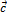 =
= 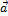 +(
+( 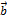 +
+ 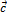 ),
),
3. 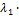 (
( 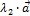 ) =
) = 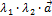
4. 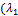 +
+ 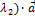 =
= 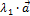 +
+ 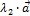 ,
,
5. 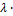 (
( 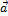 +
+ 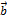 ) =
) =  +
+  .
.
Пусть в пространстве задана ось 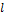 . Проекцией точки М на ось
. Проекцией точки М на ось 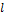 называется основание
называется основание 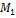 перпендикуляра
перпендикуляра 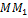 , опушенного из точки на ось (см. рис. 1)
, опушенного из точки на ось (см. рис. 1)

Проекцией вектора 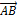 на ось
на ось 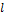 называется положительное число
называется положительное число 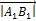 , если вектор
, если вектор 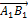 и ось
и ось 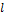 одинаково направлены и отрицательное число
одинаково направлены и отрицательное число  если вектор
если вектор 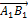 и ось
и ось 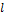 противоположно направлены (см. рис. 2).
противоположно направлены (см. рис. 2).
Если точки 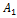 и
и 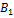 совпадают (
совпадают ( 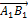 =
= 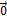 ), то проекция вектора
), то проекция вектора 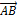 равна 0.
равна 0.
Проекция вектора 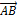 на ось
на ось 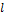 обозначается так:
обозначается так:  . Если
. Если 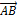 =
= 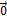 или
или 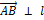 , то
, то  = 0.
= 0.
Рассмотрим основные свойства проекции:
Свойство 1. Проекция вектора  на ось
на ось 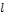 равна произведению модуля вектора
равна произведению модуля вектора  на косинус угла
на косинус угла 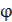 между вектором и осью, т.е.
между вектором и осью, т.е.
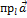 = |
= |  |
| 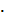 cos
cos 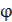 .
.
Следствие 1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если угол – прямой.
Следствие 2. Проекция равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.  (
(  +
+  +
+ 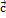 ) =
) =  +
+ 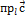 .
.
Свойство 3. При умножении вектора  на число
на число 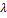 его проекция на ось также умножается на это число, т.е.
его проекция на ось также умножается на это число, т.е.  (
( 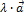 ) =
) = 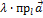 .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Дата: 2019-12-10, просмотров: 341.