Система m линейных уравнений с n неизвестными называется системой линейных однородных уравнений, если все их свободные члены равны нулю.
Такая система имеет вид:
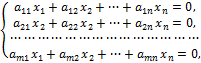
или в матричной форме А 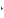 Х = 0.
Х = 0.
Однородная система всегда совместна (r(A) = r(Ã)), она имеет нулевое (тривиальное) решение х1 = х2 = … = х n = 0.
Если в системе m = n, а её определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы Крамера. Ненулевые решение возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю.
Следовательно, справедливы следующие теоремы:
Теорема 1. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r её основной матрицы был меньше числа n неизвестных, т.е. r<n.
Теорема 2. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы её определитель D был равен нулю, т.е. D = 0.
Положим,r = r(A). Пусть общее решение однородной системы записано в виде
Х = 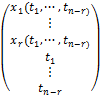
где х1, …, xr – главные переменные; t1, …, tn-r – значения свободных переменных xr+1, …, xn. Выберем n – r решений системы, полученных из общего решения следующим образом: одно из значений свободных переменных полагается равным 1, а остальные – равными 0:
Х1 = 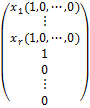 ,
,
Х2 =, 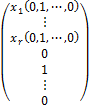 … ,
… ,
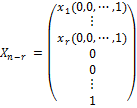 .
.
Эти решения образуют нормальную фундаментальную систему решений однородной системы, которые обладают следующим свойством:
Любое решение Х однородной системы может быть единственным образом представлено в виде:
X = α1 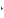 X1 + α2
X1 + α2 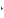 X2 + … + αn-r
X2 + … + αn-r  Xn-r,
Xn-r,
где α1, α2, …, αn-r– некоторые числа.
Любой набор из n-rрешений системы, обладающих указанным свойством, называется фундаментальной системой решений однородной системы.
Общее решение неоднородной системы линейных уравнений А  X = B, может быть представлено в виде суммы общего решения однородной системы АХ = 0 и какого-то одного (частного) решения неоднородной системы.
X = B, может быть представлено в виде суммы общего решения однородной системы АХ = 0 и какого-то одного (частного) решения неоднородной системы.
Пример 6. Найти общее решение и фундаментальную систему решений для однородной системы линейных уравнений:
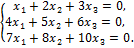
Решение. Приведём матрицу системы к ступенчатому виду:

Так как r(A) = r(Ã) = 3 = n, то система определенна и имеет единственное тривиальное нулевое решение х1 = х2 = х3 = 0.
Ответ. Общее решение: (0; 0; 0); фундаментальной системы решений нет.
Пример 7. Найти общее решение и фундаментальную систему решений для однородной системы линейных уравнений:
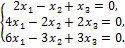
Решение. Приведём матрицу системы к ступенчатому виду:
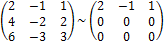
Так как r(A) = r(Ã) = 1 < 3 =n, то система неопределенна. В качестве главного переменного можно выбрать одну из переменных.
2х1 – х2 + х3 = 0 =>х3 = х2 – 2х1
Пусть х1 = t1, x2 = t2. Тогда, общее решение системы:
(t1; t2; t2 – 2t1) = t1 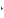 (1; 0; -2) +t2
(1; 0; -2) +t2 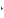 (0; 1; 1).
(0; 1; 1).
Фундаментальная система решений: {(1; 0; -2), (0; 1; 1)}.
Контрольные вопросы к главе 2
1. Привести общий вид системы линейных алгебраических уравнений.
2. В чем особенность однородных систем?
3. Что такое решение системы?
4. Из чего состоят основная и расширенная матрицы системы?
5. Что такое ранг матрицы?
6. В чем состоит суть теоремы Кронекера - Капелли?
7. Каково соотношение между числом неизвестных, числом решений и рангом системы?
8. Что такое свободные неизвестные и когда их вводят?
9. Сформулировать теорему Крамера.
10. Как вычисляются неизвестные матричным методом?
11. В чем заключается идея метода Гаусса?
12. Какие преобразования матриц называются элементарными?
13. Какие системы являются эквивалентными?
14. Как контролируются полученные результаты решения системы?
Тесты к главе 2

- При решении системы по правилу Крамера используют формулы
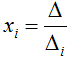
|
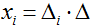
|
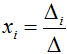
|
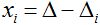
|
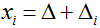
|
3. Если 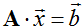 , то
, то

|
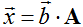
|
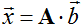
|
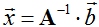
|
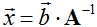
|
- Система линейных алгебраических уравнений несовместна совместна определена неопределена однородна тогда и только тогда, когда определитель решение ранг коэффициент основной матрицы равен рангу ее расширенной основной ступенчатой квадратной матрицы.
- Число векторов в фундаментальной системе решений однородной системы равно...
| рангу матрицы системы |
| числу ненулевых строк в ступенчатом виде |
| числу базисных переменных |
| числу свободных переменных |
| наивысшему порядку отличного от нуля минора |
| числу констант в общем решении |
6. Найти значение b, при котором система совместна

Ответ вписать целым числом.
Ответ введите, заполнив форму:
+ –
- Найти значение а, при котором система несовместна
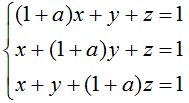
Ответ вписать целым числом.
Ответ введите, заполнив форму:
+ –
- Найти значение n, при котором система
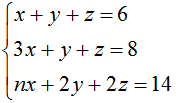
имеет бесконечно много решений. Ответ вписать целым числом.
Ответ введите, заполнив форму:
+ –
Дата: 2019-12-10, просмотров: 394.