Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные.

Пусть дана система m линейных уравнений с n неизвестными

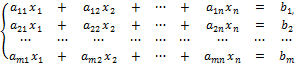
Предположим, что система совместна и не все её коэффициенты равны нулю. Пусть коэффициент 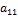 не равен нулю.

Умножая первое уравнение системы на 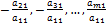 и последовательно прибавляя ко второму, третьему и т.д. уравнениям, получим эквивалентную систему.

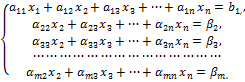
Продолжая преобразования системы, получим эквивалентную систему вида

,

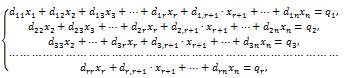где ни один из коэффициентов d_11­, d₂₂, …, d_rr не равен нулю.

Если r<n, то все члены, содержащие неизвестные с номерами большими, чем r, переносим вправо:

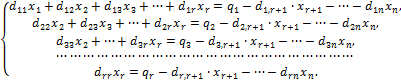
Полагая в этой системе x_r+1=c_r+1,x_r+2=c_r+2,…,x_n= c_n, получим систему r уравнений с rнеизвестными и с не равным нулю треугольным определителем. Пусть найдено её решение:

x₁ = c₁, x₂ = c₂, …, x_r = c_r. Таким образом, совокупность чисел (c₁, c₂, …, c_r, c_r+1, …, c_n) является решением системы. Так как числа c_r+1, c_r+2, …, c_n можно выбрать произвольно, то система имеет бесконечное множество решений.

Если r = n, то получится треугольная система линейных уравнений, имеющая единственное решение.

В процессе преобразований исходной системы уравнений может получиться уравнение вида 0 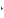x_r + 0 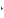x_r+1 + … + 0 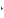x_n = q ≠ 0. Так как нельзя подобрать таких значений неизвестных, которые удовлетворяли бы этому уравнению, то система в таком случае несовместна.

На практике преобразуют обычно не систему уравнений, а её расширенную матрицу Ã.

Возможны следующие три случая, которые разберём на конкретных примерах.

1) Расширенная матрица Ã исходной системы приводится к треугольной, в которой все элементы главной диагонали отличны от нуля. В этом случае система имеет единственное решение.

Пример 3. Решить систему уравнений: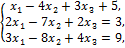

Решение. Приведём к ступенчатому (или треугольному) виду расширенную матрицу системы: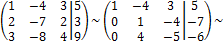  

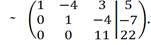
Так как r(A) = r(Ã) = 3 = n, то система совместна и определенна. Последней матрице соответствует следующая система:

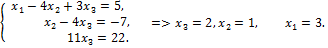
Следовательно, система имеет единственное решение (3; 1; 2).

2) Расширенная матрица Ã исходной системы приводится к собственно квазитреугольной (трапециевидной) форме. Если система совместна, то в этом случае она будет неопределенной, т.е. будет иметь бесконечное множество решений.

Пример 4. Решить систему уравнений:

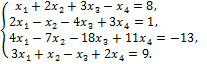
Решение. Приведём к ступенчатому виду расширенную матрицу системы

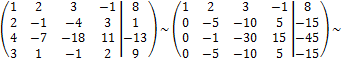
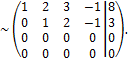
r(A) = r(Ã) = 2<4 = n, то система совместна и неопределенна. Количество главных переменных равно r(A) = 2, количество свободных переменных равно n – r(A) = 2. Выберем какой-нибудь не равный нулю минор 2-го порядка, например, минор . Его столбцы соответствуют переменным x₁ и – это будут главные переменные, а х₃ и х₄ – свободные переменные. Запишем систему уравнений соответствующую полученной расширенной матрице:

или же { .

Подставляя выражение для х₂ в первое уравнение, получим: х₁ = 2 + х₃ – х₄. Пусть х₃ = с₁, х₄ = с₂. Таким образом, общее решение системы имеет вид:

(2 + с₁ – с₂; 3 – 2с₁ + с₂; с₁; с₂).

3) В процессе преобразований строк матрицы Ã может получиться, что нулевой строке матрицы коэффициентов соответствует ненулевой элемент столбца правых частей. И этой строке соответствует уравнение

0 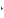x₁ + 0 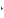x₂ + … + 0 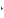x_n = b_i. Если b_i ≠ 0, то исходная система несовместна.

Пример 5. Решить систему уравнений.

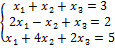
Решение. Преобразуем расширенную матрицу системы

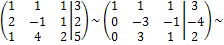
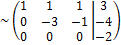
Уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = 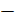2, следовательно, данная система несовместна.