Матрица А-1 называется обратной квадратной матрице А, если А  А-1= А-1
А-1= А-1  А = Е.
А = Е.
Теорема. Для того, чтобы у матрицы А существовала обратная, необходимо и достаточно, чтобы матрица А была невырожденной, т.е. чтобы её определитель был отличен от нуля. Обратная матрица единственна.
Обратную матрицу для А можно строить двумя способами.
Первый способ. Обратную матрицу для А строим по формуле.
 ,
,
где A ij – алгебраическое дополнение элемента aij матрицы А и ׀А׀ – определитель матрицы.
Матрица
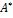 =
= 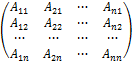
строится заменой элементов aij их алгебраическими дополнениями с последующим транспонированием. Она называется союзной матрицей к А.
Второй способ. МатрицаА-1 может быть построена с помощью элементарных преобразований. Приписываем к матрице А справа единичную матрицу Е того же порядка и вновь полученную матрицу (А׀Е) приводим к
виду (Е׀В). Тогда А-1 = В.
Уравнения вида А  Х = В и Х
Х = В и Х  А = В, где А, В, Х – матрицы, называются матричными уравнениями. Неизвестная матрица Х для первого уравнения находится по формуле Х = А-1
А = В, где А, В, Х – матрицы, называются матричными уравнениями. Неизвестная матрица Х для первого уравнения находится по формуле Х = А-1  В, а для второго – по формуле Х = В
В, а для второго – по формуле Х = В  А-1.
А-1.
Пример 12. Найти обратную матрицу к матрице
А = 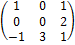
Решение. Матрица А-1 существует, т.к.׀А׀ = -6 ≠ 0.
Первый способ. Находим алгебраические дополнения Aij:
А11 = -6, А21 = 3, А31 = 0,
А12 = -2, А22 = 2, А32 = -2,
А13= 0, А23 = - 3 А33 = 0.
Тогда
А-1= 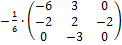
Второй способ. Строим матрицу вида (А׀Е). 
Умножим вторую строку на 1/3, третью строку на ½:
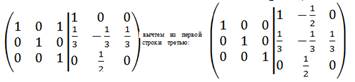
Таким образом
А-1= 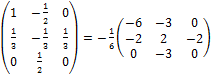 .
.
Пример 13. Решить матричное уравнение:
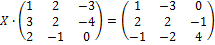
Решение.
Х  А = В => Х = В
А = В => Х = В  А-1
А-1
а) найдём определитель матрицы А:
׀А׀= 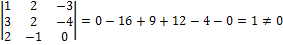
МатрицаА – невырождена, значит, существует
А-1 = 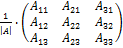 .
.
б) найдём А-1:

А-1 = 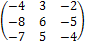
в) Найдём матрицу Х = В 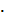 А-1
А-1
X = 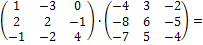
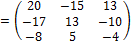
Раздел 1.6. Ранг матрицы
Рассмотрим матрицу размеров m × n
A= 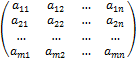
Выберем в ней произвольно k различных строк и k различных столбцов, причём 1 <k ≤ min (m, n), где min (m, n) – меньшее из чисел m и n.
Элементы, стоящие на пересечении выбранных строк и столбцов, образуют матрицу порядка k. Определитель этой матрицы называется минором порядка k матрицы А.
Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Ранг матрицы будем обозначать буквой r. Если все миноры матрицы равны нулю, ранг её считается равным нулю.
Из определения ранга матрицы получаем следующие утверждения:
1. Ранг матрицы r: 0 ≤ r ≤ min (m, n).
2. r = 0 тогда и только тогда, когда матрица является нулевой.
3. Для квадратной матрицы n-го порядка r = n тогда и только тогда, когда матрица невырожденная.
При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все миноры порядка k данной матрицы равны нулю, то все миноры более высокого порядка также равны нулю. Это следует из теоремы о разложении определителя по элементам любой строки (столбца).
Таким образом, если среди миноров порядка k данной матрицы есть отличные от нуля, а все миноры порядка k +1 равны нулю или не существуют, то r = k.
Итак, ранг матрицы может быть найден следующим образом:
Если все миноры первого порядка (элементы матрицы) равны нулю, то r = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то r = 1. В случае, когда имеется минор второго порядка, отличный от нуля, исследуют миноры третьего порядка. Так поступают до тех пор, пока не обнаружится одно из двух: либо все миноры порядка k равны нулю, либо миноры порядка k не существуют, тогда r = k – 1.
Пример 14. Найти ранг матрицы.
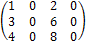
Среди миноров первого порядка этой матрицы (её элементов) есть отличный от нуля, поэтому r  0. Из элементов данной матрицы можно составить миноры второго и третьего порядка, но все они равны нулю. Следовательно, r = 1.
0. Из элементов данной матрицы можно составить миноры второго и третьего порядка, но все они равны нулю. Следовательно, r = 1.
Отметим некоторые очевидные свойства ранга матрицы:
1. Ранг матрицы, полученной из данной транспонированием, равен рангу исходной матрицы.
2. Ранг матрицы не изменится, если вычеркнуть или приписать нулевой ряд.
Можно доказать, что при элементарных преобразованиях ранг матрицы не меняется. Это следует из определения ранга матрицы и свойств определителей. С помощью элементарных преобразований матрицу можно привести к квазитреугольной форме. Ранг квазитреугольной матрицы равен r, поскольку её минор с главной диагональю а11, а22, …, а rr равен произведению а11  а22
а22  …
…  а rr ≠ 0, а все миноры более высокого порядка равны нулю (как содержание нулевые строки).
а rr ≠ 0, а все миноры более высокого порядка равны нулю (как содержание нулевые строки).
Пример 15. Найти ранг матрицы.

Решение. Применяя элементарные преобразования, получаем
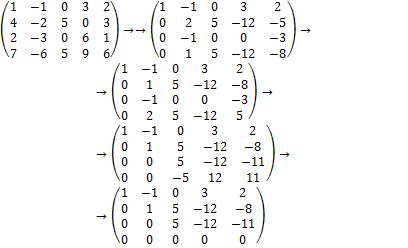
(Вторая матрица получена из первой путём поочерёдного умножения первой строки на (-4), (-2), (-7) и соответственного прибавления ко второй, третьей и четвёртой строке; поменяв местами вторую и четвёртую строки во второй матрице, получили третью матрицу; четвёртая матрица получена из третьей путём умножения второй строки на (-2) и прибавления к четвёртой строке, сложения второй и третьей строк).
Так как ранг последней матрицы равен трём, для исходной матрицы также r = 3.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).
Теорема о ранге матрицы играет особую роль при исследовании систем линейных уравнений.
Контрольные вопросы к главе 1
1. Дать определение матрицы.
2. Классификация матриц по размерам.
3. Что такое нулевая матрица?
4. Что такое единичная матрица?
5. При каких условиях матрицы считаются равными?
6. Как выполняется операция транспонирования?
7. Когда возможна операция сложения матриц и как вычисляется результат?
8. Как найти произведение матрицы на число?
9. Когда возможна операция умножения матриц?
10. Какова размерность результата умножения?
11. По какому правилу вычисляется элемент матрицы — результата при перемножении матриц?
12. Какие матрицы называются взаимно обратными?
13. У каких матриц может быть найден определитель?
14. Как вычислить определитель второго порядка?
15. Что такое минор?
16. Что является алгебраическим дополнением элемента матрицы?
17. Как вычисляется определитель n-го порядка?
18. Перечислитесвойстваопределителей.
19. Какой вид имеет определитель Вандермонда?
Тесты к главе 1
1. Начало формы
- Если матрица
 , то матрица 4A имеет вид
, то матрица 4A имеет вид
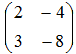
| 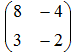
|
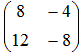
| 
|
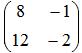
|
- Если матрицы
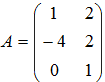 и
и 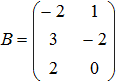 , то матрица
, то матрица
3A – 2B имеет вид
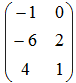
| 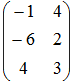
|
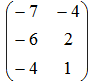
| 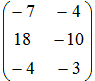
|
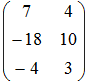
|
- Для матрицы
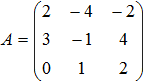 указать сумму элементов, расположенных
указать сумму элементов, расположенных
на побочной диагонали. Ответ введите, заполнив форму:
+ – 0 1 2 3 4 5 6 7 8 9
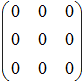
- Расставить матрицы в порядке убывания их рангов:
1. 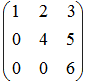
|
2. 
|
3. 
|
4. 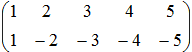
|
Введите последовательность номеров
без разделительных знаков:
- Для матриц
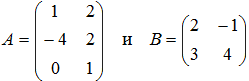 указать те операции,
указать те операции,
которые можно выполнить
| B · A |
| B · AT |
| BT · A |
| BT · AT |
| A · B |
| AT · B |
| A · BT |
| AT · BT |
| все указанные операции можно выполнить |
- Ранг матрицы A размера n × n равен
| n |
| n – 1, если матрица вырождена |
| указанных условий недостаточно для определения ранга |
| n – 1 |
| n – 1, если матрица невырождена |
Дата: 2019-12-10, просмотров: 400.