Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц А m × n = (aij) и Bm × n = (bij) называется матрицаCm × n = (cij) — такая, что cij = aij + bij (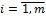 
, 
).
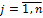Пример 3.
А =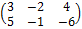 
,
B=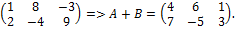 
Аналогично определяется разность матриц.
Произведением матрицы Am × n = (aij) на число α, называется матрица Bm × n = (bij) — такая, что bij = α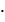 
aij ( , ).
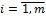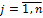Пример 4.
Матрица –А = (-1)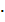 
А называется противоположной матрице А.
Разность матриц А – В можно определить так: А – В = А + (-В).
Под линейными операциями над матрицами понимают операции сложения и вычитания матриц, а также умножение матрицы на число.
Линейные операции над матрицами обладают следующими свойствами:
1. A + B = B + A;
2. A + (B + C) = (A + B) + C;
3. A + 0 = A;
4. A + (-A) = 0
5. 1 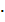A = A;
6. α 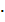(A + B) = αA + αB;
7. (α + β) 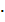A = αA + βA;
8. α 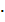(βA) = (αβ) A;
где А, В, С – матрицы одних и тех же размеров; 0 – нулевая матрица, (-А) – матрица, противоположная матрице А; α‚ β – любые действительные числа.
Элементарными преобразованиями матрицы называются следующие операции:
1. Перестановка местами двух параллельных рядов матрицы.
2. Умножение всех элементов ряда матрицы на число, отличное от нуля.
3. Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Матрица В, полученная из матрицы А с помощью элементарных преобразований называется эквивалентной матрице А (обозначается В ~ А).
Операция умножения двух матриц вводится только для случая, когда матрица А согласована с матрицей В. Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. Отметим следующее:
1. Из согласованности матрицы А с матрицей В не следует согласованность матрицы В с матрицей А;
2. Если А и В – квадратные матрицы одного порядка, то они взаимно согласованы (А согласована с В, В согласована с А).
Произведением (умножением) матрицы А m × n на матрицу В n × k называется матрица С m × k, такая что
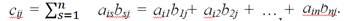
Замечание. Из того, что матрицу А можно умножить на матрицу В, не следует, что матрицу В можно умножать на А (т.к. из согласованности А с В не следует согласованность В с А).
Пример 4.
Пусть
.
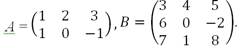Найти произведение АВ и ВА (если это возможно).
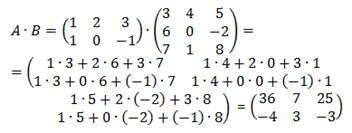
Произведение ВА не существует, т.к. число столбцов матрицы В не совпадает с числом строк матрицы А (3≠2).
Пример 5. Даны две матрицы второго порядка
А =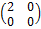 
, B=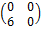 
.
Найти произведение АВ и ВА.
,
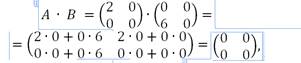
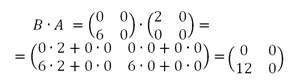следовательно, АВ ≠ ВА.
Если для матриц А и В определены произведения АВ и ВА, то не всегда АВ=ВА. В случае, когда АВ=ВА, матрицы А и В называются перестановочными, или коммутативными.
Легко видеть, что
А 
Е = Е А = А,
А 
О = О А = О,
т.е. единичная и нулевая матрицы перестановочны с произвольными матрицами.
Умножение матриц обладает следующими свойствами:
1. А (В С) = (А В) С;
2. А (В + С) = АВ + АС;
3. (А + В) С = АС + ВС;
4. α(АВ) = (αА) В.
Для операции транспортирования верны свойства:
1. (А + В)Т = АТ + ВТ;
2. (АВ)Т = ВТ АТ.
Раздел 1.3. Определители
Определителем квадратной матрицы А называется число D, которое ставится в соответствие данной матрице и обозначается
D = ׀A׀=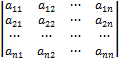 
.
По определению:
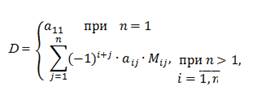
где aij – элементы i-ой строки определителя; Mij – определитель порядка n -1, получающийся из D вычёркиванием i-ой строки и j-того столбца.
Числа Mij называются минорами элементов aij. Числа Aij = (-1)i + j Mij называются алгебраическими дополнениями элементов aij.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов некоторого ряда на алгебраические дополнения этих элементов.
Такая сумма называется разложением определителя по элементам соответствующего ряда.
Определители обладают следующими свойствами.
Свойство 1. Строки и столбцы равноправны. Другими словами, определитель транспонированной матрицы равен определителю исходной.
Свойство 2.Перестановка двух параллельных рядов определителя меняет его знак на противоположный.
Свойство 3. Определитель с двумя равными или пропорциональными параллельными рядами равен нулю.
Свойство 4. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
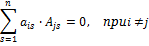
Замечание. Объединяя результат теоремы Лапласа и свойство 4, получаем:
.
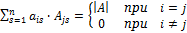Свойство 5. Если все элементы какой-либо строки (столбца) матрицы умножить на число λ, то её определитель умножится на это число λ.
Свойство 6. Определитель равен нулю, если все элементы некоторого ряда равны нулю.
Свойство 7. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:
=
= 
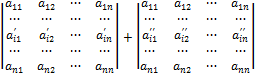
Свойство 8 (элементарные преобразования определителя). Прибавление к элементам ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число, не изменяет определителя.
Свойство 9. Определитель треугольной матрицы равен произведению элементов главной диагонали.
Свойство 10.Определитель произведения матриц равен произведению их определителей: ׀C׀ = ׀A׀ ׀B׀, где C = A B; A и B– матрицыn-го порядка.
Замечание. Из свойства 10 следует, что даже если AB ≠ BA, то ׀AB׀=BA׀.
Дата: 2019-12-10, просмотров: 256.
