Р. Б. Г у л и е в
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Учебное пособие
Санкт-Петербург
2017
УДК
ББК
Гулиев
Рецензенты:
ИвановВ.А., Санкт-Петербургский государственный университет, профессор кафедры оптики, доктор физико-математических наук, профессор;
Майоров Е.Е., Университет при МПА ЕврАзЭС, заведующий кафедрой математики и информационных технологий, кандидат экономических наук, доцент
Гулиев Р.Б. Элементы линейной алгебры: учебное пособие. – СПб.: Университет при МПА ЕврАзЭС, 2017. ___ с.
Учебное пособие по линейной алгебре предназначено для студентов, обучающихся экономическим специальностям. Оно предназначено в помощь студентам всех форм обучения при изучении учебной дисциплины «Математика», которая входит в федеральный компонент общепрофессиональных дисциплин, предусмотренных государственным образовательным стандартом высшего образования. В пособие включены темы, изучаемые студентами Университета при МПА ЕврАзЭС во втором семестре. Пособие состоит из пяти глав: «Матрицы и определители», «Cистемы линейных уравнений», «Элементы векторной алгебры», «Линейные пространства», «Квадратичные формы». В нем рассматриваются типовые задачи и приводятся их решения с объяснениями. Теоретический материал сопровождается иллюстрациями.
Данное учебное пособие является дополненным и переработанным.
© Гулиев Р.Б., 2017
© Университет при МПА ЕврАзЭС, 2017
ОГЛАВЛЕНИЕ
| Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 5 |
| Глава I .Матрицы и определители . . . . . . . . . . . . . . . . . . . . . . . | 8 |
| Раздел 1.1.Основныеопределения . . . . . . . . . . . . | |
| Раздел 1.2. Действия над матрицами . . . . . . . . . . . . ……… | |
| Раздел 1.3. Определители . . . . . . . . . . . | |
| Раздел 1.4. Вычисление определителей . . . . . . . . . . . | |
| Раздел 1.5. Обратная матрица. Матричные уравнения . . . | |
| Раздел 1.6. Ранг матрицы . . . . . . . . . . | |
| Глава II .Системы линейных уравнений . . . . . . . . . . . . . . . . . . | 34 |
| Раздел 2.1. Основные понятия и определения . . . . . . . . . . . | |
| Раздел 2.2. Исследование систем линейных уравнений. Теорема Кронекера-Капелли . . . . . . . . . . . | |
| Раздел 2.3. Метод обратной матрицы и формулы Крамера . . . . . . . . . . . | |
| Раздел 2.4. Метод последовательного исключения неизвестных. Метод Гаусса . . . . . . . . . . | |
| Раздел 2.5.Системы линейных однородных уравнений. Фундаментальная система решений . . | |
| Глава III. Элементы векторной алгебры. . . . . . . . . . . . . . . . . . | 53 |
| Раздел 3.1. Векторы. Основные понятия . . . . . . . . . | |
| Раздел 3.2. Разложение вектора по ортам координатных осей . . . . . . . . . . | |
| Раздел 3.3. Скалярное произведение векторов . . . . . . . . . . | |
| Раздел 3.4. Векторное произведение векторов и его свойства . . . . . . . . . . | |
| Раздел 3.5. Смешанное произведение векторов . | |
| Глава IV. Линейные пространства . . . . . . . . . . . . | 67 |
| Раздел 4.1.n-мерный вектор и векторное пространство . . | |
| Раздел 4.2. Линейная зависимость и линейная независимость векторов . . . . . . . . . . . | |
| Раздел 4.3. Преобразование координат при переходе к новому базису . . . . . . . . . . . | |
| Раздел 4.4. Евклидово пространство . . . . . . . . . . | |
| Раздел 4.5. Линейные операторы . . | |
| Раздел 4.6. Собственные векторы и собственные значения линейного оператора . . . . . . . . . | |
| Глава V .Квадратичные формы. . . . . . . . . . 96 | |
| Раздел 5.1.Квадратичные формы и их матрицы . | |
| Раздел 5.2. Канонический вид квадратичной формы . . . . | |
| Раздел 5.3. Классификация квадратичных форм. Знакоопределение формы . . . . . . . . . . . | |
| Заключение. . . . . . . . . . . . . | 111 |
| Список литературы. . . . . . . . . . . . . | 112 |
Предисловие
Учебное пособие «Элементы линейной алгебры» предназначено в помощь студентам всех форм обучения при изучении учебной дисциплины «Математика», которая входит в федеральный компонент общепрофессиональных дисциплин, предусмотренных государственным образовательным стандартом высшего профессионального образования.
Материал, изложенный в предлагаемом учебном пособии, охватывает основные разделы дисциплины «Линейная алгебра», которая является составной частью учебной дисциплины «Математика», изучаемой в экономических вузах.
В первой и во второй главах данного учебного пособия определяются базовые понятия линейной алгебры такие, как матрицы, определители и системы линейных уравнений. Третья глава посвящена векторной алгебре. Линейные пространства и квадратичные формы представлены в четвёртой и пятой главах.
В целях более эффективного усвоения материала в учебном пособии для ряда понятий приведена геометрическая или механическая интерпретация. Каждое вводимое понятие сопровождается подробно разобранными примерами и иллюстрациями, что позволяет использовать учебное пособие для самостоятельного изучения материала обучающимися. Пособие можно рекомендовать не только для использования при профессиональной подготовке студентов очно-заочной и заочной форм обучения, но и для дистанционного обучения.
Структура и содержание учебного пособия «Элементы линейной алгебры» соответствуют государственному образовательному стандарту и примерной программе учебной дисциплины, изучаемой обучающимися экономическим специальностям.
Раздел 1.3. Определители
Определителем квадратной матрицы А называется число D, которое ставится в соответствие данной матрице и обозначается
D = ׀A׀= 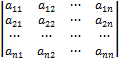 .
.
По определению:
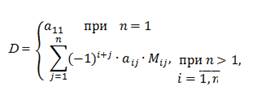
где aij – элементы i-ой строки определителя; Mij – определитель порядка n -1, получающийся из D вычёркиванием i-ой строки и j-того столбца.
Числа Mij называются минорами элементов aij. Числа Aij = (-1)i + j  Mij называются алгебраическими дополнениями элементов aij.
Mij называются алгебраическими дополнениями элементов aij.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов некоторого ряда на алгебраические дополнения этих элементов.
Такая сумма называется разложением определителя по элементам соответствующего ряда.
Определители обладают следующими свойствами.
Свойство 1. Строки и столбцы равноправны. Другими словами, определитель транспонированной матрицы равен определителю исходной.
Свойство 2.Перестановка двух параллельных рядов определителя меняет его знак на противоположный.
Свойство 3. Определитель с двумя равными или пропорциональными параллельными рядами равен нулю.
Свойство 4. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
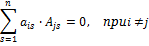
Замечание. Объединяя результат теоремы Лапласа и свойство 4, получаем:
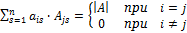 .
.
Свойство 5. Если все элементы какой-либо строки (столбца) матрицы умножить на число λ, то её определитель умножится на это число λ.
Свойство 6. Определитель равен нулю, если все элементы некоторого ряда равны нулю.
Свойство 7. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:
 =
=
= 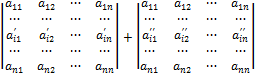
Свойство 8 (элементарные преобразования определителя). Прибавление к элементам ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число, не изменяет определителя.
Свойство 9. Определитель треугольной матрицы равен произведению элементов главной диагонали.
Свойство 10.Определитель произведения матриц равен произведению их определителей: ׀C׀ = ׀A׀  ׀B׀, где C = A
׀B׀, где C = A  B; A и B– матрицыn-го порядка.
B; A и B– матрицыn-го порядка.
Замечание. Из свойства 10 следует, что даже если AB ≠ BA, то ׀AB׀=BA׀.
Решение.
Х  А = В => Х = В
А = В => Х = В  А-1
А-1
а) найдём определитель матрицы А:
׀А׀= 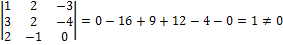
МатрицаА – невырождена, значит, существует
А-1 = 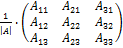 .
.
б) найдём А-1:

А-1 = 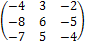
в) Найдём матрицу Х = В 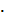 А-1
А-1
X = 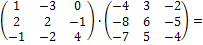
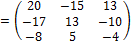
Раздел 1.6. Ранг матрицы
Рассмотрим матрицу размеров m × n
A= 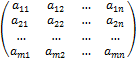
Выберем в ней произвольно k различных строк и k различных столбцов, причём 1 <k ≤ min (m, n), где min (m, n) – меньшее из чисел m и n.
Элементы, стоящие на пересечении выбранных строк и столбцов, образуют матрицу порядка k. Определитель этой матрицы называется минором порядка k матрицы А.
Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Ранг матрицы будем обозначать буквой r. Если все миноры матрицы равны нулю, ранг её считается равным нулю.
Из определения ранга матрицы получаем следующие утверждения:
1. Ранг матрицы r: 0 ≤ r ≤ min (m, n).
2. r = 0 тогда и только тогда, когда матрица является нулевой.
3. Для квадратной матрицы n-го порядка r = n тогда и только тогда, когда матрица невырожденная.
При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все миноры порядка k данной матрицы равны нулю, то все миноры более высокого порядка также равны нулю. Это следует из теоремы о разложении определителя по элементам любой строки (столбца).
Таким образом, если среди миноров порядка k данной матрицы есть отличные от нуля, а все миноры порядка k +1 равны нулю или не существуют, то r = k.
Итак, ранг матрицы может быть найден следующим образом:
Если все миноры первого порядка (элементы матрицы) равны нулю, то r = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то r = 1. В случае, когда имеется минор второго порядка, отличный от нуля, исследуют миноры третьего порядка. Так поступают до тех пор, пока не обнаружится одно из двух: либо все миноры порядка k равны нулю, либо миноры порядка k не существуют, тогда r = k – 1.
Пример 14. Найти ранг матрицы.
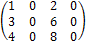
Среди миноров первого порядка этой матрицы (её элементов) есть отличный от нуля, поэтому r 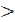 0. Из элементов данной матрицы можно составить миноры второго и третьего порядка, но все они равны нулю. Следовательно, r = 1.
0. Из элементов данной матрицы можно составить миноры второго и третьего порядка, но все они равны нулю. Следовательно, r = 1.
Отметим некоторые очевидные свойства ранга матрицы:
1. Ранг матрицы, полученной из данной транспонированием, равен рангу исходной матрицы.
2. Ранг матрицы не изменится, если вычеркнуть или приписать нулевой ряд.
Можно доказать, что при элементарных преобразованиях ранг матрицы не меняется. Это следует из определения ранга матрицы и свойств определителей. С помощью элементарных преобразований матрицу можно привести к квазитреугольной форме. Ранг квазитреугольной матрицы равен r, поскольку её минор с главной диагональю а11, а22, …, а rr равен произведению а11 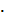 а22
а22 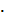 …
… 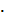 а rr ≠ 0, а все миноры более высокого порядка равны нулю (как содержание нулевые строки).
а rr ≠ 0, а все миноры более высокого порядка равны нулю (как содержание нулевые строки).
Пример 15. Найти ранг матрицы.

Решение. Применяя элементарные преобразования, получаем
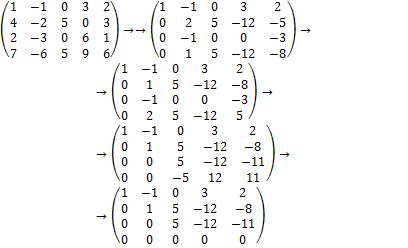
(Вторая матрица получена из первой путём поочерёдного умножения первой строки на (-4), (-2), (-7) и соответственного прибавления ко второй, третьей и четвёртой строке; поменяв местами вторую и четвёртую строки во второй матрице, получили третью матрицу; четвёртая матрица получена из третьей путём умножения второй строки на (-2) и прибавления к четвёртой строке, сложения второй и третьей строк).
Так как ранг последней матрицы равен трём, для исходной матрицы также r = 3.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).
Теорема о ранге матрицы играет особую роль при исследовании систем линейных уравнений.
Контрольные вопросы к главе 1
1. Дать определение матрицы.
2. Классификация матриц по размерам.
3. Что такое нулевая матрица?
4. Что такое единичная матрица?
5. При каких условиях матрицы считаются равными?
6. Как выполняется операция транспонирования?
7. Когда возможна операция сложения матриц и как вычисляется результат?
8. Как найти произведение матрицы на число?
9. Когда возможна операция умножения матриц?
10. Какова размерность результата умножения?
11. По какому правилу вычисляется элемент матрицы — результата при перемножении матриц?
12. Какие матрицы называются взаимно обратными?
13. У каких матриц может быть найден определитель?
14. Как вычислить определитель второго порядка?
15. Что такое минор?
16. Что является алгебраическим дополнением элемента матрицы?
17. Как вычисляется определитель n-го порядка?
18. Перечислитесвойстваопределителей.
19. Какой вид имеет определитель Вандермонда?
Тесты к главе 1
1. Начало формы
- Если матрица
 , то матрица 4A имеет вид
, то матрица 4A имеет вид
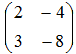
| 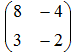
|
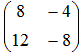
| 
|
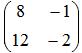
|
- Если матрицы
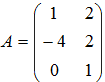 и
и 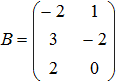 , то матрица
, то матрица
3A – 2B имеет вид
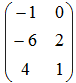
| 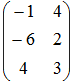
|
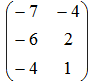
| 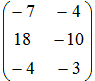
|
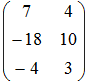
|
- Для матрицы
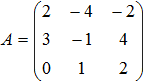 указать сумму элементов, расположенных
указать сумму элементов, расположенных
на побочной диагонали. Ответ введите, заполнив форму:
+ – 0 1 2 3 4 5 6 7 8 9
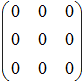
- Расставить матрицы в порядке убывания их рангов:
1. 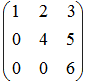
|
2. 
|
3. 
|
4. 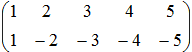
|
Введите последовательность номеров
без разделительных знаков:
- Для матриц
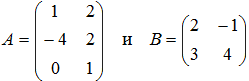 указать те операции,
указать те операции,
которые можно выполнить
| B · A |
| B · AT |
| BT · A |
| BT · AT |
| A · B |
| AT · B |
| A · BT |
| AT · BT |
| все указанные операции можно выполнить |
- Ранг матрицы A размера n × n равен
| n |
| n – 1, если матрица вырождена |
| указанных условий недостаточно для определения ранга |
| n – 1 |
| n – 1, если матрица невырождена |
Тесты к главе 2

- При решении системы по правилу Крамера используют формулы
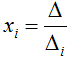
|
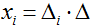
|
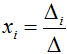
|
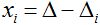
|
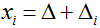
|
3. Если 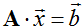 , то
, то

|
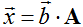
|
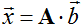
|
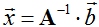
|
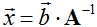
|
- Система линейных алгебраических уравнений несовместна совместна определена неопределена однородна тогда и только тогда, когда определитель решение ранг коэффициент основной матрицы равен рангу ее расширенной основной ступенчатой квадратной матрицы.
- Число векторов в фундаментальной системе решений однородной системы равно...
| рангу матрицы системы |
| числу ненулевых строк в ступенчатом виде |
| числу базисных переменных |
| числу свободных переменных |
| наивысшему порядку отличного от нуля минора |
| числу констант в общем решении |
6. Найти значение b, при котором система совместна

Ответ вписать целым числом.
Ответ введите, заполнив форму:
+ –
- Найти значение а, при котором система несовместна
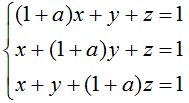
Ответ вписать целым числом.
Ответ введите, заполнив форму:
+ –
- Найти значение n, при котором система
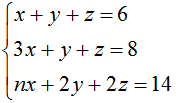
имеет бесконечно много решений. Ответ вписать целым числом.
Ответ введите, заполнив форму:
+ –
Раздел 3.1. Векторы. Основные понятия
Вектор – это направленный отрезок. Если А – начало вектора, а В – его конец, то вектор обозначается 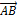 или
или  . Вектор
. Вектор 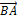 называется противоположным вектору
называется противоположным вектору 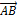 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , обозначается -
, обозначается -  .
.
Длиной или модулем вектора 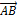 называется длина отрезка и обозначается |
называется длина отрезка и обозначается | 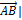 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 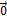 . Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором и обозначается через
. Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором и обозначается через 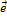 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается 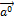 .
.
Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записываются
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записываются  ||
||  .
.
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора  и
и  называются равными (
называются равными (  =
=  ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трёх векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Для суммы двух векторов есть правило треугольника, а также правило параллелограмма.
Произведением вектора  на число
на число 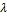 называется вектор
называется вектор 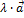 или (
или ( 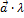 ),который имеет длину |
),который имеет длину | 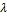 |
| 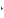 |
|  |, коллинеарен вектору
|, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если
, если 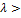 0 и противоположное направление, если
0 и противоположное направление, если 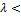 0.
0.
Из определения произведения вектора на число следуют свойства этого произведения:
1) если  =
= 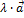 , то
, то  ||
||  . Наоборот, если
. Наоборот, если  ||
||  , (
, (  ≠
≠ 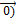 ,то при некотором
,то при некотором 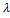 верно равенство
верно равенство  =
= 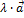 ;
;
2)  = |
= |  |
|  , т.е. каждый вектор равен произведению его модуля на орт.
, т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1. 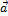 +
+ 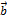 =
= 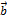 +
+ 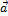 ,
,
2. ( 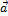 +
+ 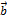 ) +
) + 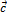 =
= 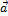 +(
+( 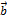 +
+ 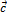 ),
),
3. 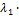 (
( 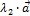 ) =
) = 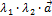
4. 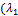 +
+ 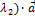 =
= 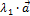 +
+ 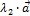 ,
,
5. 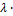 (
( 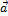 +
+ 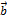 ) =
) =  +
+  .
.
Пусть в пространстве задана ось 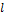 . Проекцией точки М на ось
. Проекцией точки М на ось 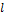 называется основание
называется основание 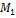 перпендикуляра
перпендикуляра 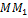 , опушенного из точки на ось (см. рис. 1)
, опушенного из точки на ось (см. рис. 1)

Проекцией вектора 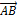 на ось
на ось 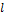 называется положительное число
называется положительное число 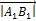 , если вектор
, если вектор 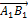 и ось
и ось 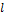 одинаково направлены и отрицательное число
одинаково направлены и отрицательное число  если вектор
если вектор 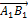 и ось
и ось 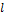 противоположно направлены (см. рис. 2).
противоположно направлены (см. рис. 2).
Если точки 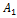 и
и 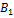 совпадают (
совпадают ( 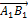 =
= 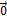 ), то проекция вектора
), то проекция вектора 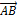 равна 0.
равна 0.
Проекция вектора 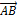 на ось
на ось 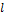 обозначается так:
обозначается так:  . Если
. Если 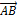 =
= 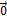 или
или 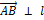 , то
, то  = 0.
= 0.
Рассмотрим основные свойства проекции:
Свойство 1. Проекция вектора  на ось
на ось 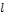 равна произведению модуля вектора
равна произведению модуля вектора  на косинус угла
на косинус угла 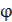 между вектором и осью, т.е.
между вектором и осью, т.е.
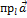 = |
= |  |
| 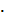 cos
cos 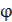 .
.
Следствие 1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если угол – прямой.
Следствие 2. Проекция равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.  (
(  +
+  +
+ 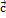 ) =
) =  +
+ 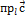 .
.
Свойство 3. При умножении вектора  на число
на число 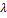 его проекция на ось также умножается на это число, т.е.
его проекция на ось также умножается на это число, т.е.  (
( 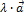 ) =
) = 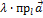 .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Тесты к главе 3
1.Чему равно скалярное произведение двух векторов, если длина первого равна 1, длина второго – 2, а угол между векторами — 60⁰?
a) 1;
b) 2;
с) 0.5.
2. Скалярное произведение двух векторов равно 0. Чему равен угол между векторами, еслидлина первого вектора -7, а второго -9?
a) 63;
b) 0⁰;
с) 90⁰.
3. Длина вектора равна 3 см. Чему равен скалярный квадрат вектора ?
a) 1;
b) 3;
с) 9.
4. Чему равно скалярное произведение двух векторов, если координаты первого {2; 1}, а координаты второго{1; 2} ?
a) 0;
b) 6;
с) 4.
5. Перпендикулярны ли два вектора, если координаты первого – {4; 2}, а координаты второго {-2; 4}?
a) нет;
b) да;
с) недостаточно данных.
Тесты к главе 4
- Для того чтобы число λ было собственным вектором собственным подпространством векторным пространством собственным значением линейного
оператора А, необходимо и достаточно, чтобы оно являлось степенью корнем значением элементом характеристического многочлена 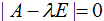 ,
,
где А – матрица оператора, а Е – обратная матрица матрица единичная матрица нулевая матрица той же размерности.
- Множество всех собственных значений называется
| рангом |
| спектром |
| следом |
| порядком |
| характером |
| определителем |
- Если
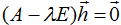 , то для линейного оператора с матрицей А
, то для линейного оператора с матрицей А
вектор 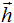 является
является
| направляющим |
| присоединенным |
| собственным |
| ортогональным |
| базисным |
| проекцией |
- Если
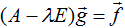 , где – присоединенный вектор i-го порядка к собственному вектору
, где – присоединенный вектор i-го порядка к собственному вектору 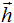 , то вектор
, то вектор 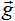 является
является
| нулевым вектором |
| собственным вектором |
присоединенным вектором (i–1)-го порядка к собственному вектору 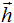
|
тоже присоединенным вектором i-го порядка к собственному вектору 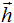
|
присоединенным вектором (i+1)-го порядка к собственному вектору 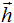
|
вектором, коллинеарным вектору 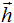
|
4. Собственные векторы линейного оператора, соответствующие различным собственным значениям, непременно являются
| равными |
| попарно различными |
| базисом в пространстве, где действует оператор |
| попарно ортогональными |
| линейно зависимыми |
| линейно независимыми |
- Найти значение а, при котором
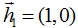 и
и 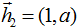 являются базисом
являются базисом
из собственных векторов линейного оператора, заданного матрицей 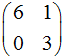
Ответ введите, заполнив форму:
+ –
- Найти собственные значения линейного оператора, заданного
матрицей 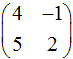 . В качестве ответа выбрать их сумму.
. В качестве ответа выбрать их сумму.
Введите ответ: 0 1 2 3 4 5 6 7 8 9 10
- Одно из собственных значений линейного оператора, заданного
матрицей, 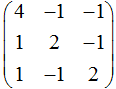 равно 2.
равно 2.
В ответе выбрать другое собственное значение.
Введите ответ:
0 1 2 3 4 5 6 7 8 9 10
Глава 5. Квадратичные формы
Список литературы
1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979.
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 2000.
3. Боревич З.И. Определители и матрицы. – М.: Наука, 1988.
4. Высшая математика для экономистов: Учебник для вузов. Под редакцией Н.Ш. Кремера. – М.: ЮНИТИ - ДАНА, 2007.
5. Гусак А.А. Высшая математика. – Мн.: ТетраСистемс, 1998.
6. Данько П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1999.
7. Ефимов Н.В. Квадратичные формы. Матрицы. – М.: Наука, 1975.
8. Кострыкин А.И. Введение в алгебру. – М.: Наука, 1977.
9. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. – М.: Дело, 2003.
10. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1975.
11. Письменный Д.Т. Конспект лекций по высшей математике. – М.: Айрис Пресс, 2010.
12. Сборник задач по высшей математике для экономистов: Учебное пособие. Под редакцией В.И. Ермакова. – М.: ИНФРА-М, 2004.
13. Березина Н.А.Линейная алгебра. Конспект лекций, Ильин В.А., Позняк Э.Г. Линейная Алгебра. [Электронный ресурс] URL: http://mexalib.com/
Р. Б. Г у л и е в
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Учебное пособие
Санкт-Петербург
2017
УДК
ББК
Гулиев
Рецензенты:
ИвановВ.А., Санкт-Петербургский государственный университет, профессор кафедры оптики, доктор физико-математических наук, профессор;
Майоров Е.Е., Университет при МПА ЕврАзЭС, заведующий кафедрой математики и информационных технологий, кандидат экономических наук, доцент
Гулиев Р.Б. Элементы линейной алгебры: учебное пособие. – СПб.: Университет при МПА ЕврАзЭС, 2017. ___ с.
Учебное пособие по линейной алгебре предназначено для студентов, обучающихся экономическим специальностям. Оно предназначено в помощь студентам всех форм обучения при изучении учебной дисциплины «Математика», которая входит в федеральный компонент общепрофессиональных дисциплин, предусмотренных государственным образовательным стандартом высшего образования. В пособие включены темы, изучаемые студентами Университета при МПА ЕврАзЭС во втором семестре. Пособие состоит из пяти глав: «Матрицы и определители», «Cистемы линейных уравнений», «Элементы векторной алгебры», «Линейные пространства», «Квадратичные формы». В нем рассматриваются типовые задачи и приводятся их решения с объяснениями. Теоретический материал сопровождается иллюстрациями.
Данное учебное пособие является дополненным и переработанным.
© Гулиев Р.Б., 2017
© Университет при МПА ЕврАзЭС, 2017
ОГЛАВЛЕНИЕ
| Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 5 |
| Глава I .Матрицы и определители . . . . . . . . . . . . . . . . . . . . . . . | 8 |
| Раздел 1.1.Основныеопределения . . . . . . . . . . . . | |
| Раздел 1.2. Действия над матрицами . . . . . . . . . . . . ……… | |
| Раздел 1.3. Определители . . . . . . . . . . . | |
| Раздел 1.4. Вычисление определителей . . . . . . . . . . . | |
| Раздел 1.5. Обратная матрица. Матричные уравнения . . . | |
| Раздел 1.6. Ранг матрицы . . . . . . . . . . | |
| Глава II .Системы линейных уравнений . . . . . . . . . . . . . . . . . . | 34 |
| Раздел 2.1. Основные понятия и определения . . . . . . . . . . . | |
| Раздел 2.2. Исследование систем линейных уравнений. Теорема Кронекера-Капелли . . . . . . . . . . . | |
| Раздел 2.3. Метод обратной матрицы и формулы Крамера . . . . . . . . . . . | |
| Раздел 2.4. Метод последовательного исключения неизвестных. Метод Гаусса . . . . . . . . . . | |
| Раздел 2.5.Системы линейных однородных уравнений. Фундаментальная система решений . . | |
| Глава III. Элементы векторной алгебры. . . . . . . . . . . . . . . . . . | 53 |
| Раздел 3.1. Векторы. Основные понятия . . . . . . . . . | |
| Раздел 3.2. Разложение вектора по ортам координатных осей . . . . . . . . . . | |
| Раздел 3.3. Скалярное произведение векторов . . . . . . . . . . | |
| Раздел 3.4. Векторное произведение векторов и его свойства . . . . . . . . . . | |
| Раздел 3.5. Смешанное произведение векторов . | |
| Глава IV. Линейные пространства . . . . . . . . . . . . | 67 |
| Раздел 4.1.n-мерный вектор и векторное пространство . . | |
| Раздел 4.2. Линейная зависимость и линейная независимость векторов . . . . . . . . . . . | |
| Раздел 4.3. Преобразование координат при переходе к новому базису . . . . . . . . . . . | |
| Раздел 4.4. Евклидово пространство . . . . . . . . . . | |
| Раздел 4.5. Линейные операторы . . | |
| Раздел 4.6. Собственные векторы и собственные значения линейного оператора . . . . . . . . . | |
| Глава V .Квадратичные формы. . . . . . . . . . 96 | |
| Раздел 5.1.Квадратичные формы и их матрицы . | |
| Раздел 5.2. Канонический вид квадратичной формы . . . . | |
| Раздел 5.3. Классификация квадратичных форм. Знакоопределение формы . . . . . . . . . . . | |
| Заключение. . . . . . . . . . . . . | 111 |
| Список литературы. . . . . . . . . . . . . | 112 |
Предисловие
Учебное пособие «Элементы линейной алгебры» предназначено в помощь студентам всех форм обучения при изучении учебной дисциплины «Математика», которая входит в федеральный компонент общепрофессиональных дисциплин, предусмотренных государственным образовательным стандартом высшего профессионального образования.
Материал, изложенный в предлагаемом учебном пособии, охватывает основные разделы дисциплины «Линейная алгебра», которая является составной частью учебной дисциплины «Математика», изучаемой в экономических вузах.
В первой и во второй главах данного учебного пособия определяются базовые понятия линейной алгебры такие, как матрицы, определители и системы линейных уравнений. Третья глава посвящена векторной алгебре. Линейные пространства и квадратичные формы представлены в четвёртой и пятой главах.
В целях более эффективного усвоения материала в учебном пособии для ряда понятий приведена геометрическая или механическая интерпретация. Каждое вводимое понятие сопровождается подробно разобранными примерами и иллюстрациями, что позволяет использовать учебное пособие для самостоятельного изучения материала обучающимися. Пособие можно рекомендовать не только для использования при профессиональной подготовке студентов очно-заочной и заочной форм обучения, но и для дистанционного обучения.
Структура и содержание учебного пособия «Элементы линейной алгебры» соответствуют государственному образовательному стандарту и примерной программе учебной дисциплины, изучаемой обучающимися экономическим специальностям.
Глава I . МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Раздел 1.1. Основные определения
Матрицей размера m × n называется прямоугольная таблица, которую будем обозначать
A= 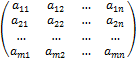 .
.
Элементы матрицы 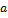 ij, где i =
ij, где i = 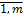 (т.е. i = 1, 2, 3, …, m), j =
(т.е. i = 1, 2, 3, …, m), j =  (т.е. j = 1, 2, 3, …n), образуют горизонтальные ряды – строки и вертикальные ряды – столбцы.
(т.е. j = 1, 2, 3, …n), образуют горизонтальные ряды – строки и вертикальные ряды – столбцы.
Две матрицы называются равными, если все элементы одной матрицы равны соответствующим элементам другой матрицы, т.е.
A = B, если 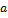 ij = bij, гдеi=
ij = bij, гдеi= 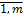 , j =
, j =  .
.
Матрица размера n × n называется квадратной.
Диагональной называется квадратная матрица, у которой все элементы, стоящие не на главной диагонали (т.е. кроме элементов с одинаковыми индексами), равны нулю.
Единичной матрицей Е называется диагональная матрица, у которой каждый элемент главной диагонали равен единице.
Пример 1.
Е3×3 = 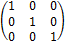
— единичная матрица 3-го порядка.
Матрица, все элементы которой равны нулю, называется нулевой. Она обозначается буквой О и имеет вид
О = 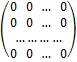 .
.
В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно).
Их вид:
А = 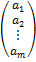 , B=
, B=  .
.
Квадратная матрица называется симметрической, если 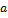 ik =
ik = 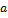 ki, т.е. равны её элементы, симметричные относительно главной диагонали. Например, симметричными являются матрицы
ki, т.е. равны её элементы, симметричные относительно главной диагонали. Например, симметричными являются матрицы
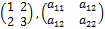 ,
, 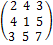 ,
, 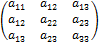 .
.
Треугольной матрицей называется квадратная матрица, все элементы которой, расположенные по одну сторону от главной диагонали, равны нулю. Различают соответственно верхнюю и нижнюю треугольные матрицы:
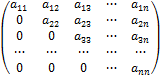
, 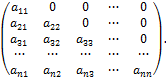
Матрица произвольных размеров
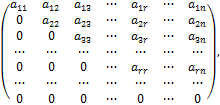
где 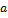 ii≠ 0 (i = 1, 2, …, r), называется квазитреугольной (ступенчатой или трапециевидной).
ii≠ 0 (i = 1, 2, …, r), называется квазитреугольной (ступенчатой или трапециевидной).
Матрицей, транспонированной к матрице А, называется матрица АТ, полученная из А заменой каждой её строки столбцом с тем же номером.
Пример 2.
А = 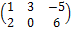 ;
; 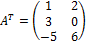 .
.
Транспонированная матрица обладает следующим свойством:
(АТ)Т = А.
Дата: 2019-12-10, просмотров: 413.