Пусть двухполюсник содержит один или несколько резистивных, индуктивных и емкостных элементов. Под резонансным режимом работы двухполюсника понимают режим, при котором входное сопротивление двухполюсника является чисто активным. По отношению к внешней цепи двухполюсник в резонансном режиме ведет себя как резистивный элемент с активным сопротивлением, поэтому ток и напряжение на входе двухполюсника совпадают по фазе. При этом реактивная мощность двухполюсника равна нулю.

Различают две основные разновидности резонансных режимов: резонанс напряжений и резонанс токов.

Резонанс напряжений

Резонанс напряжений возможен в неразветвленном участке цепи, схема замещения которого содержит индуктивный L, емкостной C и резистивный R элементы (рис. 2.11,а). На схеме пунктирной линией обозначен двухполюсник с входными зажимами а и в.

При резонансе ток в цепи İ должен совпадать по фазе с напряжением на входе двухполюсника 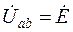. Это возможно, если входное сопротивление двухполюсника

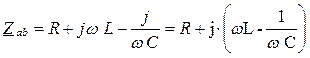
будет чисто активным, равным сопротивлению R резистивного элемента. Условие наступления резонанса напряжений в схеме рис. 2.11,а определяется равенством:

,

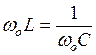из которого можно выразить резонансную угловую частоту .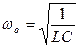

При резонансе , т.к. имеет место равенство действующих значений напряжений на индуктивном и емкостном элементах

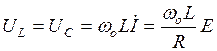
при противоположных фазах, что видно из векторной диаграммы рис. 2.11,б, на которой начальная фаза тока İ выбрана равной нулю.

Отношение

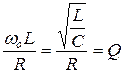
называется добротностью резонансного контура. Она показывает, во сколько раз напряжение на индуктивном (или на емкостном) элементе превышает напряжение на входе схемы в резонансном режиме. Добротность может доходить до 300 и даже больше. В большинстве случаев резонанс напряжений в электротехнических устройствах явление нежелательное, т. к. из-за больших напряжений на индуктивном и емкостном элементах может привести к повреждению изоляции.

Резонанс токов

Резонанс в цепи, состоящей из параллельно соединенных катушки индуктивности и конденсатора, называется резонансом токов. На рис. 2.12,а представлена схема замещения такой цепи, где пунктирной линией обозначен двухполюсник.

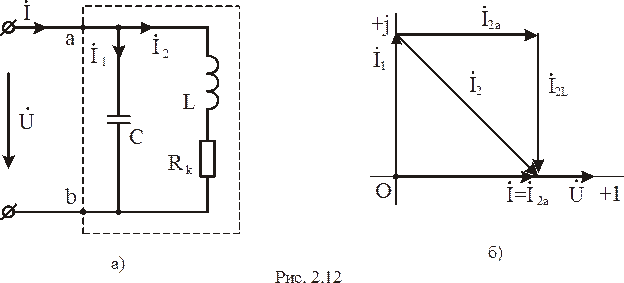
Конденсатор замещен емкостным элементом С. Катушка индуктивности является реальной и замещена индуктивным элементом L и последовательно включенным с ним резистивным элементом с активным сопротивлением R_K, учитывающим нагрев обмотки катушки. На входные зажимы двухполюсника а и в приложено синусоидальное напряжение, комплексное действующее значение которого 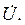 На схеме рис. 2.12,а проставлены токи с указанием положительных направлений: İ – ток в неразветвленной части схемы; İ₁  - ток первой ветви, которая имеет емкостное сопротивление 1/ωС; İ₂ – ток второй ветви, которая имеет активно – индуктивное сопротивление (R_K + ω L).

Ток İ₁ первой ветви имеет емкостной характер, опережает напряжение  на угол 90˚ и может быть записан так:

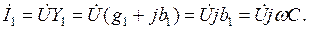
Комплексная проводимость первой ветви 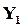имеет только мнимую часть 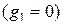:  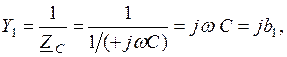где 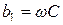 – реактивная проводимость первой ветви.

Ток 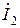 второй ветви имеет активно-индуктивный характер, отстает от напряжения  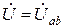и может быть записан:

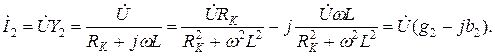
Комплексная проводимость второй ветви 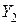имеет активную проводимость g₂ и реактивную проводимость b₂:

Ток İ в неразветвленной части схемы запишется:

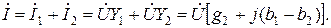      (2.11)

По определению резонансного режима, ток 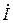 должен совпадать по фазе с входным напряжением 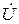двухполюсника. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю: b₁ - b₂ = 0. Следовательно, условие наступления режима резонанса токов в схеме рис. 2.12,а можно записать так:

                                                    (2.12)

На рис. 2.12,б изображена векторная диаграмма для резонанса токов. Если напряжение 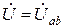отложить по действительной оси +1, то ток İ₁, имеющий емкостной характер, будет опережать это напряжение на угол 90˚. Ток İ₂ разложен на две составляющие: активную İ_2а и индуктивную İ_{2 L}. Тогда из уравнения (2.11)следует, что при резонансе токов 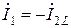, а 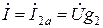, т.е. ток İ и напряжение  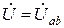на входе двухполюсника совпадают по фазе.

Резонансная частота ω₀ может быть определена из уравнения (2.12):

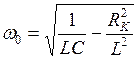
В случае представления катушки одной индуктивностью (без сопротивления R_K ) условием наступления режима резонанса токов в схеме рис.2.12,а будет:

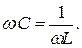                                              (2.13)

Уравнение (2.13) получено из уравнения (2.12), в котором R_K = 0. Резонансная частота ω₀ в этом случае будет определяться по формуле: 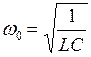. Эта формула идентична формуле резонансной частоты при резонансе напряжений.

Резонанс токов в отличии от резонанса напряжений – явление безопасное для электрооборудования.

Резонансные режимы достигаются изменением ω, L, С и R.