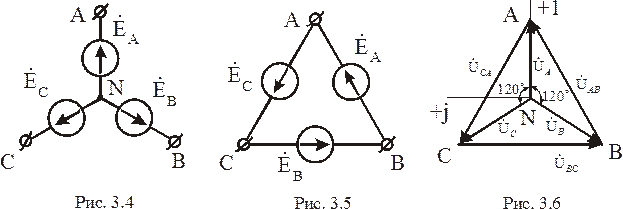
На электрической схеме трехфазный генератор, вырабатывающий трехфазную симметричную систему ЭДС (рис.3.1), изображают в виде звезды (рис. 3.4)(условное обозначение Y) или в виде треугольника (рис. 3.5)(условное обозначение Δ).
Каждую из трех фазных обмоток генератора, в которых индуцируются ЭДС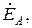 
и 
, называют соответственно фазой A, B и C.
При соединении фаз генератора звездой (рис. 3.4) концы всех трех фазных обмоток генератора объединяют в общую точку N, называемую нулевой точкой генератора. Буквы A, B и C проставляют у начала каждой из трех фазных обмоток. Таким образом, все фазные ЭДС 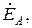и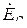 
направлены от точки N соответственно к точкам A, B и C и описываются во временной области системой уравнений (3.1), а в комплексной форме записи – системой уравнений (3.2).
При соединении фаз генератора треугольником (рис. 3.5) все фазные обмотки генератора соединяются последовательно. Например, в точку A соединены начало обмотки фазы A и конец обмотки фазы C и т. д. Все фазные ЭДС 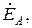и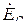 
описываются теми же уравнениями (3.1) и (3.2). Геометрическая сумма ЭДС в замкнутом треугольнике равна нулю. Поэтому если к зажимам A, B и C не присоединены приемнмки, то по фазам генератора не будет протекать ток.
Следует иметь в виду, что расположение ЭДС на комплексной плоскости не следует связывать с расположением в пространстве осей трех обмоток генератора.
Если фазы трехфазного генератора соединить с помощью линейных проводов с тремя приемниками энергии, то по проводам потекут токи, которые называются линейными. Три приемника энергии (три фазы приемника) могут быть соединены либо звездой (имеет общую точку n) либо треугольником. Возможны 5 вариантов конструктивного выполнения трехфазной цепи: “звезда – звезда с нулевым проводом”, “звезда – звезда без нулевого провода”, “звезда - треугольник”, “треугольник - звезда” и “треугольник - треугольник”.
Рассмотрим трехфазную цепь, выполненную по схеме рис. 3.7 “звезда – звезда с нулевым проводом”. Схема изображена для расчета комплексным методом.
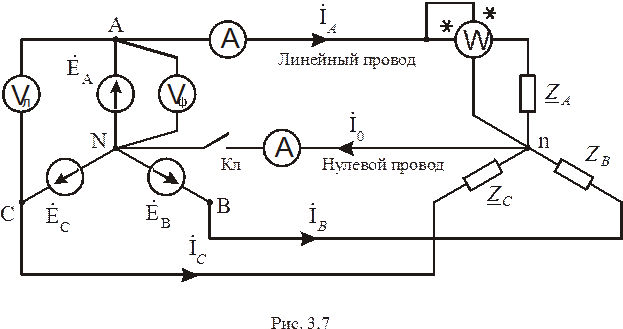
Трехфазная цепь имеет четыре провода (Кл - замкнут). Токи, протекающие по линейным проводам, называют линейными, их обозначают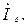 
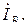
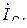Нулевым (нейтральным) называют провод, соединяющий общие (нулевые) точки генератора и приемника. Положительное направление тока в нулевом проводе 
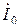берется от точки n к точке N. Для измерения модулей токов 
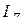в проводах используются амперметры, например электромагнитной или электродинамической систем. Напряжения на зажимах фазных ЭДС называются фазными, их обозначают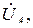 
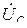(рис. 3.6). Напряжения между любыми двумя линейными проводами называются линейными и обозначаются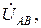 
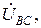
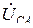(рис. 3.6). Для измерения модулей фазных 
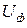и модулей линейных 
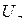напряжений применяются вольтметры, например электромагнитной или электродинамической систем. Подключение амперметров и вольтметров показано на схеме рис. 3.7.
Приемник имеет в фазе A комплексное сопротивление 
, в фазе B -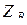 
, а в фазе С - 
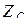. Токи, протекающие по фазам приемника, называются фазными, а напряжения на них – фазными напряжениями. Приемник называется симметричным, если одинаковы сопротивления всех трех фаз: 
. Если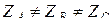 
, то приемник называется несимметричным.
При соединении фаз генератора в звезду (рис. 3.4) любое линейное напряжение по модулю в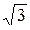 
раза больше фазного напряжения генератора. Это следует из рассмотрения равнобедренного треугольника ANB в векторной диаграмме рис. 3.6. Острые углы треугольника равны 30˚, а его основанием является линейное напряжение 
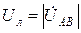. Фазные напряжения равны по модулю 
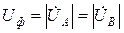. Поэтому можно записать:
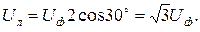
Из анализа векторной диаграммы (рис. 3.6) видно, что линейные напряжения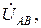 
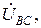
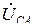опережают соответствующие фазные напряжения 
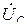на угол 30˚ и больше их по модулю в 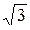раза. Поэтому имеем:
(3.3)
где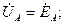 
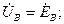
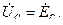
Так как трехфазные цепи являются разновидностью цепей синусоидального тока, то расчет и исследование процессов в них производятся теми же методами и приемами, которые рассматривались в гл. 2.
Расчет трехфазных цепей
В симметричном режиме работы трехфазной цепи с одной стороны имеют симметричный трехфазный генератор, а с другой стороны – симметричный приемник энергии.
Рассчитаем трехфазную цепь по схеме рис. 3.7 в симметричном режиме работы. Схема имеет два узла. При наличии нулевого провода разность потенциалов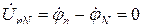 
. При этом в схеме образуются три независимые фазные цепи, каждая из которых содержит с одной стороны фазную ЭДС, например 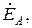а с другой стороны фазный приемник, например , соединенные между собой с одной стороны линейным проводом с током 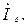а с другой – нулевым проводом с током 
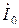. Линейные токи равны фазным токам приемника и определяются по формулам:
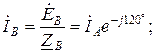
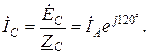
Из анализа формул видно, что все токи равны по модулю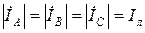 
и сдвинуты по фазе на угол 120˚. Амперметры, установленные в линейные провода, покажут одинаковые значения.
При установке в фазы симметричного приемника резистивных элементов с активным сопротивлением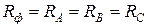 
(резистивная нагрузка) векторная диаграмма цепи представлена на рис. 3.8. Она подчеркивает тот факт, что на резистивных элементах фазные ток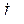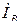и 
и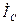 
равны по величине и совпадают по фазе с соответствующими фазными ЭДС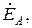 и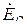 
.
Если нагрузка в фазах симметричного приемника резистивно-индуктивная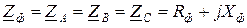 
, где 
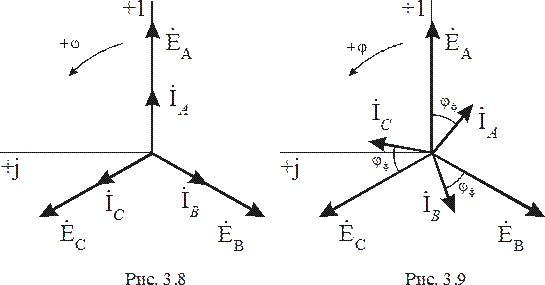
- соответственно активное и индуктивное сопротивления, то ей соответствует векторная диаграмма цепи, представленная на рис. 3.9. Из неё видно, что все фазные токи равны по величине и отстают от соответствующих фазных ЭДС на угол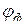 
, который рассчитывается по формуле: 
|
|
По первому закону Кирхгофа, ток в нулевом проводе 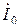равен геометрической сумме фазных токов:
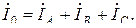
Так как режим работы симметричный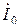 
= 0, что зафиксирует амперметр, включенный в нулевой провод. В этом случае нулевой провод может быть отключен (изъят) без изменения режима работы схемы.
При смешанной нагрузке, например, резистивно-индуктивной, в трехфазной цепи имеют место три вида мощностей.
Активная мощность трехфазной цепи запишется:
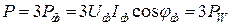, Вт, (3.4)
где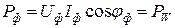 
- активная мощность одной фазы, например, А;
- фазное напряжение;
- фазный ток;
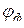– угол сдвига между фазными напряжением и током, который также можно определить из параметров нагрузки:
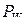– показание ваттметра, установленного как это показано на рис. 3.7, на фазные напряжение и ток фазы А приемника.
Вследствие чего, для измерения активной мощности в симметричном режиме работы трехфазной цепи достаточно установки одного ваттметра и утроения его показаний. Аналогично запишется реактивная мощность трехфазной цепи:
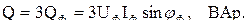(3.5)
Полная мощность цепи:
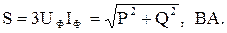(3.6)
Распишем выражение
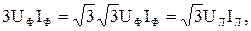
где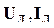 
- соответственно линейное напряжение на фазе приемника и линейный ток, протекающий по этой фазе.
Поэтому можно мощности трехфазной цепи выразить через линейные напряжения и ток:
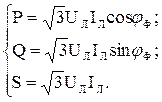
Таким образом, при симметричном режиме работы трехфазной цепи задача сводится к расчету одной из фаз, например А, аналогично расчету однофазной цепи.
Несимметричный режим работы трехфазной цепи может быть вызван: несимметричным приемником, несимметричным коротким замыканием, например, между двумя фазами, обрывом фазы и т.д.
Рассчитаем трехфазную цепь по схеме рис. 3.7 в несимметричном режиме работы, вызванном несимметричным приемником: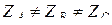 
.
Расчет трехфазной цепи существенно зависит от наличия или отсутствия нулевого провода.
При наличии нулевого провода в схеме рис. 3.7 трехфазная цепь является четырехпроводной. Разность потенциалов между узловыми точками 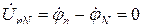. Поэтому линейные токи рассчитываются по формулам:
|
|
|
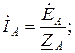
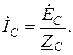
Ток в нулевом проводе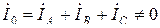 
и будет измерен амперметром, включенным в этот провод. Здесь амперметр играет роль индикатора несимметричного режима работы схемы. На рис. 3.10 приведена векторная диаграмма рассматриваемого режима. Сопротивления фаз приемника равны по величине, но имеют различный характер:
|
|
|
|
|
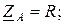
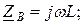
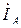по фазе совпадает с 
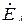, т.к. нагрузка фазы А резистивная. Ток 
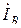на 90˚ отстает от 
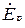, т.к. нагрузка фазы В индуктивная. Ток 
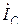опережает 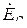на 90˚, т.к. нагрузка фазы С емкостная. Сумма токов 
Активная и реактивная мощности трехфазной цепи определяются как алгебраическая сумма мощностей фаз приемника:
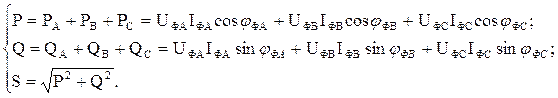(3.7)
Для измерения активной мощности трехфазной цепи необходимо иметь три ваттметра, установленные в три фазы так, как это показано на рис. 3.7 для фазы А. У всех ваттметров токовые обмотки подключаются в линейные провода фаз, а обмотки по напряжению – на зажимы фаз приемника.
В случае отключения нулевого провода в схеме рис. 3.7 трехфазная цепь становится трехпроводной. Здесь появляется разность потенциалов между узловыми точками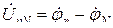 
(смещение нейтрали), которое рассчитывается по формуле:
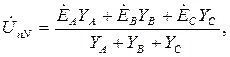
где проводимости фаз равны
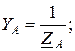
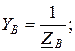
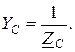
Линейные токи, равные фазным токам приемника, определяются по формулам:
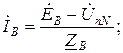
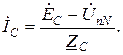
Расчет полной, активной и реактивной мощностей осуществляется соответственно по формулам (3.9), (3.10), (3.11).
Дата: 2019-12-10, просмотров: 291.
