Составим схему замещения рис. 2.4 электрической цепи рис. 2.1 для расчета тока в ней комплексным методом.

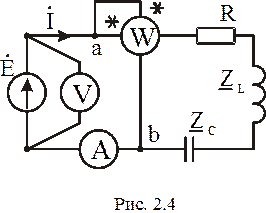Направления синусоидальных величин (ЭДС, ток и др.) в цепи периодически меняются, но одно из двух направлений принимается положительным. Это направление выбирается произвольно и указывается стрелкой на схеме. Взаимно однозначному представлению синусоидальных ЭДС, токов и других величин в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления. В схеме рис. 2.2,а мгновенное значение тока i и соответствующее ему комплексное значение İ в схеме рис. 2.4 имеют одинаковое положительное направление, указанное стрелкой и совпадающее с направлением ЭДС. Возьмем уравнение (2.2)  и перепишем его в комплексной форме:

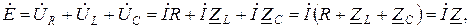           (2.6)

где 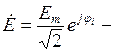комплекс действующего значения ЭДС;

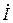 – искомый комплекс действующего значения тока;

R – сопротивление резистивного элемента;

комплексное сопротивление индуктивного элемента, где X_L= ωL – индуктивное сопротивление;

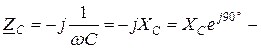комплексное сопротивление емкостного элемента, где X_С=1/ωС – емкостное сопротивление;

комплексное полное сопротивление цепи.

Запишем комплексное полное сопротивление цепи 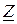в виде:

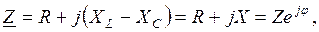       (2.7)

где 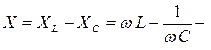реактивное сопротивление цепи;

полное сопротивление цепи;

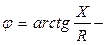аргумент полного сопротивления;

φ>0, если X_L>X_C и φ<0, если X_L<X_C.

Величина, обратная комплексному сопротивлению, называется комплексной проводимостью: Y =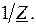

В формуле комплексного полного сопротивления цепи (2.7) R получило название активного сопротивления цепи, которое в нашем случае, т.е. в схеме рис. 2.4, равно сопротивлению резистивного элемента. Поэтому вполне обосновано употребление термина резистивный элемент с активным сопротивлением.

В цепях синусоидального тока, в активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды энергии, например в тепловую, а в реактивном сопротивлении необратимых преобразований нет.

Введение здесь понятий об активном и реактивном сопротивлениях неразветвленной цепи применяются и для характеристики более сложных цепей. В общем случае можно говорить об активном и реактивном сопротивлениях любой пассивной цепи, имеющей два вывода, т.е. пассивного двухполюсника.

Единицей всех сопротивлений; индуктивного, емкостного, активного, реактивного и полного в системе СИ является ом (Ом), а единицей проводимости – сименс (См).

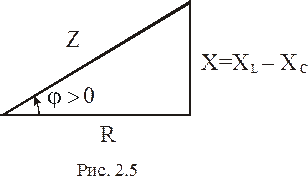Все три сопротивления цепи: активное R, реактивное X и полное Z образуют прямоугольный треугольник сопротивлений (рис. 2.5).

В треугольнике полное сопротивление Z является гипотенузой, а активное R и реактивное X являются катетами. Все три сопротивления связаны                                                          формулой: .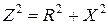

Из уравнения (2.6) искомый ток İ цепи запишется как

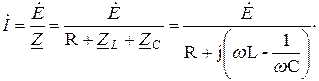                               (2.8)

Уравнение (2.8) описывает закон Ома в комплексной форме: комплексный ток в цепи (или в участке цепи) прямопропорционален комплексной ЭДС цепи (или ее участка) и обратнопропорционален комплексному полному сопротивлению цепи (или ее участка).