Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1

Пусть необходимо определить ток İ₁, протекающий через индуктивное сопротивление jX_{L 1} схемы рис. 2.13. По отношению к выделенному сопротивлению вся оставшаяся схема заключается в активный двухполюсник (АД) (рис. 2.14), содержащий эквивалентный генератор, ЭДС которого равна напряжению холостого хода на зажимах выделенного сопротивления 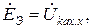 а внутреннее сопротивление равно входному сопротивлению  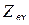активного двухполюсника. Из рис. 2.14 видно, что искомый ток İ₁ можно определить по закону Ома:

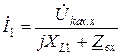.                                        (2.19)

При определении входного сопротивления  всей схемы по отношению к зажимам ka (рис. 2.14) (то же самое  АД) необходимо в схеме рис. 2.13 источники питания заменить их внутренними сопротивлениями.

 

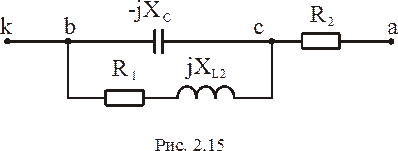
Итак, согласно рис. 2.15 входное сопротивление  запишется:

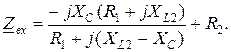                            (2.20)

Напряжение холостого хода 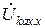 может быть определено как разность потенциалов на зажимах ka при размыкании этого участка в схеме рис. 2.13. Схема для расчета  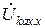представлена на рис. 2.16.

Применим формулу (1.4) падения напряжения для участка цепи, содержащего ЭДС, при определении 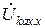 в схеме рис. 2.16:

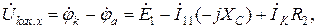                                  (2.21)

где контурный ток İ₁₁ определяется из уравнения:

                           

 

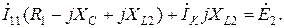
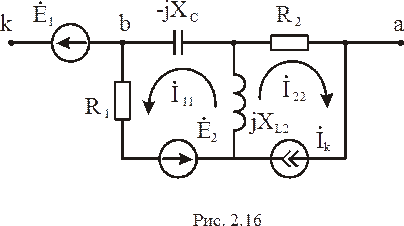
После подстановки выражений входного сопротивления 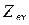 (2.20) и напряжения холостого хода  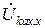(2.21) в уравнение (2.19) определяется искомый ток İ₁.

Напряжение холостого хода 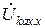 может быть определено через ток короткого замыкания  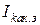между зажимами ka и входное сопротивление :

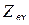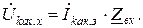
В режиме короткого замыкания зажимы ka в схеме рис. 2.13 замыкаются проводником. В этом случае 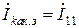, а контурный ток  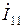находится из системы уравнений:

 

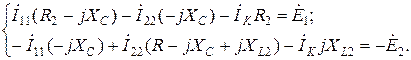
Метод двух узлов

Когда схема имеет всего два узла (рис. 2.17), наиболее рациональным методом расчета токов в ней является метод двух узлов.

 

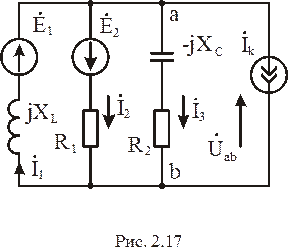
Межузловое напряжение 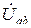определяется по формуле:

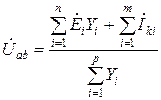                          ,                             (2.22)

где 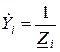– комплексная проводимость i–той ветви;

n – число ветвей с источниками ЭДС;

m – число ветвей с источниками тока;

p – число ветвей с сопротивлениями.

Для схемы рис. 2.17 имеем:

 

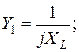
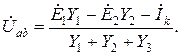
Так как у идеального источника тока внутреннее сопротивление равно бесконечности, то проводимость ветви, в которой он установлен, равна нулю.

Источник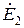и  и 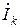  направлены от узловой точки a, которая в индексе падения напряжения 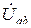стоит первой, поэтому в алгебраические суммы числителя уравнения (2.22) они входят со знаком минус.

После определения межузлового напряжения 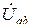находят токи в ветвях. Токи İ₁ и İ₂ определяются соответственно по формулам (1.5) и (1.2) падения напряжения для участка цепи, содержащего ЭДС:

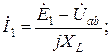
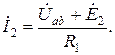
Ток İ₃ определяется по формуле (1.2) падения напряжения для участка цепи, не содержащего ЭДС (E = 0):

Проверка правильности решения осуществляется по первому закону Кирхгофа: