Рассмотрим подключение приемника, фазы которого соединены в треугольник, к трехфазной линии, входные клеммы которой обозначены на схеме рис. 3.11 буквами А, В и С. Питание трехфазной линии осуществляется от трехфазного генератора с симметричной трехфазной системой ЭДС.

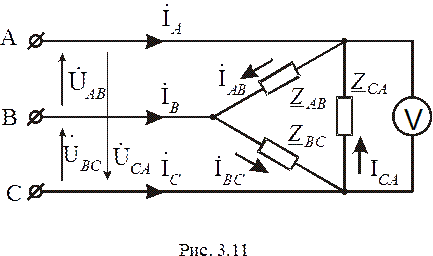
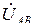Выберем положительные направления токов в фазах приемника (на сторонах треугольника) в соответствии с рис. 3.11. Ток  вызывается линейным напряжением . Величина и фаза его по отношению к напряжению 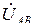определяются сопротивлением фазы приемника 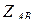. Ток 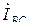 создан напряжением 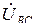. Величина и фаза его по отношению к  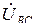определяются сопротивлением 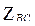. Ток 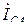 вызван напряжением  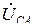и определяется сопротивлением .

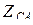В схеме рис. 3.11 линейные напряжения 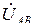,  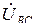и 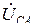 одновременно являются фазными напряжениями приемника. Поэтому вольтметр, подключенный на любую фазу приемника, покажет равенство модулей линейного и фазного напряжений .

Токи в линейных проводах определяются как в симметричном так и в несимметричном режимах работы цепи по первому закону Кирхгофа через фазные ток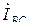и ,  и :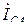

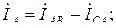
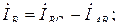
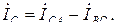
Фазные токи, протекающие по сторонам треугольника, рассчитываются по закону Ома:

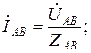
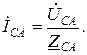                                      (3.8)

Если фазы генератора, подключаемого к клеммам А, В и С (рис. 3.11), соединены звездой (рис. 3.4), то линейные напряжения 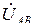,  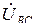и 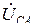 определяются по формулам (3.3).

Если фазы генератора, подключаемого к клеммам А, В и С (рис.3.11), соединены треугольником (рис .3.5), то линейные напряжения запишутся:

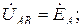
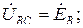
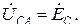
При симметричном приемнике 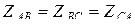 фазные токи (3.8) образуют на векторной диаграмме симметричную звезду векторов, сдвинутых по фазе на 120˚, а по модулю  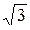раза меньше линейных токов. Векторная диаграмма токов при резистивной нагрузке для этого случая показана на рис. 3.12. Фазные ток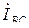и ,  и 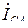 совпадают по фазе (направлению) с линейными напряжениям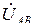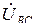и ,  и .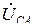

При несимметричном приемнике линейные токи могут быть и больше и меньше фазных токов приемника.

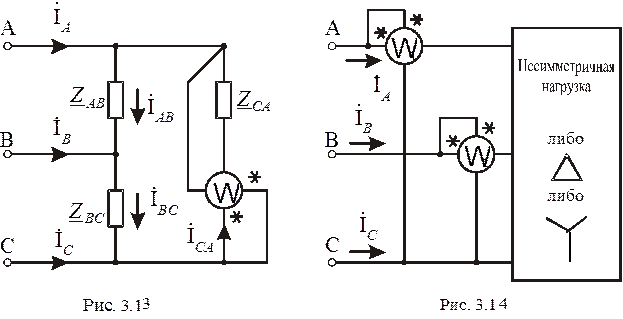
Определение мощности трехфазной цепи при соединении фаз приемника в треугольник зависит от симметрии последнего. Если приемник симметричный, то активная мощность Р трехфазной цепи определяется по формуле (3.4), реактивная мощность Q – по формуле (3.5), а полная мощность S – по формуле (3.6). Для измерения активной мощности цепи достаточно установки одного ваттметра в фазу приемника, как это показано на рис. 3.13, и утроения его показаний:

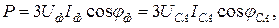
где 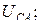 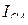– модули фазных напряжения  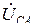и тока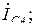

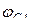 – угол между фазными напряжением 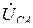и током .

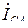Если приемник несимметричный, т.е. 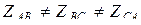, то определение полной мощности S̃ трехфазной цепи осуществляется, например по формуле:

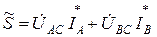                ,                                                 (3.9)

где 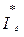,  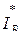- сопряженные комплексы линейных токов соответственно фазы А и фазы В.

Активная мощность трехфазной цепи может быть измерена двумя ваттметрами W ₁ и W ₂, как это показано на рис. 3.14. Первый ваттметр W ₁ установлен на линейные ток  и напряжение 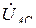, а второй ваттметр W ₂ – на ток  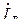и напряжение 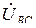. Активная мощность цепи, как сумма показаний двух ваттметров, может быть представлена действительной частью Re от полной мощности S̃:

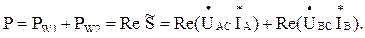                                     (3.10)

Реактивная мощность цепи может быть выражена как мнимая часть Im от полной мощности S̃:

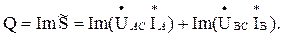                                              (3.11)

Следует отметить, что формулы (3.9), (3.10) и (3.11) справедливы при несимметричной нагрузке, фазы которой соединены либо треугольником (∆) либо звездой ( ) (рис. 3.14).