Для схемы рис. 2.2,а запишем уравнение по второму закону Кирхгофа: алгебраическая сумма ЭДС замкнутой цепи равна сумме напряжений на её участках:

                     (2.2)

где  напряжение на резистивном элементе, имеющем сопротивлением R;

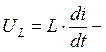напряжение на индуктивном элементе, имеющем индуктивность L;

напряжение на емкостном элементе, электрическая ёмкость которого С.

Уравнение (2.2) составлено для мгновенных значений и является интегро-дифференциальным. Решение его относительно тока осуществляется символическим (комплексным) методом. Суть метода состоит в том, что при синусоидальном токе можно перейти от интегро-дифференциальных уравнений к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС. Этот переход основан на представлении синусоидально изменяющейся величины(ЭДС, тока, напряжения) комплексным числом. Например, если мгновенное значение тока записано как

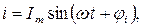                               (2.3)

то комплексная амплитуда тока 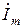будет иметь вид:

Точка наверху комплексной амплитуды İ _m обозначает изображение тока в комплексном виде. Максимальное значение тока I_m и его начальная фаза j_i, входящая в аргумент (wt + j_i) показательной функции, берутся из мгновенной формы записи тока (2.3). Вектор 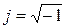, входящий также в аргумент показательной функции, указывает на комплексное число.

Комплексные числа – это вектора. С целью единообразия изображения комплексных чисел на комплексной плоскости (рис. 2.3) принимается wt=0. Тогда выражение (2.3) для комплексной амплитуды тока примет вид:

                           (2.4)

Например:

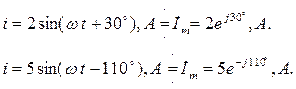
Любое комплексное число 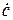 (2.5) можно записать в показательной, тригонометрической и алгебраической формах:

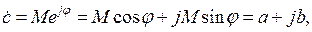                   (2.5)

где комплексная амплитуда (модуль) числа;

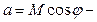действительная часть комплексного числа;

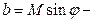коэффициент мнимой части комплексного числа;

φ – начальная фаза (угол) комплексного числа.

Комплексное число 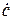, как показано на рис. 2.3, может находиться в любой из четырех четвертей комплексной плоскости. При переводе  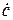из алгебраической формы в показательную, модуль М комплексного числа определяется одинаково для всех четвертей комплексной плоскости: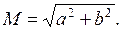

II ч .                                                                                                  I ч .

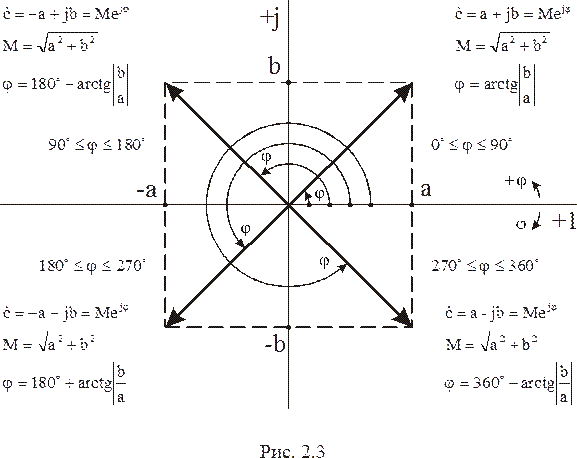
III ч .                                                                                                IV ч .

Начальная фаза (угол) φ комплексного числа может быть отсчитана, как это показано на рис. 2.3, от действительной оси +1 против часовой стрелки, если она положительна (+φ), или по часовой стрелке, если она отрицательна (-φ). Для всех четырех четвертей комплексной плоскости (рис. 2.3) приведен расчет положительной начальной фазы (+φ). Аналогичные расчеты можно провести для отрицательной начальной фазы (-φ).

Для расчета цепей синусоидального тока комплексным методом наиболее часто используют комплексное действующее значение величины (ЭДС, тока, напряжения), которое в 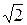 раз меньше комплексной амплитуды. Так, комплекс действующего значения тока İ запишется:

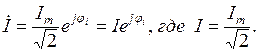
Например:

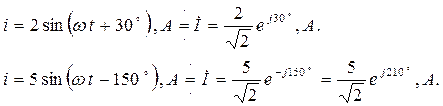
Следует отметить, что в представленном выше примере начальная фаза (угол) φ = -150˚ в комплексе действующего значения тока İ отсчитывается от действительной оси +1 по часовой стрелке, а угол φ = 360˚-150˚=210˚ отсчитывается от той же оси +1, но против часовой стрелки (рис. 2.3). Любая форма записи угла в токе İ верна.

С комплексными числами производят различные арифметические действия. В виде комплексных чисел записывают токи, напряжения, сопротивления, мощности и т.д.

Складывают и вычитают комплексные числа в алгебраической форме. Например, требуется сложить и вычесть два числа Ċ₁ = 4 + j3 и Ċ₂ = 5 - j5. Сумма Ċ₃ и разность Ċ₄ запишутся:

Ċ₃ = Ċ₁ + Ċ₂ = 4 + j3 + 5 – j5 = 9 – j2;

Ċ₄ = Ċ₁ – Ċ₂ = 4 + j3 – (5 – j5) = -1 + j8.

Как видно из записи чисел Ċ₃ и Ċ₄ действительные и мнимые их части получены алгебраическим сложением действительных и мнимых частей чисел Ċ₁ и Ċ₂ .

Умножают и делят комплексные числа в показательной форме записи. Например, требуется перемножить и разделить два числа Ċ₅ = 24е ^j120˚ и Ċ₆ = 6е ^-j40˚. Произведение этих чисел Ċ₇ запишется:

 Ċ₇ = Ċ₅ · Ċ₆ = 24е ^j120˚ · 6е ^{–j 40˚} = 144е ^{j 80˚} .

Здесь перемножаются модули комплексных чисел 24·6 = 144 и складываются их аргументы j120˚- j40˚ = j80˚.

Частное Ċ₈ от деления числа Ċ₅ на число Ċ₆ запишется как

Здесь модуль частного получен при делении модулей делимого и делителя 4 = 24/6, а аргумент частного – как разность аргументов делимого и делителя j160˚ = j120˚ - (-j40˚).

Следует отметить, что преобразование комплексного числа из алгебраической формы записи в показательную и наоборот осуществляется по формуле (2.5).

Рассмотрим умножение комплексного числа Ċ на j и на – j. В показательной форме записи Ċ = М е ^{j φ}, j = е ^j90˚, – j = е ^{–j 90˚}. Проведем умножение j·Ċ = М е ^{j φ} · е ^j90˚ = М е ^{j (φ + 90˚)}, которое не изменило модуль М числа Ċ, но на 90˚увеличило его аргумент. Если число Ċ изобразить вектором на комплексной плоскости, то умножение Ċ на j поворачивает Ċ на угол 90˚ против часовой стрелки (в сторону опережения) без изменения модуля М.

Теперь проведем умножение –j·Ċ = М е ^{j φ} · е ^{–j 90˚} = М е ^{j (φ - 90˚)}, из которого видно, что модуль М комплексного числа Ċ не изменился, а его аргумент уменьшился на 90˚. Это приведет к повороту вектора Ċ на комплексной плоскости на угол 90˚ по часовой стрелке (в сторону отставания) без изменения модуля М.

Укажем, что символический метод расчета цепей позволяет применять для синусоидальных токов все методы расчета, известные из теории цепей постоянного тока.