Нетрудно видеть, что в рамках общей МВР возможны различные варианты полноты /определенности/ информации о состоянии объективных условий. Это обстоятельство, а также качественный характер результатов, оказывают влияние на выбор критерия принятия решений. Обычно выделяют три ситуации принятия решений: принятие решений в условиях полной определенности, в условиях рынка и условиях неопределенности.
 1. Принятие решений в условиях определенности. Возможно только одно состояние объективных условий
1. Принятие решений в условиях определенности. Возможно только одно состояние объективных условий  . Ему соответствует прогноз
. Ему соответствует прогноз  =1. Тогда говорят, что решение принимается в условиях достоверности /условиях полной определенности/. Оптимальной является стратегия Siопт, на которой достигается
=1. Тогда говорят, что решение принимается в условиях достоверности /условиях полной определенности/. Оптимальной является стратегия Siопт, на которой достигается 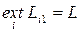 I опт 1 . При этом критерий принятия решений имеет вид
I опт 1 . При этом критерий принятия решений имеет вид 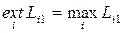 если результат желательно увеличить /например, Li1 - прибыль, объем выпуска, качество продукции и т.п./ и
если результат желательно увеличить /например, Li1 - прибыль, объем выпуска, качество продукции и т.п./ и 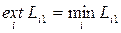 , если результат желательно уменьшить /например, Li1 – затраты, брак, время обработки и т.п./.
, если результат желательно уменьшить /например, Li1 – затраты, брак, время обработки и т.п./.
Легко показать, что любая задача линейного программирования /ЗЛП/ является частным случаем МВР данного типа. Действительно, общую модель независимо от ее конкретного содержания можно записать так:

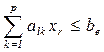
| 
|

| |

|
Тогда состояние объективных условий N1 включает:
p - число переменных;
q + p - количество ограничений;
 - матрицу коэффициентов ограничений;
- матрицу коэффициентов ограничений;
 - вектор правых частей ограничений;
- вектор правых частей ограничений;
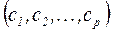 - вектор коэффициентов целевой функции.
- вектор коэффициентов целевой функции.
Множество стратегий (Si) образуют все допустимые планы задачи, т. е. значения переменных х1, х2, …, хn, удовлетворяющие ограничениям общей модели ЗАП, а количество этих планов равно n. Результатами (Li1) являются значения целевой функции Li1=  на каждом допустимом плане, а max
на каждом допустимом плане, а max  .
.
2. Принятие решений в условиях риска. Если возможны дваили более состояний объективных условий, поддающиеся точному определению, и если вероятность их возникновения или прогноз с той или иной степенью точности установлены, то налицо выбор решения в условиях риска.
В качестве критерия принятия решения в таких задачах используется критерий Байеса - Лапласа, при котором находится максимум или минимум среднего результата

Выбор максимума или минимума определяется исходя из способа оценки эффективности результата. Если такая оценка произведена через разного рода затраты то, естественно, оптимальной стратегией является стратегия, соответствующая минимуму средневзвешенных по вероятности возникновения состояний объективных условий результатов ее применения. В противном случае, при оценке результатов по положительному эффекту выбирается стратегия, соответствующая минимуму указанной средней величины.
Если прогноз P1, P2,… ,Pm определен объективно с позиций частотного подхода, то говорят, что имеет место определенность, только определенность статистическая.
Пример 1. Пусть руководитель производства рассматривает три варианта технологических процессов изготовления радиоэлектронного устройства S1, S2, S3. При этом объективные условия соответствуют либо тому факту, что в рассматриваемый период времени для изготовления устройства удается применить интегральные схемы определенных типов N1 либо не удается N2. На основе предыдущего опыта руководитель оценивает прогноз состояний N1 как P1 =3/4, а состояния N2 как P2 =1/4. Результатами Lij является суммарная прибыль от реализации изделия, изготовленного по соответствующим технологическим процессам.
Запишем условия задачи в матричной форме:
| N | N1 | N2 | Liср |
| P | 3/4 | 1/ 4 | |
| S1 | 6,5 | 9,5 | 7,3 |
| S2 | 9,0 | 7,5 | 8,6 |
| S3 | 6,0 | 11.0 | 7,2 |
Вычислим каждый результат для каждой стратегии
L1ср=  PjLij =3/4 * 6,5 + 1/4* 9,5 » 7,35
PjLij =3/4 * 6,5 + 1/4* 9,5 » 7,35
L2ср=  PjLij=3/4 * 9,0 + 1/4* 7,5 » 8,6
PjLij=3/4 * 9,0 + 1/4* 7,5 » 8,6
L3ср=  PjLij= 3/4 * 6,0 + 1/4* 11,0 » 7,2
PjLij= 3/4 * 6,0 + 1/4* 11,0 » 7,2
и найдем  L1ср = 8,6который достигается, если выбрать второй вариант технологии изготовления изделияS2.
L1ср = 8,6который достигается, если выбрать второй вариант технологии изготовления изделияS2.
3. Принятие решений в условиях неопределенности. К сожалению, прогнозирование вообще, и особенно на длительные сроки имеет весьма сомнительную ценность. Поэтому на практике часто встречаются случаи, при которых сделать сколько-нибудь достоверный прогноз невозможно, т.е. вероятность возникновения объективных условий неизвестна. Вся информация о ситуации заключена только в матрице результатов. Традиционным путем преодоления неопределенности, связанным прогнозом, является применение различных критериев выбора решения и в условиях неопределенностии, прежде всего, критериев "недостаточного основания", Вальда, Сэвиджа, Гурвича. Каждый из критериев, кроме первого, ориентирует на получение некоторого гарантированного результата.
Критерий "недостаточного основания". Этот критерий является частным случаем критерия " Байеса-Лапласа. Он используется, когда у лица, принимающего решение, нет оснований предполагать, что одни состояния объективных условий более вероятны, чем другие. Тогда естественно положить все Nj (j=  ) равновероятными, т.е. Pj =1/m (j =
) равновероятными, т.е. Pj =1/m (j =  ). Введенный таким образом прогноз позволяет свести задачу к выбору решения в условиях риска, с критерием
). Введенный таким образом прогноз позволяет свести задачу к выбору решения в условиях риска, с критерием  Lij.
Lij.
 Найдем оптимальную стратегию в рассмотренном выше примере с данным критерием. Имеем
Найдем оптимальную стратегию в рассмотренном выше примере с данным критерием. Имеем
L1ср= 1/2 * 6,5 + 1/2* 9,5 =8
L2ср= 1/2 * 9,0 + 1/2* 7,5 =8,25
L3ср= 1/2 * 6,0 + 1/2* 11,0 =8,5
Оптимальной является стратегия S3.
Критерий Вальда /минимаксный или максимальный критерий/.
В соответствии с критерием Вальда для каждой стратегии находится наихудший среди возможных результатов и выбирается такая стратегия, которая приводит к наилучшему из наихудших результатов, т.е. к минимуму из максимальных потерь, либо к максимуму из минимальных эффектов. В первом случае этот критерий имеет вид:  Lij
Lij
во втором  Lij
Lij
Рассмотрим матрицу результатов примера 1 с максиминным критерием
| N1 | N2 | Наихудшие результаты (min L ij) |
| 6,5 | 9,5 | 6,5 |
| 9,0 | 7,5 | 7,5 |
| 6,0 | 11,0 | 6,0 |
Оптимальной является стратегия S2 , на которой достигается  .
.
При использовании критерия Вальда лицо, принимающее решение, считает, что объективные условия не нейтральны, а враждебны ему.
Критерий Сэвиджа. Его называют также критерием минимаксного сожаления или принципом минимакса последствий ошибочных решений.
Согласно этому критерию, при отсутствии полной информациио состоянии объективных условий, принимающий решение должен попытатьсясвестик минимуму возможные сожаления или, каких еще называют, "потериот упущенных возможностей". Под ними подразумевается разность между издержками при любой и при оптимальной для данных объективных условий стратегий. Рассчитав таким образом сожаления для всех возможных объективных условий и стратегий, составляют матрицу сожалений или последствийошибочных решений. Далее к этой матрицаприменяют критерий Вальда.
Аналитическая форма критерия Севиджа имеет следующий вид:
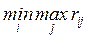
где rij – потери /сожаления/ от упущенных возможностей при выборе стратегии Si и наступлении объективных условий Nj.

| 
|

|
Здесь, как и ранее ищется максимум, если результаты Lij, желательно иметь побольше, и минимум - в противном случае.
В примере 1 
а матрица потерь (rij) имеет вид:
| N1 | N2 | Наибольшие потери (  ) )
| |
| S1 | 2,5 | 1,5 | 2,5 |
| S2 | 4,5 | 4,5 | |
| S3 |
Оптимальной является стратегия S1, на которой достигается

Критерий Гурвича. Этот критерий рекомендует при выборе стратегий рассчитывать на осуществление промежуточного между наилучшими и наихудшими состояниями объективных условий.
Формально критерий Гурвича можно записать так:
 ,
,
где a выбирается из интервала между 0 и 1. Если результаты представляют собой потери, то в последнем критерии  заменяется на
заменяется на  .
.
Коэффициент a является как бы мерой оптимизма лица, принимающего решение. Его выбор субъективен и зависит от темперамента и личной оценки ситуации индивидуумом. Если a близок к 1, то значение критерия Гурвича стремится к значению критерия Вальда. При a близком к 0 значение приближается к значению критерия "крайнего оптимизма"  . Часто a выбирается равным 1/2.
. Часто a выбирается равным 1/2.
Таким образом, при выборе решений в условиях неопределенности могут быть использованы несколько различных критериев, которые, весьма вероятно, могут привести к различным вариантам решений. Сложный, но хорошо разработанный аппарат теории игр, позволяет находить оптимальное решение и в этом случае. Вместе с тем, сам способ преодоления неопределенности с помощью игровых критериев с научно-методической точки зрения во многих ситуациях выглядит недостаточно убедительно. Без привлечения какой-либо дополнительной информации неопределенность вдруг исчезает, стоит только применить тот или иной игровой критерий. Естественно ожидать, что неопределенность может быть ликвидирована лишь привлечением дополнительной информации и ничем больше. Это должна быть внемодельная информация, которая на этапе построения модели не может быть собрана и формализована, важным источником такой информации является опыт руководителя, хорошо знакомого с ситуациями, походившими на описываемую в модели. Руководители и специалисты всегда знают о состоянии производства больше того, что нашло отражение в модели в силу неизбежной ограниченности последней и трудной формализуемости ряда сведений. Это могут быть и более или менее правдоподобные догадки о возможности развития событий и т.п.
Рассмотрим процесс принятия решений при неполной информации на условном примере.
Завод изготовляет приборы радиоэлектроники. Отдел главного конструктора выпустил извещение на изменение конструкции нескольких приборов, которое, в частности, предусматривало применение вместо устаревшего новые, более надежные блоки, только что освоенные электронной промышленностью. Оптимальная величина Z резервного запаса покупного полуфабриката может быть определена как значение, на котором достигается

где  - среднее количество отказов в обеспечении производства полуфабрикатами данного вида;
- среднее количество отказов в обеспечении производства полуфабрикатами данного вида;
h(z) - средняя длительность одного отказа;
С' - средние потери в производстве на один случай отказа длительностью в один день /удельные потеря/;
С” - годовые приведенные затраты на создание и содержание единицы резервного запаса /удельные затраты/.
Таким образом, в этой постановке стратегиями является набор различных величин резервных запасов. Как и во всякой задаче выбора решения перед нами встает проблема прогнозирования состояния объективных условии. В рассматриваемом случае неопределенность проявляется через ситуации, складывающиеся в результате отказа /задержки поставки полуфабрикатов на сборку/ - рис. 8.
 Потери для рассматриваемого случая составят: С’(N1)=20 руб., С’(N2)=40 руб. Удельные затраты для данного полуфабриката С"=50 руб. Для простоты будем считать, что администрация предприятия может принимать лишь одну из четырех следующих стратегий: установить резервный запас размером 10, 20, 30 и 40 штук. Рассчитать совокупные издержки для всех возможных сочетаний стратегий и состояний объективных условий.
Потери для рассматриваемого случая составят: С’(N1)=20 руб., С’(N2)=40 руб. Удельные затраты для данного полуфабриката С"=50 руб. Для простоты будем считать, что администрация предприятия может принимать лишь одну из четырех следующих стратегий: установить резервный запас размером 10, 20, 30 и 40 штук. Рассчитать совокупные издержки для всех возможных сочетаний стратегий и состояний объективных условий.
Рис. 8. Схема образования потерь из-за отказа в поставке полуфабрикатов
Стратегии адм.
предп. 
| 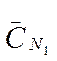
| 
| 
|
Отсюда получаем матрицу альтернативных потерь.

| 
| 
|
Из таблиц видно, что для данного примера, исходя из критерия Вальда, следует установить  = 40, из критерия Сэвиджа
= 40, из критерия Сэвиджа  =10. Пусть теперь состояние объективных условий (ситуаций)
=10. Пусть теперь состояние объективных условий (ситуаций)  возникает с вероятностью Р(
возникает с вероятностью Р(  ) , а ситуация
) , а ситуация  - с вероятностью Р(
- с вероятностью Р(  ). Понятно, что Р(
). Понятно, что Р(  )+ Р(
)+ Р(  )=1. Отложим на оси абсцисс вероятность возникновения ситуации Р(
)=1. Отложим на оси абсцисс вероятность возникновения ситуации Р(  ), а на ординате - затраты, соответствующие этой вероятности при условии применения каждой из четырех стратегий. На рисунке 9 показано, как изменяется решение по мере изменения Р(
), а на ординате - затраты, соответствующие этой вероятности при условии применения каждой из четырех стратегий. На рисунке 9 показано, как изменяется решение по мере изменения Р(  ) от 0 до 1. Жирная ломаная линия соответствует минимальным издержкам, при различных вероятностях состояний объективных условий
) от 0 до 1. Жирная ломаная линия соответствует минимальным издержкам, при различных вероятностях состояний объективных условий  и
и  .
.
Из рис. 9 видно, что при Р(  ) £ 0,4 оптимальной стратегией будет установление
) £ 0,4 оптимальной стратегией будет установление  =10, при 0,4 £ Р(
=10, при 0,4 £ Р(  ) £ 6 оптимальным будет
) £ 6 оптимальным будет  = 20,
= 20,
при 0,6 < Р(  )£ 0,835
)£ 0,835
 = 30, при Р(
= 30, при Р(  ) > 0,835
) > 0,835  =40.
=40.
Сравним эти полученные на графике результаты с результатами, найденными с помощью рассмотренных критериев. Из сравнения видно, что использование критерия Вальда практически равнозначно приписыванию вероятности состояния объективных условий значения, превышающего 0,835. Установив в соответствии с критерием Вальда резервный запас  =40, администрация предприятия тем самым предполагает (хотя и несознательно), что ситуация
=40, администрация предприятия тем самым предполагает (хотя и несознательно), что ситуация  возникает с большей вероятностью, чем ситуация
возникает с большей вероятностью, чем ситуация  . То есть, руководствуясь каждым из критериев, принимающий решение придает определенное значение вероятности состояний объективных условий уже самим актом избрания определенной стратегии.
. То есть, руководствуясь каждым из критериев, принимающий решение придает определенное значение вероятности состояний объективных условий уже самим актом избрания определенной стратегии.
Таким образом, как это видно из примера, любое решение в условиях неопределенности, отклоняющееся от принципа равновероятности состояний объективных условий, предусматривает оценку вероятностей. Хотя в данном случае вероятность нельзя ни установить, ни изменить или объяснить, тем не менее, выбирающий решение действует так, как если бы он знал о системе больше, чем он утверждает.
Нетрудно видеть, что критерий Вальда и, следовательно, критерий Сэвиджа основаны на том, что объективные условия не нейтральны, а враждебны нам. Как уже указывалось, использование данных критериев в производственных условиях требует обоснования, источником которого могут стать временные флуктуации предпочтений, не нашедшие отражения в целевой функции.
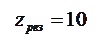

Рис. 9. Выбор  в условиях неполной информации о потерях из-за дефицита.
в условиях неполной информации о потерях из-за дефицита.
Дата: 2016-09-30, просмотров: 387.