Под содержательностью или семантикой сообщений понимается наличие понятий и суждений, характеризующих действительные и возможные состояния объектов. Известно несколько попыток, относящихся к возможности введения количественной меры семантической информации. Многие из них основываются на теории индуктивной (логической) вероятности. В частности, доказывается, что мера семантической информации 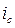должна быть функцией логической вероятности утверждения. При этом если и два высказывания и логические вероятности , то .

Бар-Хиллел и Карнап были первыми исследователями, плодотворно работавшими в области построения теории семантической меры информации. Их теория не рассматривает потребительской ценности сообщений и строится для простого языка, который содержит только повествовательные предложения (высказывания), выражающие отношения между конечным числом объектов и свойств с помощью логических связок: "не", "и", "если", "то", "если и только если". Основой теории является предложение, что данное высказывание тем более содержательно, чем меньшей определенностью оно обладает, т.е. чем большее количество описаний состояния объекта оно исключает из числа возможных, и чем больше число элементов содержания, которые логически из него не следуют. Таким образом, содержание высказывания определяется не тем, что оно содержит, а тем что исключает. Элемент содержания есть высказывание, которое обладает наименьшим содержанием и служит единицей измерения. С другой стороны, максимальным является содержание таких ложных высказываний, которые исключают все альтернативы.

В теории вводятся две связанные между собой меры содержания высказывания: вероятная мера cont ( ) и информационная мера inf ( ).

Мера cont ( ) принимает значения из промежутка [0.1], причем cont ( )=0, когда высказывание является тавтологией (например, высказывание типа "Масло масляное"), а cont ( )=1, когда - логически ложное высказывание. В остальных случаях cont ( )=1-p( ), где p( ) - логическая вероятность высказывания

и является мерой величины неожиданности высказывания .

Мера inf ( ) учитывает, что нового несет получателю сообщениепо сравнению с тем, что он зналили предполагал.

Карнап и Бар-Хиллел доказали ряд теорем, касающихся содержания высказывания. При этом оказалось, что их теория во многих отношениях обнаруживает аналогию со статистической теорией связи Шеннона. Так, теорема о содержании условных высказываний

напоминает теорему Шеннона об условной энтропии

H(X/Y) = H(X )-H(Y)

Карнап и Бар-Хиллел используют также понятие "семантического шу­ма" как причины неправильной интерпретации сообщений, которое перекликается с понятием синтактического шума как причины неправильного приема сигналов и др. Однако между этими теориями существует и принци­пиальное различие. Теория Шеннона описывает "количество информации", ограничиваясь рассмотрением знаков (сигналов) и статистических отноше­ний между ними. Это синтактическая теория, а рассматриваемые ею веро­ятности представляют собой относительные частоты знаков или их оценки (объективные вероятности). Теория Карнапа и Бар-Хиллела - семантичес­ки и как таковая включает также элементы синтактики. Бар-Хиллел утверждал, что теория Шеннона может быть полностью отображена в пред­ставлениях семантической теории, но не наоборот.

До сих пор не появилось какой-либо единой концепции прагматической информации, хотя многие теоретические и практические задачи в раз­личных областях знания, техники, экономики и управления настоятельно требуют четкого описания этого аспекта информации. Так, например, проблема оптимизации обработки массивов информации решается тем успеш­нее, чем лучше мы умеем определять и измерять ценность информации. В условиях ограниченных памяти и быстродействия компьютеров можно наилучшим обра­зом осуществлять сжатие информации и ее обработку за счет выделения и упорядочения наиболее важных и ценных с точки зрения конкретной задачии поставленной в ней цели признаков на основе установленной заранее ме­ры прагматической информации. Руководитель любого уровня для принятия решений использует непрерывно поступающие сведения о функционировании подчиненной ему системы, состоянии финансирования, материального снаб­жения и т.п. При этом он постоянно оценивает сообщения с точки зрения их полезности и выполнения функций управления.

Перспективным представляется подход к измерению ценности информа­ции в рамках байесовской теории принятия решений. Рассмотримегоособенности на условном примере.

Имеется монета и специально изготовленная игральная кость, четыре стороны которой помечены словом "герб" и остальные две словом "решетка". Наблюдать бросание монеты и кости не разрешается. Один из предме­тов накрывается чашкой.

Введем обозначения для следующих утверждений: "не накрыта монета" - ; "не накрыта кость" - ; "выпал герб" - a; "выпала решетка" - b.

Если принимающий решение правильно угадает, какой именно предмет не накрыт, он получит приз - 1 рубль. В противном случае он не получа­ет ничего. Вероятности событий и на начало эксперимента представляются равными .

Очевидно, что в этом случае ожидаемый выигрыш 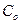= 1/2 руб. Если же точно известно, какое событие произойдет, то ожидаемый выигрыш при наличии полной и надежной информации = 1 руб.

Увеличение дохода принимающего решение по сравнению с доходом, который он получил бы на основе решений, принятых с помощью априорной информации, будем называть ожидаемой ценностью полной информации. В нашем примере 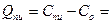1*0,5=0,5 руб.

Следовательно, максимальная сумма, которую имеет смысл заплатить за совершенно надежную информацию в нашем случае - 0,5 руб. Поскольку представляет собой прирост дохода от полного исключения неопреде­ленности, эту величину иногда называют стоимостью неопределенности.

Попробуем теперь определить ценность неполной или выборочной информации. Для этого разовьем описанный выше пример с костью и монетой.

Лицо, производящее эксперимент, сообщает принимающему решение, "гербом" или "решеткой" помечена верхняя сторона не накрытого чашкой предмета. Ясно, что такое сообщение существенно повлияет на мнение принимающего решение о том, какой предмет накрыт чашкой. Интуитивно понятно, что при выпадении "герба" то, что не накрыта кость, более вероятно. Для количественной оценки степени устранения неопределенности исполь­зуется теорема Байеса, утверждающая, что условная вероятность события А, если известно, что событие В наступило, равна

.

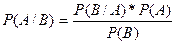Предположим, что в нашем эксперименте не накрыта монета. Тогда условная вероятность события a =1/2. Если же не накрыта кость - событие , то P(a/ )=2/3. Отсюда безусловная вероят­ность события a равна

P (a) = P(a/ )P( )+P(a/ )P( )=7/12

В соответствии с теоремой Байеса вероятность того, что не накры­та кость, если известно, что выпал "герб", определитсяиз выражения

P ( /a) = =4/7

Аналогично P =3/7

Точно таким же образом найдем условие вероятности событий и после сообщения о том, что выпала "решетка" Р( /b) = 3/5; Р( /b) = 2/5;

а Р(b)=1- P(a) =1-7/12-5/12.

Следовательно, при сообщении "герб" наилучшей догадкой является "кость", а ожидаемый доход равен 4/7 руб., при сообщении "решетка" на­илучшая догадка - "монета", а ожидаемый доход - 3/5 руб. Ожидаемый до­ход при данной выборочной информации

=7/12*4/7+5/12*3/5=7/12 руб.

Ожидаемая ценность выборочной информации в нашем случае:

=7/12-1/2=1/12 руб.

При организации системы обработки информации в управлении производством часто оказывается удобно оперироватьне количеством информации, а ее объемом, измеренным в той или иной системе единиц.