Продолжаем рассматривать неопределенность вида 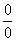
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 3
Найти предел 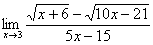

Умножим числитель и знаменатель на сопряженное выражение.
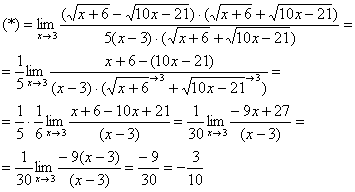
20.2 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА 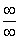
Сейчас мы рассмотрим группу пределов, когда 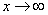 , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример 4
Вычислить предел 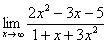
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 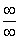 . Можно было бы подумать, что
. Можно было бы подумать, что  , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим 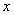 в старшей степени:
в старшей степени:
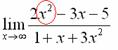
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим 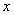 в старшей степени:
в старшей степени:
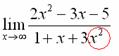
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 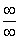 необходимо разделить числитель и знаменатель на
необходимо разделить числитель и знаменатель на 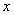 в старшей степени.
в старшей степени.
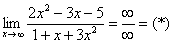
Разделим числитель и знаменатель на 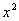
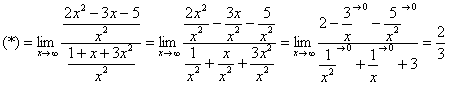
Вот оно как, ответ 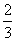 , а вовсе не бесконечность.
, а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 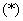 , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
, он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:
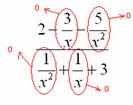
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 5
Найти предел 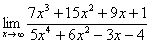
Снова в числителе и знаменателе находим 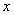 в старшей степени:
в старшей степени:
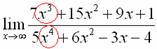
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности 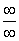 делим числитель и знаменатель на
делим числитель и знаменатель на  .
.
Полное оформление задания может выглядеть так:
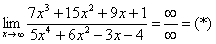
Разделим числитель и знаменатель на 
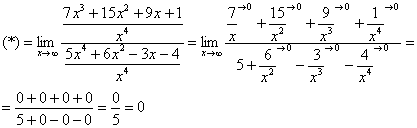
Пример 6
Найти предел 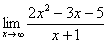
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( 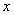 можно записать как
можно записать как 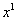 )
)
Для раскрытия неопределенности 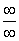 необходимо разделить числитель и знаменатель на
необходимо разделить числитель и знаменатель на 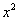 . Чистовой вариант решения может выглядеть так:
. Чистовой вариант решения может выглядеть так:
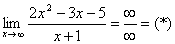
Разделим числитель и знаменатель на 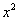
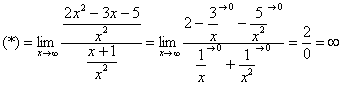
Под записью 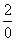 подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида 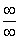 у нас может получиться конечное число, ноль или бесконечность.
у нас может получиться конечное число, ноль или бесконечность.
ПРАКТИКУМ 20
ЗАДАНИЕ N 1
Тема: Раскрытие неопределенности вида "ноль на ноль"

Решение:
Если вместо переменной  поставить значение 7, к которому она стремится, то получим неопределенность вида
поставить значение 7, к которому она стремится, то получим неопределенность вида  тогда
тогда

ЗАДАНИЕ N 2
Тема: Раскрытие неопределенности вида "ноль на ноль"

Решение:
Если вместо переменной  поставить значение 0, к которому она стремится, то получим неопределенность вида
поставить значение 0, к которому она стремится, то получим неопределенность вида  тогда
тогда
ЗАДАНИЕ N 3
Тема: Раскрытие неопределенности вида "ноль на ноль"
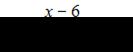
Решение:
Если вместо переменной  поставить значение 6, к которому она стремится, то получим неопределенность вида
поставить значение 6, к которому она стремится, то получим неопределенность вида  тогда
тогда

ЗАДАНИЕ N 4
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"
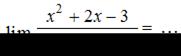
Решение:
Так как  и
и 
то имеет место неопределенность вида 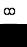
Для ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на  . Тогда, зная, что
. Тогда, зная, что 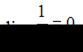 получим:
получим:

ЗАДАНИЕ N 5
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"
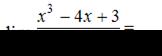
Решение:
Так как  и
и 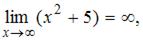
то имеет место неопределенность вида  Для ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на
Для ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на 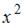 . Тогда, зная, что
. Тогда, зная, что 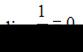 получим:
получим:
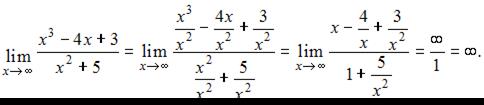
САМОСТОЯТЕЛЬНАЯ РАБОТА 20
ЗАДАНИЕ N 1
Тема: Раскрытие неопределенности вида "ноль на ноль"
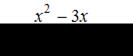
ЗАДАНИЕ N 2
Тема: Раскрытие неопределенности вида "ноль на ноль"
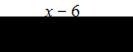
ЗАДАНИЕ N 3
Тема: Раскрытие неопределенности вида "ноль на ноль"

ЗАДАНИЕ N 4
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"
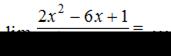
ЗАДАНИЕ N 5
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"
Предел функции  равен …
равен …
ЗАДАНИЕ N 6
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"
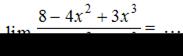
ТЕМА 21 ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ. ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
КОНСПЕКТ 21
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Рассмотрим следующий предел: 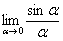 Согласно правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида
Согласно правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида 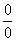 , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
, которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

Данный математический факт носит название Первого замечательного предела.
Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:
 – тот же самый первый замечательный предел.
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде 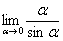 , то и решать его нужно в таком же виде, ничего не переставляя.
, то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра 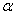 может выступать не только переменная
может выступать не только переменная 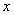 , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
, но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Примеры:
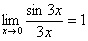 ,
, 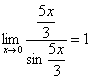 ,
,  ,
, 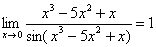
Здесь 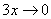 ,
,  ,
, 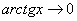 ,
, 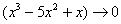 , и всё гуд – первый замечательный предел применим.
, и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
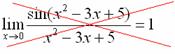
Почему? Потому-что многочлен 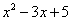 не стремится к нулю, он стремится к пятерке.
не стремится к нулю, он стремится к пятерке.
Пример 1
Найти предел 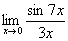
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, у нас есть неопределенность вида 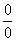 , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится
, ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится 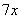 , а в знаменателе
, а в знаменателе 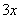 .
.
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас 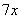 , значит, в знаменателе нам тоже нужно получить
, значит, в знаменателе нам тоже нужно получить 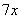 ».
».
А делается это очень просто:
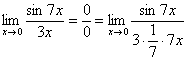
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:

Теперь только осталось избавиться от трехэтажности дроби:
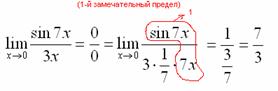
Готово. Окончательный ответ: 
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
В теории математического анализа доказано, что:
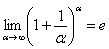
Данный факт носит название второго замечательного предела.
Справка: 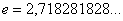 – это иррациональное число.
– это иррациональное число.
В качестве параметра 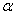 может выступать не только переменная
может выступать не только переменная 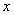 , но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.
, но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.
Пример 2
Найти предел 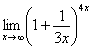
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 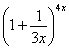
Нетрудно заметить, что при 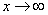 основание степени
основание степени  , а показатель –
, а показатель –  , то есть имеется, неопределенность вида
, то есть имеется, неопределенность вида 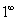 :
:
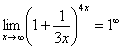
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр  , значит, в показателе нам тоже нужно организовать
, значит, в показателе нам тоже нужно организовать 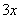 . Для этого возводим основание в степень
. Для этого возводим основание в степень 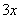 , и, чтобы выражение не изменилось – возводим в степень
, и, чтобы выражение не изменилось – возводим в степень 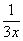 :
:
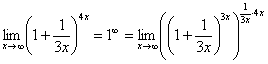
Когда задание оформляется от руки, карандашом помечаем:
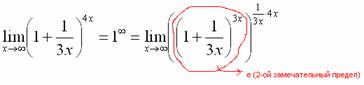
Практически всё готово, страшная степень превратилась в симпатичную букву  :
:
При этом сам значок предела перемещаем в показатель.
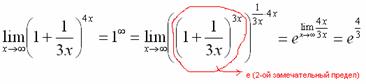
ПРАКТИКУМ 21
ЗАДАНИЕ N 1
Тема: Первый замечательный предел
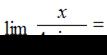 …
…
Решение:
Чтобы воспользоваться первым замечательным пределом 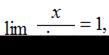
необходимо, используя соотношение  вынести множитель
вынести множитель 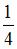 за знак предела. Тогда:
за знак предела. Тогда: 
ЗАДАНИЕ N 2
Тема: Первый замечательный предел
 …
…
Решение:
Чтобы воспользоваться первым замечательным пределом 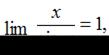
необходимо, используя соотношение  вынести множитель
вынести множитель 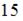 за знак предела. Тогда:
за знак предела. Тогда: 
ЗАДАНИЕ N 3
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда  равен …
равен …
Решение:
Обращаем внимание, что функцию  нужно преобразовать так, чтобы использовать второй замечательный предел – формулу
нужно преобразовать так, чтобы использовать второй замечательный предел – формулу  .
.
Для этого числитель и знаменатель дроби необходимо разделить на число  ,
,
получается 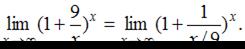
Далее нужно выполнить замену переменной, полагая 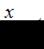 . Тогда если
. Тогда если  ,
,
то  ,
, 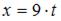 и, следовательно,
и, следовательно,
 Получаем
Получаем 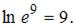
ЗАДАНИЕ N 4
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда  равен …
равен …
Решение:
Обращаем внимание, что функцию 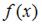 нужно преобразовать так, чтобы использовать второй замечательный предел – формулу
нужно преобразовать так, чтобы использовать второй замечательный предел – формулу  .
.
Для этого числитель и знаменатель дроби необходимо разделить на число 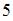 ,
,
получается 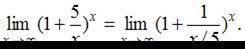
Далее нужно выполнить замену переменной, полагая 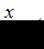 . Тогда если
. Тогда если  ,
,
то 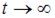 ,
, 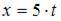 и, следовательно,
и, следовательно,
 Получаем
Получаем 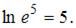
САМОСТОЯТЕЛЬНАЯ РАБОТА 21
ЗАДАНИЕ N 1
Тема: Первый замечательный предел
 …
…
ЗАДАНИЕ N 2
Тема: Первый замечательный предел
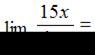 …
…
ЗАДАНИЕ N 3
Тема: Первый замечательный предел
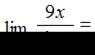 …
…
ЗАДАНИЕ N 4
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда 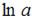 равен …
равен …
ЗАДАНИЕ N 5
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда  равен …
равен …
ЗАДАНИЕ N 6
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда  равен …
равен …
ЗАДАНИЕ N 7
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда  равен …
равен …
ЗАДАНИЕ N 8
Тема: Второй замечательный предел
Пусть  . Тогда
. Тогда  равен …
равен …
Дата: 2019-07-31, просмотров: 336.