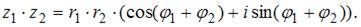
Возведение комплексных чисел в степень
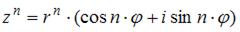формула Муавра
Пример 2
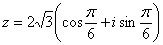найти 
.
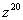Тогда, по формуле Муавра:
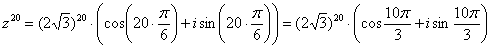
Упаси боже, не нужно считать на калькуляторе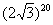 
, а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет 
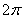радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе 
: 
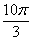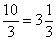оборотов, в данном случае можно убавить один оборот: 
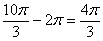. Надеюсь всем понятно, что 
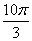и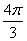 
– это один и тот же угол.
Таким образом, окончательный ответ запишется так:
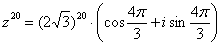
Любители стандартов везде и во всём могут переписать ответ в виде:
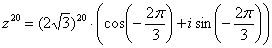(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя 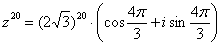– ни в коем случае не ошибка.
ПРАКТИКУМ 18
ЗАДАНИЕ N 1
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа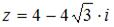 
имеет вид …
Решение:
Для представления комплексного числа в тригонометрической форме записи
необходимо найти его модуль и аргумент.
Используя формулу 
, где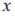 
– действительная, а 
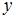– мнимая часть комплексного числа, получим:
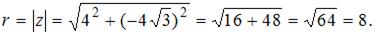
По формулам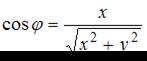 
и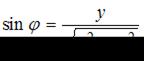 
найдем аргумент 
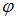комплексного числа.
Обращаем внимание, что под аргументом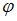 
понимается его главное значение, то есть значение, удовлетворяющее условию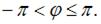 
Так как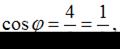 
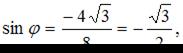то 
Зная, что тригонометрическая форма комплексного числа имеет вид
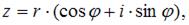получим: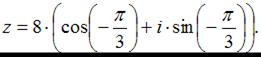 
ЗАДАНИЕ N 2
Тема: Тригонометрическая форма комплексного числа
Произведение комплексных чисел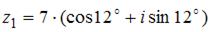 
и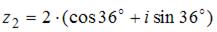 
равно …
Решение:
Воспользуемся формулой: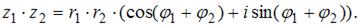 
Получим: 
ЗАДАНИЕ N 3
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа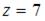 
имеет вид …
Решение:
Для представления комплексного числа в тригонометрической форме записи необходимо найти его модуль и аргумент.
Заметим, что мнимая часть данного комплексного числа равна нулю, поэтому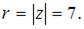 
Точка, изображающая это число, принадлежит положительной части действительной оси, значит,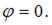 
Зная, что тригонометрическая форма комплексного числа имеет вид
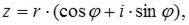получим: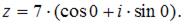 
ЗАДАНИЕ N 4
Тема: Тригонометрическая форма комплексного числа
Частное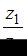 
комплексных чисел 
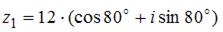и 
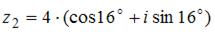равно …
Решение:
Воспользуемся формулой: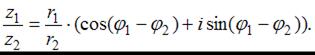 
Получим:
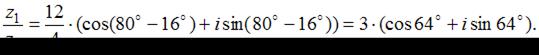
ЗАДАНИЕ N 5
Тема: Тригонометрическая форма комплексного числа
Степень комплексного числа 
равна …
Решение:
Согласно формуле Муавра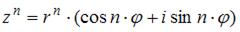 
находим:
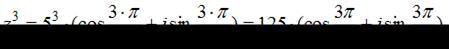
САМОСТОЯТЕЛЬНАЯ РАБОТА 18
ЗАДАНИЕ N 1
Тема: Тригонометрическая форма комплексного числа
Степень комплексного числа 
равна …
ЗАДАНИЕ N 2
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа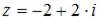 
имеет вид …
ЗАДАНИЕ N 3
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа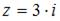 
имеет вид …
ЗАДАНИЕ N 4
Тема: Тригонометрическая форма комплексного числа
Частное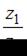 
комплексных чисел 
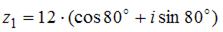и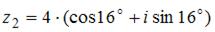 
равно …
ЗАДАНИЕ N 5
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа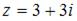 
имеет вид …
ЗАДАНИЕ N 6
Тема: Тригонометрическая форма комплексного числа
Частное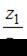 
комплексных чисел 
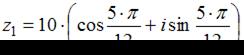и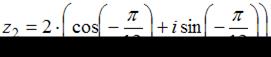 
равно …
ЗАДАНИЕ N 7
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа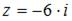 
имеет вид …
ЗАДАНИЕ N 8
Тема: Тригонометрическая форма комплексного числа
Степень комплексного числа 
равна …
ЗАДАНИЕ N 9
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа 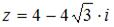имеет вид …
ЗАДАНИЕ N 10
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа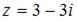 
имеет вид …
ЗАДАНИЕ N 11
Тема: Тригонометрическая форма комплексного числа
Частное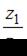 
комплексных чисел 
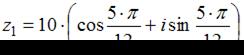и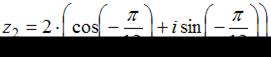 
равно …
ЗАДАНИЕ N 12
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа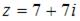 
имеет вид …
ЗАДАНИЕ N 13
Тема: Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа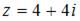 
имеет вид …
ЗАДАНИЕ N 14
Тема: Тригонометрическая форма комплексного числа
Произведение комплексных чисел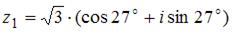 
и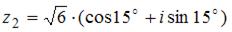 
равно …
РАЗДЕЛ 7.
ТЕМА 19 СПОСОБЫ ЗАДАНИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
КОНСПЕКТ 19
19.1 СПОСОБЫ ЗАДАНИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Наиболее часто встречаются четыре самых распространенных способа задания числовых последовательностей
- С помощью формулы общего члена последовательности
- Рекуррентный способ
- Графический способ
- Перечислением первых нескольких членов последовательности (выстроенных в ряд )
Пример 1
Вычислить пять первых членов последовательности x n=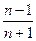 
.
Решение:
Подставив вместо n последовательно 1,2,3,4,5,получим x1=0, x2=1/3, x3=1/2, x4=3/5, x5=2/3.
Пример 2
Последовательность задана рекуррентным соотношением xn= 3xn+1.Найти первые члены последовательности.
Решение:
Зададим первый член последовательности: пусть x1=2.Полагая в рекуррентном соотношении n=2, получим x2=3x2-1+1=3x1+1=3*2+1=7.При n=3,4,5 соответственно находим: x3=3x2+1=3*7+1=22, x4=3x3+1=3*22+1=67, x5=3x4+1=3*67+1=202. В результате получаем последовательность 2, 7, 22, 67, 202, … .
Пример 3
Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 1.
Решение:
Для того чтобы число при делении на 3 давало остаток 1, оно должно иметь вид 3n+1; следовательно, общий член последовательности xn=3n+1.
19.2 ПРЕДЕЛ. ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является главной задачей.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….
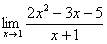
Любой предел состоит из трех частей:
1) Всем известного значка предела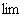 
.
2) Записи под значком предела, в данном случае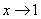 
. Запись читается «икс стремится к единице». Чаще всего – именно 
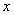, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( 
).
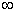3) Функции под знаком предела, в данном случае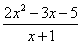 
.
Сама запись 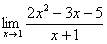читается так: «предел функции 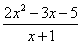при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала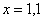 
, затем 
, 
, …, 
, ….
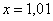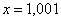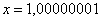То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
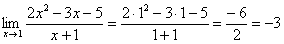
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
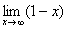
Разбираемся, что такое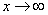 
? Это тот случай, когда 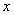неограниченно возрастает, то есть: сначала 
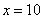, потом 
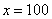, потом 
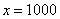, затем 
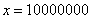и так далее до бесконечности.
А что в это время происходит с функцией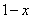 
?
, 
, 
, …
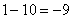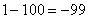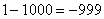Итак: если 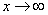, то функция 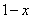стремится к минус бесконечности:
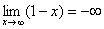
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию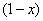 
бесконечность и получаем ответ.
Еще один пример с бесконечностью:
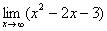
Опять начинаем увеличивать 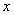до бесконечности, и смотрим на поведение функции:
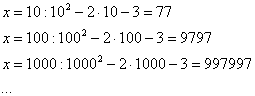
Вывод: при 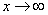функция 
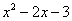неограниченно возрастает
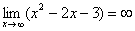
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
, 
, 
, 
, 
, 
, 
, 
, 
, 
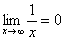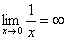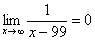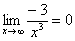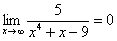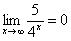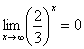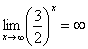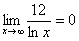
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если 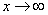, попробуйте построить последовательность 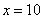, , 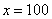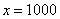. Если 
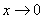, то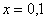 
, 
, 
.
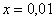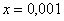Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: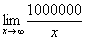 
, то все равно 
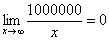, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
Дата: 2019-07-31, просмотров: 159.
