Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой функции 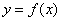 , осью
, осью 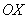 и прямыми
и прямыми 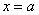 ,
, 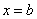 :
:
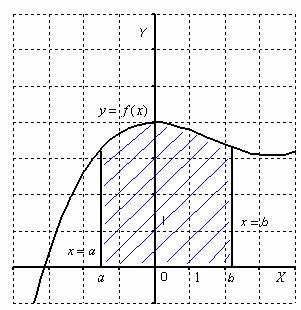
Площадь криволинейной трапеции численно равна определенному интегралу 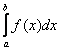 . У любого определенного интеграла (который существует) есть очень хороший геометрический смысл. С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.
. У любого определенного интеграла (который существует) есть очень хороший геометрический смысл. С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.
То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Например, рассмотрим определенный интеграл 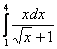 . Подынтегральная функция
. Подынтегральная функция  задает на плоскости некоторую кривую (её можно всегда при желании начертить), а сам определенный интеграл
задает на плоскости некоторую кривую (её можно всегда при желании начертить), а сам определенный интеграл 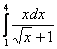 численно равен площади соответствующей криволинейной трапеции.
численно равен площади соответствующей криволинейной трапеции.
Пример 1
Вычислить площадь фигуры, ограниченной линиями 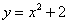 ,
, 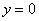 ,
, 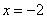 ,
, 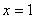 .
.
Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа. Причем, чертеж необходимо построить ПРАВИЛЬНО.
При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. Графики функций выгоднее строить поточечно. В данной задаче решение может выглядеть так.
Выполним чертеж (обратите внимание, что уравнение 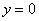 задает ось
задает ось 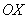 ):
):
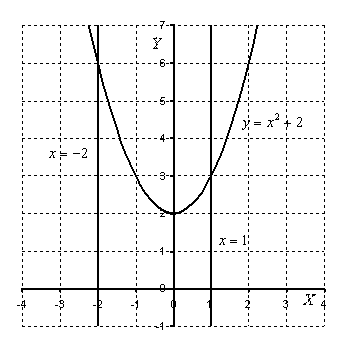
Штриховать криволинейную трапецию я не буду, здесь очевидно, о какой площади идет речь. Решение продолжается так:
На отрезке 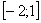 график функции
график функции 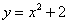 расположен над осью
расположен над осью 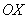 , поэтому:
, поэтому:
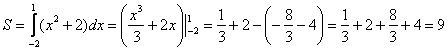
Ответ: 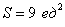
У кого возникли трудности с вычислением определенного интеграла и применением формулы Ньютона-Лейбница 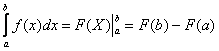 .
.
ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА
Физический смысл определенного интеграла в механике состоит в том, что путь  , пройденный телом за отрезок времени от
, пройденный телом за отрезок времени от 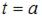 до
до 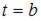 , движущимся прямолинейно со скоростью
, движущимся прямолинейно со скоростью 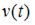 , вычисляется по формуле:
, вычисляется по формуле:
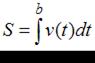 .
.
ПРАКТИКУМ 13
ЗАДАНИЕ N 1
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением 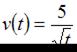 . Тогда путь, пройденный телом за 9 секунд от начала движения, равен …
. Тогда путь, пройденный телом за 9 секунд от начала движения, равен …
Решение:
Напоминаем, что путь 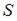 , пройденный телом за отрезок времени от
, пройденный телом за отрезок времени от 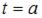 до
до 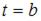 , движущимся прямолинейно со скоростью
, движущимся прямолинейно со скоростью 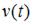 , вычисляется по формуле:
, вычисляется по формуле:
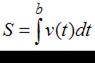 .
.
Тогда, используя условие, имеем:
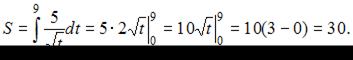
ЗАДАНИЕ N 2
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением 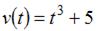 . Тогда путь, пройденный телом за 2 секунды от начала движения, равен …
. Тогда путь, пройденный телом за 2 секунды от начала движения, равен …
Решение:
Напоминаем, что путь  , пройденный телом за отрезок времени от
, пройденный телом за отрезок времени от 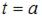 до
до 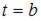 , движущимся прямолинейно со скоростью
, движущимся прямолинейно со скоростью 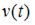 , вычисляется по формуле:
, вычисляется по формуле:
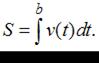
Тогда, используя условие, имеем:
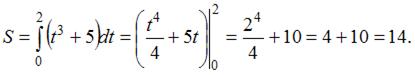
ЗАДАНИЕ N 3
Тема: Геометрические приложения определенного интеграла
Площадь фигуры, ограниченной параболой 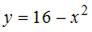 и осью ОХ, равна …
и осью ОХ, равна …
Решение:
Обращаем внимание, что площадь данной плоской фигуры вычисляется по формуле 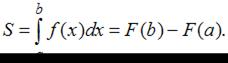
В данной задаче сначала необходимо найти пределы интегрирования (точки пересечения параболы с осью ОХ): 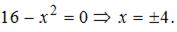
Тогда
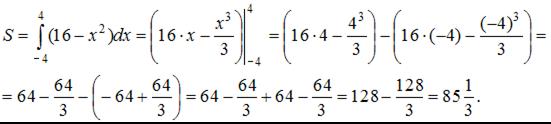
Площадь фигуры равна 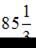 (кв. ед.).
(кв. ед.).
ЗАДАНИЕ N 4
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением  . Тогда путь, пройденный телом за время от второй секунды до шестой секунды движения, равен …
. Тогда путь, пройденный телом за время от второй секунды до шестой секунды движения, равен …
Решение:
Напоминаем, что путь  , пройденный телом за отрезок времени от
, пройденный телом за отрезок времени от 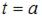 до
до 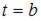 , движущимся прямолинейно со скоростью
, движущимся прямолинейно со скоростью 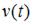 , вычисляется по формуле:
, вычисляется по формуле:
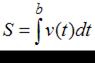 .
.
Тогда, используя условие, имеем:

ЗАДАНИЕ N 5
Тема: Геометрические приложения определенного интеграла
Площадь фигуры, ограниченной параболой 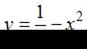 и осью ОХ, равна …
и осью ОХ, равна …
Решение:
Обращаем внимание, что площадь данной плоской фигуры вычисляется по формуле 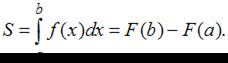
В данной задаче сначала необходимо найти пределы интегрирования (точки пересечения параболы с осью ОХ): 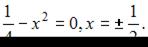
Тогда
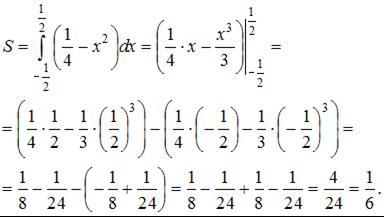
Площадь фигуры равна 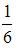 (кв. ед.).
(кв. ед.).
ЗАДАНИЕ N 6
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением  . Тогда путь, пройденный телом за 4 секунды от начала движения, равен …
. Тогда путь, пройденный телом за 4 секунды от начала движения, равен …
Решение:
Напоминаем, что путь 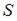 , пройденный телом за отрезок времени от
, пройденный телом за отрезок времени от 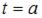 до
до 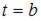 , движущимся прямолинейно со скоростью
, движущимся прямолинейно со скоростью 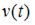 , вычисляется по формуле:
, вычисляется по формуле:
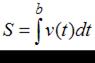 .
.
Тогда, используя условие, имеем:
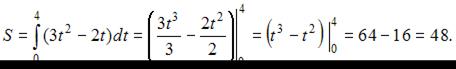
САМОСТОЯТЕЛЬНАЯ РАБОТА 13
ЗАДАНИЕ N 1
Тема: Геометрические приложения определенного интеграла
Площадь фигуры, ограниченной параболой  и осью ОХ, равна …
и осью ОХ, равна …
ЗАДАНИЕ N 2
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением 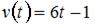 . Тогда путь, пройденный телом за время от второй секунды до четвертой секунды движения, равен …
. Тогда путь, пройденный телом за время от второй секунды до четвертой секунды движения, равен …
ЗАДАНИЕ N 3
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением 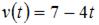 . Тогда путь, пройденный телом за 3 секунды от начала движения, равен …
. Тогда путь, пройденный телом за 3 секунды от начала движения, равен …
ЗАДАНИЕ N 4
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением 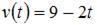 . Тогда путь, пройденный телом за 4 секунды от начала движения, равен …
. Тогда путь, пройденный телом за 4 секунды от начала движения, равен …
ЗАДАНИЕ N 5
Тема: Геометрические приложения определенного интеграла
Площадь фигуры, ограниченной параболой  и осью ОХ, равна …
и осью ОХ, равна …
ЗАДАНИЕ N 6
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением  . Тогда путь, пройденный телом за 5 секунд от начала движения, равен …
. Тогда путь, пройденный телом за 5 секунд от начала движения, равен …
ЗАДАНИЕ N 7
Тема: Физические приложения определенного интеграла
Скорость движения тела задана уравнением 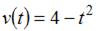 . Тогда путь, пройденный телом за 3 секунды от начала движения, равен …
. Тогда путь, пройденный телом за 3 секунды от начала движения, равен …
РАЗДЕЛ 5.
Дата: 2019-07-31, просмотров: 319.